Engage NY Eureka Math Geometry Module 2 Lesson 28 Answer Key
Eureka Math Geometry Module 2 Lesson 28 Example Answer Key
Example 1.
Find the value of a and b.
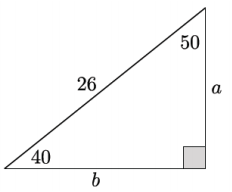
Answer:
→ Now that we can calculate the sine and cosine of a given angle using a calculator, we can use the decimal value of the ratio to determine the unknown side length of a triangle.
Consider the following triangle.
→ What can we do to find the length of side a?
We can find the sin 40 or cos 50.
→ Let’s begin by using the sin 40. We expect sin 40 = \(\frac{a}{26}\). Why?
By definition of sine; sin θ = \(\frac{\text { opp }}{\text { hyp }}\).
→ To calculate the length of a, we must determine the value of 26 sin 40 because a = 26 sin 40. We will round our answer to two decimal places.
→ Using the decimal approximation of sin 40 ≈ 0.642 8, we can write
26(0.6428) ≈ a
16.71 ≈ a
→ Now let’s use cos 50, which is approximately 0.6428. What do you expect the result to be? Explain.
I expect the result to be the same. Since the approximation of sin 40 is equal to the approximation of cos 50, the computation should be the same.
Note that students may say that sin 40 = cos 50. Ensure that students know that once decimal approximations are used in place of the functions, they are no longer looking at two quantities that are equal because the decimals are approximations. To this end, ask students to recall that in Exercise1 they were only taking the first four decimal digits of the number; that is, they are using approximations of those values. Therefore, they cannot explicitly claim that sin 40 = cos 50, rather that their approximations are extremely close in value to one another.
If necessary, show the computation below that verifies the claim made above.
cos 50 = \(\frac{a}{26}\)
26 cos 50 = a
26(0.6428) ≈ a
16.71 ≈ a
→ Now, calculate the length of side b.
Side b can be determined using sin 50 or cos 40.
26(0.7660) ≈ b
19.92 ≈ b
→ Could we have used another method to determine the length of side b?
Yes. Because this is a right triangle and two sides are known, we could use the Pythagorean theorem to determine the length of the third side.
The points below are to make clear that the calculator gives approximations of the ratios we desire when using trigonometric functions.
→ When we use a calculator to compute, what we get is a decimal approximation of the ratio \(\frac{a}{26}\). Our calculators are programmed to know which number a is needed, relative to 26, so that the value of the ratio \(\frac{a}{26}\) is equal to the value of sin 40. For example, sin 40 = \(\frac{a}{26}\) and sin 40 ≈ 0.6428. Our calculators give us the number a that, when divided by 26, is closest to the actual value of sin 40.
→ Here is a simpler example illustrating this fact. Consider a right triangle with an acute angle of 300 and hypotenuse length of 9 units. Then, sin 30 = \(\frac{a}{9}\). We know that sin 30 = \(\frac{1}{2}\) = 0.5. What our calculators do is find the number a so that \(\frac{a}{9}=\frac{1}{2}\) = 0.5, which is a = 4.5.
Example 2.
Johanna borrowed some tools from a friend so that she could precisely, but not exactly, measure the corner space in her backyard to plant some vegetables. She wants to build a fence to prevent her dog from digging up the seeds that she plants. Johanna returned the tools to her friend before making the most Important measurement: the one that would give the length of the fence!
Johanna decided that she could just use the Pythagorean theorem to find the length of the fence she would need. Is the Pythagorean theorem applicable in this situation? Explain.
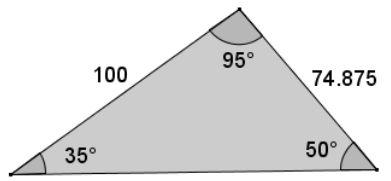
Answer:
No The corner of her backyard is not a 90° angle; therefore, the Pythagorean theorem cannot be applied in this situation. The Pythagorean theorem will, however, provide an approximation since the given angle has a measure that is close to 90°.
→ What can we do to help Johanna figure out the length of fence she needs?
I Provide time for students to discuss this in pairs or small groups. Allow them to make sense of the problem and persevere in solving it. It may be necessary to guide their thinking using the prompts below.
→ If we dropped an altitude from the angle with measure 950, could that help? How?
→ Would we be able to use the Pythagorean theorem now? Explain.
→ If we denote the side opposite the 95° angle as x and y, as shown, can we use what we know about sine and cosine? Explain.
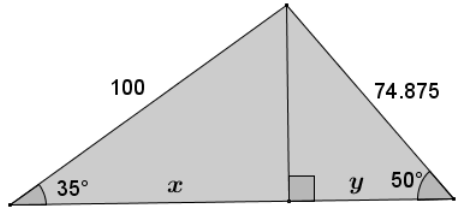
The missing side length is equal to x + y. The length x is equal to 100 cos 35, and the length y is equal to 74.875 cos 50. Therefore, the length of
x + y = 100 cos 35 + 74.875 cos 50 ≈ 81.92 + 48.12872 130.05.
Note: The Pythagorean theorem provides a reasonable approximation of 124.93.
Eureka Math Geometry Module 2 Lesson 28 Exercise Answer Key
Exercise 1.
a. The bus drops you off at the corner of H Street and 1st Street, approximately 300 ft. from school. You plan to walk to your friend Janneth’s house after school to work on a project. Approximately how many feet will you have to walk from school to Janneth’s house? Round your answer to the nearest foot. (Hint: Use the ratios you developed in Lesson 25.)
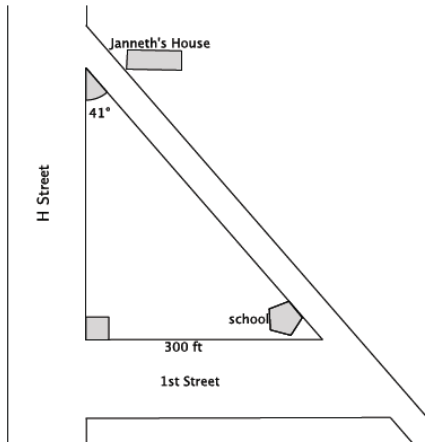
Answer:
Let x represent the distance from school to Janneth’s house.
sin θ = \(\frac{\text { opp }}{\text { hyp }}\), then sin 41 = \(\frac{5.3}{8}\). Then, \(\frac{300}{x}\) = \(\frac{5.3}{8}\) and
x = 452.8301887…
The distance I will have to walk from school to Janneth’s house is approximately 453 ft.
b. In real life, it is unlikely that you would calculate the distance between school and Janneth’s house in this manner. Describe a similar situation in which you might actually want to determine the distance between two points using a trigonometric ratio.
Answer:
Accept any reasonable responses. Some may include needing to calculate the distance to determine if a vehicle has enough fuel to make the trip or the need to determine the length prior to attempting the walk because a friend is on crutches and cannot easily get from one location to the next when the distance is too long.
Exercise 2.
Use a calculator to find the sine and cosine of θ. Give your answer rounded to the ten-thousandth place.

Answer:

Exercise 3.
What do you notice about the numbers in the row sin θ compared with the numbers in the row cos θ?
Answer:
The numbers are the same but reversed in order.
Exercise 4.
Provide an explanation for what you noticed in Exercise 2.
Answer:
The pattern exists because the sine and cosine of complementary angles are equal.
Exercise 5.
A shipmate set a boat to sail exactly 27° NE from the dock. After traveling 120 miles, the shipmate realized he had misunderstood the instructions from the captain; he was supposed to set sail going directly east!
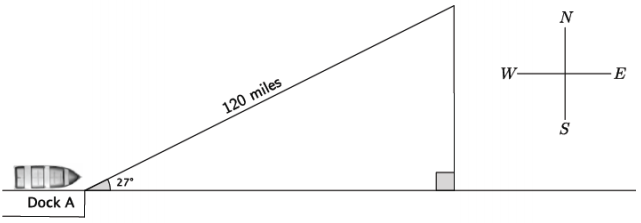
a. How many miles will the shipmate have to travel directly south before he is directly east of the dock? Round your answer to the nearest mile.
Answer:
Let S represent the distance they traveled directly south.
sin 27 = \(\frac{S}{120}\)
120 sin 27 = S
54.47885997… = S
He traveled approximately 54 mi. south.
b. How many extra miles does the shipmate travel by going the wrong direction compared to going directly east? Round your answer to the nearest mile.
Answer:
Solutions may vary. Some students may use the Pythagorean theorem while others may use the cosine function. Both are acceptable strategies. If students use different strategies, make sure to share them with the class, and discuss the benefits of each.
Let E represent the distance the boat is when it is directly east of the dock.
cos 27 = \(\frac{E}{120}\)
120 cos 27 = E
106.9207829… = E
107 ≈ E
The total distance traveled by the boat is 120 + 54 = 174. They ended up exactly 107 miles east of the dock. 174 – 107 = 67,so they traveled an extra 67 miles.
Exercise 6.
The measurements of the triangle shown below are rounded to the nearest hundredth. Calculate the missing side length to the nearest hundredth.
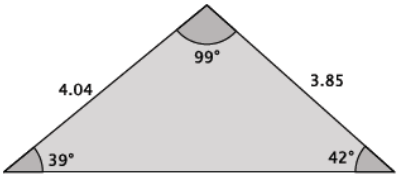
Answer:
Drop an altitude from the angle that measures 99°.
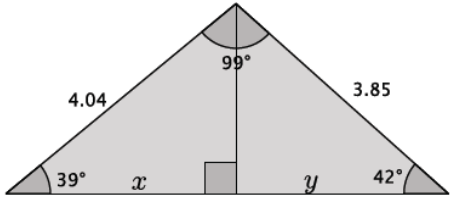
Then, the length of the missing side is x + y, which can be found by
4.04 cos 39 + 3.85 cos 42 ≈ 3.139669 + 2.861107 = 6.000776 ≈ 6.00.
Eureka Math Geometry Module 2 Lesson 28 Problem Set Answer Key
Question 1.
Given right triangle GHI, with right angle at H, GH = 12. 2, and m∠G = 28°, find the measures of the remaining sides and angle to the nearest tenth.
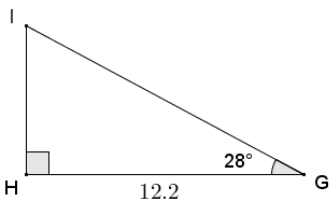
Answer:
cos 28 = \(\frac{12.2}{G I}\)
GI = \(\frac{12.2}{\cos 28}\)
GI ≈ 13.8
tan 28 = \(\frac{\text { IH }}{12.2}\)
IH = 12.2 tan 28
IH ≈ 6.5
28° + m∠I = 90°
m∠I = 62°
Question 2.
The Occupational Safety and Health Administration (OSHA) provides standards for safety at the workplace. A ladder is leaned against a vertical wall according to OSHA standards and forms an angle of approximately 75° with the floor.
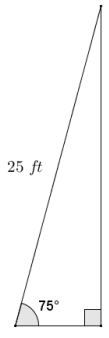
a. If the ladder is 25 ft. long, what is the distance from the base of the ladder to the base of the wall?
Answer:
Let b represent the distance of the base of the ladder from the wall in feet.
b = 25(cos 75)
b ≈ 6.5
The base of the ladder is approximately 6 ft. 6 in. from the wall.
b. How high on the wall does the ladder make contact?
Answer:
Let h represent the height on the wall where the ladder makes contact in feet.
h = 25(sin75)
h ≈ 24.1
The ladder contacts the wall just over 24 ft. above the ground.
c. Describe how to safely set a ladder according to OSHA standards without using a protractor.
Answer:
Answers will vary. Possible description:
The horizontal distance of the base of the ladder to the point of contact of the ladder should be approximately \(\frac{1}{4}\) of the length of the ladder.
Question 3.
A regular pentagon with side lengths of 14 cm is inscribed in a circle. What is the radius of the circle?
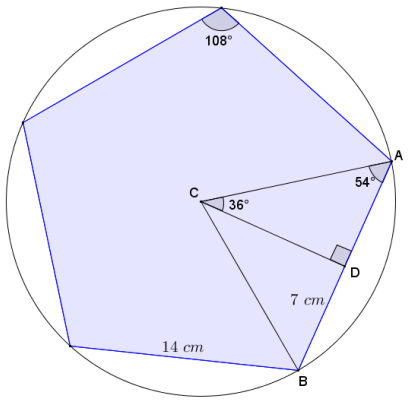
Answer:
Draw radii from center C of the circle to two consecutive vertices of the pentagon, A and B, and draw an altitude from the center C to D on \(\overline{A B}\).
The interior angles of a regular pentagon have measure of 108°, and \(\overline{A C}\) and \(\overline{B C}\) bisect the interior angles at A and B.
AD = BD = 7 cm
Let x represent the lengths of \(\overline{A C}\) in centimeters.
Using cosine, cos 54 = \(\frac{7}{x}\) and thus:
x = \(\frac{7}{\cos 54}\)
x ≈ 11.9.
\(\overline{A C}\) is a radius of the circle and has a length of approximately 11.9 cm.
Question 4.
The circular frame of a Ferris wheel is suspended so that it sits 4 ft. above the ground and has a radius of 30 ft. A segment joins center C to point S on the circle. If \(\overline{C S}\) makes an angle of 48° with the horizon, what is the distance of point S to the ground?
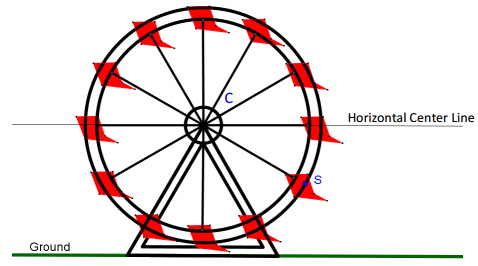
Answer:
Note to teacher: There are two correct answers to this problem since the segment can make an angle of 48° above or below the horizon in four distinct locations, providing two different heights above the ground.
There are four locations at which the segment makes an angle of 48° with the horizon. In each case, \(\overline{C S}\) is the hypotenuse of a right triangle with acute angles with measures of 48° and 42°.
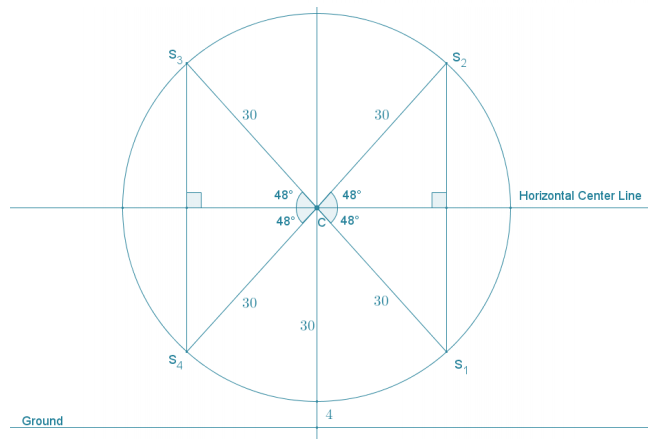
Let d represent the distance in feet from point S to the horizon (applies to each case):
sin 48 = \(\frac{d}{30}\)
30 (sin 48) = d
22.3 ≈ d
The center of the Ferris wheel is 34 ft. above the ground; therefore, the distance from points S1 and S4 to the ground in feet is
34 – 22.3 = 11.7.
Points S2 and S3 are approximately 22.3 ft. above the center of the Ferris wheel, so the distance from S2 and S3 to the ground in feet is
34 + 22.3 = 56.3.
When \(\overline{C S}\) forms a 48° angle with the horizon, point S is either approximately 11.7 ft. above the ground or approximately 56.3 ft. above the ground.
Question 5.
Tim is a contractor who is designing a wheelchair ramp for handicapped access to a business. According to the Americans with Disabilities Act (ADA), the maximum slope allowed for a public wheelchair ramp forms an angle of approximately 4. 76° to level ground. The length of a ramp’s surface cannot exceed 30 ft. without including a flat 5 ft. × 5 ft. platform (minimum dimensions) on which a person can rest, and such a platform must be included at the bottom and top of any ramp.
Tim designs a ramp that forms an angle of 4° to the level ground to reach the entrance of the building. The entrance of the building is 2 ft. 9 in. above the ground. Let x and y as shown in Tim’s initial design below be the indicated distances in feet.
a. Assuming that the ground in front of the building’s entrance is flat, use Tim’s measurements and the ADA requirements to complete and/or revise his wheelchair ramp design.

Answer:
Note to teacher: Student designs will vary; however, the length of the ramp’s surface is greater than 30 ft., which requires at least one resting platform along the ramp. Furthermore, Tim’s design does not include a platform at the top of the ramp as required by the guidelines, rendering his design incorrect.
Possible student solution:
2 ft. 9 in. = 2.75ft.
Using tangent, tan 4 = \(\frac{2.75}{x}\), and thus
x = \(\frac{2.75}{\tan 4}\)
x ≈ 39.33.
The ramp begins approximately 39 ft. 4 in. from the building; thus, the in length. The hypotenuse of the triangle represents the sloped surface the legs. Tim’s design will not meet the ADA guidelines because it does the ramp’s slope, nor does it include a platform at the top of the ramp. ground. The student’s design may or may not include a platform at the ramp’s surface is greater than 30 ft. of the ramp and must be longer than not include a flat resting section along (The bottom of the ramp is flat bottom.)
The vertical distance from the ground to the entrance is 2.75 ft. Using sine, sin 4 = \(\frac{2.75}{y}\), and thus,
y = \(\frac{2.75}{\sin 4}\)
y ≈ 39.42.
The total length of the ramp surface is approximately 39 ft. 5 in.; however, because of its length, it requires a resting platform somewhere in the first 30 ft. and another platform at the top.
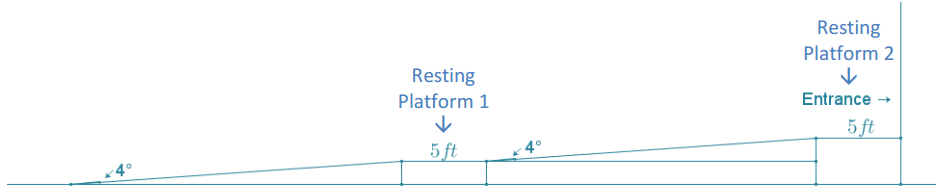
b. What is the total distance from the start of the ramp to the entrance of the building in your design?
Answer:
If each platform is 5 ft. in length, then the total distance along the ramp from the ground to the building is approximately 49 ft. 5 in.
Question 6.
Tim is designing a roof truss in the shape of an isosceles triangle. The design shows the base angles of the truss to have measures of 18. 5°. If the horizontal base of the roof truss is 36 ft. across, what is the height of the truss?
Answer:
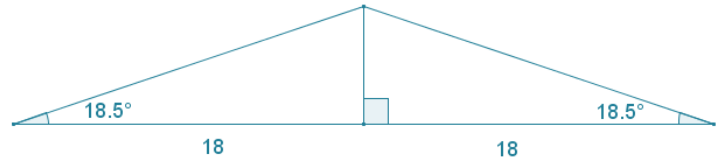
Let h represent the height of the truss in feet. Using tangent, tan 18.5 = \(\frac{h}{18}\), and thus,
h = 18(tan 18. 5)
h ≈ 6.
The height of the truss is approximately 6 ft.
Eureka Math Geometry Module 2 Lesson 28 Exit Ticket Answer Key
Question 1.
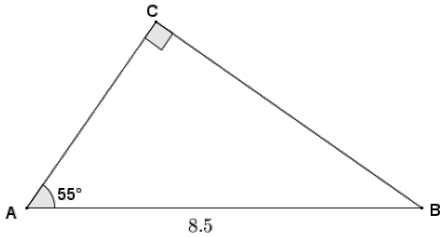
Given right triangle ABC with hypotenuse AB = 8.5 and m∠A = 55°, find AC and BC to the nearest hundredth.
Answer:
BC = 8. 5(sin 55)
BC ≈ 6.96
AC = 8.5 (cos 55)
AC ≈ 4.88
Question 2.
Given triangle DEF, m∠D = 22°, m∠F = 91°, DF = 16. 55, and EF = 6.74, find DE to the nearest hundredth.
Answer:
Draw altitude from F to \(\overline{D E}\) at point P. Cosines can be used on angles D and E to determine the lengths of \(\overline{D P}\) and \(\overline{P E}\), which together compose \(\overline{D E}\).
PE = 6. 74(cos 67)
PE ≈ 2. 6335
DP = 16. 55(cos 22)
DP ≈ 15. 3449
DE = DP+PE
DE ≈ 15. 3449 + 2. 6335
DE ≈ 17.98
Note to teacher: Answers of DE ≈ 17.97 result from rounding to the nearest hundredth too early in the problem.