Engage NY Eureka Math Geometry Module 2 Lesson 16 Answer Key
Eureka Math Geometry Module 2 Lesson 16 Example Answer Key
Example 1.
Given ∆ ABC ~ ∆ A’B’C’, find the missing side lengths.
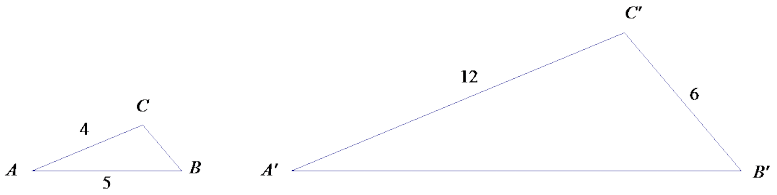
Answer:
→ (Take a poll.) How many people used the ratio of lengths 4: 12 or 12: 4 (i.e., the corresponding lengths of \(\overline{A C}\) and \(\overline{A^{\prime} C^{\prime}}\)) to determine the measurements of \(\overline{B C}\) and \(\overline{A^{\prime} B^{\prime}}\)?
→ Are there any other length relationships we could use to set up an equation and solve for the missing side lengths?
Provide students time to think about and try different equations that would lead to the same answer.
In addition to the ratio of corresponding lengths AC: A’C’, we can use a ratio of lengths within one of the triangles. For example, we could use the ratio of AC: AB to find the length of \(\overline{A^{\prime} B^{\prime}}\). Equating the values of the ratios, we get the following:
\(\frac{4}{5}=\frac{12}{A^{\prime} B^{\prime}}\)
A’B’ = 15.
To find the length of \(\overline{B C}\), we can use the ratios A’ C’: B’ C’ and AC: BC. Equating the values of the ratios, we get the following:
→ Why is it possible to use this length relationship, AC: AB, to solve for a missing side length?
Take student responses, and then offer the following explanation:
→ There are three methods that we can use to determine the missing side lengths.
Method 1 (Scale Factor): Find the scale factor, and use it to compute for the desired side lengths.
Since we know AC = 4 and the corresponding side A’C’ = 12, the scale factor of r satisfies 4r = 12. So,
r = 3, A’B’ = rAB = 3 · 5 = 15, and BC \(\frac{6}{3}\) = 2.
Method 2 (Ratios Between-Figures): Equate the values of the ratios of the corresponding sides.
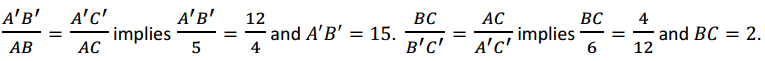
Method 3 (Ratios Within-Figures): Equate the values of the ratios within each triangle.
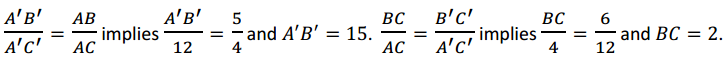
→ Why does Method 3 work? That is, why can we use values of ratios within each triangle to find the missing side lengths?
Provide students time to explain why Method 3 works, and then offer the following explanation:
→ If ∆, ABC ~ ∆ A’B’C’, then it is true that the ratio between any two side lengths of the first triangle is equal to the ratio between the corresponding side lengths of the second triangle; for example, AB: BC = A’B’: B’C’. This is because if r is the scale factor, then AB: BC = rAB: rBC = A’B’: B’C’.
Revisit the Opening Exercise. Ask students to explain which method they used to write their equations for the height of the tree. Answers may vary, but students likely have used Method 2 because that is what is most familiar to them.
Example 2.
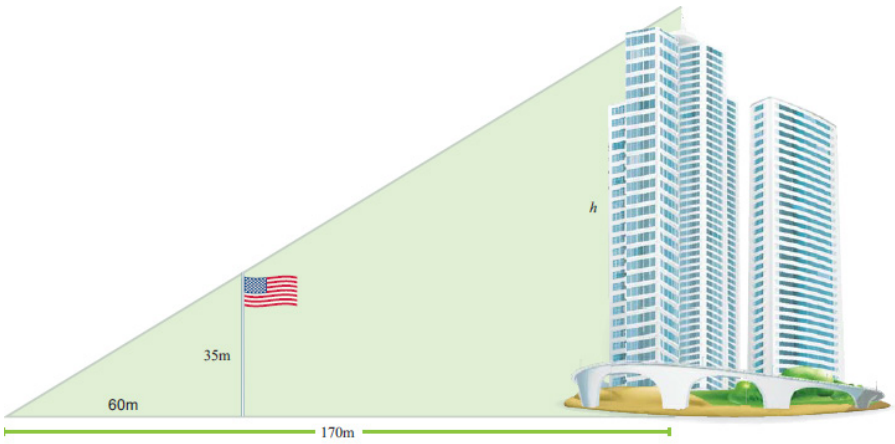
In the diagram above, a large flagpole stands outside of an office building. Marquis realizes that when he looks up from the ground 60 m away from the flagpole, the top of the flagpole and the top of the building line up. If the flagpole is 35 m tall and Marquis is 170 m from the building, how tall is the building?
a. Are the triangles in the diagram similar? Explain.
Answer:
Yes, the triangle formed by Marquis, the ground, and the flagpole is similar to the triangle formed by Marquis, the ground, and the building. They are similar by the AA criterion. Each of the triangles has a common angle with Marquis at the vertex, and each triangle has a right angle, where the flagpole and the building meet the ground.
b. Determine the height of the building using what you know about scale factors.
Answer:
The scale factor is \(\frac{170}{60}=\frac{17}{6}=2.8 \overline{3}\). Then, the height of the building is 35(2. 8\(\overline{3}\)) = 99.1\(\overline{6}\) m.
c. Determine the height of the building using ratios between similar figures.
Answer:
\(\frac{35}{h}=\frac{60}{170}\)
5950 = 60h
h = 99.1
d. Determine the height of the building using ratios within similar figures.
Answer:
\(\frac{35}{60}=\frac{h}{170}\)
5950 = 60h
h = 991g
Example 3
The following right triangles are similar. We will determine the unknown side lengths by using ratios within the first triangle. For each of the triangles below, we define the base as the horizontal length of the triangle and the height as the vertical length.
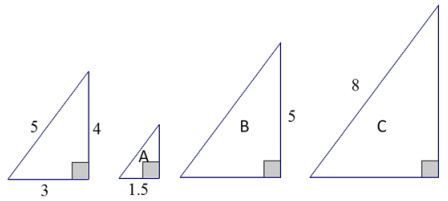
a. Write and find the value of the ratio that compares the height to the hypotenuse of the leftmost triangle.
Answer:
\(\frac{4}{5}\) = 0.8
b. Write and find the value of the ratio that compares the base to the hypotenuse of the leftmost triangle.
Answer:
\(\frac{3}{5}\) = 0.6
c. Write and find the value of the ratio that compares the height to the base of the leftmost triangle.
Answer:
\(\frac{4}{3}=1 . \overline{3}\)
d. Use the triangle with lengths 3 – 4 – 5 and triangle A to answer the following questions:
i. Which ratio can be used to determine the height of triangle A?
Answer:
The ratio that compares the height to the base can be used to determine the height of triangle A.
ii. Which ratio can be used to determine the hypotenuse of triangle A?
Answer:
The ratio that compares the base to the hypotenuse can be used to determine the hypotenuse of triangle A.
iii. Find the unknown lengths of triangle A.
Answer:
Let h represent the height of the triangle; then
\(\frac{h}{1.5}=1 . \overline{3}\)
h = 2.
Let c represent the length of the hypotenuse; then
\(\frac{1.5}{c}\) = 0.6
c = 2.5.
e. Use the triangle with lengths 3 – 4 – 5 and triangle B to answer the following questions:
i. Which ratio can be used to determine the base of triangle B?
Answer:
The ratio that compares the height to the base can be used to determine the base of triangle B.
ii. Which ratio can be used to determine the hypotenuse of triangle B?
Answer:
The ratio that compares the height to the hypotenuse can be used to determine the hypotenuse of triangle B.
iii. Find the unknown lengths of triangle B.
Answer:
Let b represent the length of the base; then
\(\frac{5}{b}=1 \frac{1}{3}\)
b = 3.75.
Let c represent the length of the hypotenuse; then
\(\frac{5}{c}\) = 0.8
c = 6.25.
f. Use the triangle with lengths 3-4- 5 and triangle C to answer the following questions:
i. Which ratio can be used to determine the height of triangle C?
Answer:
The ratio that compares the height to the hypotenuse can be used to determine the height of triangle C.
ii. Which ratio can be used to determine the base of triangle C?
Answer:
The ratio that compares the base to the hypotenuse can be used to determine the base of triangle C.
iii. Find the unknown lengths of triangle C.
Answer:
Let h represent the height of the triangle; then
\(\frac{h}{8}\) = 0.8
h = 6.4.
Let b represent the length of the base; then
\(\frac{b}{8}\) = 0.6
b = 4.8.
g. Explain the relationship of the ratio of the corresponding sides within a figure to the ratio of corresponding sides within a similar figure.
Answer:
Corresponding lengths of similar figures have proportional lengths, but the ratio of two lengths within a figure is equal to the corresponding ratio of two lengths in a similar figure.
h. How does the relationship you noted in part (g) allow you to determine the length of an unknown side of a triangle?
Answer:
This relationship allows us to find the length of an unknown side of a triangle. We can write the ratio of corresponding sides within the figure that contains the unknown side length. This ratio will be equal to the value of the ratio of corresponding sides where the lengths are known. Since the ratios are equal, the unknown length can be found by solving a simple equation.
Eureka Math Geometry Module 2 Lesson 16 Opening Exercise Answer Key
At a certain time of day, a 12 m flagpole casts an 8 m shadow. Write an equation that would allow you to find the height, h, of the tree that uses the length, s, of the tree’s shadow.
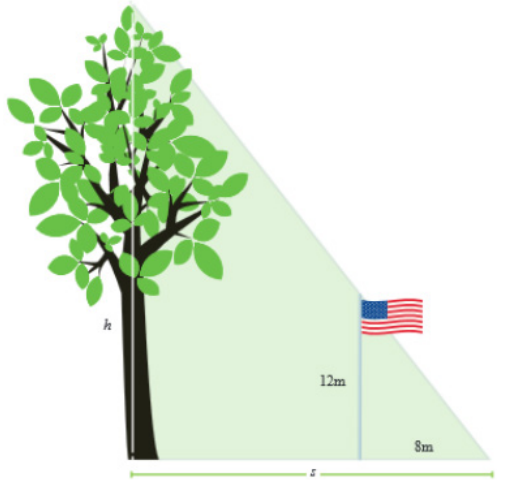
Answer:

Eureka Math Geometry Module 2 Lesson 16 Problem Set Answer Key
Question 1.
∆ DEF ~ ∆ ABC All side length measurements are in centimeters. Use between-figure ratios and/or within-figure ratios to determine the unknown side lengths.
Answer:
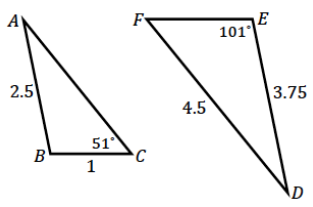
Using the given similarity statement, ∠D corresponds with ∠A, and
∠C corresponds with ∠F, so it follows that \(\overline{A B}\) corresponds with \(\overline{D E}\), \(\overline{A C}\) with \(\overline{D F}\), and \(\overline{B C}\) with \(\overline{E F}\).

Question 2.
Given ∆ ABC ∆ XYZ, answer the following questions:
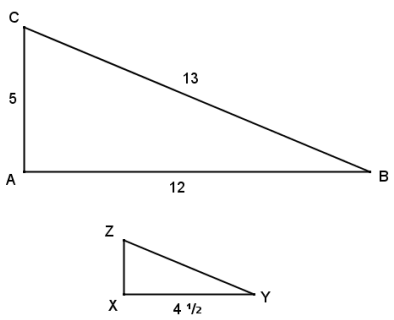
a. Write and find the value of the ratio that compares the height \(\overline{A C}\) to the hypotenuse of ∆ ABC.
Answer:
\(\frac{5}{13}\)
b. Write and find the value of the ratio that compares the base \(\overline{A B}\) to the hypotenuse of ∆ ABC.
Answer:
\(\frac{12}{13}\)
c. Write and find the value of the ratio that compares the height AC to the base AB of ∆ ABC.
Answer:
\(\frac{5}{12}\)
d. Use within-figure ratios to find the corresponding height of ∆ XYZ.
Answer:
\(\frac{5}{12}=\frac{X Z}{4.5}\)
XZ = 1\(\frac{7}{8}\)
e. Use within-figure ratios to find the hypotenuse of ∆ XYZ.
Answer:
\(\frac{12}{13}=\frac{4.5}{Y Z}\)
YZ = 4\(\frac{7}{8}\)
Question 3.
Right triangles A, B, C, and D are similar. Determine the unknown side lengths of each triangle by using ratios of side lengths within triangle A.
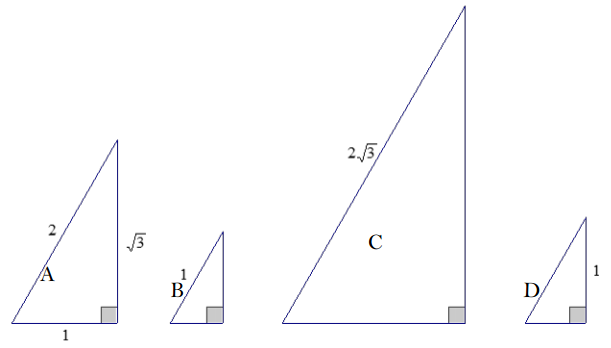
a. Write and find the value of the ratio that compares the height to the hypotenuse of triangle A.
Answer:
\(\frac{\sqrt{3}}{2}\) ≈ 0.866
b. Write and find the value of the ratio that compares the base to the hypotenuse of triangle A.
Answer:
\(\frac{1}{2}\) = 0.5
c. Write and find the value of the ratio that compares the height to the base of triangle A.
Answer:
\(\frac{\sqrt{3}}{1}\) = √3 ≈ 1.73
d. Which ratio can be used to determine the height of triangle B? Find the height of triangle B.
Answer:
The ratio that compares the height to the hypotenuse of triangle A can be used to determine the height of triangle B. Let the unknown height of triangle B be m.
\(\frac{\sqrt{3}}{2}=\frac{m}{1}\)
m = \(\frac{\sqrt{3}}{2}\)
e. Which ratio can be used to determine the base of triangle B? Find the base of triangle B.
Answer:
The ratio that compares the base to the hypotenuse of triangle A can be used to determine the base of triangle B. Let the unknown base of triangle B be n.
\(\frac{1}{2}=\frac{n}{1}\)
n = \(\frac{1}{2}\)
f. Find the unknown lengths of triangle C.
Answer:
The base of triangle C is √3.
The height of triangle C is 3.
g. Find the unknown lengths of triangle D.
Answer:
The base of triangle D is \(\frac{\sqrt{3}}{3}\).
The hypotenuse of triangle D is \(\frac{2 \sqrt{3}}{3}\).
h. Triangle E Is also similar to triangles A, B, C, and D. Find the lengths of the missing sides in terms of x.
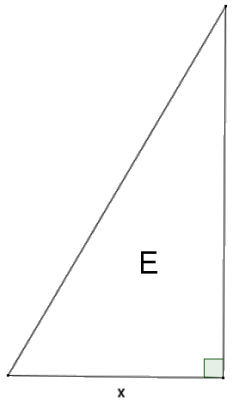
Answer:
The base of triangle E is x.
The height of triangle E is x√3.
The hypotenuse of triangle E is 2x.
Question 4.
Brian is photographing the Washington Monument and wonders how tall the monument is. Brian places his 5 ft. camera tripod approximately 100 yd. from the base of the monument. Lying on the ground, he visually aligns the top of his tripod with the top of the monument and marks his location on the ground approximately 2 ft. 9 in. from the center of his tripod. Use Brian’s measurements to approximate the height of the Washington Monument.
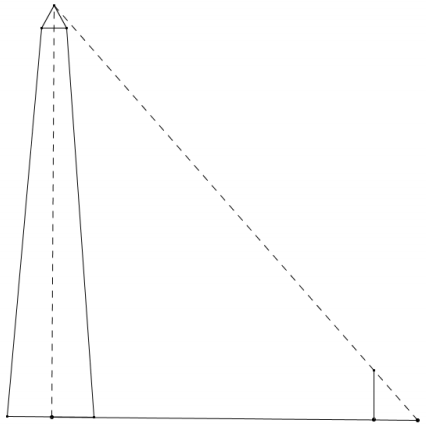
Answer:
Brian’s location on the ground is approximately 302.75 ft. from the base of the monument. His visual line forms two similar right triangles with the height of the monument and the height of his camera tripod.
\(\frac{5}{2.75}=\frac{h}{302.75}\)
1513.75 = 2.75h
550.5 ≈ h
According to Brian’s measurements, the height of the Washington Monument is approximately 550.5 ft.
Students may want to check the accuracy of this problem. The actual height of the Washington Monument is 555 ft.
Question 5.
Catarina’s boat has come untied and floated away on the lake. She ¡s standing atop a cliff that Is 35 ft. above the water in a lake. If she stands 10 ft. from the edge of the cliff, she can visually align the top of the cliff with the water at the back of her boat. Her eye level is 5\(\frac{1}{2}\) ft. above the ground. Approximately how far out from the cliff is Catarina’s boat?
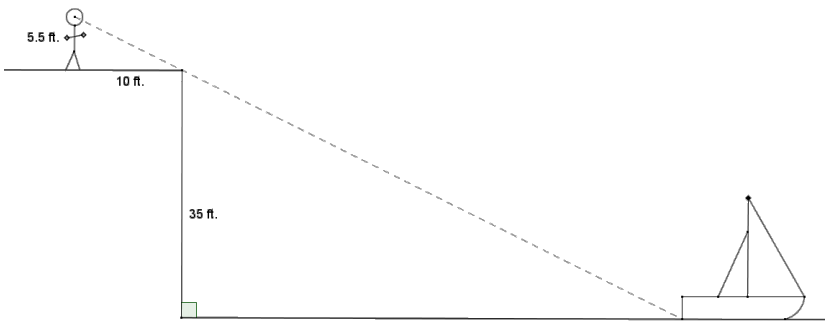
Catarina’s height and the height of the cliff both are measured perpendicularly to the ground (and water), so both triangles formed by her visual path are right triangles. Assuming that the ground level on the cliff and the water are parallel, Catarina’s visual path forms the same angle with the cliff as ¡t does with the surface of the water (corresponding ∠‘s, parallel lines). So, the right triangles are similar triangles by the AA criterion for showing triangle similarity, which means that the ratios within triangles will be equal. Let d represent the distance from the boat to the cliff:
\(\frac{5.5}{10}=\frac{35}{d}\)
5.5d = 350
d ≈ 63.6
Answer:
Catarina’s boat Is approximately 63.6 ft. away from the cliff.
Question 6.
Given the diagram below and ∆ ABC ~ ∆ XYZ, find the unknown lengths x, 2x, and 3x.
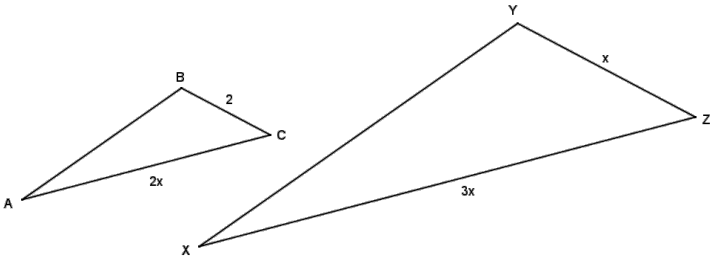
Answer:
The triangles are given as similar, so the values of the ratios of the sides within each triangle must be equal.
\(\frac{2}{2 x}=\frac{x}{3 x}\)
The sides of the larger triangle are unknown; however, the lengths include the same factor x, which is clearly nonzero, so the ratio of the sides must then be \(\frac{1}{3}\). Similarly, the sides of the smaller triangle have the same factor 2, so the value of the ratio can be rewritten as \(\frac{1}{x}\).
\(\frac{1}{x}=\frac{1}{3}\)
x = 3
Since the value of x is 3, it follows that YZ = 3, AC = 6, and XZ = 9.
Eureka Math Geometry Module 2 Lesson 16 Exit Ticket Answer Key
Question 1.
In the diagram, ∆ ABC ~ ∆ DEF by the dilation with center O and a scale factor of r. Explain why ∆ DEF ~ ∆ ABC.
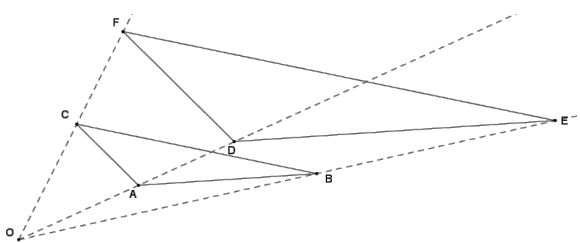
Answer:
We know that ∆ ABC ~ ∆ DEF by a dilation with center O and a scale factor of r. A dilation with the same center O but a scale factor of \(\frac{1}{r}\) maps ∆ DEF onto ∆ ABC; this means ∆ DEF ~ ∆ ABC.
Question 2.
Radii \(\overline{C A}\) and \(\overline{T S}\) are parallel. Is circle CC,CA similar to circle CT,TS? Explain.
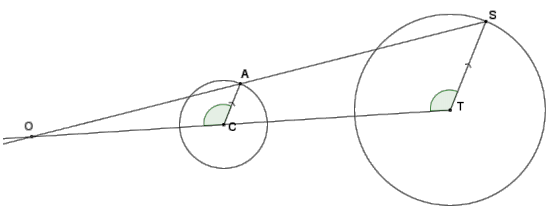
Answer:
Yes, the circles are similar because a dilation with center O and
a scale factor of r exists that maps CC,CA onto CT,TS.
Question 3.
Two triangles, ∆ ABC and ∆ DEF, are in the plane so that m∠A = m∠D, m∠B = m∠E, m∠C = m∠F, and \(\frac{D E}{A B}=\frac{E F}{B C}=\frac{D F}{A C}\) Summarize the argument that proves that the triangles must be similar.
Answer:
A dilation exists such that the lengths of one triangle can be made equal to the lengths of the other triangle. Once the triangles have lengths and angles of equal measurement, or are congruent, then a sequence of rigid motions maps one triangle to the other. Therefore, a similarity transformation exists that maps one triangle onto the other, and the triangles must be similar.