Eureka Math Geometry Module 1 Lesson 28 Answer Key

Engage NY Eureka Math Geometry Module 1 Lesson 28 Answer Key

Eureka Math Geometry Module 1 Lesson 28 Example Answer Key

Example 1.
If a quadrilateral is a parallelogram, then its opposite sides and angles are equal in measure. Complete the diagram, and develop an appropriate Given and Prove for this case. Use triangle congruence criteria to demonstrate why opposite sides and angles of a parallelogram are congruent.

Given: ____
Answer:
Parallelogram ABCD (\(\overline{A B}\) || \(\overline{C D}\), \(\overline{A D}\) || \(\overline{C B}\))
Prove: _____________
Answer:
AD=CB, AB=CD, m∠A=m∠C, m∠B=m∠D
Construction: Label the quadrilateral ABCD, and mark opposite sides as parallel. Draw diagonal \(\overline{B D}\).

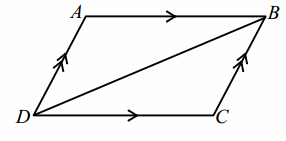
PROOF:
Parallelogram ABCD Given
m∠ABD=m∠CDB If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
BD=DB Reflexive property
m∠CBD=m∠ADB If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
△ABD≅△CDB ASA
AD=CB, AB=CD Corresponding sides of congruent triangles are equal in length.
m∠A=m∠C Corresponding angles of congruent triangles are equal in measure.
m∠ABD+m∠CBD=m∠ABC,
m∠CDB+m∠ADB=m∠ADC Angle addition postulate
m∠ABD+m∠CBD=m∠CDB+m∠ADB Addition property of equality
m∠B=m∠D Substitution property of equality

Example 2.
If a quadrilateral is a parallelogram, then the diagonals bisect each other. Complete the diagram, and develop an appropriate Given and Prove for this case. Use triangle congruence criteria to demonstrate why diagonals of a parallelogram bisect each other. Remember, now that we have proved opposite sides and angles of a parallelogram to be congruent, we are free to use these facts as needed (i.e., AD=CB, AB=CD, ∠A≅∠C, ∠B≅∠D).

Given: _____________
Answer:
Parallelogram ABCD
Prove: _______
Answer:
Diagonals bisect each other, AE=CE,DE=BE

Construction: Label the quadrilateral ABCD. Mark opposite sides as parallel. Draw diagonals \(\overline{A C}\) and \(\overline{B D}\).

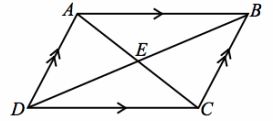
PROOF:
Parallelogram ABCD Given
m∠BAC=m∠DCA If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
m∠AEB=m∠CED Vertical angles are equal in measure.
AB=CD Opposite sides of a parallelogram are equal in length.
△AEB≅ △CED AAS
AE=CE, DE=BE Corresponding sides of congruent triangles are equal in length.

Now we have established why the properties of parallelograms that we have assumed to be true are in fact true. By extension, these facts hold for any type of parallelogram, including rectangles, squares, and rhombuses. Let us look at one last fact concerning rectangles. We established that the diagonals of general parallelograms bisect each other. Let us now demonstrate that a rectangle has congruent diagonals.

Students may need a reminder that a rectangle is a parallelogram with four right angles.

Example 3.
If the parallelogram is a rectangle, then the diagonals are equal in length. Complete the diagram, and develop an appropriate Given and Prove for this case. Use triangle congruence criteria to demonstrate why diagonals of a rectangle are congruent. As in the last proof, remember to use any already proven facts as needed.

Given: _______
Answer:
Rectangle GHIJ
Prove: _______
Answer:
Diagonals are equal in length, GI=HJ
Construction: Label the rectangle GHIJ. Mark opposite sides as parallel, and add small squares at the vertices to indicate 90° angles. Draw diagonals \(\overline{G I}\) and \(\overline{H J}\).

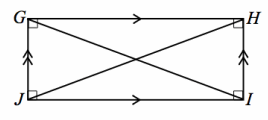
PROOF:
Rectangle GHIJ Given
GJ=IH Opposite sides of a parallelogram are equal in length.
GH=HG Reflexive property
∠JGH, ∠IHG are right angles. Definition of a rectangle
△GHJ≅ △HGI SAS
GI=HJ Corresponding sides of congruent triangles are equal in length.

Converse Properties: Now we examine the converse of each of the properties we proved. Begin with the property, and prove that the quadrilateral is in fact a parallelogram.

Example 4.
If both pairs of opposite angles of a quadrilateral are equal, then the quadrilateral is a parallelogram. Draw an appropriate diagram, and provide the relevant Given and Prove for this case.
Given: ________
Answer:
Quadrilateral ABCD with m∠A=m∠C, m∠B=m∠D

Prove: _________
Answer:
Quadrilateral ABCD is a parallelogram.

Construction: Label the quadrilateral ABCD. Mark opposite angles as congruent. Draw diagonal \(\overline{B D}\). Label the measures of ∠A and ∠C as x°. Label the measures of the four angles created by \(\overline{B D}\) as r°, s°, t°, and u°.

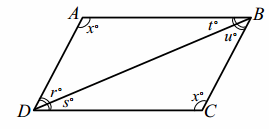
PROOF:
Quadrilateral ABCD with m∠A=m∠C, m∠B=m∠D Given
m∠D=r+s, m∠B=t+u Angle addition
r+s=t+u Substitution
x+r+t=180, x+s+u=180 Angles in a triangle add up to 180°.
r+t=s+u Subtraction property of equality, substitution
r+t-(r+s)=s+u-(t+u) Subtraction property of equality
t-s=s-t Additive inverse property
t-s+(s-t)=s-t+(s-t) Addition property of equality
0=2(s-t) Addition and subtraction properties of equality
0=s-t Division property of equality
s=t Addition property of equality
s=t⇒r=u Substitution and subtraction properties of equality
\(\overline{A B}\) || \(\overline{C D}\), \(\overline{A D}\) || \(\overline{B C}\) If two lines are cut by a transversal such that a pair of alternate interior angles are equal in measure, then the lines are parallel.
Quadrilateral ABCD is a parallelogram. Definition of a parallelogram

Example 5.
If the opposite sides of a quadrilateral are equal, then the quadrilateral is a parallelogram. Draw an appropriate
diagram, and provide the relevant Given and Prove for this case.

Given: ____
Answer:
Quadrilateral ABCD with AB=CD, AD=BC
Prove: ____
Answer:
Quadrilateral ABCD is a parallelogram.

Construction: Label the quadrilateral ABCD, and mark opposite sides as equal. Draw diagonal \(\overline{B D}\).

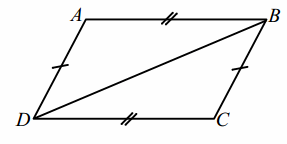
PROOF:
Quadrilateral ABCD with AB=CD, AD=CB Given
BD=DB Reflexive property
△ABD≅ △CDB SSS
∠ABD≅∠CDB,∠ADB≅∠CBD Corresponding angles of congruent triangles are congruent.
\(\overline{A B}\) || \(\overline{C D}\), \(\overline{A D}\) || \(\overline{C B}\) If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
Quadrilateral ABCD is a parallelogram. Definition of a parallelogram

Example 6.
If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. Draw an appropriate diagram, and provide the relevant Given and Prove for this case. Use triangle congruence criteria to demonstrate why the quadrilateral is a parallelogram.

Given: ______
Answer:
Quadrilateral ABCD, diagonals \(\overline{A C}\) and( BD) ̅ bisect each other.
Prove: ____
Answer:
Quadrilateral ABCD is a parallelogram.

Construction: Label the quadrilateral ABCD, and mark opposite sides as equal. Draw diagonals \(\overline{A C}\) and \(\overline{B D}\).

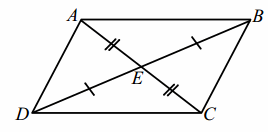
PROOF:
Quadrilateral ABCD, diagonals \(\overline{A C}\) and \(\overline{B D}\) bisect each other. Given
AE=CE, DE=BE Definition of a segment bisector
m∠DEC=m∠BEA, m∠AED=m∠CEB Vertical angles are equal in measure.
△DEC≅ △BEA, △AED≅ △CEB SAS
∠ABD≅∠CDB, ∠ADB≅∠CBD Corresponding angles of congruent triangles are congruent.
\(\overline{A B}\) || \(\overline{C D}\), \(\overline{A D}\) || \(\overline{C B}\) If two lines are cut by a transversal such that a pair of alternate interior angles are congruent, then the lines are parallel.
Quadrilateral ABCD is a parallelogram. Definition of a parallelogram

Example 7.
If the diagonals of a parallelogram are equal in length, then the parallelogram is a rectangle. Complete the diagram, and develop an appropriate Given and Prove for this case.

Given: _____
Answer:
Parallelogram GHIJ with diagonals of equal length, GI=HJ
Prove: ______
Answer:
GHIJ is a rectangle.
Construction: Label the quadrilateral GHIJ. Draw diagonals \(\overline{G I}\) and \(\overline{H J}\).

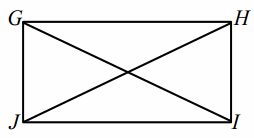
PROOF:
Parallelogram GHIJ with diagonals of equal length, GI=HJ Given
GJ=JG, HI=IH Reflexive property
GH=IJ Opposite sides of a parallelogram are congruent.
△HJG≅ △IGJ, △GHI≅ △JIH SSS
m∠G=m∠J, m∠H=m∠I Corresponding angles of congruent triangles are equal in measure.
m∠G+m∠J=180°, m∠H+m∠I=180° If parallel lines are cut by a transversal, then interior angles on the same side are supplementary.
2(m∠G)=180°, 2(m∠H)=180° Substitution property of equality
m∠G=90°, m∠H=90° Division property of equality
m∠G=m∠J=m∠H=m∠I=90° Substitution property of equality
GHIJ is a rectangle. Definition of a rectangle

Eureka Math Geometry Module 1 Lesson 28 Exercise Answer Key

Opening Exercise

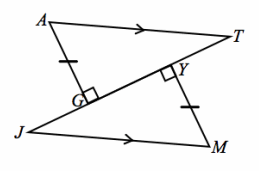
a. If the triangles are congruent, state the congruence.
Answer:
△AGT≅ △MYJ

b. Which triangle congruence criterion guarantees part 1?
Answer:
AAS

c. \(\overline{T G}\) corresponds with
Answer:
\(\overline{J Y}\)

Discussion
How can we use our knowledge of triangle congruence criteria to establish other geometry facts? For instance, what can we now prove about the properties of parallelograms?
To date, we have defined a parallelogram to be a quadrilateral in which both pairs of opposite sides are parallel. However, we have assumed other details about parallelograms to be true, too. We assume that:
→ Opposite sides are congruent.
→ Opposite angles are congruent.
→ Diagonals bisect each other.
Let us examine why each of these properties is true.

Eureka Math Geometry Module 1 Lesson 28 Problem Set Answer Key

Use the facts you have established to complete exercises involving different types of parallelograms.

Question 1.
Given: \(\overline{A B}\) || \(\overline{C D}\), AD=AB, CD=CB
Prove: ABCD is a rhombus.

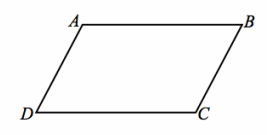
Answer:
Construction: Draw diagonal \(\overline{A C}\).
AD=AB, CD=CB Given
AC=CA Reflexive property
△ADC≅ △CBA SSS
AD=CB, AB=CD Corresponding sides of congruent triangles are equal in length.
AB=BC=CD=AD Transitive property
ABCD is a rhombus. Definition of a rhombus

Question 2.
Given: Rectangle RSTU, M is the midpoint of \(\overline{R S}\) .
Prove: △UMT is isosceles.

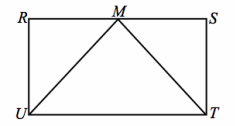
Answer:
Rectangle RSTU Given
RU=ST Opposite sides of a rectangle are congruent.
∠R, ∠S are right angles. Definition of a rectangle
M is the midpoint of \(\overline{R S}\) . Given
RM=SM Definition of a midpoint
△RMU≅ △SMT SAS
\(\overline{U M}\) ≅ \(\overline{T M}\) Corresponding sides of congruent triangles are congruent.
△UMT is isosceles. Definition of an isosceles triangle

Question 3.
Given: ABCD is a parallelogram, \(\overline{R D}\) bisects ∠ADC, \(\overline{S B}\) bisects ∠CBA.
Prove: DRBS is a parallelogram.

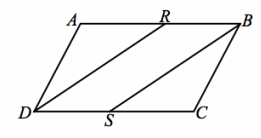
Answer:
ABCD is a parallelogram; Given
\(\overline{R D}\) bisects ∠ADC, \(\overline{S B}\) bisects ∠CBA.
AD=CB Opposite sides of a parallelogram are congruent.
∠A≅∠C, ∠B≅∠D Opposite angles of a parallelogram are congruent.
∠RDA≅∠RDS, ∠SBC≅∠SBR Definition of angle bisector
m∠RDA+m∠RDS=m∠D,m∠SBC+m∠SBR=m∠B Angle addition
m∠RDA+m∠RDA=m∠D,m∠SBC+m∠SBC=m∠B Substitution
2(m∠RDA)=m∠D, 2(m∠SBC)=m∠B Addition
m∠RDA=\(\frac{1}{2}\)m∠D, m∠SBC=\(\frac{1}{2}\)m∠B Division
∠RDA≅∠SBC Substitution
△DAR≅ △BCS ASA
∠DRA≅∠BSC Corresponding angles of congruent triangles are congruent.
∠DRB≅∠BSD Supplements of congruent angles are congruent.
DRBS is a parallelogram. Opposite angles of quadrilateral DRBS are congruent.

Question 4.
Given: DEFG is a rectangle, WE=YG, WX=YZ
Prove: WXYZ is a parallelogram.

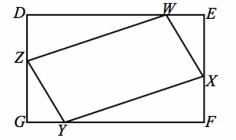
Answer:
DE=FG, DG=FE Opposite sides of a rectangle are congruent.
DEFG is a rectangle; Given
WE=YG, WX=YZ
DE=DW+WE, FG=YG+FY Segment addition
DW+WE=YG+FY Substitution
DW+YG=YG+FY Substitution
DW=FY Subtraction
m∠D=m∠E=m∠F=m∠G=90° Definition of a rectangle
△ZGY, △XEW are right triangles. Definition of right triangle
△ZGY≅ △XEW HL
ZG=XE Corresponding sides of congruent triangles are congruent.
DG=ZG+DZ; FE=XE+FX Partition property or segment addition
DZ=FX Subtraction property of equality
△DZW≅ △FXY SAS
ZW=XY Corresponding sides of congruent triangles are congruent.
WXYZ is a parallelogram. Both pairs of opposite sides of a parallelogram are congruent.

Question 5.
Given: Parallelogram ABFE, CR=DS, \(\overline{A B C}\) and \(\overline{D E F}\) are segments.
Prove: BR=SE

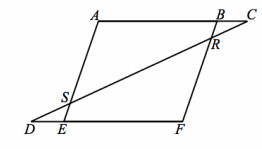
Answer:
\(\overline{A B}\) || \(\overline{F E}\) Opposite sides of a parallelogram are parallel.
m∠BCR=m∠EDS If parallel lines are cut by a transversal, then alternate interior angles are equal in measure.
∠ABF≅∠FEA Opposite angles of a parallelogram are congruent.
∠CBR≅∠DES Supplements of congruent angles are congruent.
CR=DS Given
△CBR≅ △DES AAS
BR=SE Corresponding sides of congruent triangles are equal in length.

Eureka Math Geometry Module 1 Lesson 28 Exit Ticket Answer Key

Given: Equilateral parallelogram ABCD (i.e., a rhombus) with diagonals \(\overline{A C}\) and \(\overline{B D}\)
Prove: Diagonals intersect perpendicularly.

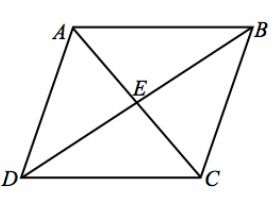
Answer:
Rhombus ABCD Given
AE=CE, DE=BE Diagonals of a parallelogram bisect each other.
AB=BC=CD=DA Definition of equilateral parallelogram
△AED≅ △AEB≅ △CEB≅ △CED SSS
m∠AED=m∠AEB=m∠BEC=m∠CED Corr. angles of congruent triangles are equal in measure.
m∠AED=m∠AEB=m∠BEC=m∠CED=90° Angles at a point sum to 360°. Since all four angles are congruent, each angle measures 90°.