Engage NY Eureka Math Algebra 2 Module 4 Lesson 7 Answer Key
Eureka Math Algebra 2 Module 4 Lesson 7 Example Answer Key
Exercise 1:
When a car is brought to a repair shop for a service, the probability that it will need the transmission fluid replaced is 0.38, the probability that it will need the brake pads replaced is 0.28, and the probability that it will need both the transmission fluid and the brake pads replaced is 0.16. Let the event that a car needs the transmission fluid replaced be T and the event that a car needs the brake pads replaced be B.
a. What are the values of the following probabilities?
i. P(T)
Answer:
0.38
ii. P(B)
Answer:
0.28
iii. P(T and B)
Answer:
0.16
b. Use the addition rule to find the probability that a randomly selected car needs the transmission fluid or the brake pads replaced.
Answer:
P(T or B) = P(T) + P(B) – P(T and B) = 0.38 + 0.28 – 0. 16 = 0.5
Exercise 2:
Josie will soon be taking exams in math and Spanish. She estimates that the probability she passes the math exam is 0.9, and the probability that she passes the Spanish exam is 0.8. She is also willing to assume that the results of the two exams are independent of each other.
a. Using Josie’s assumption of independence, calculate the probability that she passes both exams.
Answer:
P(passes both) = (0. 9)(0. 8) = 0.72
b. Find the probability that Josie passes at least one of the exams. (Hint: Passing at least one of the exams is passing math or passing Spanish.)
Answer:
P(passes math or Spanish) = P(passes math) + P(passes Spanish) – P(passes both)
= 0.9 + 0.8 – 0.72 = 0.98
Example 1: Use of the Addition Rule for Disjoint Events
A set of 40 cards consists of the following:
→ 10 black cards showing squares
→ 10 black cards showing circles
→ 10 red cards showing X’s
→ 10 red cards showing diamonds
A card will be selected at random from the set. Find the probability that the card is black or shows a diamond.
Answer:
The events “is black” and “shows a diamond” are disjoint since there are no black cards that show diamonds. So,
P(black or diamond) = P(biack) + P(diamond)
= \(\frac{20}{40}\) + \(\frac{10}{40}\)
= \(\frac{30}{40}\)
= \(\frac{3}{4}\)
Example 2: Combining Use of the Multiplication and Addition Rules
A red cube has faces labeled 1 through 6, and a blue cube has faces labeled in the same way. The two cubes are rolled. Find the probability of each event.
a. Both cubes show 6’s.
Answer:
P(red shows 6 and blue shows 6) = P(red shows 6) P(blue shows 6) = \(\frac{1}{6}\) \(\frac{1}{6}\) = \(\frac{1}{36}\)
b. The total score is at least 11.
Answer:
P(total is at least 11) = P(red shows 6 and blue shows 5) + P(red shows 5 and blue shows 6) + P(red shows 6 and blue shows 6)
P(total is at least 11) = \(\frac{1}{6}\) . \(\frac{1}{6}\) + \(\frac{1}{6}\) .\(\frac{1}{6}\) + \(\frac{1}{6}\) . \(\frac{1}{6}\)
= \(\frac{1}{36}\) + \(\frac{1}{36}\) + \(\frac{1}{36}\) = \(\frac{1}{12}\)
Exercise 3:
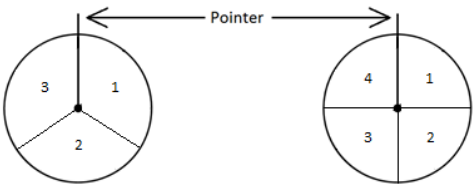
The diagram above shows two spinners. For the first spinner, the scores 1, 2, and 3 are equally likely, and for the second spinner, the scores 1, 2, 3, and 4 are equally likely. Both pointers will be spun. Writing your answers as fractions in lowest terms, find the probability of each event.
a. The total of the scores on the two spinners is 2.
Answer:
P(total = 2) = P(1, 1) = \(\frac{1}{3}\) . \(\frac{1}{4}\) = \(\frac{1}{12}\)
b. The total of the scores on the two spinners is 3.
Answer:
P(total =3) = P(1, 2) + P(2, 1) = \(\frac{1}{3}\) . \(\frac{1}{4}\) + \(\frac{1}{3}\) . \(\frac{1}{4}\) = \(\frac{1}{12}\) + \(\frac{1}{12}\) = \(\frac{2}{12}\) = \(\frac{1}{6}\)
c. The total of the scores on the two spinners is 5.
Answer:
P(total = 5) = P(1, 4) + P(2, 3) + P(3, 2)
= \(\frac{1}{3}\) . \(\frac{1}{4}\) + \(\frac{1}{3}\) . \(\frac{1}{4}\) + \(\frac{1}{3}\) . \(\frac{1}{4}\)
= \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\)
= \(\frac{3}{12}\)
= \(\frac{1}{4}\)
d. The total of the scores on the two spinners is not 5.
Answer:
P(total is not 5) = 1 – P(total is 5) = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
Eureka Math Algebra 2 Module 4 Lesson 7 Problem Set Answer Key
Question 1.
Of the works of art at a large gallery, 59% are paintings, and 83% are for sale. When a work of art is selected at random, let the event that it is a painting be A and the event that it is for sale be B.
a. What are the values of P(A) and P(B)?
Answer:
P(A)= 0.59
P(B) = 0.83
b. Suppose you are told that P(A and B) = 0.51. Find P(A or B).
Answer:
P(A or B) = P(A) + P(B) – P(A and B) = 0.59 + 0.83 – 0.51 = 0.91
c. Suppose now that you are not given the information in part (b), but you are told that the events A and B are independent. Find P(A or B).
Answer:
P(A and B) = P(A)P(B) = (0. 59)(0. 83) = 0.4897
So, P(A or B) = P(A) + P(B) – P(A and B) = 0.59 + 0.83 – 0.4897 = 0.9303.
Question 2.
A traveler estimates that, for an upcoming trip, the probability of catching malaria is 0.18, the probability of catching typhoid is 0.13, and the probability of catching neither of the two diseases is 0.75.
a. Draw a Venn diagram to represent this information.
Answer:
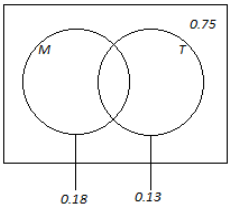
b. Calculate the probability of catching both of the diseases.
Answer:
P(M or T) = 1 – 0.75 = 0.25
By the addition rule:
P(M or T) = P(M) + P(T) – P(M and T)
0,25 = 0. 18 + 0. 13 – P(M and T)
0.25 = 0.31 – P(M and T)
P(M and T) = 0.06
c. Are the events “catches malaria” and “catches typhoid” independent? Explain your answer.
Answer:
P(M and T) = 0.06
P(M)P(T) = (0. 18)(0. 13) = 0.0234
Since these quantities are different, the two events are not independent.
Question 3.
A deck of 40 cards consists of the following:
→ 10 black cards showing squares, numbered 1 – 10
→ 10 black cards showing circles, numbered 1 – 10
→ 10 red cards showing X’s, numbered 1 – 10
→ 10 red cards showing diamonds, numbered 1 – 10
A card will be selected at random from the deck.
a. i. Are the events “the card shows a square” and “the card Is red” disjoint? Explain.
Answer:
Yes. There is no red card that shows a square.
ii. Calculate the probability that the card will show a square or will be red.
Answer:
P(square or red) = P(square) + P(red)
= \(\frac{10}{40}\) + \(\frac{20}{40}\)
= \(\frac{30}{40}\) = \(\frac{3}{4}\)
b. i. Are the events “the card shows a 5” and “the card is red” disjoint? Explain.
Answer:
No. There are red fives in the deck.
ii. Calculate the probability that the card will show a 5 or will be red.
Answer:
P(5 or red) = P(5) + P(red) – P(5 and red)
= \(\frac{4}{40}\) + \(\frac{20}{40}\) – \(\frac{2}{40}\)
= \(\frac{22}{40}\)
= \(\frac{11}{20}\)
Question 4.
The diagram below shows a spinner. When the pointer is spun, it is equally likely to stop on 1, 2, or 3. The pointer will be spun three times. Expressing your answers as fractions in lowest terms, find the probability, and explain how the answer was determined that the total of the values from all three spins is
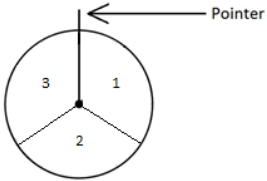
a. 9.
Answer:
The only way to get a total of 9 is to spin a 3, 3 times. Since the probability of spinning a 3 is \(\frac{1}{3^{\prime}}\),
P(total is 9) = P(3, 3, 3) = \(\frac{1}{3}\) . \(\frac{1}{3}\) . \(\frac{1}{3}\)
= \(\frac{1}{27}\)
b. 8.
Answer:
There are 3 ways to get a total of 8. Since the probability of spinning a 1, 2, and 3 are all equally likely (\(\frac{1}{3}\)):
P(total is 8) = P(3, 3, 2) + P(3, 2, 3) + P(2, 3, 3)
= \(\frac{1}{3}\) . \(\frac{1}{3}\) . \(\frac{1}{3}\) + \(\frac{1}{3}\) . \(\frac{1}{3}\) . \(\frac{1}{3}\) + \(\frac{1}{3}\) . \(\frac{1}{3}\) . \(\frac{1}{3}\)
= \(\frac{1}{27}\) + \(\frac{1}{27}\) + \(\frac{1}{27}\)
= \(\frac{3}{27}\) = \(\frac{1}{9}\)
c. 7.
Answer:
There are 6 ways to get a total of 7. Since the probability of spinning a 1, 2, and 3 are all equally likely (\(\frac{1}{3}\)):
P(total is 7) = P(3, 3, 1) + P(3, 1, 3) + P(1, 3, 3) + P(3, 2, 2) + P(2, 3, 2) + P(2, 2, 3)
= 6(\(\frac{1}{3}\) . \(\frac{1}{3}\) . \(\frac{1}{3}\))
= 6(\(\frac{1}{27}\))
= \(\frac{2}{9}\)
Question 5.
A number cube has faces numbered 1 through 6, and a coin has two sides—heads and tails. The number cube will be rolled once, and the coin will be flipped once. Find the probabilities of the following events. (Express your answers as fractions in lowest terms.)
a. The number cube shows a 6.
Answer:
\(\frac{1}{6}\)
b. The coin shows heads.
Answer:
\(\frac{1}{2}\)
c. The number cube shows a 6, and the coin shows heads.
Answer:
\(\frac{1}{6}\) . \(\frac{1}{2}\) = \(\frac{1}{12}\)
d. The number cube shows a 6, or the coin shows heads.
Answer:
P(6 or heads) = P(6) + P(heads) – P(6 and heads)
= \(\frac{1}{6}\) + \(\frac{1}{2}\) – \(\frac{1}{12}\)
= \(\frac{2}{12}\) + \(\frac{6}{12}\) – \(\frac{1}{12}\)
= \(\frac{7}{12}\)
Question 6.
Kevin will soon be taking exams in math, physics, and French. He estimates the probabilities of his passing these exams to be as follows:
→ Math: 0.9
→ Physics: 0.8
→ French: 0.7
Kevin is willing to assume that the results of the three exams are independent of each other. Find the probability of each event.
a. Kevin will pass all three exams.
Answer:
(0.9) (0.8) (0.7) = 0.504
b. Kevin will pass math but fail the other two exams.
Answer:
(0.9) (0.2) (0.3) = 0.054
c. Kevin will pass exactly one of the three exams.
Answer:
P(passes exactly one) = P(passes math, falls physics, fails French) + P(fails math, passes physics. falls French) + P(fails math, fails physics. passes French)
= (0. 9) (0. 2) (0. 3) + (0. 1) (0. 8) (0. 3) + (0. 1) (0. 2) (0. 7)
= 0.092
Eureka Math Algebra 2 Module 4 Lesson 7 Exit Ticket Answer Key
Question 1.
When a call is received at an airline’s call center, the probability that it comes from abroad is 0.32, and the probability that it is to make a change to an existing reservation is 0.38.
a. Suppose that you are told that the probability that a call is both from abroad and is to make a change to an existing reservation is 0. 15. Calculate the probability that a randomly selected call is either from abroad or is to make a change to an existing reservation.
Answer:
P(abroad or change) = P(abroad) + P(change) – P(abroad and change)
= 0.32 + 0.38 – 0. 15
= 0.55
b. Suppose now that you are not given the information in part (a), but you are told that the events “the call is from abroad” and “the call is to make a change to an existing reservation” are independent. What is the probability that a randomly selected call Is either from abroad or is to make a change to an existing reservation?
Answer:
P(abroad and change) = P(abroad) P(change)
= (0. 32) (0. 38)
= 0.1216
So,
P(abroad or change) = P(abroad) + P(change) – P(abroad and change)
= 0.32 + 0.38 – 0. 1216
= 0. 5784.
Question 2.
A golfer will play two holes of a course. Suppose that on each hole the player will score 3, 4, 5, 6, or 7, with these five scores being equally likely. Find the probability, and explain how the answer was determined that the player’s total score for the two holes will be
a. 14.
Answer:
The only way to have o total score of 14 Is if the player scores 7 on each hole, which is P(7) . P(7). Each of the scores is equally likely, so P(7) = \(\frac{1}{5}\) = 0.2.
P(total = 14) = P(7) . P(7) = (0.2) (0.2) = 0.04
b. 12.
Answer:
There are three ways to hove a total score of 12. The player could score 7 on the first hole and 5 on the second. The player could score 6 on the first hole and 6 on the second. Finally, the player could score 5 on the first hole and7on the second. Again, all of the scores are equally likely, so P(5) = P(6) = P(7) = 0.2.
P(total = 12) = P(7, 5) + P(6, 6) + P(5, 7)
= (0.2)(0.2) + (0.2)(0.2) + (0.2)(0.2)
= 0. 04 + 0. 04 + 0. 04
= 0.12