Engage NY Eureka Math Algebra 2 Module 3 Lesson 21 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 21 Exploratory Challenge Answer Key
Exploratory Challenge:
Your task is to compare graphs of base b logarithm functions to the graph of the common logarithm function f(x) = log(x) and summarize your results with your group. Recall that the base of the common logarithm function is 10. A graph of f is provided below.
a. Select at least one base value from this list: \(\frac{1}{10}\), \(\frac{1}{2}\), 2, 5, 20, 100. Write a function in the form g(x) = log(x) for your selected base value, b.
Answer:
Students should use one of the numbers from the list to write their function. The sample solutions will use g(x) = log\(\frac{1}{2}\)(x).
b. Graph the functions f and g in the same viewing window using a graphing calculator or other graphing application, and then add a sketch of the graph of g to the graph off shown below.
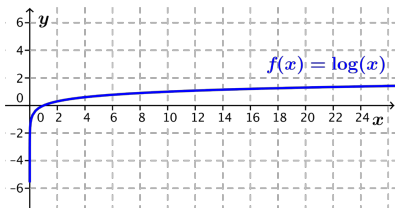
Answer:
The graph of f(x) = log(x) is shown in blue, and the graph of g(x) = log\(\frac{1}{2}\)(x) is shown in green.
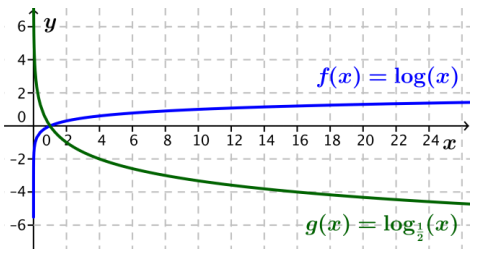
c. Describe how the graph of g for the base you selected compares to the graph of f(x) = log(x).
Answer:
Answers will vary depending on the base selected. For example, when the base is 20, the graph of g appears to be a vertical scaling of the common logarithm function by a factor less than 1.
d. Share your results with your group and record observations on the graphic organizer below. Prepare a group presentation that summarizes the group’s findings.

Answer:

Eureka Math Algebra 2 Module 3 Lesson 21 Exercise Answer Key
Exercise 1:
Use the change of base property to rewrite each logarithmic function in terms of the common logarithm function.

Answer:

Eureka Math Algebra 2 Module 3 Lesson 21 Example Answer Key
Example 1: The Graph of the Natural Logarithm Function f(x) = ln(x)
Graph the natural logarithm function below to demonstrate where it sits in relation to the graphs of the base-2 and base-10 logarithm functions.
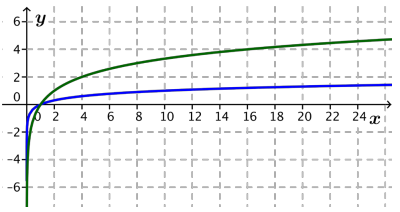
Answer:
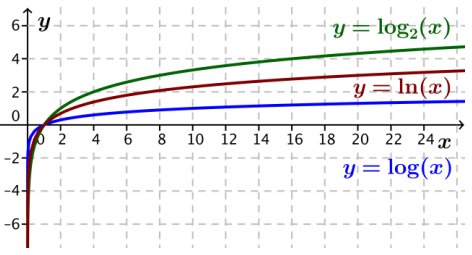
Example 2:
Graph each function by applying transformations of the graphs of the natural logarithm function.
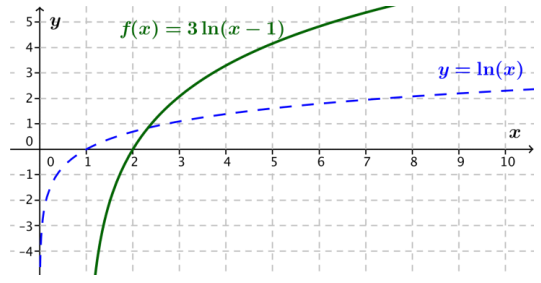
a. f(x) = 3 ln (x – 1)
Answer:
The graph of f is the graph of y = ln(x) shifted horizontally 1 unit to the right, stretched vertically by a factor of 3.
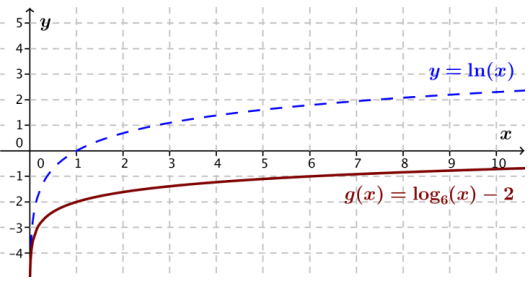
b. g(x) = log6(x) – 2
Answer:
First, write g as a natural logarithm function.
g(x) = \(\frac{\ln (x)}{\ln (6)}\) – 2
Since \(\frac{1}{\ln (6)}\) ≈ 0.558, the graph of g will be the graph of y = ln(x) scaled vertically by a factor of approximately 0.56 and translated down 2 units.
Eureka Math Algebra 2 Module 3 Lesson 21 Problem Set Answer Key
Question 1.
Rewrite each logarithmic function as a natural logarithm function.
a. f(x) = log5(x)
Answer:
f(x) = \(\frac{\ln (x)}{\ln (5)}\)
b. f(x) = log2(x – 3)
Answer:
f(x) = \(\frac{\ln (x-3)}{\ln (2)}\)
c. f(x) = log2(\(\frac{x}{3}\))
Answer:
f(x) = \(\frac{\ln (x)}{\ln (2)}\) – \(\frac{\ln (3)}{\ln (2)}\)
d. f(x) = 3 – log(x)
Answer:
f(x) = 3 – \(\frac{\ln (x)}{\ln (10)}\)
e. f(x) = 2log(x + 3)
Answer:
f(x) = \(\frac{2}{\ln (10)}\)ln(x + 3)
f. f(x) = log5(25x)
Answer:
f(x) = 2 + \(\frac{\ln (x)}{\ln (5)}\)
Question 2.
Describe each function as a transformation of the natural logarithm function f(x) = ln(x).
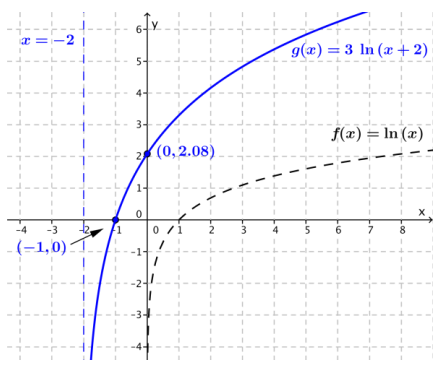
a. g(x) = 3ln(x + 2)
Answer:
The graph of g is the graph of f translated 2 units to the left and scaled vertically by a factor of 3.
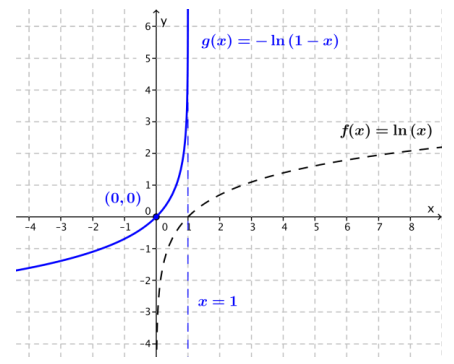
b. g(x) = -ln(1 – x)
Answer:
The graph of g is the graph of f translated 1 unit to the right, reflected about x = 1, and then reflected about the horizontal axis.
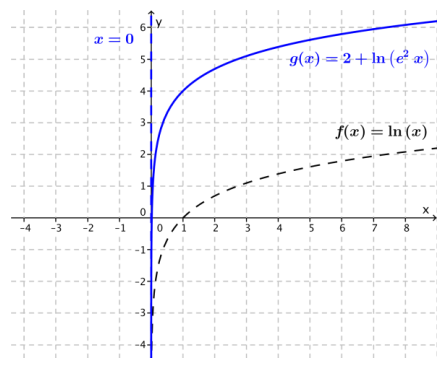
c. g(x) = 2 + ln(e2x)
Answer:
The graph of g is the graph off translated up 4 units.
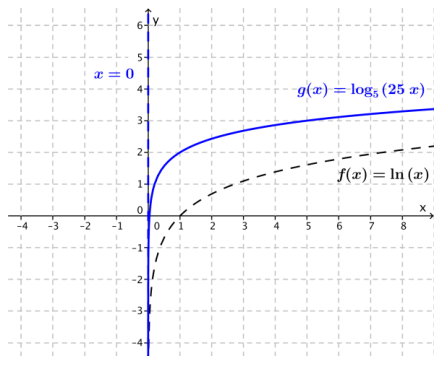
d. g(x) = log5(25x)
Answer:
The graph of g is the graph off translated up 2 units and scaled vertically by a factor of \(\frac{1}{\ln (5)}\)
Question 3.
Sketch the graphs of each function In Problem 2, and identify the key features including intercepts, intervals where the function is increasing or decreasing, and the vertical asymptote.
Answer:
a. The equation of the vertical asymptote is x = -2. The x-intercept is -1. The function is increasing for all x > -2. The y-intercept is approximately 2.079.
b. The equation of the vertical asymptote is x = 1. The x-intercept is 0. The function is increasing for all x < 1. The y-intercept is 0.
c. The equation of the vertical asymptote is x = 0. The x-intercept is approximately 0.018. The function is increasing for all x > 0.
d. The equation of the vertical asymptote is x = 0. The x-intercept is 0.04. The function is increasing for all x > 0.
Question 4.
Solve the equation 1 – ex – 1 = ln(x) graphically, without using a calculator.
Answer:
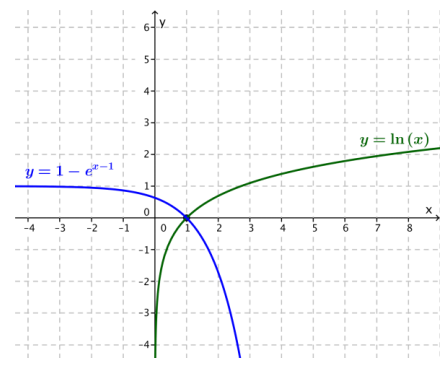
It appears that the two graphs intersect at the point (1, 0). Checking, we see that 1 – e1 – 1 = 1 – 1 = 0, and we know that ln(1) = 0, so when x = 0, we have 1 – ex – 1 = ln(x). Thus 0 is a solution to this equation. From the graph, it is the only solution.
Question 5.
Use a graphical approach to explain why the equation log(x) = ln(x) has only one solution.
Answer:
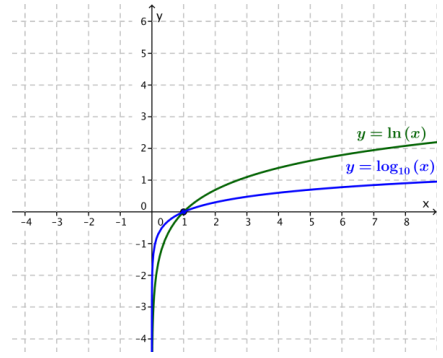
The graphs intersect in only one point(1, 0), so the equation has only one solution.
Question 6.
Juliet tried to solve this equation as shown below using the change of base property and concluded there is no solution because ln(10) ≠ 1. Construct an argument to support or refute her reasoning.
log(x) = ln(x)
\(\frac{\ln (x)}{\ln (10)}\) = ln(x)
(\(\frac{\ln (x)}{\ln (10)}\)) \(\frac{1}{\ln (x)}\) = (ln(x)) \(\frac{1}{\ln (x)}\)
\(\frac{1}{\ln (10)}\) = 1
Answer:
Juliet’s approach works as long as ln(x) ≠ 0, which occurs when x = 1. The solution to this equation is 1. When you divide both sides of an equation by an algebraic expression, you need to Impose restrictions so that you are not dividing by 0. In this case, Juliet divided by ln(x), which is not valid if x = 1. This division caused the equation in the third and final lines of her solution to have no solution; however, the original equation is true when x is 1.
Question 7.
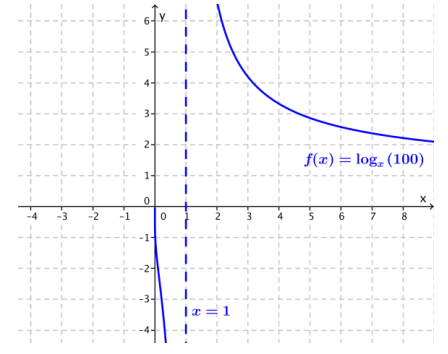
Consider the function f given by f(x) = logx(100) for x > 0 and x ≠ 1.
a. What are the values of f(100), f(10), and f√10)?
Answer:
f(100) = 1, f(10) = 2, f(√10) = 4
b. Why is the value 1 excluded from the domain of this function?
Answer:
The value 1 is excluded from the domain because 1 is not a base of an exponential function since it would produce the graph of a constant function. Since logarithmic functions by definition are related to exponential functions, we cannot have a logarithm with base 1.
c. Find a value x so that f(x) = 0.5.
Answer:
logx(100) = 0.5
x0.5 = 100
x = 10,000
The what of x that satisfies this equation is 10,000.
d. Find a value w so that f(w) = -1.
Answer:
The wise of w that satisfies this equation is \(\frac{1}{100}\).
e. Sketch a graph of y = logx(100) for x > 0 and x ≠ 1.
Answer:
Eureka Math Algebra 2 Module 3 Lesson 21 Exit Ticket Answer Key
Question 1.
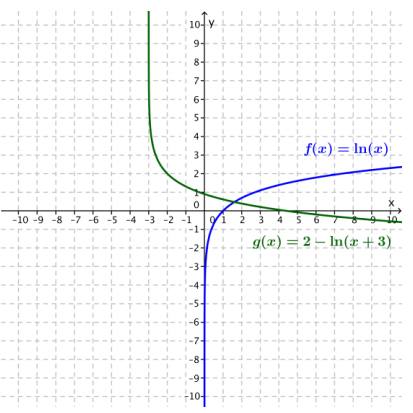
a. Describe the graph of g(x) = 2 – ln(x + 3) as a transformation of the graph of f(x) = ln(x).
Answer:
The graph of g is the graph of f translated 3 units to the left, reflected about the horizontal axis, and translated up 2 units.
b. Sketch the graphs of f and g by hand.
Answer:
Question 2.
Explain where the graph of g(x) = log3(2x) would sit in relation to the graph of f(x) = ln(x). Justify your answer using properties of logarithms and your knowledge of transformations of graph of functions.
Answer:
Since log3(2x) = \(\frac{\ln (2 x)}{\ln (3)}\) = \(\frac{\ln (x)}{\ln (3)}\) + \(\frac{\ln (x)}{\ln (3)}\), the graph of g would be a vertical shift and a vertical scaling by a factor greater than 1 of the graph of f. The graph of g will lie vertically above the graph of f.