Eureka Math Algebra 2 Module 1 Lesson 34 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 34 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 34 Example Answer Key

Example 1.
Derive an Equation for a Parabola Consider a parabola P with distance p > 0 between the focus with coordinates (0, \(\frac{1}{2}\)p), and directrix y = –\(\frac{1}{2}\)p. What is the equation that represents this parabola?

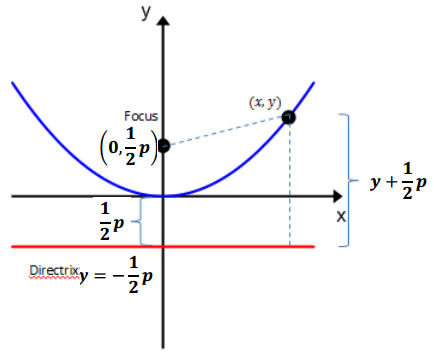
Answer:
→ What are the coordinates of the vertex?
The coordinates of the vertex are (0, 0).

→ Find a formula for the distance between the focus and the point (x, y).
\(\sqrt{(x-0)^{2}+\left(y-\frac{1}{2} p\right)^{2}}\)

→ Find a formula for the distance between (x, y) and the directrix.

→ By the definition of a parabola, these distances are equal. Create an equation.
y + \(\frac{1}{2}\)p = \(\sqrt{(x-0)^{2}+\left(y-\frac{1}{2} p\right)^{2}}\)

→ Solve the equation for y.
Start by squaring both sides. When you expand the squared binomials, the y² and \(\frac{1}{4}\) p² terms drop out of the equation. You may need to provide some additional scaffolding for students who are still not fluent with expanding binomial expressions.

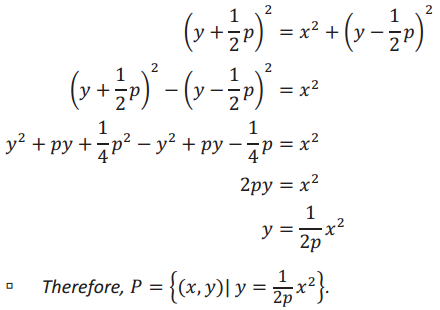
We can confirm the conjecture that the graph of a parabola vertically shrinks as p increases because the expression \(\frac{1}{2 p}\) will get smaller as p gets larger; thus, the parabola appears flatter.

Example 2.
THEOREM: Given a parabola P given by a directrix L and a focus F in the Cartesian plane, then P is congruent to the graph of y = \(\frac{1}{2 p}\)x², where p is the distance from F to L.

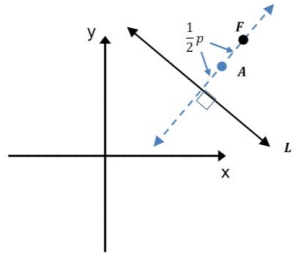
Answer:
PROOF:

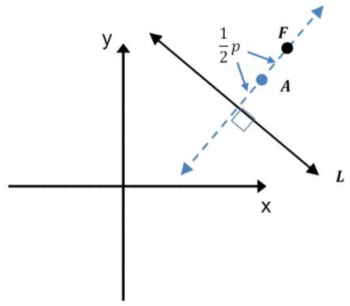
Let A be the point on the perpendicular line to L that passes through F, which is the midpoint of the line segment between F and L.

Translate A to the origin A’ = (0, 0) using a translation. Then, F translates to F’ and L translates to L’.

Next, rotate F’ and L’ about (0, 0) until F” = (o, \(\frac{1}{2}\)p) and L” = {(x, y) | y = –\(\frac{1}{2}\)p}. We are guaranteed we can do this because A’ is on the line perpendicular to L’ that passes through F’.

The translations described above are shown below.

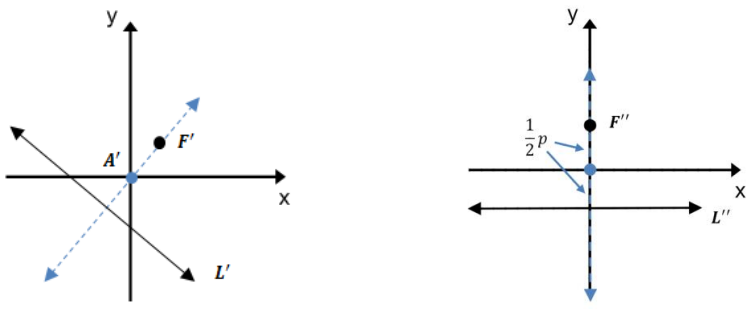
Since P is determined by F and L, the first translation takes P to a parabola P’ such that P ≅ P’. The rotation takes P’ to a parabola P” such that P’ ≅ P”. Therefore, P ≅ P” by transitivity.

Now, by Example 1 above,
P” = {(x, y) | y = \(\frac{1}{2 p}\)x²
that is, P” is the graph of the equation y = \(\frac{1}{2 p}\)x², which is what we wanted to prove.

Eureka Math Algebra 2 Module 1 Lesson 34 Opening Exercise Answer Key

Are all parabolas congruent? Use the following questions to support your answer.

a. Draw the parabola for each focus and directrix given below.

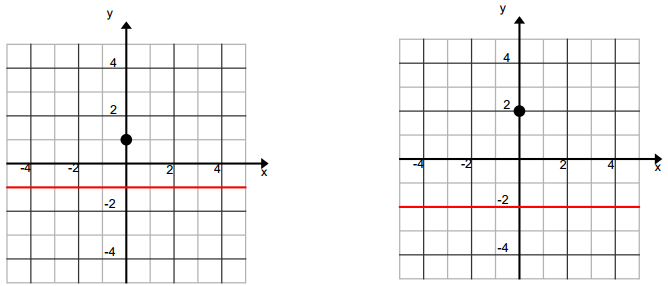
Answer:

b. What do we mean by congruent parabolas?
Answer:
Two parabolas would be congruent if we could find a sequence of rigid motions that takes one parabola onto the other. We could translate the vertex of the first one onto the vertex of the second one, then rotate the image of the first one so that the directrices are parallel and both parabolas open in the same direction. If the transformed first parabola coincides with the original second parabola, then the two original parabolas are congruent.

c. Are the two parabolas from part (a) congruent? Explain how you know.
Answer:
These two parabolas are not congruent. They have the same vertex but different y-values for each x in the domain, except for the point (0, 0). If we translate the first one somewhere else, then the vertices will not align. If we reflect or rotate, then both parabolas will not open upward. There is no rigid transformation or set of transformations that takes the graph of one parabola onto the other.

d. Are all parabolas congruent?
Answer:
No, we just found two that are not congruent.

e. Under what conditions might two parabolas be congruent? Explain your reasoning.
Answer:
Once we align the vertices and get the directrices parallel and parabolas opening in the same direction through rotation or reflection, the parabolas will have the same shape if the focus and directrix are aligned. Thus, two parabolas will be congruent if they have the same distance between the focus and directrix.

Eureka Math Algebra 2 Module 1 Lesson 34 Exercise Answer Key

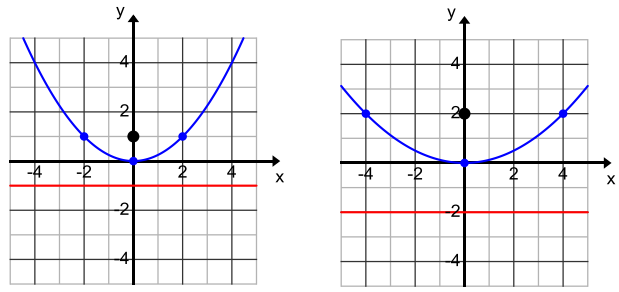
Exercise 1.
Draw the parabola with the given focus and directrix.

Answer:

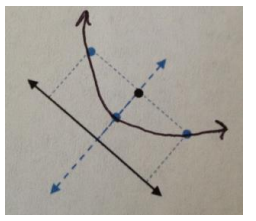
Exercise 2.
Draw the parabola with the given focus and directrix.

Answer:

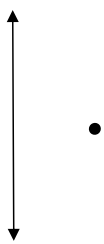
Exercise 3.
Draw the parabola with the given focus and directrix.

Answer:

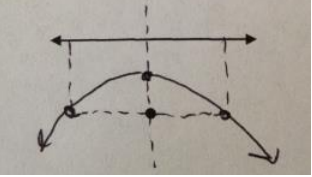
Exercise 4.
What can you conclude about the relationship between the parabolas in Exercises 1 – 3?
Answer:
The parabolas are all the same size and shape because the distance between the focus and the directrix stayed the same. These parabolas should be congruent.

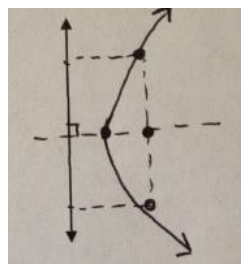
Exercise 5.
Let p be the number of units between the focus and the directrix, as shown. As the value of p increases, what happens to the shape of the resulting parabola?

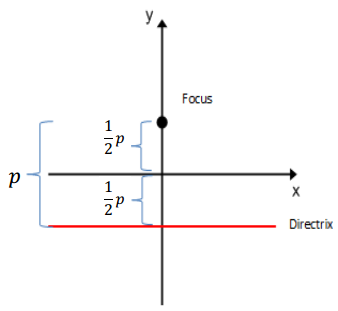
Answer:
As the value of p increases, the graph is dilated and shrinks vertically compared to graphs with a smaller value of p. It appears to get flatter.

Exercise 6.
Restate the results of the theorem from Example 2 in your own words.
Answer:
All parabolas that have the same distance between the focus point and the directrix are congruent

Exercise 7.
Create the equation for a parabola that is congruent to y = 2x². Explain how you determined your answer.
Answer:
y = 2x² + 1. As long as the coefficient of the x² term is the same, the parabolas will be congruent

Exercise 8.
Create an equation for a parabola that IS NOT congruent to y = 2x². Explain how you determined your answer.
Answer:
y = x². As long as the coefficient of the x² term is different the parabolas will not be congruent

Exercise 9.
Write the equation for two different parabolas that are congruent to the parabola with focus point (0, 3) and directrix line y = – 3.
Answer:
The distance between the focus and the directrix Is 6 unIts. Therefore, any parabola with a coefficient of \(\frac{1}{2 p}=\frac{1}{2(6)}=\frac{1}{12}\) will be congruent to this parabola Here are two options: y = \(\frac{1}{12}\)x² + 1 and x = \(\frac{1}{12}\)y².

Eureka Math Algebra 2 Module 1 Lesson 34 Problem Set Answer Key

Question 1.
Show that if the point with coordinates (x, y) Is equidistant from (4, 3), and the line y = 5, then y = – \(\frac{1}{4}\) x²+ 2x.
Answer:
Students might start with the equation \(\sqrt{(x-4)^{2}+(y-3)^{2}}\) = 5 – y and solve for y as follows:
\(\sqrt{(x-4)^{2}+y^{2}-6 y+9}\) = 5 – y
(x – 4)² + y² – 6y + 9 = 25 – 10y + y²
(x – 4)² = – 4y + 16
4y = -(x – 4)² + 16
y = –\(\frac{1}{4}\)(x² – 8x + 16) + 4
y = –\(\frac{1}{4}\)x² + 2x.
Or, they might apply what we have learned about the vertex form of the equation of a parabola. Since the directrix is above the focus, we know the parabola opens downward, so p will be negative. Since the distance from the point (4, 3) to the line y = 5 is 2 units, we know that p = -2. The vertex is halfway between the focus and directrix, so the coordinates of the vertex are (4, 4). Then, the vertex form of the equation that represents the parabola is
y = –\(\frac{1}{4}\) (x – 4)² + 4
y = – \(\frac{1}{4}\) x² + 2x.

Question 2.
Show that if the point with coordinates (x, y) is equidistant from the point (2, 0) and the line y = – 4, then y = \(\frac{1}{8}\)(x – 2)² – 2.
Answer:
Students might start with the equation \(\sqrt{(x-2)^{2}+(y-0)^{2}}\) = y + 4, and then solve it for y, or they might apply the vertex form of the equation of a parabola. Since the vertex is above the directrix, we know that the parabola opens upward, and p > 0. Since the distance from the point (2, 0) to the line y = – 4 is 4 units, we know that p = 4. The vertex is halfway between the focus and directrix, so the vertex is (2, – 2). Thus, the equation that represents the parabola is y = \(\frac{1}{8}\)(x – 2)² – 2.

Question 3.
Find the equation of the set of points which are equidistant from (0,2) and the x-axis. Sketch this set of points
Answer:

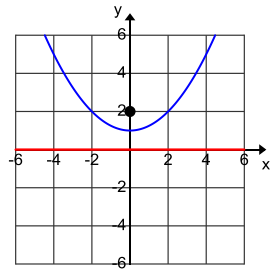
The focus is (0, 2), and the directrix is the x-axis. Thus, the vertex is the y point (0, 1), which is halfway between the vertex and directrix. Since the parabola opens upward, p > 0, so p = 2. Then, the vertex form of the equation of the parabola is y = \(\frac{1}{4}\)x² + 1.

Question 4.
Find the equation of the set of points which are equidistant from the origin and the line y = 6. Sketch this set of points.
Answer:
y = –\(\frac{1}{12}\)x² + 3

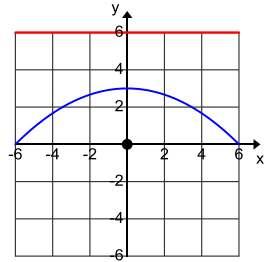
Question 5.
Find the equation of the set of points which are equidistant from (4, – 2) and the line y = 4. Sketch this set of points.
Answer:
y = – \(\frac{1}{12}\)(x – 4)² + 1

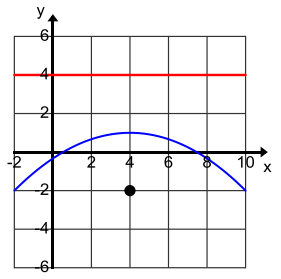
Question 6.
Find the equation of the set of points which are equidistant from (4, 0) and the y-axis. Sketch this set of points.
Answer:
x = \(\frac{1}{8}\)y² + 2

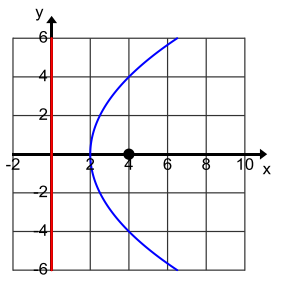
Question 7.
Find the equation of the set of points which are equidistant from the origin and the line x = —2. Sketch this set of points.
Answer:
x = \(\frac{1}{4}\)y² – 1

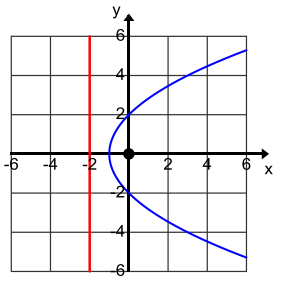
Question 8.
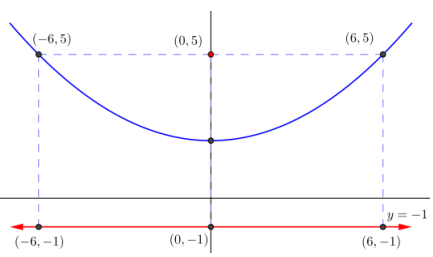
Use the definition of a parabola to sketch the parabola defined by the given focus and directrix.
a. Focus: (0, 5) Directrix: y = – 1
Answer:

b. Focus: (- 2, 0) Directrix: y-axis
Answer:

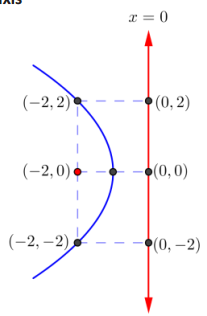
c. Focus: (4, – 4) Directrix: x-axis
Answer:

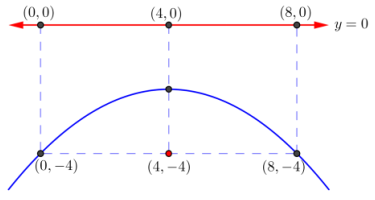
d. Focus: (2, 4) Directrix: y = – 2
Answer:

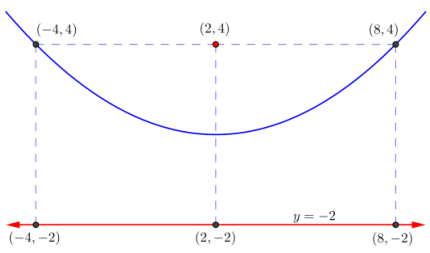
Question 9.
Find an analytic equation for each parabola described In Problem 8.
Answer:
a. p = {(x, y) | y = \(\frac{1}{12}\)x² + 2}; thus, P is the graph of the equation y = \(\frac{1}{12}\) x² + 2.
b. P = {(x,y) |x = – \(\frac{1}{4}\)y² – 1)}; thus, Pis the graph of the equation x = –\(\frac{1}{4}\)y² – 1.
c. p = {(x, y) | y = –\(\frac{1}{8}\)(x – 4)² – 2};thus, P is the graph of the equation y = –\(\frac{1}{8}\)(x – 4)² – 2.
d. P = {(x, y) | y = \(\frac{1}{12}\)(x – 2)² + 1); thus, P is the graph of the equation y = \(\frac{1}{4}\) (x – 2)² + 1.

Question 10.
Are any of the parabolas described in Problem 9 congruent? Explain your reasoning.
Answer:
(a) p = 6, (b) p = 2, (c) p = 4, and (d) p = 6; therefore, the parabolas in parts (a) and (d) are congruent because they have the same distance between the focus and directrix.

Question 11.
Sketch each parabola, labeling its focus and directrix.
Answer:
Each sketch should have the appropriate vertex, focus, and directrix and be fairly accurate. Sketches for parts (a) and (c) are shown.
a. y = \(\frac{1}{2}\)x² + 2
Distance between focus and directrix is 1 unit, vertex (0, 2), focus (0, 2.5), directrix y= 1.5

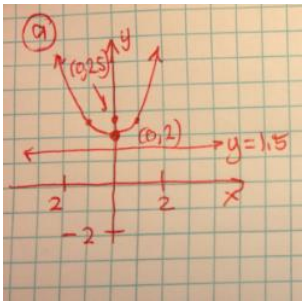
b. y = – \(\frac{1}{4}\)x² + 1
Answer:
Distance between focus and directrix is 2 units, vertex (0, 1), focus (0, 0), directrix y = 2

c. x = \(\frac{1}{8}\)y²
Answer:
Distance between focus and directrix is4 units, vertex (0, 0), focus (2, 0), directrix x = – 2

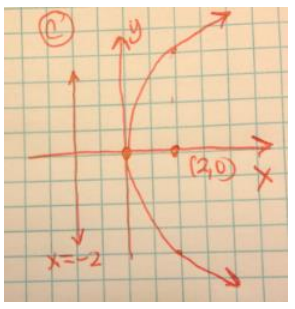
d. x = \(\frac{1}{2}\)y² + 2
Answer:
Distance between focus and directrix is 1 unit, vertex (2, 0), focus (2.5, 0), directrix x = 1.5

e. y = \(\frac{1}{10}\)(x – 1)² – 2
Answer:
Distance between focus and directrix is 5 units, vertex (1, – 2), focus (1, 0.5), directrix y = – 4.5

Question 12.
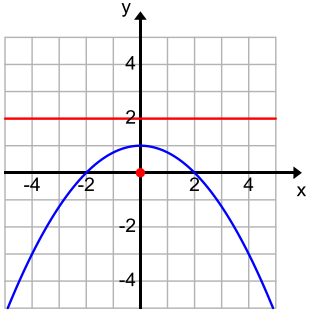
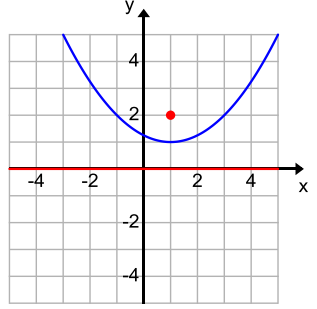
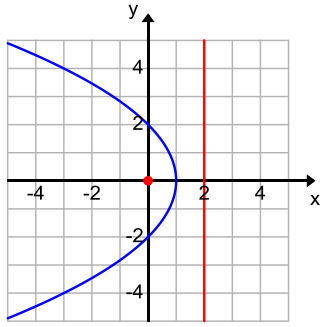
Determine which parabolas are congruent to the parabola with equation y = \(\frac{1}{4}\)x²
a.

b.

c.

d.

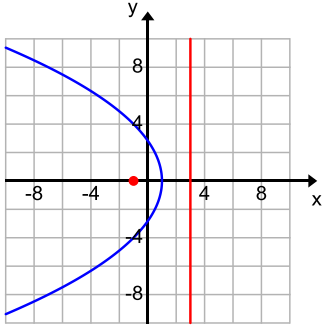
Answer:
Parabolas (a), (b), and (c) are congruent because all have p = 2. Parabola (d) has p = 1, so it is not congruent to the others.

Question 13.
Determine which equations represent the graph of a parabola that is congruent to the parabola shown to the right.
a. y = \(\frac{1}{20}\)x²
b. y = \(\frac{1}{10}\)x² + 3
c. y = –\(\frac{1}{20}\)x² + 8
d. y = \(\frac{1}{5}\)x² + 5
e. x = \(\frac{1}{10}\)y²
f. x = \(\frac{1}{5}\)(y – 3)²
g. x = \(\frac{1}{20}\)y² + 1

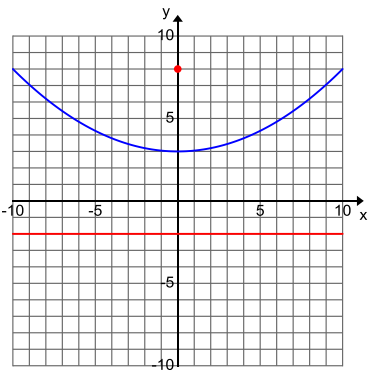
Answer:
The parabolas in parts (a), (c), and (g) are congruent and are congruent to the parabola shown. They all have the same distance of 10 units between the focus and the directrix like the parabola shown.

Question 14.
Jemma thinks that the parabola with equation y = \(\frac{1}{3}\)x² is NOT congruent to the parabola with equation y = –\(\frac{1}{3}\)x² + 1. Do you agree or disagree? Create a convincing argument to support your reasoning.
Answer:
Jemma is wrong. These two parabolas are congruent. If you translate the graph of y = –\(\frac{1}{3}\) x² + 1 down one unit and then reflect the resulting graph about the x-axis, the resulting parabola will have equation y = \(\frac{1}{3}\)x². Alternately, the focus and directrix of each parabola are the same distance apart, 1.5 units.

Question 15.
Let P be the parabola with focus (2, 6) and directrix y = —2.
a. Write an equation whose graph is a parabola congruent to P with focus (0, 4).
Answer:
The equation y = \(\frac{1}{16}\)x² is one option. The directrix for this parabola is y = – 4. Another possible solution would be the parabola with focus (0, 4) and directrix y = 12. The equation would be y = –\(\frac{1}{16}\)x² + 8.

b. Write an equation whose graph is a parabola congruent to P with focus (0, 0).
Answer:
y = \(\frac{1}{16}\)x² – 4

c. Write an equation whose graph is a parabola congruent to P with the same directrix but different focus.
Answer:
The focus would be a reflection of the originalfocus across the directrix, or (2, —10). The equation would be
y = –\(\frac{1}{16}\)(x – 2)² – 6.

d. Write an equation whose graph is a parabola congruent to P with the same focus but with a vertical directrix.
Answer:
x = \(\frac{1}{16}\)(y – 6)² – 2 or x = –\(\frac{1}{16}\)(y – 6)² + 8

Question 16.
Let P be the parabola with focus (0, 4) and directrix y = x.

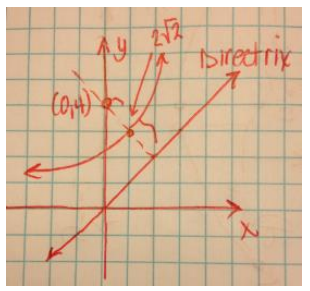
a. Sketch this parabola.
Answer:
The sketch is shown to the right.

b. By how many degrees would you have to rotate P about the focus to make the directrix line horizontal?
Answer:
One possible answer is a clockwise rotation of 45°.

c. Write an equation in the form y = \(\frac{1}{2 a}\)x² whose graph is a parabola that is congruent to P.
Answer:
The distance between the focus and the directrix is 2√2. The equation is y = \(\frac{1}{4 \sqrt{2}}\)x².

d. Write an equation whose graph is a parabola with a vertical directrix that is congruent to P.
Answer:
Since the exact focus and directrix are not specified, there are infinitely many possible parabolas. A vertical directrix does require that the y-term be squared. Thus, x = \(\frac{1}{4 \sqrt{2}}\)y² satisfies the conditions specified in the problem.

e. Write an equation whose graph is P’, the parabola congruent to P that results after P is rotated clockwise 45° about the focus.
Answer:
The directrix will be y = 4 – 2√2. The equation is y = \(\frac{1}{4 \sqrt{2}}\)x² + 4 – √2.

f. Write an equation whose graph is P”, the parabola congruent to P that results after the directrix of P is rotated 45° about the origin.
Answer:
The focus will be (2√2, 2√2), and the directrix will be the x-axis. The equation is y = \(\frac{1}{4 \sqrt{2}}\) (x – 2√2)² + √2.

Extension:

Question 17.
Consider the function f(x) = \(\frac{2 x^{2}-8 x+9}{-x^{2}+4 x-5}\), where x is a real number.
a. Use polynomial division to rewrite f in the form f(x) = q + \(\frac{r}{-x^{2}+4 x-5}\) for some real numbers q and r.
Answer:
Using polynomial division, f(x) = – 2 + \(\frac{-1}{-x^{2}+4 x-5}\)

b. Find the x-value where the maximum occurs for the function f without using graphing technology. Explain how you know.
Answer:
We can rewrite f as f(x) = – 2 + \(\frac{1}{x^{2}-4 x+5}\). Since x² – 4x + 5 = (x – 2)² + 1, the graph of y = x² – 4x + 5 is a parabola with vertex (2, 1) that opens upward. Thus, the lowest point on the graph is (2, 1). The function f will take on its maximum value when \(\frac{1}{x^{2}-4 x+5}\) is maximized; this happens when the value of x² – 4x + 5 is minimized. Since we have already seen that x² – 4x + 5 is minimized at x = 2, the expression \(\frac{1}{x^{2}-4 x+5}\) takes on its maximum value when x = 2, and, thus, the original function f takes on its maximum value when x = 2.

Eureka Math Algebra 2 Module 1 Lesson 34 Exit Ticket Answer Key

Which parabolas shown below are congruent to the parabola that is the graph of the equation y = \(\frac{1}{12}\)x²? Explain how you know.
a.

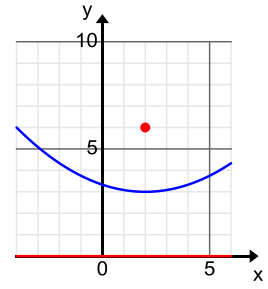
b.

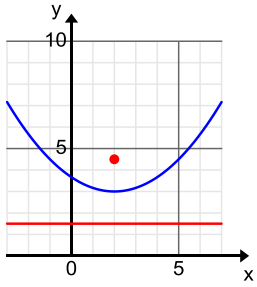
c.

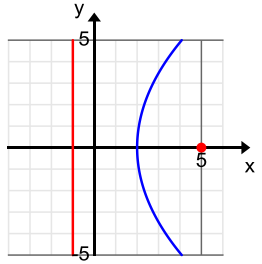
Answer:
The p-value is 6. So, any parabola where the distance between the focus and the directrix is equal to 6 units will be congruent to the parabola that is the graph of the equation y = \(\frac{1}{12}\)x². of the parabolas shown below, (a) and (c) meet this condition, but (b) does not.