Engage NY Eureka Math Algebra 1 Module 1 Lesson 9 Answer Key
Eureka Math Algebra 1 Module 1 Lesson 9 Exercise Answer Key
Exercise 1.
a. Gisella computed 342×23 as follows:
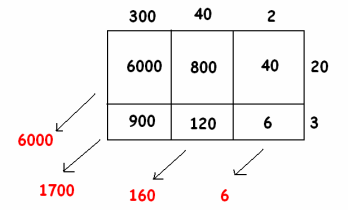
Can you explain what she is doing? What is her final answer?
Answer:
She is using an area model, finding the area of each rectangle and adding them together. Her final answer is 7,866.
Use a geometric diagram to compute the following products:
b. (3x2+4x+2)×(2x+3)
Answer:
6x3+17x2+16x+6
c. (2x2+10x+1)(x2+x+1)
Answer:
2x4 + 12x3+13x2+11x + 1
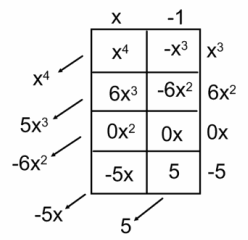
d. (x-1)(x3+6x2-5)
Answer:
x4+5x3-6x2-5x+5
Ask the students:
→ What do you notice about the terms along the diagonals in the rectangles you drew?
Encourage students to recognize that in parts (b) and (c), the terms along the diagonals were all like terms; however, in part (d) one of the factors has no x-term. Allow students to develop a strategy for dealing with this, concluding with the suggestion of inserting the term + 0x, for a model that looks like the following:
Students may naturally ask about the division of polynomials. This topic will be covered in Algebra II, Module 1. The extension challenge at the end of the lesson, however, could be of interest to students inquiring about this.
→ Could we have found this product without the aid of a geometric model? What would that look like?
Go through the exercise applying the distributive property and collecting like terms. As a scaffold, remind students that variables are placeholders for numbers. If x=5, for example, whatever the quantity on the right is (270), you have
5-1 of “that quantity,” or 5 of “that quantity” minus 1 of “that quantity.” Similarly we have x of that quantity, minus 1 of that quantity.
(x-1)(x3+6x2-5)
x(x3+6x2-5)-1(x3+6x2-5)
x4+6x3-5x- x3-6x2+5
x4+5x3-6x2-5x+5
Exercise 2.
Multiply the polynomials using the distributive property: (3x2+x-1)(x4 – 2x + 1).
Answer:
3x2 (x4-2x+1)+x(x4-2x+1)-1(x4-2x+1)
3x6-6x3+3x2+x5-2x2+x-x4+2x-1
3x6+x5-x4-6x3+x2+3x-1
Exercise 3.
The expression 10x2+6x3 is the result of applying the distributive property to the expression 2x2 (5+3x). It is also the result of applying the distributive property to 2(5x2+3x3) or to x(10x+6x2), for example, or even to
1∙(10x2+6x3).
For (a) to (j) below, write an expression such that if you applied the distributive property to your expression, it would give the result presented. Give interesting answers!
a. 6a+14a2
b. 2x4+2x5+2x10
c. 6z2-15z
d. 42w3-14w+77w5
e. z2 (a+b)+z3 (a+b)
f. \(\frac{3}{2}\) s2+ \(\frac{1}{2}\)
g. 15p3 r4-6p2 r5+9p4 r2+3\(\sqrt{2}\) p3 r6
h. 0.4x9-40x8
i. (4x+3)(x2+x3 )-(2x+2)(x2+x3)
j. (2z+5)(z-2)-(13z-26)(z-3)
Answer:
Some possible answers:
a. 2a(3+7a) or 2(3a+7a2) or a(6+14a)
b. 2x4 (1+x+x6) or x(2x3+2x4+2x9 ) or 2(x4+x5+x10)
c. 3z(2z-5) or 3(2z2-5z) or z(6z-15)
d. 7w(6w2-2+11w4) or w(42w2-14+77w4)
e. z2 ((a+b)+z(a+b)) or z(z(a+b)+z2(a+b))
f. \(\frac{1}{2}\)(3s2+1)
g. 3p2 r2 (5pr2-2r3+3p2+\(\sqrt{2}\) pr4 ) or p2 r2 (15pr2-6r3+9p2+3\(\sqrt{2}\) pr4)
h. 0.4x8 (x-100) or \(\frac{4}{10}\) x8 (x-100)
i. (x2+x3 )((4x+3)-(2x+2))
j. (z-2)((2z+5)-13(z-3))
Choose one (or more) to go through as a class, listing as many different rewrites as possible. Then remark:
→ The process of making use of the distributive property “backward” is factoring.
Exercise 4.
Sammy wrote a polynomial using only one variable, x, of degree 3. Myisha wrote a polynomial in the same variable of degree 5. What can you say about the degree of the product of Sammy’s and Myisha’s polynomials?
Answer:
The degree of the product of the two polynomials would be 8.
Extension
Find a polynomial that, when multiplied by 2x2+3x+1, gives the answer 2x3+x2-2x-1.
Answer:
x-1
Eureka Math Algebra 1 Module 1 Lesson 9 Problem Set Answer Key
Question 1.
Use the distributive property to write each of the following expressions as the sum of monomials.
a. 3a(4+a)
Answer:
3a2+12a
b. x(x+2)+1
Answer:
x2+2x+1
c. \(\frac{1}{3}\)](12z+18z2)
Answer:
6z2+4z
d. 4x(x3-10)
Answer:
4x4-40x
e. (x-4)(x+5)
Answer:
x2+x-20
f. (2z-1)(3z2+1)
Answer:
6z3-3z2+2z-1
g. (10w-1)(10w+1)
Answer:
100w2-1
h. (-5w-3) w2
Answer:
-5w3-3w2
i. 16s100(\(\frac{1}{2}\) s200 + 0.125s)
Answer:
8s300+2s101
j. (2q+1)(2q2+1)
Answer:
4q3+2q2+2q+1
k. (x2-x+1)(x-1)
Answer:
x3-2x2+2x-1
i. 3xz(9xy+z)-2yz(x+y-z)
Answer:
27x2 yz+3xz2-2xyz-2y2 z+2yz2
m. (t-1)(t+1)(t2+1)
Answer:
t4-1
n. (w+1)(w4-w3+w2-w+1)
Answer:
w5+1
o. z(2z+1)(3z-2)
Answer:
6z3-z2-2z
p. (x+y)(y+z)(z+x)
Answer:
2xyz+x2 y+x2 z+xy2+xz2+y2 z+yz2
q. \(\frac{x+y}{3}\)
Answer:
\(\frac{1}{3}\) x+\(\frac{1}{3}\) y
r. (20f10-10f5)÷5
Answer:
4f10-2f5
s. -5y(y2+y-2)-2(2-y3)
Answer:
-3y3-5y2+10y
-4
t. \(\frac{(a+b-c)(a+b+c)}{17}\)
Answer:
\(\frac{1}{17}\) a2+\(\frac{1}{17}\) b2–\(\frac{1}{17}\) c2+2/17 ab
u. (2x÷9+(5x)÷2)÷(-2)
Answer:
–\(\frac{49 x}{36}\)
v. (-2f3-2f+1)(f2-f+2)
Answer:
-2f5+2f4-6f3+3f2-5f+2
Question 2.
Use the distributive property (and your wits!) to write each of the following expressions as a sum of monomials. If the resulting polynomial is in one variable, write the polynomial in standard form.
a. (a+b)2
Answer:
a2+2ab+b2
b. (a+1)2
Answer:
a2+2a+1
c. (3+b)2
Answer:
b2+6b+9
d. (3+1)2
Answer:
16
e. (x+y+z)2
Answer:
x2+y2+z2+2xy+2xz+2yz
f. (x+1+z)2
Answer:
x2+z2+2xz+2x+2z+1
g. (3+z)2
Answer:
z2+6z+9
h. (p+q)3
Answer:
p3+3p2 q+3pq2+q3
i. (p-1)3
Answer:
p3-3p2+3p-1
j. (5+q)3
Answer:
q3+15q2+75q+125
Question 3.
Use the distributive property (and your wits!) to write each of the following expressions as a polynomial in standard form.
a. (s2+4)(s-1)
Answer:
s3-s2+4s-4
b. 3(s2+4)(s-1)
Answer:
3s3-3s2+12s-12
c. s(s2+4)(s-1)
Answer:
s4-s3+4s2-4s
d. (s+1)(s2+4)(s-1)
Answer:
s4+3s2-4
e. (u-1)(u5+u4+u3+u2+u+1)
Answer:
u6-1
f. \(\sqrt{5}\)(u-1)(u5+u4+u3+u2+u+1)
Answer:
\(\sqrt{5}\)u6–\(\sqrt{5}\)
g. (u7+u3+1)(u-1)(u5+u4+u3+u2+u+1)
Answer:
u13+u9-u7+u6-u3-1
Question 4.
Beatrice writes down every expression that appears in this Problem Set, one after the other, linking them with + signs between them. She is left with one very large expression on her page. Is that expression a polynomial expression? That is, is it algebraically equivalent to a polynomial?
Answer:
Yes.
What if she wrote – signs between the expressions instead?
Answer:
Yes.
What if she wrote × signs between the expressions instead?
Answer:
Yes.
Eureka Math Algebra 1 Module 1 Lesson 9 Exit Ticket Answer Key
Question 1.
Must the product of three polynomials again be a polynomial?
Answer:
Yes.
Question 2.
Find (w2+1)(w3-w+1).
Answer:
w5+w2-w+1