Engage NY Eureka Math Algebra 1 Module 1 Lesson 7 Answer Key
Eureka Math Algebra 1 Module 1 Lesson 7 Exercise Answer Key
Exercise 1.
Suzy draws the following picture to represent the sum 3+4:
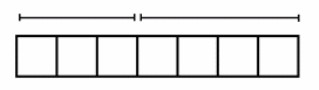
Ben looks at this picture from the opposite side of the table and says, “You drew 4+3.”
Explain why Ben might interpret the picture this way.
Answer:
Ben read the picture from his left to his right on his side of the table.
Exercise 2.
Suzy adds more to her picture and says, “The picture now represents (3+4)+2.”
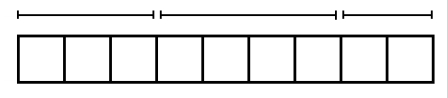
How might Ben interpret this picture? Explain your reasoning.
Answer:
Reading from right to left, the solution would be (2+4)+3. Make sure students have parentheses around 2+4.
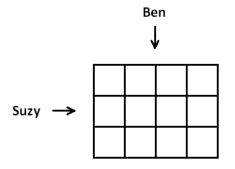
Exercise 3.
Suzy then draws another picture of squares to represent the product 3×4. Ben moves to the end of the table and says, “From my new seat, your picture looks like the product 4×3.”
What picture might Suzy have drawn? Why would Ben see it differently from his viewpoint?
Answer:
Squares should be arranged in a grid. If a student responds that Suzy made 3 rows of 4, then Ben’s viewpoint would be 4 rows of 3. Students should understand that Ben is seated to Suzy’s left or right now, not across from her. Some students may need scaffolding here—have them physically move to see the different viewpoint.
Exercise 4.
Draw a picture to represent the quantity (3×4)×5 that also could represent the quantity (4×5)×3 when seen from a different viewpoint.
Answer:
Student solutions could vary here. Students may consider representing the problem as a 3 by 4 by 5 rectangular box. When viewed from different faces, the different expressions appear. With the 3 by 4 rectangle viewed as its base, the volume of the box might be computed as (3×4)×5. But with the 4 by 5 rectangle viewed as its base, its volume would be computed as (4×5)×3. Some students will likely repeat the 3×4 pattern 5 times in a row. This diagram viewed from the end of the table would be 4 dots repeated 5 times arranged in 3 columns.
Ask students a series of questions of the following type:
→ Could the ideas developed in Exercises 1 and 2 be modified so as to explain why 2 \(\frac{1}{2}\)+\(\frac{3}{19}\) should equal
\(\frac{3}{19}\) +2 \(\frac{1}{2}\) ?
→ Or that ((-6562.65)+(-9980.77))+22 should equal (22+(-9980.77))+(-6562.65)?
→ How about that \(\sqrt{2}\)+\(\frac{1}{\pi}\) should equal \(\frac{1}{\pi}\)+\(\sqrt{2}\)?
→ Is it possible for a rectangle or a rectangular box to have a negative side length?
→ Could the ideas developed in Exercises 3 and 4 be used to show that (-3)×(\(\frac{1}{\sqrt{7}}\)) should equal (\(\frac{1}{\sqrt{7}}\))×(-3) or that (π×17.2)×(-\(\frac{16}{5}\) ) should equal ((-\(\frac{16}{5}\) )×17.2)×π?
Next, have students review the four properties of arithmetic provided in the student materials and ask the following:
Four Properties of Arithmetic:
THE COMMUTATIVE PROPERTY OF ADDITION: If a and b are real numbers, then a+b=b+a.
THE ASSOCIATIVE PROPERTY OF ADDITION: If a, b, and c are real numbers, then (a+b)+c=a+(b+c).
THE COMMUTATIVE PROPERTY OF MULTIPLICATION: If a and b are real numbers, then a×b=b×a.
THE ASSOCIATIVE PROPERTY OF MULTIPLICATION: If a, b, and c are real numbers, then (ab)c=a(bc).
→ Can you relate each of these properties to one of the previous exercises?
→ Exercise 1 connects with the commutative property of addition.
→ Exercise 2 connects with the associative property of addition. (Students might mention that the commutative property of addition is also relevant to this exercise. This will be discussed fully in
Exercise 5.)
→ Exercise 3 connects with the commutative property of multiplication.
→ Exercise 4 connects the associative property of multiplication. (Students might mention that the commutative property of multiplication is also relevant to this exercise. This will be discussed fully in Exercise 6.)
Point out that the four opening exercises suggest that the commutative and associative properties of addition and multiplication are valid for whole numbers and probably apply to all real numbers as well. However, there is a weakness in the geometric models since negative side lengths and areas are not meaningful. We choose to believe these properties hold for all real numbers, including negative numbers.
Exercise 5.
Viewing the diagram below from two different perspectives illustrates that (3+4)+2 equals 2+(4+3).
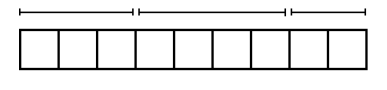
Is it true for all real numbers x, y, and z that (x+y)+z should equal (z+y)+x?
(Note: The direct application of the associative property of addition only gives (x+y)+z=x+(y+z).)
To answer this exercise with the class, create a flow diagram on the board as follows. This flow diagram will show how one can apply both the commutative and associative properties to prove the equivalence of these two expressions. Have students copy this work into their handouts.
Start by showing the application of each property on the expression (x+y)+z.
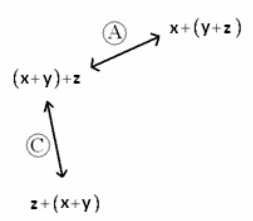
Here A represents an application of the associative property and C an application of the commutative property. Be sure students understand the application of the commutative property shown here.
Point out that we can extend this diagram by applying the commutative and associative properties to the new expressions in the diagram.
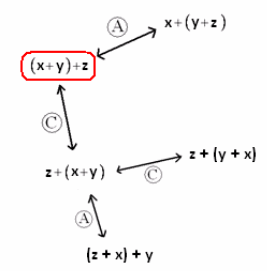
Note that there are multiple branches and options for extending this diagram. Direct the students to discover options that will chart a path from (x+y)+z to (z+y)+x. Two possible paths are as follows:
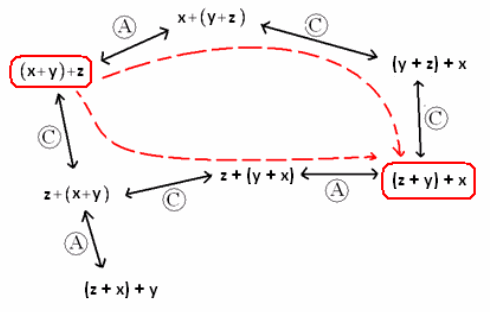
Choose one of the paths in the flow diagram and show on the board how to write it as a mathematical proof of the statement that (x+y)+z and (z+y)+x are equivalent expressions. For example, for the lower of the two paths shown, write the following:
(x+y)+z =z+(x+y) commutative property
=z+(y+x) commutative property
=(z+y)+x associative property
Exercise 6.
Draw a flow diagram and use it to prove that (xy)z=(zy)x for all real numbers x, y, and z.
Here is the start of the diagram.
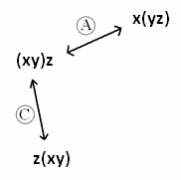
Students will likely realize the answer here is completely analogous to the solution to the previous exercise.
(xy)z =z(xy) commutative property
=z(yx) commutative property
=(zy)x associative property
Have students complete Exercises 7 and 8.
Exercise 7.
Use these abbreviations for the properties of real numbers, and complete the flow diagram.
C+ for the commutative property of addition
C× for the commutative property of multiplication
A+ for the associative property of addition
A× for the associative property of multiplication
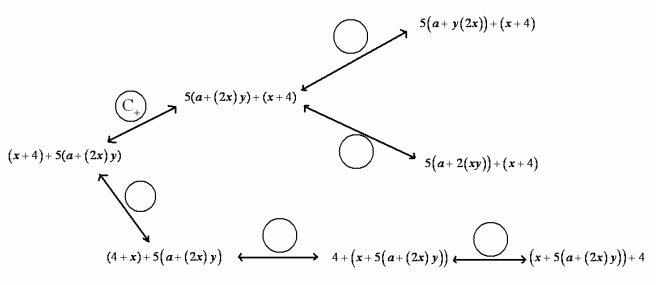
Answer:
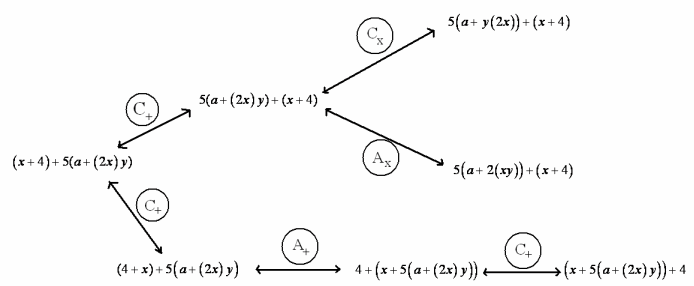
Exercise 8.
Let a, b, c, and d be real numbers. Fill in the missing term of the following diagram to show that ((a+b)+c)+d is sure to equal a+(b+(c+d)).

Answer:

→ This example illustrates that it is possible to prove, through repeated use of the associative property, that any two arrangements of parentheses around a given sum are equivalent expressions. For this reason it is deemed unnecessary to place parentheses among a sum of terms. (Present the following on the board.)
((a+b)+c)+d
a+(b+(c+d)) → a+b+c+d (a+b)+(c+d)
→ From now on, we will accept this as common practice. In presenting a proof, writing the following:
(x+(y+z)+(w+6))=((x+y)+(z+w)+6) by the associative property
OR
a+b+c+d=a+(b+c)+d by the associative property
for instance, is accepted.
The same holds for a product of symbols. Repeated application of the associative property of multiplication establishes the equivalency of ((xy)z)w and x((yz)w), for example, and these can both be written simply as xyzw.
Eureka Math Algebra 1 Module 1 Lesson 7 Problem Set Answer Key
Question 1.
The following portion of a flow diagram shows that the expression ab+cd is equivalent to the expression dc+ba.
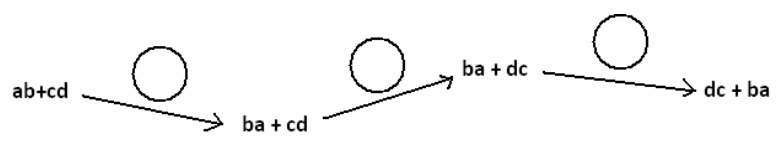
Fill in each circle with the appropriate symbol: Either C+ (for the commutative property of addition) or C× (for the commutative property of multiplication).
Answer:

Question 2.
Fill in the blanks of this proof showing that (w+5)(w+2) is equivalent to w2 +7w+10. Write either commutative property, associative property, or distributive property in each blank.
(w+5)(w+2) =(w+5)w+(w+5)×2 _____________
Answer:
distributive property
=w(w+5)+(w+5)×2 _____
Answer:
commutative property
=w(w+5)+2(w+5) _____________
Answer:
commutative property
=w2 +w×5+2(w+5) _____
Answer:
distributive property
=w2 +5w+2(w+5) _____
Answer:
commutative property
=w2 +5w+2w+10 _____
Answer:
distributive property
=w2 +(5w+2w)+10 _____
Answer:
associative property
=w2 +7w+10
Question 3.
Fill in each circle of the following flow diagram with one of the letters: C for commutative property (for either addition or multiplication), A for associative property (for either addition or multiplication), or D for distributive property.
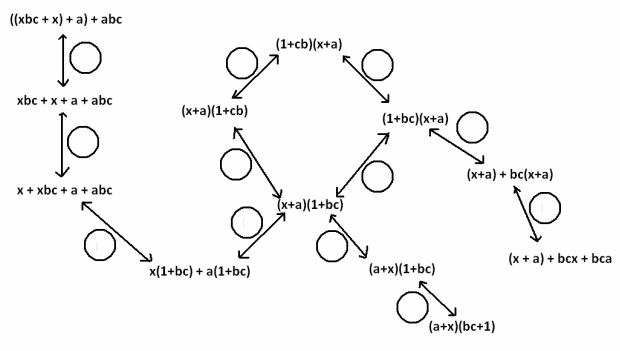
Answer:
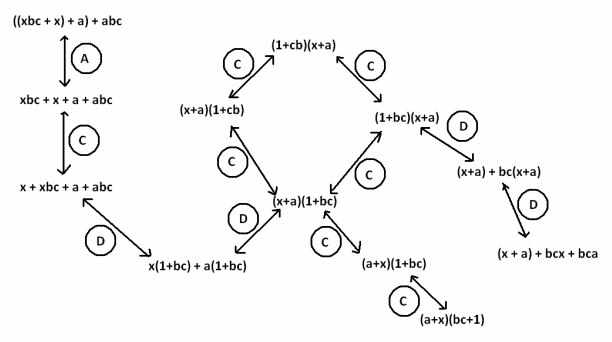
Question 4.
What is a quick way to see that the value of the sum 53+18+47+82 is 200?
Answer:
53+18+47+82=(53+47)+(18+82)=100+100
Question 5.
a. If ab=37 and y=\(\frac{1}{37}\), what is the value of the product x×b×y×a?
Answer:
x×b×y×a=(xy)(ab)=1
b. Give some indication as to how you used the commutative and associative properties of multiplication to evaluate x×b×y×a in part (a).
Answer:
x×b×y×a=x×y×a×b by two applications of the commutative property of multiplication and
x×y×a×b=(xy)(ab) by the associative property of multiplication.
c. Did you use the associative and commutative properties of addition to answer Problem 4?
Answer:
Yes, they were used in an analogous manner.
Question 6.
The following is a proof of the algebraic equivalency of (2x)3 and 8x3 . Fill in each of the blanks with either the statement commutative property or associative property.
(2x)3 = 2x∙2x∙2x
=2(x×2)(x×2)x ____
Answer:
associative property
=2(2x)(2x)x ___
Answer:
commutative property
=2∙2(x×2)x∙x ___
Answer:
associative property
=2∙2(2x)x∙x ___
Answer:
commutative property
=(2∙2∙2)(x∙x∙x) ____
Answer:
associative property
=8x3
Question 7.
Write a mathematical proof of the algebraic equivalency of (ab)2 and a2 b2 .
Answer:
(ab)2 =(ab)(ab)
=a(ba)b associative property
=a(ab)b commutative property
=(aa)(bb) associative property
=a2 b2
Question 8.
Suppose we are to play the 4-number game with the symbols a, b, c, and d to represent numbers, each used at most once, combined by the operation of addition ONLY. If we acknowledge that parentheses are unneeded, show there are essentially only 15 expressions one can write.
Answer:
By also making use of the commutative property of addition, we have the expressions:
a, b, c, d, a+b, a+c, a+d, b+c, b+d, c+d,
a+b+c, a+b+d, a+c+d, b+c+d, a+b+c+d
b. How many answers are there for the multiplication ONLY version of this game?
Answer:
By analogous reasoning, there are only 15 expressions here too.
Question 9.
Write a mathematical proof to show that (x+a)(x+b) is equivalent to x2 +ax+bx+ab.
Answer:
(x+a)(x+b) =(x+a)x+(x+a)b (D)
=x(x+a)+b(x+a) (C)
=x2 +xa+bx+ba (D)
=x2 +ax+bx+ab (C)
Question 10.
Recall the following rules of exponents:
xa ∙xb =xa+b
\(\frac{x^{a}}{x^{b}}\) = xa-b
(xa)b =xab
(xy)a =xaya
(\(\frac{x}{y}\))a =\(\frac{x^{a}}{y^{a}}\)
Here x, y, a, and b are real numbers with x and y nonzero.
Replace each of the following expressions with an equivalent expression in which the variable of the expression appears only once with a positive number for its exponent. (For example, \(\frac{7}{b^{2}}\)∙b-4 is equivalent to \(\frac{7}{b^{6}}\).)
a. (16x2 )÷(16x5 )
Answer:
\(\frac{1}{x^{3}}\)
b. (2x)4 (2x)3
Answer:
128x7
c. (9z-2 ) ((3z)-1)-3
Answer:
\(\frac{z}{3}\)
d. ((25w4 )÷(5w3 ))÷(5w-7)
Answer:
w8
e. (25w4 )÷((5w3 )÷(5w-7 ))
Answer:
\(\frac{25}{w^{6}}\)
Optional Challenge:
Question 11.
Grizelda has invented a new operation that she calls the average operator. For any two real numbers a and b, she declares a ![]() b to be the average of a and b:
b to be the average of a and b:
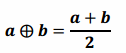
a. Does the average operator satisfy a commutative property? That is, does a ![]() b=b
b=b ![]() a for all real numbers a and b?
a for all real numbers a and b?
Answer:
Yes, use the fact that \(\frac{x}{2}\)=\(\frac{1}{2}\) ∙x for any real number x and the commutative property.
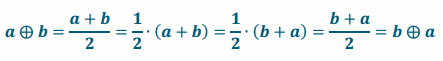
b. Does the average operator distribute over addition? That is, does a ![]() (b+c)=(a
(b+c)=(a ![]() b)+(a
b)+(a ![]() c) for all real numbers a, b, and c?
c) for all real numbers a, b, and c?
Answer:
No. For instance, 2 ![]() (4+4)=2
(4+4)=2![]() 8=5, whereas (2
8=5, whereas (2 ![]() 4)+(2
4)+(2 ![]() 4)=3+3=6.
4)=3+3=6.
Eureka Math Algebra 1 Module 1 Lesson 7 Exit Ticket Answer Key
Write a mathematical proof of the algebraic equivalence of (pq)r and (qr)p.
Answer:
(pq)r=p(qr) associative property
=(qr)p commutative property