Engage NY Eureka Math Algebra 1 Module 1 Lesson 27 Answer Key
Eureka Math Algebra 1 Module 1 Lesson 27 Example Answer Key
Example
Review Exercise 3 from the previous lesson: Using a generic initial value, a0, and the recurrence relation, ai+1=2ai+5, for i≥0, find a formula for a1, a2, a3, a4 in terms of a0.
Answer:
a1=2a0+5,
a2=2a1+5=2(2a0+5)+5=22∙a0+15,
a3=2a2+5=2(2∙2a0+15)+5=23∙a0+35,
a4=2a3+5=2(23∙a0+35)+5=24∙a0+75.
Eureka Math Algebra 1 Module 1 Lesson 27 Exercise Answer Key
Mathematical Modeling Exercise/Exercise 1
Using one of the four formulas from Example 1, write an inequality that, if solved for a0, will lead to finding the smallest starting whole number for the double and add 5 game that produces a result of 1,000 or greater in 3 rounds or fewer.
This exercise is loaded with phrases that students will need to interpret correctly in order to formulate an equation (do not expect this to be easy for them). Start with simple questions and build up:
→ What does a2 mean in terms of rounds?
→ The result of round two
→ Write what the statement, “produce a result of 1,000 or greater in two rounds,” means using a term of the sequence.
→ The result of round two, a2, must be greater than or equal to 1,000. Ask students to write the equation, a2≥1000, for that statement.
→ After replacing a2 in the inequality, a2≥1000, with the expression in terms of a0, what do the numbers a0 that satisfy the inequality, 4a0+15≥1000, mean?
→ The numbers a0 that satisfy the inequality are the starting numbers for the double and add 5 game that produce a result of 1,000 or greater in two rounds or fewer. The “or fewer” in the previous sentence is important and can be understood by thinking about the question, “Do we need two rounds to reach 1,000, starting with number 999? 800? 500?”
Let students solve for a0 in 4a0+15≥1000, and let them find the smallest whole number a0 for exactly two rounds (Answer: 247). Then continue with your questioning:
→ What inequality in terms of a0 would you write down to find the smallest starting number for the double and add 5 game that produces a result of 1,000 or greater in three rounds or fewer?
→ 8a0+35≥1000
Exercise 2.
Solve the inequality derived in Exercise 1. Interpret your answer, and validate that it is the solution to the problem. That is, show that the whole number you found results in 1,000 or greater in three rounds, but the previous whole number takes four rounds to reach 1,000.
Answer:
8a0+35≥1000
8a0+35-35≥1000-35
8a0≥965
\(\frac{1}{8}\) (8a0 )≥\(\frac{1}{8}\) (965)
a0≥\(\frac{965}{8}\)
Students should write or say something similar to the following response: I interpret a0≥\(\frac{965}{8}\) or a0≥120.625 as the set of all starting numbers that reach 1,000 or greater in three rounds or fewer. Therefore, the smallest starting whole number is 121. To validate, I checked that starting with 121 results in 1,003 after three rounds, whereas 120 results in 995 after three rounds.
Exercise 3.
Find the smallest starting whole number for the double and add 5 game that produces a result of 1,000,000 or greater in four rounds or fewer.
Answer:
16∙a0+75≥1 000 000
16a0+75-75≥1 000 000-75
16a0≥999 925
\(\frac{1}{16}\) (16a0 )≥\(\frac{1}{16}\) (999 925)
a0≥\(\frac{999 925}{16}\)
Students should write or say something similar to the following response: I interpreted a0≥\(\frac{999 925}{16}\) or a0≥62495.3125 as the set of all starting numbers that reach 1,000,000 or greater in four rounds or fewer. Therefore, the smallest starting whole number is 62,496. To validate, I checked that starting with 62,496 results in 1,000,011 after four rounds, whereas 62,495 results in 999,995 after four rounds.
Eureka Math Algebra 1 Module 1 Lesson 27 Problem Set Answer Key
Question 1.
Your older sibling came home from college for the weekend and showed you the following sequences (from her homework) that she claimed were generated from initial values and recurrence relations. For each sequence, find an initial value and recurrence relation that describes the sequence. (Your sister showed you an answer to the first problem.)
a. (0,2,4,6,8,10,12,14,16,…)
Answer:
a1=0 and ai+1=ai+2 for i≥1
b. (1,3,5,7,9,11,13,15,17,…)
Answer:
a1=1 and ai+1=ai+2 for i≥1
c. (14,16,18,20,22,24,26,…)
Answer:
a1=14 and ai+1=ai+2 for i≥1
d. (14,21,28,35,42,49,…)
Answer:
a1=14 and ai+1=ai+7 for i≥1
e. (14,7,0,-7,-14,-21,-28,-35,…)
Answer:
a1=14 and ai+1=ai-7 for i≥1
f. (2,4,8,16,32,64,128,…)
Answer:
a1=2 and ai+1=2ai for i≥1
g. (3,6,12,24,48,96,…)
Answer:
a1=3 and ai+1=2ai for i≥1
h. (1,3,9,27,81,243,…)
Answer:
a1=1 and ai+1=3ai for i≥1
i. (9,27,81,243,…)
Answer:
a1=9 and ai+1=3ai for i≥1
Question 2.
Answer the following questions about the recursive sequence generated by initial value, a1=4, and recurrence relation, ai+1=4ai for i≥1.
a. Find a formula for a1, a2, a3, a4, a5 in terms of powers of 4.
Answer:
a1=41
a2=42
a3=43
a4=44
a5=45
b. Your friend, Carl, says that he can describe the nth term of the sequence using the formula, a_n=4n. Is Carl correct? Write one or two sentences using the recurrence relation to explain why or why not.
Answer:
Yes. The recurrence relation, ai+1=4ai for i≥0, means that the next term in the sequence is always 4 times larger than the current term, i.e., one more power of 4. Therefore, the nth term will be n powers of 4, or 4n.
Question 3.
The expression, 2n (a0+5)-5, describes the nth term of the double and add 5 game in terms of the starting number a0 and n. Verify that it does describe the nth term by filling out the tables below for parts (b) through (e). (The first table is done for you.)
a. Table for a0=1
Answer:
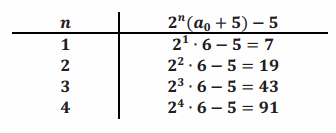
b. Table for a0=8
Answer:
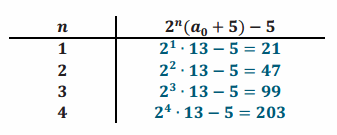
c. Table for a0=9
Answer:
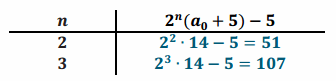
d. Table for a0=120
Answer:
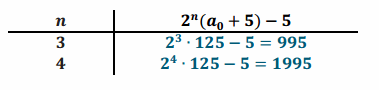
e. Table for a0=121
Answer:
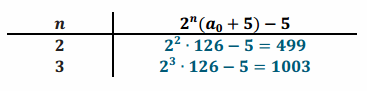
Question 4.
Bilbo Baggins stated to Samwise Gamgee, “Today, Sam, I will give you $1. Every day thereafter for the next 14 days, I will take the previous day’s amount, double it and add $5, and give that new amount to you for that day.”
a. How much did Bilbo give Sam on day 15? (Hint: You don’t have to compute each term.)
Answer:
a15=215 (1+5)-5=196,603. Bilbo gave Sam $196,603 on day 15.
b. Did Bilbo give Sam more than $350,000 altogether?
Answer:
Yes. He gave $98,299 on day 14, $49,147, on day 13, $24,571 on day 12, and so on.
Question 5.
The formula, an=2n-1 (a0+5)-5, describes the nth term of the double and add 5 game in terms of the starting number a0 and n. Use this formula to find the smallest starting whole number for the double and add 5 game that produces a result of 10,000,000 or greater in 15 rounds or fewer.
Answer:
Solving 214 (a0+5)-5≥10 000 000 for a0 results in a0≥300.1759….
Hence, 301 is the smallest starting whole number that will reach 10,000,000 in 15 rounds or fewer.
Eureka Math Algebra 1 Module 1 Lesson 27 Exit Ticket Answer Key
Write a brief report about the answers you found to the double and add 5 game problems. Include justifications for why your starting numbers are correct.
Results for finding the smallest starting number in the double and add 5 game:
1. Reaching 100 in three rounds or fewer: The starting number 9 results in 107 in round three. The starting number 8 results in 99 in round three, requiring another round to reach 100. Numbers 1–8 take more than three rounds to reach 100.
2. Reaching 1,000 in three rounds or fewer: The starting number 121 results in 1,003 in round three. The starting number 120 results in 995 in round three, requiring another round to reach 1,000. All other whole numbers less than 120 take more than three rounds to reach 1,000.
3. Reaching 1,000,000 in four rounds or fewer: The starting number 62,496 results in 1,000,011 in round four. The starting number 62,495 results in 999,995 in round four, requiring another round to reach 1,000,000. All other whole numbers less than 62,495 take more than four rounds to reach 1,000,000.