A cuboid is a three-dimensional shape having three axes. It has 3 faces which are convex polyhedrons, 12 edges, 12 vertices. Find the different formulas of the cuboid like perimeter, total surface area, lateral surface area, base surface area, and diagonal in the following sections of this page. One can also find the cuboid definition, properties, and solved example questions here.
Cuboid Definition
The cuboid is a closed three-dimensional geometric figure having 6 rectangular regions. Each rectangular region is called the face. The point of intersection of three edges in the cuboid is called the vertices or corners. The sides of all rectangular faces are called the edges of the cuboid. Some of the examples for the objects in the cuboid shape are matchbox, shoebox, bricks, matrices.
The shape of the cuboid is shown here.
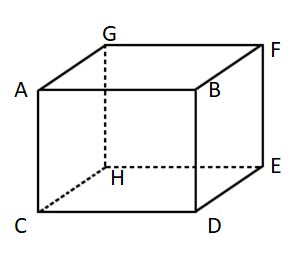
Faces, Edges, Vertices of the Cuboid
The cuboid is made up of 6 rectangular faces, 12 edges, 8 corners. The faces, edges, and corners for the above-mentioned cuboid image are as follows:
- The six faces are ABCD, BDEF, ABGF, AGCH, CDHE, EFGH.
- Eight corners or vertices are A, B, C, D, E, F, G, H.
- Twelve edges and opposite sides of the rectangle are AB = CD = EH = GF, AC = BD = EF = GH, DE = BF = CH = AG.
Cuboid Formulas
The cuboid formulas are provided-below. Get the total surface area, diagonal, perimeter, and volume of the cuboid. Let us consider l, b, h are the length, breadth, and height of the cuboid respectively.
Cuboid Surface Area
The surface area is nothing but the total region covered by all the faces. Generally, the cuboid surface area is classified into two types they are lateral surface area and total surface area. It is also defined as the sum of areas of six faces of the cuboid.
Lateral Surface Area
The lateral surface area is the sum of the areas of all faces except the top and bottom faces.
Cuboid Lateral Surface Area = (Area of ABCD + Area of BDEF + Area of EFGH + Area of AGCH)
= (b × h) + (b × h) + (l × h) + (l × h)
= 2h(l + b)
Total Surface Area
Cuboid Total Surface Area is the sum of the faces.
Total Surface Area of the Cuboid = (Area of ABCD + Area of BDEF + Area of EFGH + Area of AGCH + Area of ABGF + Area of CDHE)
= (l × b) + (l × b) + (b × h) + (b × h) + (l × h) + (l × h)
= 2lb + 2bh + 2hl
= 2(lb + bh + lh)
Cuboid Diagonal
The length of the diagonal of a cuboid is along the lines.
Diagonal = √(l² + b² + h²)
Cuboid Perimeter
The perimeter is the sum of the edges of all edges.
The perimeter of the Cuboid = AB + BF + FE + BD + DE + CD + CH + AC + GH + AG + GF + HE
= l + l + l + l + b + b + b + b + h + h + h + h
= 4(l + b + h)
Cuboid Volume
Cuboid volume is the product of the base area and height.
Volume = length x breadth x height
= lbh
Read More Related Articles:
Properties of Cuboid
Here is the list of Properties of Cuboids such as faces, edges, vertices, angles, etc. They are as follows
- A cuboid has 6 faces, twelve edges, and 8 vertices.
- It has rectangular-shaped faces.
- The angles are plane and at a right angle.
- Opposite edges are parallel to each other.
Solved Examples on Cuboid
Example 1:
Calculate the volume, diagonal, surface area, and perimeter of the cuboid, if the cuboid length is 8 cm, width is 5 cm, and height is 10 cm.
Solution:
Given that,
Cuboid length l = 8 cm
breadth b = 5 cm
height h = 10 cm
Cuboid volume v = lbh
= 8 x 5 x 10
= 400 cm³
Diagonal of the cuboid = √(l² + b² + h²)
= √(8² + 5² + 10²)
= √(64 + 25 + 100)
= √(189)
= 3√(21) cm
Perimeter = 4(l + b +h)
= 4(8 + 5 + 10)
= 4(23)
= 92 cm
Total Surface Area = 2(lb + bh + lh)
= 2(8 x 5 + 5 x 10 + 8 x 10)
= 2(40 + 50 +80)
= 2(170)
= 340 cm²
∴ Perimeter, diagonal, total surface area, and volume of the cuboid are 92 cm, 3√(21) cm, 340 cm² & 400 cm³.
Example 2:
The lunchbox measures 20 cm long, 10 cm wide, and 5 cm high. what is the total surface area, the lateral surface area of the box?
Solution:
Given that,
Lunchbox length l = 20 cm
Width b = 10 cm
Height h = 5 cm
Total Surface Area of the lunchbox = 2(lb + bh + lh)
= 2(20 x 10 + 10 x 5 + 20 x 5)
= 2(200 + 50 + 100)
= 2(350)
= 700 cm²
Lateral Surface Area of the lunchbox = 2h(l + b)
= 2 x 5(20 + 10)
= 10(30)
= 300 cm²
∴ The total surface area of the lunchbox is 700 cm², lateral surface area is 300 cm².
Example 3:
If the cuboid volume is ∛(126) m³, breadth is 2 m and height is 3 m. Find its length?
Solution:
Given that,
The volume of the cuboid = ∛(126) m³
lbh = ∛(126) m³
l x 2 x 3 = ∛(126)
l x 6 = ∛(126)
l = ∛(126) / 6
l = 21 m
∴ The cuboid length is 21 m.
Example 4:
If the volume of a room is 792 m³ and the area of the floor is 132 m², find the height of the room.
Solution:
Given that,
The volume of a room = 792 m³
Area of the floor = 132 m²
Height of the room = Volume of a room / Area of the floor
= 792/132
= 6 m
Therefore, the height of the room is 6 m.
