Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 3 Module 4 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Student Book Answer Key Unit 3 Module 4
Bridges in Mathematics Grade 5 Student Book Unit 3 Module 4 Session 1 Answer Key
Rounding & Division Practice
Question 1.
Complete each sentence below.
a. If you want to round a number to the nearest ten, you need to look at the number in the ______________ place.
Answer: If you want to round a number to the nearest ten, you need to look at the number in the Ones place.
b. If you want to round a number to the nearest hundred, you need to look at the number in the ______________ place.
Answer: If you want to round a number to the nearest hundred, you need to look at the number in the tens place.
Question 2.
Round each number first to the nearest ten and then to the nearest hundred.
ex:
Number: 382
Nearest Ten: 380
Nearest Hundred: 400
a. Number: 437
Nearest Ten: _______________
Nearest Hundred: _____________
Answer:
To round to the nearest tens, we mark the digits in the ones and tens column.
437 to the nearest ten is 440.
When rounding to the nearest hundred, look at the TENS DIGIT of the number. If that digit is 0, 1, 2, 3, or 4, you will round down to the previous hundred. If that digit is 5, 6, 7, 8, or 9, you will round up to the next hundred.
437 to the nearest hundred is 400.
b Number: 264
Nearest Ten: _______________
Nearest Hundred: _____________
Answer:
264 to the nearest ten is 260.
To round to the nearest tens, we mark the digits in the ones and tens column.
When rounding to the nearest hundred, look at the TENS DIGIT of the number. If that digit is 0, 1, 2, 3, or 4, you will round down to the previous hundred. If that digit is 5, 6, 7, 8, or 9, you will round up to the next hundred.
264 to the nearest hundred is 300.
c. Number: 578
Nearest Ten: _______________
Nearest Hundred: _____________
Answer:
578 to the nearest ten is 580.
To round to the nearest tens, we mark the digits in the ones and tens column.
When rounding to the nearest hundred, look at the TENS DIGIT of the number. If that digit is 0, 1, 2, 3, or 4, you will round down to the previous hundred. If that digit is 5, 6, 7, 8, or 9, you will round up to the next hundred.
578 to the nearest hundred is 600.
d. Number: 843
Nearest Ten: _______________
Nearest Hundred: _____________
Answer:
843 to the nearest ten is 840.
To round to the nearest tens, we mark the digits in the ones and tens column.
When rounding to the nearest hundred, look at the TENS DIGIT of the number. If that digit is 0, 1, 2, 3, or 4, you will round down to the previous hundred. If that digit is 5, 6, 7, 8, or 9, you will round up to the next hundred.
843 to the nearest hundred is 800.
e. Number: 235
Nearest Ten: _______________
Nearest Hundred: _____________
Answer:
235 to the nearest ten is 230.
To round to the nearest tens, we mark the digits in the ones and tens column.
When rounding to the nearest hundred, look at the TENS DIGIT of the number. If that digit is 0, 1, 2, 3, or 4, you will round down to the previous hundred. If that digit is 5, 6, 7, 8, or 9, you will round up to the next hundred.
235 to the nearest hundred is 200.
Question 3.
Complete the division problems.
12 ÷ 2 = _____________
24 ÷ 6 = _____________
18 ÷ 3 = ______________
45 ÷ 5 = ______________
120 ÷ 2 = ______________
240 ÷ 6 = ______________
180 ÷ 3 = _______________
450 ÷ 5 = ______________
Answer:
12 ÷ 2 = 6
12/2 = 6
By dividing 12 by 2 we get 6.
24 ÷ 6 = 4
By dividing 24 by 6 we get 4.
18 ÷ 3 = 6
By dividing 18 by 3 we get 6.
45 ÷ 5 = 9
By dividing 45 by 5 we get 9.
120 ÷ 2 = 60
By dividing 120 by 2 we get 60.
240 ÷ 6 = 40
By dividing 240 by 6 we get 40
180 ÷ 3 = 60
By dividing 180 by 3 we get 60.
450 ÷ 5 = 90
By dividing 450 by 5 we get 90.
Question 4.
Round to the nearest 10 and then divide to estimate each quotient.
ex:
Problem: 123 ÷ 2
Rounded: 120 ÷ 2 = 60
Estimated Quotient: 123 ÷ 2 is about equal to _____________.
Answer:
123 ÷ 2 = 61.5
61.5 to the nearest 10 is 60.
120 ÷ 2 = 60
Estimated Quotient: 123 ÷ 2 is about equal to 60
a. Problem: 177 ÷ 3
Rounded: ____________
Estimated Quotient: 177 ÷ 3 is about equal to _____________.
Answer:
177 ÷ 3 = 59
59 to the nearest 10 is 60.
Estimated Quotient: 177 ÷ 3 is about equal to 60.
b. Problem: 237 ÷ 6
Rounded: ____________
Estimated Quotient: 237 ÷ 6 is about equal to _____________.
Answer:
237 ÷ 6 = 39.5
39.5 to the nearest 10 is 40.
Estimated Quotient: 237 ÷ 6 is about equal to 40.
c. Problem: 452 ÷ 5
Rounded: ____________
Estimated Quotient: 452 ÷ 5 is about equal to _____________.
Answer:
452 ÷ 5 = 90.4
90.4 to the nearest 10 is 90.
Estimated Quotient: 452 ÷ 5 is about equal to 90.
Bridges in Mathematics Grade 5 Student Book Unit 3 Module 4 Session 2 Answer Key
Base Ten Grid Paper


Division Practice
Question 1.
Choose one division problem below and circle it. Pick the one that seems best for you—not too hard and not too easy.
180 ÷ 12
220 ÷ 20
440 ÷ 22
520 ÷ 26
a. Write a story problem to match the division problem you just circled.
Answer:
b. Make a labeled sketch on the grid below to show the problem you chose.
Answer:
c. Find the answer to the problem you chose using your sketch. Show all your work.

Answer:
Bridges in Mathematics Grade 5 Student Book Unit 3 Module 4 Session 3 Answer Key
Work Place Instructions 3E Division Showdown
Each pair of players needs
- a 3E Division Showdown Starter Sheet (Regular or Challenge Version) to share
- a 3E Division Showdown Continuation Sheet A to share
- a 3E Division Showdown Continuation Sheet B to share
- 1 spinner overlay
- 1 red and 1 blue colored pencil or markers
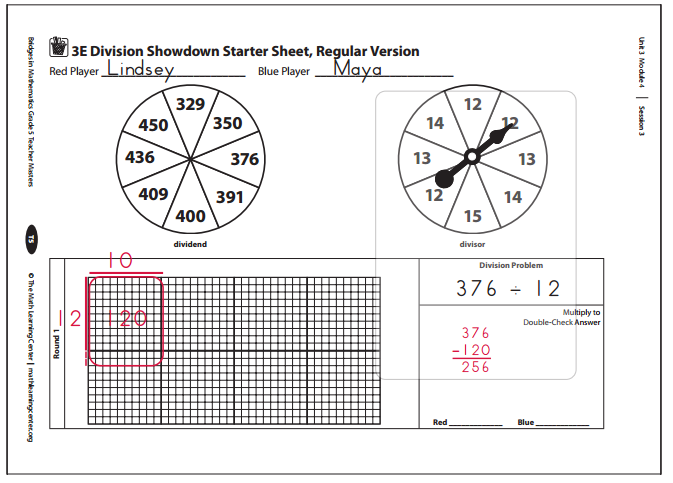
1. Players record their names at the top of the starter sheet, then decide which player will go first and what color each player will use.
2. Player 1 spins the spinners and records a division problem using the two numbers. Then he marks and labels the known dimension (the divisor) on the grid with his or her color.
3. Next, Player 1 loops and labels 10 times the divisor, and records the results in the figuring box to the right of the grid, working in his or her own color.
For example, if the divisor spun was 12, loop and label 12 × 10 on the grid, then mark it by drawing the dimension across the top. Work in the figuring box to subtract 120 from the dividend to see how much is still left.
Lindsey OK, I’m first. I spun 376 and 12, so now I have to write 376 ÷ 12 in the division problem box. Then I have to mark 12 on the side of the grid, and loop and label 10 × 12, which is 120. The last thing I have to do is subtract 120 from 376 so we can see how much we still have. It’s 256, and it’s your turn now, Maya.
4. Player 2 takes a turn to loop and label 10 times the divisor using his or her own color, and record the results in the figuring box.
5. Players take turns looping and labeling 10 times the divisor and recording the results in the figuring box until there isn’t enough left of the dividend to subtract 10 times the divisor again.
6. When there isn’t enough left to subtract 10 times the divisor anymore, the player whose turn it is gets to subtract as many groups of the divisor as he or she wants.
The player should try to remove as many groups as possible, since the player who makes the last removal wins the round.
7. The player who makes the last move must do the following:
- Loop and label the final groups on the grid.
- Subtract the final amount in the figuring box.
- Show the remainder, if there is one, with Xs on the grid.
- Write the answer to the division problem.
- Multiply the quotient times the divisor, and add the remainder if there is one, to double-check the answer.
8. The player who makes the last move scores points equal to the remainder, if there is one. If there is no remainder he scores 1 point for being the last to make a move.
Before the winner of the round can take the points, the other player gets to add up the pieces, including the remainder, on the grid to be sure they total the dividend. If they don’t, both players have to find the mistake and fix it.
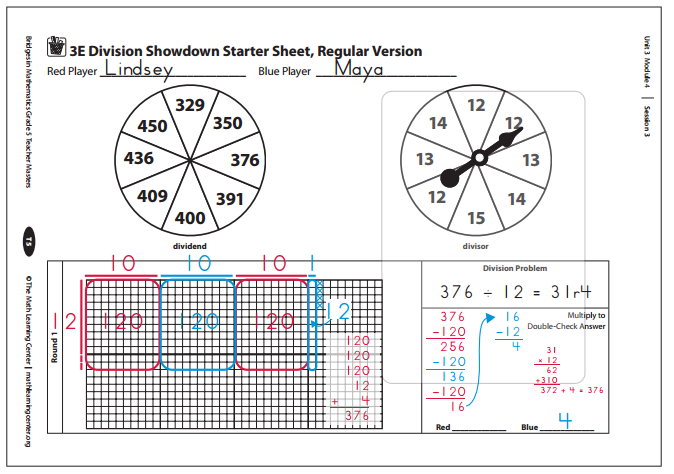
9. Players play four more rounds (using 3E Division Showdown Continuation Sheets A & B to record the results), then find the sum of their points from all 5 rounds to see who wins the game. (High score wins.) Players should take turns starting first. If the red player started Round 1, the blue player should start Round 2, and they should continue to alternate starting each new round.
Game Variations
A. Use the Challenge Version of the Starter Sheet, which has higher dividends and divisors.
Answer:
Metric Conversions
Knowing how to multiply and divide by 10, 100, and 1,000 can help you make conversions between units in the metric system.
Question 1.
Metric Units of Length/Distance
a. Complete the following sentences.
There are ____________ millimeters in 1 meter.
There are ____________ centimeters in 1 meter.
There are ____________ meters in 1 kilometer.
Answer:
Convert from meter to millimeters, centimeters.
1 meter = 100 cm
1 meter = 1000 millimeter
1 kilometer = 1000 meter
There are 1000 millimeters in 1 meter.
There are 100 centimeter in 1 meter.
There are 1000 meters in 1 kilometer.
b. Use the information in part a to complete the equivalencies below.
____________ millimeters = 1 centimeter
____________ centimeters = 1 kilometer
____________ millimeters = 1 kilometer
Answer:
Convert from cm to mm
1 centimeter = 10 millimeter
Convert from kilometer to centimeter and millimeters
1 kilometer = 1000000 millimeter
1 kilometer = 100000 centimeter
10 millimeters = 1 centimeter
100000 centimeters = 1 kilometer
1000000 millimeters = 1 kilometer
Question 2.
Metric Units of Volume/Capacity
a. Complete the following sentences.
There are ____________ milliliters in 1 liter.
There are ____________ centiliters in 1 liter.
There are ____________ liters in 1 kiloliter.
Answer:
Convert from liters to milliliters, centiliters and kiloliter to liters.
1 liter = 1000 milliliter
1 liter = 100 centiliter
1 kiloliter = 1000 liters
b. Use the information in part a to complete the equivalencies below.
____________ milliliters = 3 liters
____________ centiliters = 4 liters
____________ liters = 7 kiloliters
Answer:
Convert from liters to milliliters, centiliters and kiloliter to liters.
1 kiloliter = 1000 liters
7 kiloliters = 7 × 1000 liters = 7000 liters
1 liter = 100 centiliter
4 liters = 4 × 100 centiliter = 400 centiliter
1 liter = 1000 ml
3 liters = 3 × 1000 = 3000 milliliters
3 milliliters = 3 liters
400 centiliters = 4 liters
7000 liters = 7 kiloliters
Question 3.
Metric Units of Mass
a. Complete the following sentences.
There are ____________ milligrams in 1 gram.
There are ____________ centigrams in 1 gram.
There are ____________ grams in 1 kilogram.
Answer:
Convert from gram to milligrams, centigrams, and kilogram to gram.
1 gram = 1000 milligrams
1 gram = 100 cg
1 kilogram = 1000 grams
There are 1000 milligrams in 1 gram.
There are 100 centigrams in 1 gram.
There are 1000 grams in 1 kilogram.
b. Use the information in part a to complete the equivalencies below.
____________ milligrams = 2.5 grams
____________ centigrams = 4.5 grams
____________ grams = 3.5 kilograms
Answer:
1 gram = 1000 milligrams
2.5 grams = 2.5 × 1000 = 2500 milligrams
There are 100 centigrams in 1 gram.
4.5 grams = 4.5 × 100 = 450 centigrams
There are 1000 grams in 1 kilogram.
3.5 kg = 3.5 × 1000 = 3500 grams
Question 4.
CHALLENGE Complete the following conversions.
a. ____________ millimeters = 10 kilometer
Answer:
1 kilometer = 1000000 millimeter
10 kilometer = 10 × 1000000 = 10000000 millimeters
b. ____________ millimeters = 4.5 kilometers
Answer:
1 kilometer = 1000000 millimeter
4.5 kilometer = 4.5 × 1000000 = 4500000 millimeters
Bridges in Mathematics Grade 5 Student Book Unit 3 Module 4 Session 4 Answer Key
More Rounding & Estimation Practice
Question 1.
Complete the following multiplication and division fact families.
ex:
40 × 3 = 120
3 × 40 = 120
120 ÷ 40 = 3
120 ÷ 3 = 40
a. 30 × 5 = 150
Answer:
30 × 5 = 150
5 × 30 = 150
150 ÷ 30 = 5
150 ÷ 5 = 30
b. 20 × 6 = 120
Answer:
20 × 6 = 120
6 × 20 = 120
120 ÷ 6 = 20
120 ÷ 20 = 6
c. 40 × 7 = 280
Answer:
40 × 7 = 280
7 × 40 = 280
280 ÷ 7 = 40
280 ÷ 40 = 7
Question 2.
Use rounding and estimation to answer each question yes or no without doing all of the calculations.
a. Mrs. Jackson has 3 grandchildren who go to Park Heights Elementary School. At Back to School Night, she wanted to buy each of them 2 T-shirts with the school mascot on them. The T-shirts cost $18 each, and she has $150 to spend. Can she buy 2 T-shirts for each grandchild?
![]() Yes
Yes
![]() No
No
Answer:
Given,
Mrs. Jackson has 3 grandchildren who go to Park Heights Elementary School. At Back to School Night, she wanted to buy each of them 2 T-shirts with the school mascot on them.
The T-shirts cost $18 each
$18 × 2 = $36
$36 × 3 = $108
she has $150 to spend
Yes, she can buy 2 T-shirts for each grandchild.
b. It costs $27 per person to go to an amusement park. Mr. Lee is taking his two children to the amusement park, and he has $120 to spend. Can he afford for each of his children to bring a friend?
![]() Yes
Yes
![]() No
No
Answer:
It costs $27 per person to go to an amusement park.
Mr. Lee is taking his two children to the amusement park, and he has $120 to spend.
$27 × 3 = $81
So, Yes he can afford for each of his children to bring a friend.
c. Rachel is reading a book that is 293 pages long. If she reads 38 pages per night, will she be able to finish the book in a week?
![]() Yes
Yes
![]() No
No
Answer:
Given,
Rachel is reading a book that is 293 pages long.
she reads 38 pages per night
1 week = 7 days
38 × 7 = 266
No, she cannot finish the book in a week.
d. Dante’s cousin Carl was bragging that he biked 82 miles last week. If Dante bikes 18 miles a day for 5 days, will he ride more miles than Carl did?
![]() Yes
Yes
![]() No
No
Answer:
Given,
Dante’s cousin Carl was bragging that he biked 82 miles last week.
If Dante bikes 18 miles a day for 5 days.
18 × 5 = 90 miles
Yes, he can ride more than Carl.
Question 3.
CHALLENGE Bakery A sells boxes of 6 muffins for $5.85. Bakery B sells boxes of 8 muffins for $8.25. Which bakery offers the better deal on muffins? How can you tell?
Answer:
Given,
Bakery A sells boxes of 6 muffins for $5.85.
Bakery A sells boxes of 1 muffin for 5.85/6 = $0.975
Bakery B sells boxes of 8 muffins for $8.25.
Bakery B sells boxes of 1 muffin for $8.25/8 = $1.03
1.03 > 0.975
Bakery A offers better deal on muffins.