Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 1 Module 4 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Student Book Answer Key Unit 1 Module 4
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 4 Session 1 Answer Key
Multiplication & Division
Mathematical Thinking
Question 1.
Katie says she can multiply 5 × 68 by multiplying 10 × 68 and dividing the answer in half.
a. Do you agree or disagree? Explain your thinking.
Answer:
Yes, agreed.
Explanation:
multiply 5 × 68 by multiplying
5 × 68 = 340
10 × 68 and dividing the answer in half.
10 × 68 = 680
680 ÷2 = 340
b. Write an expression that shows Katie’s thinking. Use parentheses.
Answer:
5 × 68 = (10 × 68) ÷ 2
Explanation:
5 × 68 = 340
(10 × 68) ÷ 2 = 680 ÷ 2 = 340
Question 2.
Henry says he can multiply 99 × 57 by multiplying 100 × 57 and then adding one more 57.
a. Do you agree or disagree? Explain your thinking.
Answer:
disagree
Explanation:
Given that,
Henry says he can multiply 99 × 57 by multiplying 100 × 57 and then adding one more 57.
99 × 57 = 5,643
100 × 57 = 5,700 + 57 = 5,757
b. Write an expression that shows Henry’s thinking. Use parentheses.
Answer:
(99 × 57) = (100 × 57)+ 57
Explanation:
Henry says he can multiply 99 × 57 by multiplying 100 × 57 and then adding one more 57.
(99 × 57) ≠ (100 × 57)+ 57
Question 3.
Paris is packing a crate of flower pots. She puts 2 rows of 6 flowerpots in each layer of a box.
There are 2 layers in the box.
a. Write an expression that shows how many flowerpots are in the box.
Answer:
(2 × 6) × 2 = 24
Explanation:
She puts 2 rows of 6 flowerpots in each layer of a box.
(2 × 6)
There are 2 layers in the box.
12 × 2 = 24
b. Write an equation to show how many flowerpots are in the box.
Answer:
(2 × 6) × 2 = 24
Explanation:
Given that,
Paris is packing a crate of flower pots. She puts 2 rows of 6 flowerpots in each layer of a box.
There are 2 layers in the box.
(2 × 6) × 2 = 24
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 4 Session 2 Answer Key
Division Story Problems
For each problem on this page and the next,
- Write an equation, including parentheses if needed, to match the situation.
- Find the answer. You can use base ten pieces to model and solve the part of the problem that requires division.
- Label your answer with the correct units.
- Explain what you did with the remainder and why.
Question 1.
Josh and his three friends baked cookies last Saturday. When they were finished, they had 65 cookies. Each of the 4 friends ate 2 cookies right away and divided the rest equally to take home. How many cookies did each of the friends get to take home?
Answer:
14.25 cookies or 14 cookies.
Explanation:
Given that,
Josh and his three friends had 65 cookies.
Each of the 4 friends ate 2 cookies right away and divided the rest equally to take home.
Number of cookies did each of the friends get to take home,
65 – (4 × 2) ÷ 4
= 65 – 8 ÷ 4
= 57 ÷ 4
= 14.25
Question 2.
Sara and 5 of her friends did chores all Saturday and earned $75.00. Sara’s dad was so pleased with their work that he gave each of the 6 children a $2.00 tip in addition to the $75.00. They shared the work equally, so they want to share all the money equally. How much money will each person get?
Answer:
$14.5
Explanation:
Given that,
Sara and 5 of her friends did chores all Saturday and earned $75.00.
1 + 5 = $75
Sara’s dad was so pleased with their work and gave each of the 6 children a $2.00 tip in addition to the $75.00.
(6 × 2) + $75 = 12 + 75 = $87
Total money will each person get 87 ÷ 6 = $14.5
Question 3.
Mrs. O’Donnell is taking 36 fifth graders and 7 parent helpers on a field trip. She wants to give each person, including herself, 2 granola bars for snacks. If there are 5 granola bars in a box, how many boxes will she need to buy?
Answer:
18 boxes she need to buy.
Explanation:
Given that,
Mrs. O’Donnell is taking 36 fifth graders and 7 parent helpers on a field trip.
36 + 7 = 43
She wants to give each person, including herself, 2 granola bars for snacks.
(43 + 1) × 2 = 88
If there are 5 granola bars in a box,
88 ÷ 5 = 17.6 or 18
Therefore, 18 boxes she need to buy.
Question 4.
Eighty-nine kids showed up for the first soccer practice. The coaches organized them into groups of 4 for warm-up exercises. How many groups were there?
Answer:
22.25 or 22 groups.
Explanation:
Given that,
Eighty-nine kids showed up for the first soccer practice.
The coaches organized them into groups of 4 for warm-up exercises.
Number of groups were there = 89 ÷ 4 = 22.25 or 22
Question 5.
Jamal and three of his friends raked leaves every weekend for a month. By the end of the month, they earned $91.00. They paid $4.00 to Jamal’s little brother for helping out a little on the last day. Then the four friends divided the rest of the money equally. How much did each friend get?
Answer:
$21.75
Explanation:
Given that,
Jamal and three of his friends by the end of the month earned $91.00.
They paid $4.00 to Jamal’s little brother for helping out a little on the last day.
$91.00 – $4.00 = $87
Then the four friends divided the rest of the money equally.
Total amount did each friend get 87 ÷ 4 = $21.75
Question 6.
The drivers at Pizza Palace were loading up their 3 delivery vans for the evening. There were 65 pizzas. The boss told them to put an equal number of pizzas in each van and said they could split any leftovers equally. How much of a leftover pizza did each of the 3 drivers get?
Answer:
21 with 2 left over.
Explanation:
Given that,
The drivers at Pizza Palace were loading up their 3 delivery vans for the evening.
There were 65 pizzas.
Number of leftover pizza did each of the 3 drivers get 65 ÷ 3 = 21.6
What Should You Do with the Remainder?
Question 1.
For each problem below:
- Use numbers, words, or labeled sketches to solve the problem
- Figure out the best way to handle the remainder for that situation
- Write an equation to show each problem and the answer
Story Problem
a. Four friends made 55 cupcakes and shared them equally. How many cupcakes did each friend get?
Your Work:
Answer:
13.75 cupcakes.
Explanation:
Given that:
Four friends made 55 cupcakes and shared them equally.
Number of cupcakes did each friend get,
55 ÷ 4 = 13.75
55 is written as 40 + 15
40 ÷ 4 = 10
15 ÷ 4 = 3 and remainder = 3
Add the quotients 10 + 3 = 13
b. There are 55 kids in the After-School Club. Tomorrow they are going to the zoo. If each car can carry 4 kids, how many cars will they need to get to the zoo?
Your Work:
Answer:
14 cars.
Explanation:
There are 55 kids in the After-School Club.
If each car can carry 4 kids,
Number of cars will they need to get to the zoo,
55 ÷ 4 = 13 and 3 is remainder
4 × 13 = 52
52 + 3 = 55
c. Emma and her 3 friends did chores for Emma’s dad on Saturday. They earned $55.00 and split it evenly. How much money did each of the 4 children get?
Answer:
$13.75
Explanation:
Given that,
Emma and her 3 friends did chores for Emma’s dad on Saturday and earned $55.00.
Total money did each of the 4 children get,
55 ÷ 4 = $13.75
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 4 Session 3 Answer Key
Race Car Problems
Question 1.
Race cars can drive about 5 miles on 1 gallon of gasoline. If a race car goes 265 miles in one race, about how many gallons of gasoline will it use? Show all your work. Note: You can use the base ten area and linear pieces to help solve this problem.
Answer:
53 gallon.
Explanation:
Race cars can drive about 5 miles on 1 gallon of gasoline.
If a race car goes 265 miles in one race,
Total gallons of gasoline will it use, 265 ÷ 5 = 53 gallon.
Question 2.
There were 43 cars in the race. They all finished the 265 miles of the race and they each used about 1 gallon of gas to go 5 miles. About how many gallons of gas did the cars use altogether to finish the race? Show all your work.
Answer:
2,279 gallons.
Explanation:
Given that,
There were 43 cars in the race.
They all finished the 265 miles of the race and they each used about 1 gallon of gas to go 5 miles.
Total gallons of gasoline will it use, 265 ÷ 5 = 53 gallons.
Total gallons of gas did the cars use altogether to finish the race, 53 × 43 = 2,279 gallons.
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 4 Session 4 Answer Key
Quotients Win, Game 2
Red Team ________
Question 1.
140 ÷ 10 = ____
Answer:
14
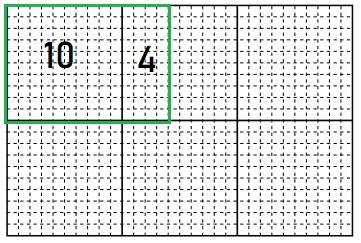
Explanation:
First mark 140 boxes and then divide them into base 10.
we get, 10 + 4 = 14 boxes.
140 ÷ 10 = 14
Question 3.
100 ÷ 20 = ____
Answer:
5
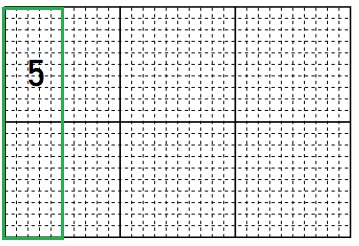
Explanation:
First mark 100 boxes and then divide them into base 20.
we get, 5 boxes.
100 ÷ 20 = 5
Question 5.
100 ÷ 10 = ____
Answer:
10
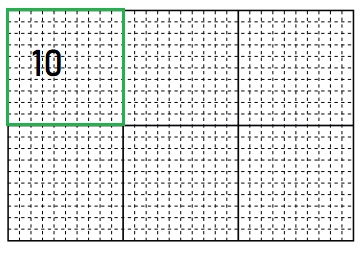
Explanation:
First mark 100 boxes and then divide them into base 10.
we get, 10 boxes.
100 ÷ 10 = 10
Red score _________
Blue Team ________
Question 2.
300 ÷ 20 = ____
Answer:
15
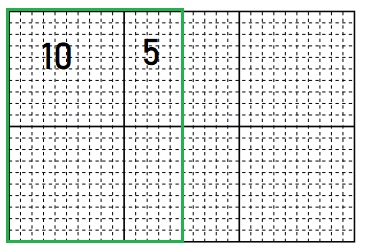
Explanation:
First mark 300 boxes and then divide them into base 20.
we get, 10 + 5 = 15 boxes.
300 ÷ 20 = 15
Question 4.
150 ÷ 15 = ____
Answer:
10
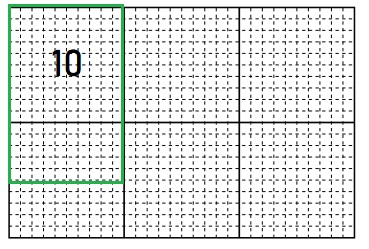
Explanation:
First mark 150 boxes and then divide them into base 15.
we get, 10 boxes.
150 ÷ 15 = 10
Question 6.
260 ÷ 10 = ____
Answer:
26
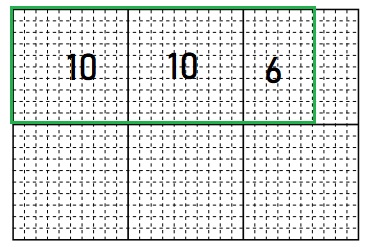
Explanation:
First mark 260 boxes and then divide them into base 10.
we get, 10 + 10 + 6 = 26 boxes.
260 ÷ 10 = 26
Blue score _______
Work Place Instructions 1D Quotients Win
Each pair of players needs:
- 2 copies of one of the 1D Quotients Win Record Sheets (there are 6 different sheets; make sure you each get a copy of the same one)
- 2 dice numbered 1-6
- 1 set of base ten area pieces
- 1 set of base ten linear pieces
- 1 red and 1 blue colored pencil or fine-tip felt marker
Each player gets 1 die and rolls it at the same time. If they both get the same number, they roll again until they have different numbers. Each player solves the problem that has the same number as the number they rolled. Players solve their problems at the same time. Each player makes a labeled sketch of the problem on the record sheet and fills in the answer, using their colored pencil or marker to sketch the dimensions and a regular pencil for the rest of the work. Players can build a model with base ten pieces first, but they don’t have to.
Alisha I rolled a 2, so I have to do problem 2 on the game sheet. That’s 130 ÷ 10. First I’ll lay out a linear strip to show 10 and then start fitting in base ten pieces until I get to 130. My rectangle turned out to be 13 along the other side, so that’s the answer. Now I have to make a sketch.
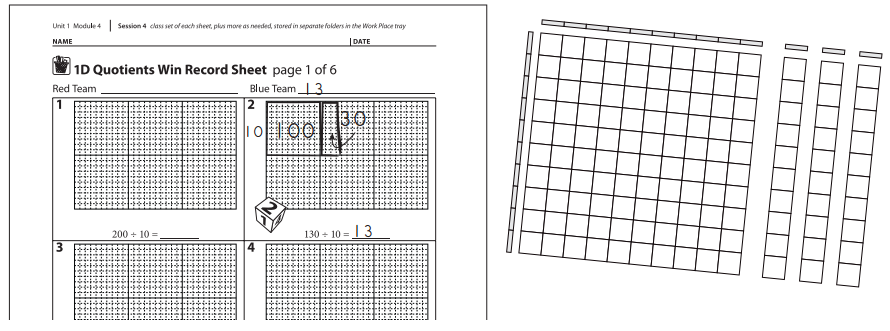Players roll and solve the problems until they have each solved 3. If they roll the number of a problem that has already been solved, they roll again until they get the number of a problem that has not been solved yet. (Players must use the first number that has not been solved). When they are done, they check each other’s work. At the end of the game, players add their quotients and record their score at the bottom of the sheet. The player with the higher score wins.
Game Variations
A. Players take turns instead of both going at once. They sketch and solve their partner’s problems as well as their own on their record sheet. They work together to make sure their answers are correct.
B. Players use Record Sheets 5 and 6, which are much more challenging.
Multiplication & Division Problems
Question 1.
Fill in the missing numbers.
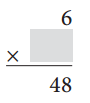
Answer:
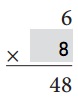
Explanation:
We know that multiplication is the inverse operation of division.
6 × 8 = 48
48 ÷ 6 = 8
Answer:
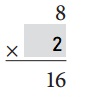
Explanation:
We know that multiplication is the inverse operation of division.
8 × 2 = 16
16 ÷ 8 = 2
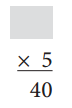
Answer:
Explanation:
We know that multiplication is the inverse operation of division.
8 × 5 = 40
40 ÷ 8 = 5
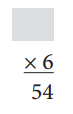
Answer:
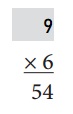
Explanation:
We know that multiplication is the inverse operation of division.
9 × 6 = 54
54 ÷ 9 = 6
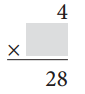
Answer:
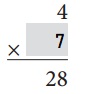
Explanation:
We know that multiplication is the inverse operation of division.
4 × 7 = 28
28 ÷ 4 = 7
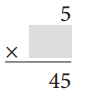
Answer:
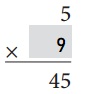
Explanation:
We know that multiplication is the inverse operation of division.
5 × 9 = 45
45 ÷ 5 = 9
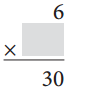
Answer:
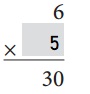
Explanation:
We know that multiplication is the inverse operation of division.
6 × 5 = 30
30 ÷ 6 = 5
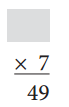
Answer:
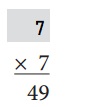
Explanation:
We know that multiplication is the inverse operation of division.
7 × 7 = 49
49 ÷ 7 = 7
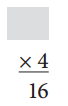
Answer:
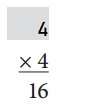
Explanation:
We know that multiplication is the inverse operation of division.
4 × 4 = 16
16 ÷ 4 = 4
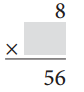
Answer:
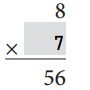
Explanation:
We know that multiplication is the inverse operation of division.
8 × 7 = 56
56 ÷ 8 = 7
Question 2.
Write an equation to answer each question below.
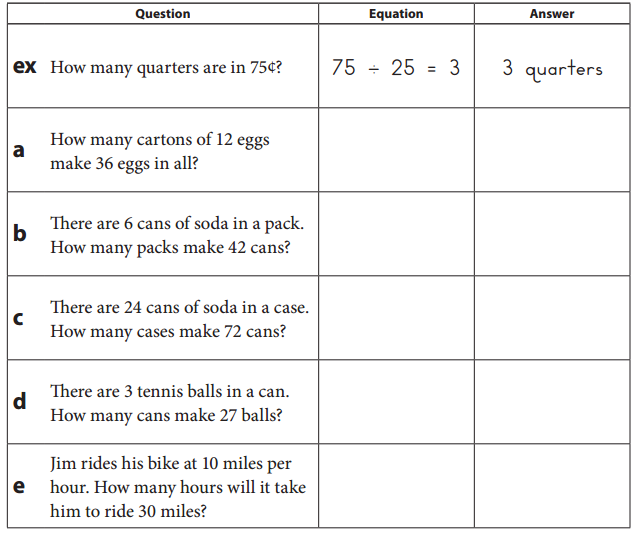
Answer:
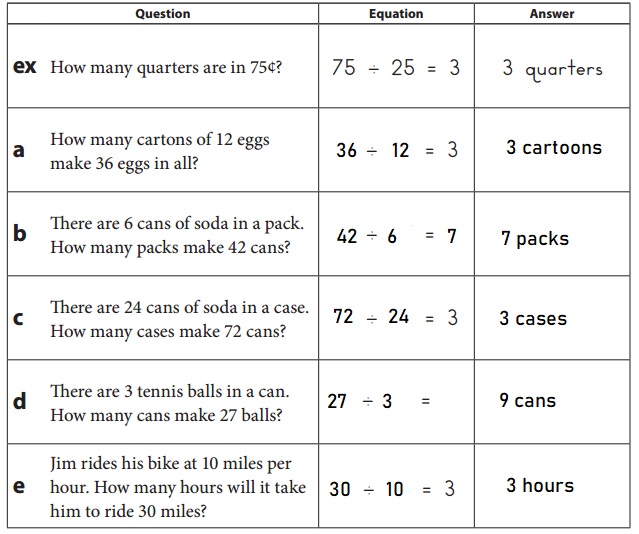
Explanation:
We know that multiplication is the inverse operation of division as shown in the above table.
Bridges in Mathematics Grade 5 Student Book Unit 1 Module 4 Session 5 Answer Key
Using Basic Facts to Solve Larger Problems
Knowing the basic multiplication and division facts can help you multiply larger numbers too. Start with the basic facts below and then complete the related fact family of larger numbers. Then make up your own fact family based on other related numbers.
Basic Fact Family
ex
4 × 3 = 12
3 × 4 = 12
12 ÷ 4 = 3
12 ÷ 3 = 4
Related Fact Family
40 × 3 = 120
3 × 40 = 120
120 ÷ 40 = 3
120 ÷ 3 = 40
Your Own Related Fact Family
40 × 30 = 1,200
30 × 40 = 1,200
1,200 ÷ 40 = 30
1,200 ÷ 30 = 40
Question 1.
Basic Fact Family
_____ × _____ = _____
6 × 8 = 48
_____ ÷ ____ = _____
48 ÷ 6 = 8
Answer:
8 × 6 = 48
6 × 8 = 48
48 ÷ 8 = 6
48 ÷ 6 = 8
Related Fact Family
80 × 6 = 480
____ × ____ = ____
480 ÷ 80 = 6
____ ÷ ____ = ____
Answer:
80 × 6 = 480
6 × 80 = 480
480 ÷ 80 = 6
480 ÷ 6 = 80
Your Own Related Fact Family
____ × ____ = ____
____ × ____ = ____
____ ÷ ____ = ____
____ ÷ ____ = ____
Answer:
80 × 60 = 4,800
60 × 80 = 4,800
4,800 ÷ 60 = 80
4,800 ÷ 80 = 60
Explanation:
A fact family can be defined as a collection of math facts that express the relation between the same set of numbers like multiplication and division as shown above.
Question 2.
Basic Fact Family
_____ × _____ = _____
9 × 4 = 36
_____ ÷ ____ = _____
36 ÷ 9 = 4
Answer:
4 × 9 = 36
9 × 4 = 36
36 ÷ 4 = 9
36 ÷ 9 = 4
Related Fact Family
40 × 9 = 360
____ × ____ = ____
360 ÷ 40 = 9
____ ÷ ____ = ____
Answer:
40 × 9 = 360
9 × 40 = 360
360 ÷ 40 = 9
360 ÷ 9 = 40
Your Own Related Fact Family
____ × ____ = ____
____ × ____ = ____
____ ÷ ____ = ____
____ ÷ ____ = ____
Answer:
400 × 90 = 36,000
90 × 400 = 36,000
36000 ÷ 90 = 400
36000 ÷ 400 = 90
Explanation:
A fact family can be defined as a collection of math facts that express the relation between the same set of numbers like multiplication and division as shown above.
Question 3.
Basic Fact Family
_____ × _____ = _____
7 × 3 = 21
_____ ÷ ____ = _____
21 ÷ 7 = 3
Answer:
3 × 7 = 21
7 × 3 = 21
21 ÷ 3 = 7
21 ÷ 7 = 3
Related Fact Family
30 × 7 = 210
____ × ____ = ____
210 ÷ 30 = 7
____ ÷ ____ = ____
Answer:
30 × 7 = 210
7 × 30 = 210
210 ÷ 30 = 7
210 ÷ 7 = 30
Your Own Related Fact Family
____ × ____ = ____
____ × ____ = ____
____ ÷ ____ = ____
____ ÷ ____ = ____
Answer:
300 × 70 = 21000
70 × 300 = 21000
21000 ÷ 70 = 300
21000 ÷ 300 = 70
Explanation:
A fact family can be defined as a collection of math facts that express the relation between the same set of numbers like multiplication and division as shown above.