Students looking for the Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 5 Module 2 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 5 Module 2
Bridges in Mathematics Grade 5 Home Connections Unit 5 Module 2 Session 2 Answer Key
The Tangerine Problem
Question 1.
Estimate the results of 360 ÷ 24 and explain your thinking.
Answer:
15,
Explanation:
Let’s estimate the results of 360 ÷ 24 we get
24)360(15
24
120
120
0
Question 2.
Fill in the ratio table for 24, and use it to help solve 360 ÷ 24. You can make a sketch, or you can work with numbers only.

Answer:

Explanation:
Asked to fill in the ratio table for 24 and use it to help solve 360 ÷ 24 made a sketch to work with numbers only we the results as 15 or 24 X 15 = 360.
Question 3.
Ali says that if you divide 360 by 12 instead of 24, the answer will be twice as large. Do you agree with her or not? Why?
Answer:
Yes, I agree,
Explanation:
Ali says if we divide 360 by 12 instead of 24 the answer will be twice as large so lets check 360 ÷ 12 we get 30 and 360 ÷ 24 = 15, I agree 30 is twice large as 15.
Question 4.
Holly and her brother Max got permission to pick tangerines from the trees in their yard and sell them to their friends and neighbors. In all, they collected 360 tangerines.
Holly thinks they should put the tangerines in bags of 24 and sell each bag for $1.50.
Max thinks they should divide the tangerines equally among 24 bags and sell each bag for $1.50.
Whose plan is better? Why? Show all of your your work below.
Answer:
Both plans are better only, But the best plan is Max which is equal distribution among the bags,
Explanation:
We have Holly and her brother Max got permission to pick tangerines from the trees in their yard and sell them to their friends and neighbors. In all, they collected 360 tangerines.
Holly thinks they should put the tangerines in bags of 24 and sell each bag for $1.50.
Max thinks they should divide the tangerines equally among 24 bags and sell each bag for $1.50.
Better is the plan of Max as he has distributed it equally among 24 bags we get 360 ÷ 24 = 15 bags of tangerines,
Now Holly put his tangerines in the bags as factors of 24, 24 = 1, 2, 3, 4, 6, 8,12, 24, 360 ÷ 24 = 15, therefore both plans are better only, But the best plan is Max which is equal distribution among the bags.
Bridges in Mathematics Grade 5 Home Connections Unit 5 Module 2 Session 4 Answer Key
Fractions & Division
Question 1.
Complete the box challenges.
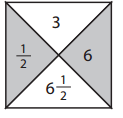
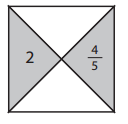
ex:
a.
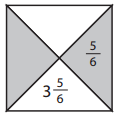
Answer:
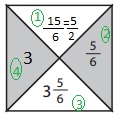
Explanation:
In given example 2nd part is 6 and part 1 is multiple of part 2 of part 4 we get 6 X \(\frac{1}{2}\) = 3 and
part 3 is addition of part 2 and part 4 we get 6 + \(\frac{1}{2}\) = \(\frac{13}{2}\) or 6\(\frac{1}{2}\).
Now in the given figure part 3 is \(\frac{5}{6}\) so part 4 is subtraction of part 3 of and part 2 we get 3\(\frac{5}{6}\) – \(\frac{5}{6}\) = \(\frac{3 X 6 + 5}{6}\) – \(\frac{5}{6}\) = \(\frac{23}{6}\) – \(\frac{5}{6}\) = \(\frac{23 – 5}{6}\) = \(\frac{18}{6}\) = 3.
Now part 1 is multiple of part 2 of part 4 we get \(\frac{5}{6}\) X 3 = \(\frac{5 X 3}{6}\) = \(\frac{15}{6}\) both goes by 3 we get \(\frac{5 X 3}{3 X 2}\) = \(\frac{5}{2}\).
b.
Answer:
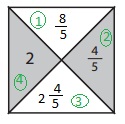
Explanation:
In given figure part 2 is \(\frac{4}{5}\) and part 4 is 2 so part 3 is 2 + \(\frac{4}{5}\) = \(\frac{2 X 5 + 4}{5}\) = \(\frac{14}{5}\) as numerator is greater than denominator we write in mixed fraction as 2\(\frac{4}{5}\),
Question 2.
Find the product of each.
a. 11 × \(\frac{1}{2}\) = ________________
Answer:
\(\frac{11}{2}\),
Explanation:
Given to find the product of 11 X \(\frac{1}{2}\) so we get \(\frac{11 X 1}{2}\) = \(\frac{11}{2}\).
b. \(\frac{3}{8}\) × 16 = _______________
Answer:
6,
Explanation:
Given to find the product of \(\frac{3}{2}\) X 16 so we get \(\frac{3 X 16}{8}\) = \(\frac{3 X 2}{1}\) = 6.
c. \(\frac{7}{3}\) × 12 = _______________
Answer:
28,
Explanation:
Given to find the product of \(\frac{7}{3}\) X 12 so we get \(\frac{7 X 12}{3}\) = \(\frac{7 X 4}{1}\) = 28.
d. 15 × \(\frac{2}{3}\) = _______________
Answer:
10,
Explanation:
Given to find the product of 15 X \(\frac{2}{3}\) so we get \(\frac{15 X 2}{3}\) = \(\frac{5 X 2}{1}\) = 10.
Question 3.
Fill in the blank.
a. 19 × \(\frac{5}{5}\) = _______________
Answer:
19,
Explanation:
Given to find the product of 19 X \(\frac{5}{5}\), so we get \(\frac{19 X 5}{5}\) = 19.
b. \(\frac{12}{12}\) × ______________ = 14
Answer:
14,
Explanation:
Let the missing number be n so we get \(\frac{12}{12}\) X n =14 therefore n = \(\frac{12}{12}\) X 14 = 14.
Question 4.
Fill in the ratio table for 23.

Answer:

Explanation:
Asked to fill in the ratio table for 23 and use it to help solve the table as number of groups as 1,2,10,5,20,15,30,20,40 an total as multiple of 23 each by number of groups we get 23,46,230,115,460,345,690,460,920.
Question 5.
Solve these two division problems using the ratio table above. You can add to the ratio table if you want to.
ex: 368 ÷ 23 = 16
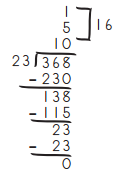
a. 529 ÷ 23 = _______________
Answer:
23,
Explanation:
23)529(23
-46
69
-69
0
b. 414 ÷ 23 = ________________
Answer:
18,
Explanation:
23)414(18
23
184
184
0
Question 6.
Jill grew out her hair for several years to donate to charity. When she was finally ready to have it cut, she asked her mother to take off 10\(\frac{2}{3}\) inches. She liked it short so much that she got another 1\(\frac{7}{8}\) inches cut off.
a. How much hair did Jill have cut off in all? Show your work.
Answer:
\(\frac{325}{24}\) inches or 15\(\frac{13}{24}\) inches,
Explanation:
We have Jill grew out her hair for several years to donate to charity. When she was finally ready to have it cut, she asked her mother to take off 10\(\frac{2}{3}\) inches. She liked it short so much that she got another 1\(\frac{7}{8}\) inches cut off.
Hair did Jill have cut off in all 10\(\frac{2}{3}\) inches + 1\(\frac{7}{8}\) inches = \(\frac{10 X 3 + 2}{3}\) inches + \(\frac{1 X 8 + 7}{8}\) inches = \(\frac{35}{3}\) inches + \(\frac{15}{8}\) inches = \(\frac{35 X 8 + 15 X 3}{24}\) inches = \(\frac{280}{24}\) + \(\frac{45}{24}\) = \(\frac{325}{24}\) inches as numerator is greater than denominator we get \(\frac{15 X 24 + 13}{24}\) inches = 15\(\frac{13}{24}\) inches.
b. How much more hair was cut off the first time than the second? Show your work.
Answer:
\(\frac{235}{24}\),
Explanation:
More hair was cut off the first time than the second time is \(\frac{35}{3}\) inches – \(\frac{15}{8}\) inches = \(\frac{35 X 8 – 15 X 3}{24}\) inches = \(\frac{280}{24}\) – \(\frac{45}{24}\) = \(\frac{280 – 45}{24}\) = \(\frac{235}{24}\).
c. Jill estimates that her hair will grow \(\frac{2}{3}\) of an inch every month. How much longer will her hair be in 10 months than it is now? Show your work.
Answer:
\(\frac{20}{3}\),
Explanation:
As Jill estimates that her hair will grow \(\frac{2}{3}\) of an inch every month. Much longer will her hair be in 10 months than it is now \(\frac{2}{3}\) X 10 = \(\frac{2 X 10}{3}\) = \(\frac{20}{3}\) as numerator is greater than denominator we get \(\frac{3 X 6 + 2}{3}\) inches = 6\(\frac{2}{3}\) inches.
Question 7.
CHALLENGE. Cameron loves to read and has a big collection of books. Half of them are fantasy, one-fourth of them are biographies, one-eighth of them are mysteries, and 6 of them are sports books. How many books does Cameron have in all? How many of them are fantasy, how many of them are biographies, and how many of them are mysteries? Show your work.

Answer:
\(\frac{55}{8}\) = 6\(\frac{7}{8}\) books,
Fantasy Books : \(\frac{55}{4}\) or 13\(\frac{3}{4}\),
Biographies Books : \(\frac{55}{2}\) or 27\(\frac{1}{2}\),
Mysteries Books: 55,
Explanation:
As Cameron loves to read and has a big collection of books. Half of them are fantasy, one-fourth of them are biographies, one-eighth of them are mysteries, and 6 of them are sports books. Number of books does Cameron have in all are \(\frac{1}{2}\) + \(\frac{1}{4}\) + \(\frac{1}{8}\) + 6 will have common denominator as 8 we get \(\frac{1 X 4}{8}\) + \(\frac{1 X 2}{8}\) + \(\frac{1 X 1}{8}\) + \(\frac{6 X 8}{8}\) = \(\frac{4 + 2 + 1 + 48}{8}\) = \(\frac{55}{8}\) as numerator is greater than denominator we get \(\frac{8 X 6 + 7}{8}\) = 6\(\frac{7}{8}\) books. As number of books of fantasy are half so they are \(\frac{55}{8}\) X \(\frac{2}{1}\) = \(\frac{55}{4}\) = \(\frac{13 X 1 + 3}{4}\) or 13\(\frac{3}{4}\), Number of books biographies are \(\frac{55}{8}\) X \(\frac{4}{1}\) = \(\frac{55 X 1}{2}\) = \(\frac{55}{2}\) or 27\(\frac{1}{2}\), Number of Mysteries Books are \(\frac{55}{8}\) X \(\frac{8}{1}\) = \(\frac{55}{1}\) = 55.