Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 6 Module 4 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 6 Module 4
Bridges in Mathematics Grade 4 Student Book Unit 6 Module 4 Session 1 Answer Key
Work Place Instructions 6D Lowest Remainder Wins
Each pair of players needs:
- 2 copies of the 6D Lowest Remainder Wins Record Sheets
- 1 die numbered 0-5
- 2 dice numbered 1-6
- 1 spinner overlay
1. Players decide who will go first. One player spins the spinner to get the first divisor for both players.
2. Players start a ratio table for the divisor in the Round 1 box on their record sheets. They fill in the ratio table for 10, 20, and 5.
3. Each player rolls either two dice (for a 2-digit dividend) or three dice (for a 3-digit dividend). Players may arrange the digits in any order to make a dividend.
Players should try to make a number that won’t leave a remainder when it is divided by the divisor. If that doesn’t work, they try to make a number that will leave a very small remainder.
4. Each player records her division problem on her own record sheet and solves it.
Players add any useful combinations to their ratio table to help.
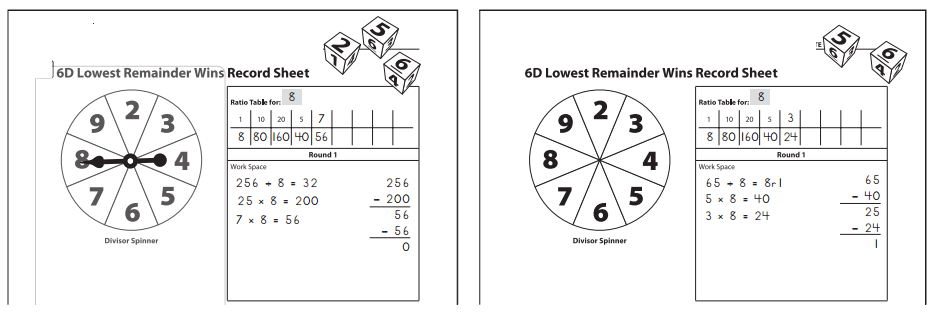
5. When both players have solved their division problems, they explain their work to each other. When both players agree that each other’s work is correct, they enter their scores on the scorecard at the bottom of their record sheets.
Players get 0 points if they have no remainder. Otherwise, players get the number of points that matches their remainder. (For example, a remainder of 3 scores 3 points.)
6. After completing three rounds, players add the points to get their total scores. The player with the lower score wins.
Game Variations
A. Players can use the challenge record sheets instead of the regular record sheets for this game. The challenge sheets have a spinner with higher divisors.
B. Players can use two dice marked 4-9 and one die marked 1-6.
C. Players can use four dice to try dividing some 4-digit numbers.
Answer:
David Goes Shopping
Solve each problem below. Choose the strategy that is easiest for you. Show your work.
Question 1.
David gave $272 worth of books to the local library. Each book was worth $8. How many books did he give to the library?
David gave _____________ books to the library.
Answer:
David gave 34 books to the library.
Explanation:
Given,
David gave $272 worth of books to the local library.
Each book was worth $8.
We need to find how many books did he give to the library?
272 ÷ 8 = 34
Hence David gave 34 books to the library.
Question 2.
David spend $216 on plants for his business. He bought 9 plants. If each plant cost the same amount, how much did one plant cost?
One plant cost ____________.
Answer:
One plant cost $24.
Explanation:
Given,
David spent $216 on plants.
David bought 9 plants.
To find: how much did one plant cost?
216 ÷ 9 = $24
Hence one plant cost $24.
Question 3.
David spent $408 on DVDs over the past few years. Each DVD cost $17. How many DVDs did he buy? (You do not have to use the ratio table, but it might help you solve the problem.)

David bought ________________ DVDs.
Answer:
David bought 24 DVDs.
Explanation:
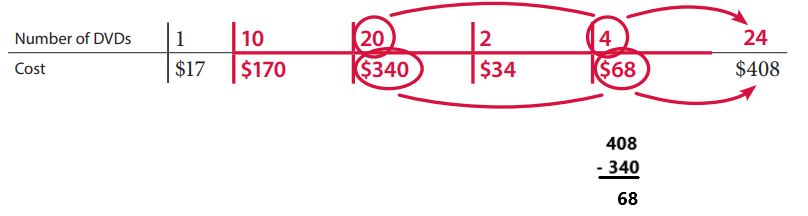
Bridges in Mathematics Grade 4 Student Book Unit 6 Module 4 Session 2 Answer Key
School Carnival
Brightwood School is holding a carnival to earn money for new library books.
Question 1.
Jarrod and his 7 friends sold tickets at the front gate. They were supposed to keep track of how many tickets each person sold, but they forgot. They sold a total of 792 tickets. If each of the 8 children sold the same number of tickets, how many tickets did Jarrod sell?
Answer:
Jarrod sold 99 tickets.
Explanation:
Total no of tickets = 792
No of children = 8
792 ÷ 8 = 99
Hence Jarrod sold 99 tickets.
Question 2.
During the carnival Madison and 8 of her friends collected tickets at the Jumpy Castle. They collected a total of 135 tickets. If each of the 9 children collected the same number of tickets, how many tickets did Madison collect?
Answer:
The number of tickets Madison collected are 15.
Explanation:
Given,
Total no of tickets are 135.
No of children = 9
135 ÷ 9 = 15
Hence the number of tickets Madison collected are 15.
Question 3.
594 ÷ 6
Answer:
The division to the given number is 99.
Explanation:
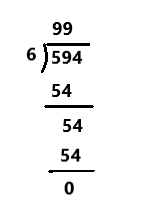
Question 4.
120 ÷ 8
Answer:
The division to the given number is 15.
Explanation:
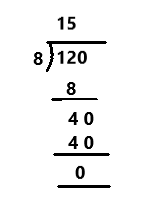
Remainder Review
Question 1.
Julia spilled ketchup on her paper and can’t see a part of the problem anymore.

a. How many beads did Martha have? Fill in the blank: ____________ ÷ 7 = 3 r 2.
Answer:
23 ÷ 7 = 3 r 2.
b. What does the remainder of 2 mean in this problem?
Answer:
She had 2 beads left over.
Question 2.
Each of the division problems below includes a remainder. Solve each and show your work. Figure out the best way to treat the remainder for each one: as a whole number, a fraction, or a decimal.
a. Rachel earned $46 dollars for walking dogs Monday through Friday last week. If she earned the same amount every day, how much did she earn per day?
Answer:
She earned $9.20 per day.
Explanation:
She made a total of $46 from Monday through Friday.
That is a total of five days.
So 46 ÷ 5 = $9.20 per day.
b. Bryson bought 27 balloons to share with three friends. How many balloons does each of the 4 children get?
Answer:
There are 6 balloons with 3 balloons left over.
Explanation:
Given,
Bryson bought 27 balloons.
No of children = 4
27 ÷ 4 = 6 R3
Hence there are 6 balloons with 3 balloons left over.
c. Ropes come in 16 foot lengths at the hardware store. Jorge bought one rope and then cut it into three equal size pieces. How long was each of the three pieces?
Answer:
5 \(\frac{1}{3}\) feet.
Explanation:
Given,
Ropes come in 16 foot lengths at the hardware store.
One rope cut it into three equal size pieces.
16 ÷ 3
5 \(\frac{1}{3}\) feet.
Question 3.
Abby did a story problem and got 30 ÷ 4 = 7 R2 as the answer. Write a problem that could have been the one Abby solved.
Answer:
The problem we could write is
There are 81 toffees. 9 toffees are to be packed in each box. How many boxes do we need?
Bridges in Mathematics Grade 4 Student Book Unit 6 Module 4 Session 3 Answer Key
Tessa’s Tickets
Tessa is performing in a production of The Wizard of Oz. She began selling tickets two weeks before the show’s opening night. Show your work on each of the problems below.
Question 1.
Adult tickets cost $7.00.
a. How much do 28 adult tickets cost?
Answer:
$196
Explanation:
Given,
Cost of adult tickets is $7.
We need to find How much do 28 adult tickets cost?
28 × 7 = $196.
b. Tessa’s neighbor spent $105 on adult tickets. How many tickets did her neighbor buy?
Answer:
No of tickets neighbor bought is 15.
Explanation:
Given,
Adult tickets cost $7.00.
Tessa’s spent on adult tickets = $105
105 ÷ 7 = 15
Hence no of tickets neighbor bought is 15.
Question 2.
Children’s tickets cost $4.00.
a. How much do 136 children’s tickets cost?
Answer:
$544.
Explanation:
Given,
Cost of Children’s tickets = $4
We need to find cost of 136 children’s tickets.
136 × $4 = $544
b. Tessa’s aunt spent $96 on children’s tickets. How many tickets did her aunt buy?
Answer:
Her aunt bought 24 tickets.
Explanation:
Given,
Cost of Children’s tickets = $4
Tessa’s aunt spent $96 on children’s tickets.
We need to find how many tickets did her aunt buy?
$96 ÷ 4 = $24
Hence her aunt bought 24 tickets.
Question 3.
CHALLENGE Tessa’s teacher spent $44 on tickets. He bought some tickets for children and some for adults. How many children’s tickets and how many adult tickets did Tessa’s teacher buy?
Answer:
4 children’s tickets and 4 adult tickets.
Explanation:
Given,
Tessa’s teacher spent $44 on tickets.
We need to find how many children’s tickets and how many adult tickets did Tessa’s teacher buy.
Therefore he bought 4 children’s tickets and 4 adult tickets.