Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 6 Module 2 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 6 Module 2
Bridges in Mathematics Grade 4 Student Book Unit 6 Module 2 Session 1 Answer Key
Area Challenges
Question 1.
A certain rectangle has an area of 693 square meters. This rectangle is 7 meters wide. How long is it?
a. Make a sketch that shows what you know about the situation.
Answer:
The length of the rectangle will be 99m.
Explanation:
The area of rectangle is 693 sq meters and the wide of the rectangle is 7 meters. So the length of the rectangle will be
Area = LW
693 = 7×L
L = 693÷7
= 99 m.
b. Write an equation to represent the problem.
Answer:
693÷7 = 99 m.
Explanation:
The equation to represent the problem is 693÷7 = 99 m.
c. Use an array or a ratio table to model and solve the problem. Show all of your work.
Answer:
The array model to solve this problem is
= (100×7)-(1×7)
= 700 – 7
= 693
Question 2.
Use an array or a ratio table to model and solve problems 2a and 2b. Show all of your work.
a. A paved bike trail has an area of 7,147 square feet. If the trail is 7 feet wide, how long is the trail?
Answer:
The length of the trail is 1,021.
Explanation:
Here, we know the area which is 7,147 square feet and width is 7 feet. So the length of the trail will be
7,147 ÷ 7 = 1,021.
b. 3,521 ÷ 7 = ______________
Answer:
3,521 ÷ 7 = 503.
Explanation:
The division of the given numbers is equal to 503.
Question 3.
CHALLENGE Use a ratio table or an array to model and solve each of the problems below. Show all of your work. If you think you’ll need more room, do these problems in your math journal.
a. 340 ÷ 8 = ______________
Answer:
The answer for the given division is 42.5
Explanation:
The given question is 340 ÷ 8
When you divide 340 by 8, the quotient is 42.5.
b. Petra is raking leaves in her backyard. Petra’s backyard is rectangular and has an area of 476 square feet. One side of the backyard is 28 feet. How long is the other side?
Answer:
The width of Petra’s backyard is 17 feet.
Explanation:
The area of the rectangle is length × width
We know that the area of Petra’s backyard is 476 square feet.
And we know that one side of the backyard is 28 feet.
Let’s use the variable w to represent the width of the backyard.
Then the area of the backyard is
476 = 28w
w = 476 ÷ 28
w = 17
the width of Petra’s backyard is 17 feet.
c. 900 ÷ 36 = _____________
Answer:
The answer is 25.
Explanation:
The division of the given number is equal to 25.
Quinn’s Quilt
Question 1.
Read each problem below. First make an estimate. Then write an equation with a letter standing for the unknown quantity. Finally, solve the problem. Show your work using numbers, labeled sketches, or words.
a. Quinn made a quilt. The quilt is 72 inches by 96 inches. What is the area of Quinn’s quilt?
Estimate: _______________
Equation: _______________
Answer:
The estimate answer is 6900 square inches.
The equation is Area = 69 × 72
Explanation:
Given,
The length of the quilt is 96 inches
Width of the quilt is 72 inches.
Area of the Quinn’s quilt is 96 × 72
= 6912 square inches.
b. Quinn made a pillowcase to go with her quilt. The area of the top of the pillowcase is 189 in2 (square inches). One dimension of the pillowcase is 9 inches. What is the other dimension?
Estimate: ________________
Equation: ________________
Answer:
The estimate is 20 inches.
The equation is 189 ÷ 9
Explanation:
The area of the rectangle is length × width
Area of the top of the pillowcase is 189 in2 (square inches).
One dimension of the pillowcase is 9 inches.
The equation based on the formula for the area is
189 = 9w
189 ÷ 9 = 21
w = 21 inches.
The other dimension of the pillow case is 21 inches.
Question 2.
Solve the following problems. Show your work.
25 × 38 = _______________
600 ÷ 8 = ________________
Answer:
950 and 75.
Explanation:
The multiplication of the given numbers is 950.
The division for the given numbers is 75.
Bridges in Mathematics Grade 4 Student Book Unit 6 Module 2 Session 2 Answer Key
String Rectangles
Use your 60-inch length of string, some small bits of masking tape, a measuring tape, and numbers to help solve the problems below. Use equations and labeled sketches to show your work.
Question 1.
If you use your string to form a rectangle with one dimension of 24 inches, what is the length of the other dimension? Make a labeled sketch of the rectangle, and use one or more equations to find or check your answer.
The length of the other dimension is ______________ inches.
Answer:
The length of the other dimension is 6 inches.
Explanation:
Given,
The perimeter of the rectangle is equal to the length of the string which is 60 inches.
Perimeter = 2 (length + width)
60 = 2 × (24 + x)
60 = 48 + 2x
2x = 60 – 48
2x = 12
x = 12 ÷ 2
x = 6
Therefore the length of the other dimension is 6 inches.
Question 2.
If you use your string to form a rectangle with one dimension of 19 inches, what is the length of the other dimension? Make a labeled sketch of the rectangle, and use one or more equations to find and/or check your answer.
The length of the other dimension is ______________ inches.
Answer:
The length of the other dimension is 11 inches.
Explanation:
The perimeter of the rectangle (the sum of all sides) is equal to the length of the string, which is 60 inches.
perimeter = 2 × (l + w)
60 = 2 × (19 + x)
60 = 38 + 2x
2x = 60 – 38
2x = 22
x = 22 ÷ 2
x = 11
The length of the other dimension is 11 inches.
Question 3.
Jason says it’s possible to form a square with a 60″ length of string. Use a labeled sketch and one or more equations to prove that Jason is correct.
Answer:
By using the 60-inch length of string, we can form a square with each side measuring 15 inches. This proves that Jason is correct.
Explanation:
Given,
Each side of the square is s inches.
perimeter of the square is
p = 4 × s
According to the problem the perimeter of a square is equal to the length of the string which is 60 inches.
Therefore the equation is
4s = 60
s = 60 ÷ 4
s = 15
the each side of the square is 15 inches.
Question 4.
CHALLENGE How many different rectangles with dimensions that are whole numbers can you make with a 60″ piece of string? List them in your journal, and record the answer here.
You can make ______________ different rectangles with a 60″ piece of string.
Answer:
There are 15 different rectangles with dimensions that are whole numbers that can be made with a 60″ piece of string.
Explanation:
Let’s go through each possible combination and calculate the perimeter to check if it equals 60″.
let us assume
1. Length = 1″, Width = 29″
Perimeter = 2 × (Length + Width) = 2 × (1 + 29) = 2 × 30 = 60
2. Length = 2″, Width = 28″
Perimeter = 2 × (Length + Width) = 2 × (2 + 28) = 2 × 30 = 60
3. Length = 3″, Width = 27″
Perimeter = 2 × (Length + Width) = 2 × (3 + 27) = 2 × 30 = 60
4. Length = 4″, Width = 26″
Perimeter = 2 × (Length + Width) = 2 × (4 + 26) = 2 × 30 = 60
5. Length = 5″, Width = 25″
Perimeter = 2 × (Length + Width) = 2 × (5 + 25) = 2 × 30 = 60
6. Length = 6″, Width = 24″
Perimeter = 2 × (Length + Width) = 2 × (6 + 24) = 2 × 30 = 60
7. Length = 7″, Width = 23″
Perimeter = 2 × (Length + Width) = 2 × (7 + 23) = 2 * 30 = 60
8. Length = 8″, Width = 22″
Perimeter = 2 × (Length + Width) = 2 × (8 + 22) = 2 × 30 = 60
9. Length = 9″, Width = 21″
Perimeter = 2 × (Length + Width) = 2 × (9 + 21) = 2 × 30 = 60
10. Length = 10″, Width = 20″
Perimeter = 2 × (Length + Width) = 2 × (10 + 20) = 2 × 30 = 60
11. Length = 11″, Width = 19″
Perimeter = 2 × (Length + Width) = 2 * (11 + 19) = 2 * 30 = 60
12. Length = 12″, Width = 18″
Perimeter = 2 × (Length + Width) = 2 × (12 + 18) = 2 × 30 = 60
13. Length = 13″, Width = 17″
Perimeter = 2 × (Length + Width) = 2 × (13 + 17) = 2 × 30 = 60
14. Length = 14″, Width = 16″
Perimeter = 2 × (Length + Width) = 2 × (14 + 16) = 2 × 30 = 60
15. Length = 15″, Width = 15″
Perimeter = 2 × (Length + Width) = 2 × (15 + 15) = 2 × 30 = 60
Therefore there are 15 different rectangles with dimensions that are whole numbers that can be made with a 60″ piece of string.
Kaylee’s Kilometers
Kaylee is training to run a marathon next summer. Help Kaylee figure out how far she is running each day. Show your work with numbers, labeled sketches, or words.
Question 1.
There is a rectangular path for running in Kaylee’s town. She runs around the path every day. One side of the path is 5\(\frac{1}{2}\) kilometers long. Another side is 3\(\frac{1}{2}\) kilometers long.
a. What is the perimeter of the path?
Answer:
The perimeter of the path is 18 km.
Explanation:
Given,
Length of one side is 5\(\frac{1}{2}\) = \(\frac{11}{2}\)
Length of the other side is 3\(\frac{1}{2}\) = \(\frac{7}{2}\)
Lets add the length of all sides
perimeter = length of side 1 + length of side 2 + length of side 3 + length of side 4
perimeter = 5.5 + 3.5 + 5.5 + 3.5
= 18 km
The perimeter of the path is 18 km.
b. If Kaylee ran around the path 7 times during one week, how many kilometers did she run that week?
Answer:
Kaylee ran a total of 126 kilometers in one week by running around the path 7 times.
Explanation:
Given,
the distance covered in one lap is 18 km.
We need calculate the total distance covered in one week:
Total distance = Distance × Number of laps
Total distance = 18 kilometers × 7
= 126 kilometers
c. How many meters did Kaylee run that week?
Answer:
Kaylee runs a total of 63,000 meters in a week on the rectangular path.
Explanation:
Let’s convert the lengths of the sides of the path from kilometers to meters:
One side of the path: 5\(\frac{1}{2}\) = 5500 meters
Another side of the path: 3\(\frac{1}{2}\) = 3500 meters
let’s calculate the total distance Kaylee runs in one day by adding the lengths of both sides:
Total distance in one day = 5500 meters + 3500 meters = 9000 meters
To find the total distance Kaylee runs in a week, we multiply the distance in one day by seven:
Total distance in a week = 9000 meters × 7 = 63,000 meters
Therefore, Kaylee runs a total of 63,000 meters in a week on the rectangular path.
d. It takes Kaylee 1\(\frac{5}{6}\) hours to run around the path. How many minutes does it take Kaylee to run around the path?
Answer:
It takes Kaylee 110 minutes to run around the path.
Explanation:
Let us convert the time given in hours and minutes to minutes only.
First, let’s convert 1 hour and \(\frac{5}{6}\) hours to minutes.
1 hour = 60 minutes
\(\frac{5}{6}\) × 60 = 50 minutes
So, 1 hour and 5/6 hours is equal to 60 + 50 = 110 minutes.
e. CHALLENGE Kaylee ran around the path 1\(\frac{1}{2}\) times three days in a row. How far did she run on those three days in all?
Answer:
Kaylee ran a total distance of 40.5 kilometers on those three days.
Explanation:
We need to calculate the distance she covered for each lap and then multiply it by the number of laps.
The length of one side of the path is 5\(\frac{1}{2}\) kilometers.
The length of the other side of the path is 3\(\frac{1}{2}\) kilometers.
To calculate the distance covered in one lap, we add the lengths of both sides:
Distance per lap = 5\(\frac{1}{2}\) + 3\(\frac{1}{2}\)
\(\frac{11}{2}\) + \(\frac{7}{2}\)
\(\frac{(11+7)}{2}\)
\(\frac{(18)}{2}\)
9 km.
Since Kaylee ran around the path 1\(\frac{1}{2}\) times for each of the three days, we can calculate the total distance covered by multiplying the distance per lap by the number of laps:
Total distance = Distance per lap × Number of laps
Total distance = 9 kilometers × (1\(\frac{1}{2}\) laps × 3 days)
To multiply a whole number by a mixed number, we can convert the mixed number into an improper fraction:
Total distance = 9 kilometers × (\(\frac{3}{2}\) × 3)
Next, we simplify the expression:
Total distance = 9 kilometers × (\(\frac{3}{2}\))
To multiply fractions, we multiply the numerators together and the denominators together:
Total distance = (9 × 9) kilometers ÷ (2 × 1)
Total distance = 81 kilometers ÷ 2
Finally, we divide the numerator by the denominator:
Total distance = 40.5 kilometers
Therefore, Kaylee ran a total distance of 40.5 kilometers on those three days.
Bridges in Mathematics Grade 4 Student Book Unit 6 Module 2 Session 3 Answer Key
Work Place Instructions 6A Factors & Multiples
Each pair of players needs:
- 2 colored pencils of different colors
- 6A Factors & Multiples Record Sheet (1 copy to share)
1. Player 1 chooses a target number on the game board by drawing a circle around it. This number represents Player 1’s points for this round.
2. Using a different color, Player 2 circles all the numbers on the board that are factors of the target number, not including the target number itself. Player 2 adds these numbers together. The sum is Player 2’s points for this round.
For example, if Player 1 chooses 14 as a target number, Player 2 would circle 1, 2, and 7 because they are all factors of 14. So, Player 1 has 14 points and Player 2 has 10 points so far.
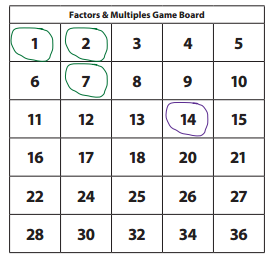
3. Then Player 2 chooses and circles a new target number and Player 1 circles all the numbers that are factors of that number. Once a number on the game board has been circled, it may no longer be used.
4. Players take turns choosing target numbers and circling factors.
If after completing a turn, a player realizes he missed a factor, he does not get to go back and cover that number.
5. When no further plays can be made, the game is over.
6. Each player then finds the sum of the numbers in her 6ircled squares. The player with the greater total is the winner.
Game Variations
A. A pair of players may play against another pair.
B. Players may create a game board that contains numbers greater than 36.
Answer:
Perimeter Problems
Use the perimeter and the known dimension to find the length of the missing dimension for each rectangle below. Show all your work.
Question 1.
Rectangle A
Perimeter = 72 feet
Dimension a = ____________ feet
Dimension b = 30 feet

Answer:
Dimension a = 72 feet
Explanation:
Given,
Perimeter = 2 (l + w)
Perimeter = 72 feet
We need to find l and b = 30 feet
72 = 2(l + 30)
72 = 2l + 60
12 = 2l
l = 12 ÷ 2
l = 6 feet
Question 2.
Rectangle B
Perimeter = 738 meters
Dimension a = 199 meters
Dimension b = ____________ meters
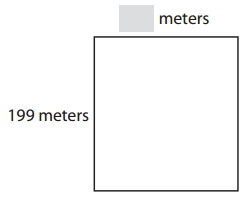
Answer:
Dimension b = 170 meters
Explanation:
Given,
Perimeter = 2 (l + w)
l = 199 m and and we need to find width
738 = 2 (199 + w)
738 = 398 + 2w
738 – 398 = 2w
340 = 2w
w = 340 ÷ 2
w = 170 meter
Question 3.
Rectangle C
Perimeter= 500 miles
Dimension a = 125 miles
Dimension b = ____________ miles
Make your own labeled sketch here.
Answer:
Dimension b = 125 miles
Explanation:
Given,
Perimeter = 2 (l + w)
500 = 2 (125 + w)
500 = 250 + 2w
500 – 250 = 2w
250 = 2w
w = 250 ÷ 2
w = 125 miles
Question 4.
Rectangle D
Perimeter= 129 yards
Dimension a = ______________ yards
Dimension b = 37 yards
Make your own labeled sketch here.
Answer:
Dimension a = 27.5 yards
Explanation:
Given,
perimeter = 2(l + w)
129 = 2(l + 37)
129 = 2l + 74
129 – 74 = 2l
55 = 2l
l = 55 ÷ 2
l = 27.5 yards.
Question 5.
CHALLENGE Rectangle E
Perimeter= 3,465 meters
Dimension a = 952 meters
Dimension b = _____________ meters
Make your own labeled sketch here.
Answer:
Dimension b = 780.5 meters
Explanation:
Given,
perimeter = 2(l +w)
3465 = 2(952 + w)
3465 = 1904 + 2w
1561 = 2w
w = 780.5 meters
Finding Factors & Multiples
Question 1.
Tell whether each of the following numbers is prime or composite.
a. 26 ____________
Answer:
The number 26 is a composite number.
Explanation:
To determine whether a number is prime or composite, we need to check if it has any factors other than 1 and itself. In the case of 26, we can find its factors by dividing it by numbers starting from 2 up to the square root of 26, which is approximately 5.1.
When we perform these divisions, we find that 26 is divisible by 2 and 13, in addition to 1 and itself. Since 26 has factors other than 1 and itself, it is considered a composite number.
b. 46 ____________
Answer:
The number 46 is a composite number.
Explanation:
To determine if a number is prime or composite by checking if it has factors other than 1 and itself.
In the case of 46, we can find its factors by dividing it by numbers starting from 2 up to the square root of 46, which is approximately 6.8. When we perform these divisions, we find that 46 is divisible by 2 and 23, in addition to 1 and itself. Since 46 has factors other than 1 and itself, it is considered a composite number.
c. 97 ____________
Answer:
The number 97 is a prime number.
Explanation:
To determine if a number is prime, we need to check if it has any factors other than 1 and itself. In the case of 97, we can find its factors by dividing it by numbers starting from 2 up to the square root of 97, which is approximately 9.8.
When we perform these divisions, we find that 97 is not divisible by any number other than 1 and itself. Therefore, 97 is only divisible by 1 and 97, making it a prime number.
d. 121 ____________
Answer:
The number 121 is a composite number.
Explanation:
To determine if a number is prime or composite, we check if it has any factors other than 1 and itself. In the case of 121, we can find its factors by dividing it by numbers starting from 2 up to the square root of 121, which is 11. When we perform these divisions, we find that 121 is divisible by 11, in addition to 1 and itself. Since 121 has factors other than 1 and itself, it is considered a composite number.
Question 2
Write all of the factor pairs for each of the following numbers.
a. 34
Answer:
1,34 and 17,2.
Explanation:
The factor pairs for number 34 is
1×34 = 34,
17×2 = 34.
b. 64
Answer:
1×64, 2×32, 4×16 and 8×8.
Explanation:
The factor pairs for number 64 is
1×64 = 64,
2×32 = 64,
4×16 = 64,
8×8 = 64.
c. 72
Answer:
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72.
Explanation:
The factor pairs for number 72 is
1×72 = 72,
2×36 = 72,
3×24 = 72,
4×18 = 72,
6×12 = 72,
8×9 = 72,
9×8 = 72,
12×6 = 72,
18×4 = 72,
24×3 = 72,
36×2 = 72,
72×1 = 72.
d. 79
Answer:
1×79.
Explanation:
The factor pairs for number 79 is 1×79.
Question 3.
Mandy was making a list of the multiples of 14. Which of the following lists is correct?
![]() 14, 28, 41, 55
14, 28, 41, 55
![]() 28, 42, 56, 74
28, 42, 56, 74
![]() 28, 42, 56, 70
28, 42, 56, 70
![]() 14, 28, 42, 66
14, 28, 42, 66
Answer:
28, 42, 56, 70.
Explanation:
The multiples of 14 are 28, 42, 56 and 70.
Question 4.
The area of a large rectangular rug is 54 square feet. List all the possible pairs of dimensions for the rug.
Answer:
The possible pairs of dimensions for the rectangular rug with an area of 54 square feet are:
1 foot by 54 feet
2 feet by 27 feet
3 feet by 18 feet
6 feet by 9 feet
Explanation:
The area of a rectangular rug is 54 square feet.
We can find the possible pairs of dimensions by finding all the factors of 54 and pairing them up.
We can start by finding the prime factorization of 54
54 = 2 × 3 × 3 × 3
Then we can use these prime factors to find all the factors of 54:
1, 2, 3, 6, 9, 18, 27, 54
1 × 54
2 × 27
3 × 18
6 × 9
Question 5.
Which of the following lists contains a number that is not a multiple of 7?
![]() 14, 28, 42, 56
14, 28, 42, 56
![]() 7, 14, 28, 35
7, 14, 28, 35
![]() 7, 21, 35, 64
7, 21, 35, 64
![]() 14, 21, 42, 56
14, 21, 42, 56
Answer:
The option 3. 7, 21, 35, 64 contains a number that is not a multiple of 7.
Explanation:
From the given options
the option 3 contains the number that is not multiple of 7.
The numbers are 7, 21, 35, 64
7 is multiple of 7.
21 is a multiple of 7.
35 is a multiple of 7.
64 is not a multiple of 7.
Bridges in Mathematics Grade 4 Student Book Unit 6 Module 2 Session 4 Answer Key
Work Place Instructions 6B Area or Perimeter
Each pair of players needs:
- 1 die numbered 1-6 and 1 die numbered 4-9
- 1 more/less die
- 1 spinner overlay to share
- 6B Area or Perimeter Record Sheets (1 for each player)
1. Players decide who will go first. One player rolls the more/less die to find out if they are playing for more or less.
2. Player 1 chooses Dimension Spinner A or B and spins to get one known dimension.
3. Then Player 1 rolls both dice, multiplies the numbers rolled, and decides whether he wants the product to be the perimeter or the area.
- The product of the roll has to be at least twice as much as the known dimension plus 2. For example, if a player spins a dimension of 6 and rolls 3 × 4 for a product of 12, he must roll again until he gets a product or 14 or higher.
- If the product is not a multiple of the known dimension, the player has to choose perimeter, not area. If the product is a multiple of the known dimension, the player can choose either perimeter or area.
4. Player 1 uses the known dimension and the perimeter or area to find the unknown dimension and records the information and work on his record sheet.
Players must record a labeled sketch and one or more equations to show how they found the missing dimension.
5. After Player 1 has determined the unknown dimension, Player 2 checks to see if the dimension is correct. Player 1 corrects the dimension, if necessary.
6. Then Player 2 takes a turn and repeats steps 3-6.
7. Players take three turns each. At the end of the game, players add the unknown dimensions they found during the game. If they rolled “less” on the more/less die, the player with a smaller sum wins the game. If they rolled “more” on the more/less die, the player with a larger sum wins.
Game Variations
A. Players can use 2 dice numbered 4-9.
B. Players who want to work with even larger products can use 2 dice numbered 4-9 and 1 die numbered 1-6, and multiply all 3 numbers they roll.
C. Instead of rolling the more/less die at the beginning of the game, players can set a target number for points and play until the first person reaches the target number. For example, if the target number is 50, players continue the game until one player’s unknown dimensions add up to 50 or more. If Player 1 reaches the target first, Player 2 gets one more turn to see if it’s a tie game.
D. Instead of rolling the more/less die at the beginning of the game, players can set a low target number and try to keep their final scores after three rounds below the target number. For example, if the target number is 10, players play three rounds and try to keep their scores under 10. The player with the lowest score wins.
Answer:
Area & Perimeter Challenges
Use labeled sketches and equations to model and solve each problem below. Show your work.
Question 1.
A rectangle has a perimeter of 84 meters. One dimension is 7 meters. How long is the unknown dimension?
Answer:
The length of the unknown dimension is 35 meters.
Explanation:
Given,
Perimeter of a rectangle is 84 meters.
The formula for the perimeter of a rectangle is 2 (length + width)
84 = 2 × l + 2 × 7
84 = 2l + 14
84 – 14 = 2l
70 = 2l
l = 70 ÷ 2
l = 35 meters.
Question 2.
If the perimeter of a rectangle is 24 cm and one dimension is 10 cm, what is the area?
Answer:
The area of the rectangle is 20 square cm.
Explanation:
The perimeter of the rectangle is 24 cm and one dimension is 10 cm
Perimeter = 2 (l + b)
24 = 2 × l + 2 × b
24 = 2 × l + 2 × 10
24 = 2l + 20
24 – 20 = 2l
4 = 2l
l = 4 ÷ 2
l = 2 cm
Area = 2 × 10
= 20 square cm
Question 3.
CHALLENGE A rectangle has an area of 243 square feet. One dimension is 9 feet. What is the length of the other dimension? Draw a sketch and show your work.
Answer:
The length of the other dimension of the rectangle is 27 feet.
Explanation:
Given,
Area of the rectangle is 243 square feet and one dimension is 9 feet
Area of the rectangle is length × width
243 = 9 × width
243 ÷ 9
27
The length of the other dimension of the rectangle is 27 feet.

Question 4.
CHALLENGE If the area of a rectangle is 36 square yards and one dimension is 12 yards, then what is the perimeter?
Answer:
Perimeter of the rectangle is 30 yards.
Explanation:
Given,
Area of the rectangle is 36 square yards.
one dimension is 12 yards.
Area of a rectangle is length × width
36 = l × w
l = 12
36 ÷ 12 = w
w = 3
Perimeter of the rectangle is 2 (l + b)
2(12) + 2(3)
24 + 6
30
The perimeter of the rectangle is 30 yards.
Bridges in Mathematics Grade 4 Student Book Unit 6 Module 2 Session 5 Answer Key
Frederico’s Fort
Frederico is building a tree fort. Help Frederico solve the work using numbers, sketches, or words.
Question 1.
The floor of the fort is 14 by 19 feet long. What is the area of the floor?
Answer:
Area of the floor of the fort is 266 square feet.
Explanation:
The floor of the fort is 14 by 19 feet long.
Area of the floor = length × width
Area = 14 × 19
area = 226 square feet
Area of the floor of the fort is 266 square feet.
Question 2.
Frederico has 2 windows in his fort. One window is 36 cm by 24 cm. The other window is 18 cm by 48 cm. Frederico says the area of both windows is the same. Do you agree or disagree? Why?
Answer:
Area of both windows combined = 54 cm x 72 cm = 3,888 square cm
Explanation:
Given,
Area of the first window
length × width
36 × 24 = 864 square cm
Area of the second window
18 × 48 = 864 square cm
The area of the both windows are same
Total length = 36 cm + 18 cm = 54 cm
Total width = 24 cm + 48 cm = 72 cm
Area of both windows = Total length × total width
area = 54 × 72
= 3888 square cm
Question 3.
The door of the fort is 55 inches by 28 inches. What is the area of the door?
Answer:
The area of the door of the fort is 1540 square inches.
Explanation:
Given,
Length = 55 inches
width = 28 inches
Area = length × width
= 1540 square inches
The area of the door of the fort is 1540 square inches.
Question 4.
Fill in the blanks.
a. 29 × 17 = (30 × 17) – (__________ × 17)
Answer:
The missing value is 1.
Explanation:
Let us solve the given equation
493 = 510 – 17x
17x = 510 – 493
17x = 17
x = 1
b. 32 × 16 = (30 × 10) + (30 × __________) + (2 × 10) + (__________ × __________)
Answer:
The missing values are 6, 2 and 8.
Explanation:
Let’s solve the equation step by step:
32 × 16 = (30 × 10) + (30 × ) + (2 × 10) + ( × __________)
First, let’s simplify the expressions on the right side of the equation:
32 × 16 = 300 + (30 × ) + 20 + ( × __________)
Next, we can fill in the missing values by solving the multiplication:
32 × 16 = 300 + (30 × 6) + 20 + (2 × 8)
32 × 16 = 300 + 180 + 20 + 16
32 × 16 = 516
Therefore, the equation can be simplified to:
516 = 516
c. 24 × 42 = 12 × ____________ = 6 × 168 = ___________ × 336
Answer:
The missing value is 84 and 3.
Explanation:
Let’s solve the equation step by step:
24 × 42 = 12 × ____________
1008 ÷ 12 = 84
Therefore 12 × 84 is equal to 24 × 42
6 × 168 = ___________ × 336
We can solve for the missing number by dividing both sides of the equation by 336
(6 × 168) ÷ 336 = (__ × 336) ÷ 336
1008 ÷ 336 = 3
Therefore 3 × 336 is equal to 6 × 168
Hence the missing values are 84 and 3.