Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 5 Module 2 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 5 Module 2
Bridges in Mathematics Grade 4 Student Book Unit 5 Module 2 Session 1 Answer Key
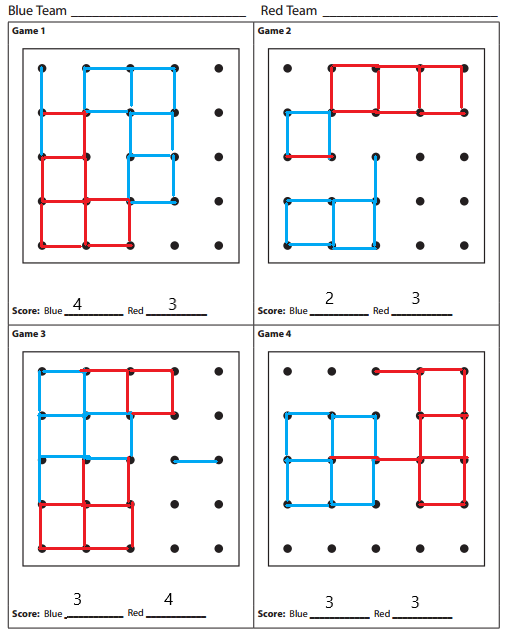
Dots & Lines Game Record Sheet
Answer:
Lines & Designs
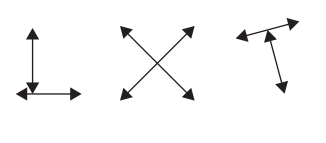
Question 1.
Fill in the bubbles in front of the words that describe each set of lines below. Then explain your answer. How do you know? The first one is done for you.
ex:
intersecting lines
parallel lines
perpendicular
How do you know?
These are intersect in lines because they cross. They are not perpendicular because they don’t cross at right angles.
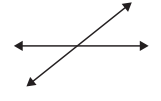
a.
intersecting lines
parallel lines
perpendicular
How do you know?
Answer:
Parallel lines.
Explanation:
Parallel lines are lines that do not intersect or meet each other at any point in a plane. Hence the given lines are parallel lines.
b.
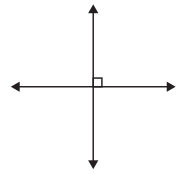
intersecting lines
parallel lines
perpendicular
How do you know?
Answer:
Perpendicular.
Explanation:
The perpendicular lines are two lines that intersect each other and the angle formed between the two lines should be equal to 90 degrees.
Question 2.
Get a geoboard and some colored rubber bands. Use them to make each of the designs described below. Then use regular and colored pencils to record your work on this sheet.
ex: Make a design with 6 gray parallel line segments.
a. Make a design with 6 red intersecting line segments.
Answer:
Explanation:
We have made a design with 6 red intersecting line segments. Check the figure.
Bridges in Mathematics Grade 4 Student Book Unit 5 Module 2 Session 2 Answer Key
Thinking About Lines
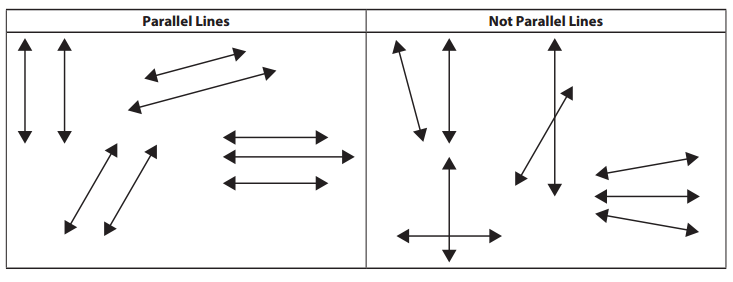
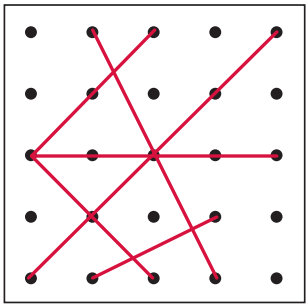
Question 1.
Study the diagram above. Use it to help answer the questions below.
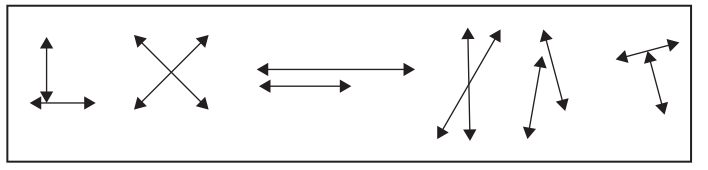
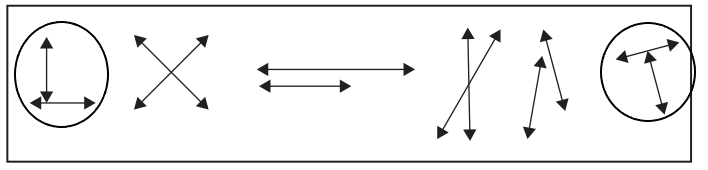
a. Circle all the examples of parallel lines in the box.
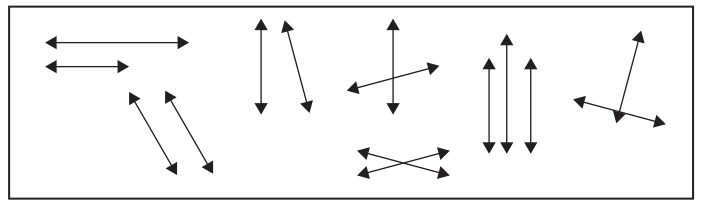
Answer:
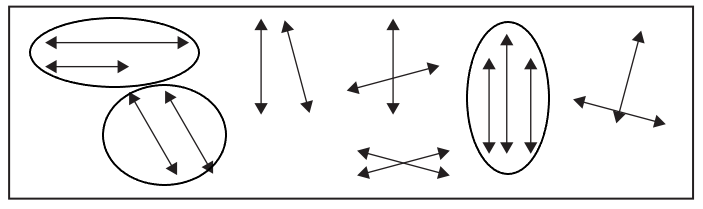
b. How do you know that the figures you circled are examples of parallel lines?
Answer:
Parallel lines are lines that do not intersect each other at any point in a line. Based on the definition given we can observe that the figures we circled are examples of parallel lines.
c. Draw 2 examples of parallel lines.
Answer:
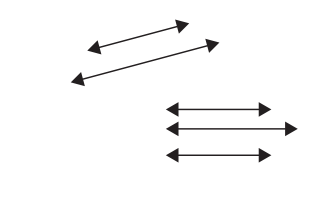
Explanation:
The two lines in the plane that are at an equal distance from each other and they never meet is called parallel lines. Therefore we have drawn 2 examples of parallel lines.
d. Draw 2 examples of lines that are not parallel.
Answer:
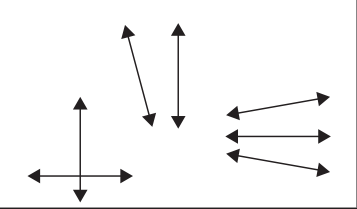
e. Write a definition for the term parallel lines.
Answer:
parallel lines are lines that are always the same distance and they never intersect.
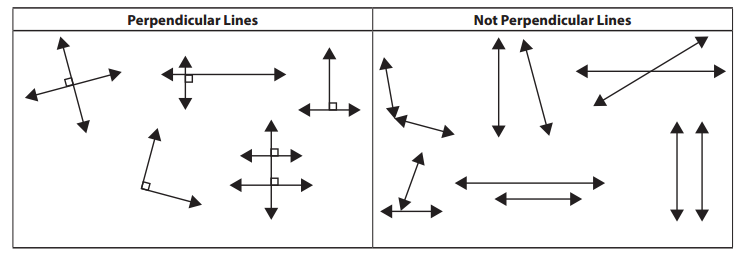
Question 2.
Study the diagram above.
a Circle all the examples of perpendicular lines in the box. (Hint: Use the corner of a piece of paper or a tile to check the angles.)
Answer:
Explanation:
We have circled all the examples of perpendicular lines in the box. Check the figure.
b. How do you know the figures you circled are examples of perpendicular lines?
Answer:
Perpendicular lines are lines that intersect each other at 90 degrees. Based on that we have figured out and circled are examples of perpendicular lines.
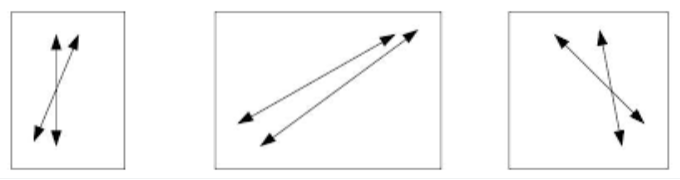
c. Draw 2 examples of perpendicular lines.
Answer:
Explanation:
I have drawn two examples of perpendicular lines.
d. Draw 2 examples of lines that are not perpendicular.
Answer:
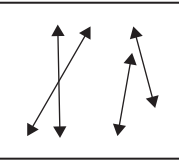
Explanation:
I have drawn two examples of lines that are not perpendicular.
e. Write a definition for the term perpendicular lines.
Answer:
Perpendicular lines are lines that intersect each other at 90 degrees.
Thinking About Triangles
Use the following information to help solve the problems below.
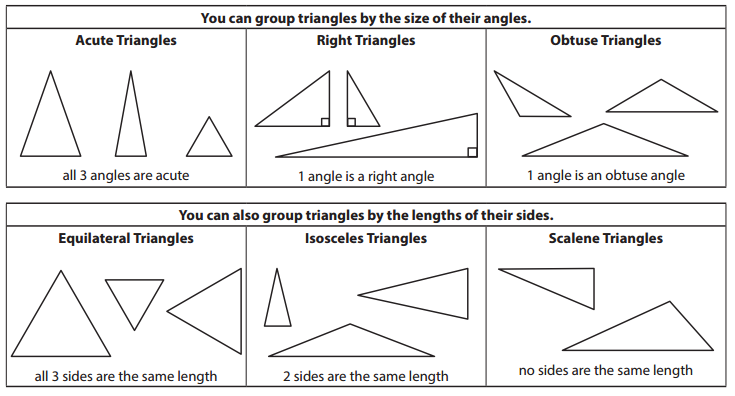
Question 1.
Fill in the bubble to show what kind of triangle each one is.
a.
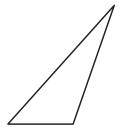
acute
right
obtuse
Answer:
The kind of triangle given in the figure is obtuse.
Explanation:
An obtuse-angled triangle is a triangle in which one of the interior angles measures more than 90 degrees.
b.
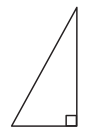
acute
right
obtuse
Answer:
The kind of triangle given in the figure is a right-angled triangle.
Explanation:
A right-angled triangle is a triangle in which one of the angles is 90 degrees.
c.
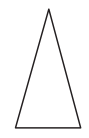
acute
right
obtuse
Answer:
The kind of triangle given in the figure is acute.
Explanation:
An angle that measures less than 90 degrees is called an acute angle.
d.
acute
right
obtuse
Answer:
The kind of triangle given in the figure is acute.
Explanation:
An angle that measures less than 90 degrees is called an acute angle.
e.
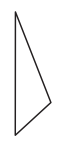
acute
right
obtuse
Answer:
The kind of triangle given in the figure is a right-angled triangle.
Explanation:
A right-angled triangle is a triangle in which one of the angles is 90 degrees.
f.
acute
right
obtuse
Answer:
The kind of triangle given in the figure is acute.
Explanation:
An angle that measures less than 90 degrees is called an acute angle.
Bridges in Mathematics Grade 4 Student Book Unit 5 Module 2 Session 3 Answer Key
Thinking About Line Symmetry
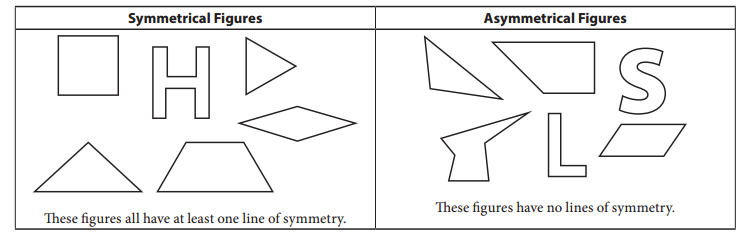
Question 1.
Study the diagram above. Use it to help answer the questions below.
a. Circle all the shapes below that have at least one line of symmetry. Use a colored pencil and a ruler to draw in the lines of symmetry on the shapes you circled.
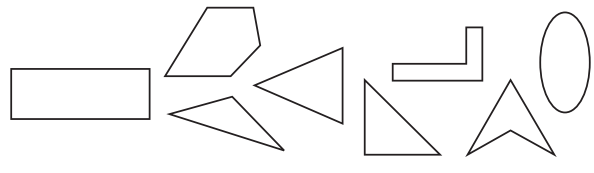
Answer:
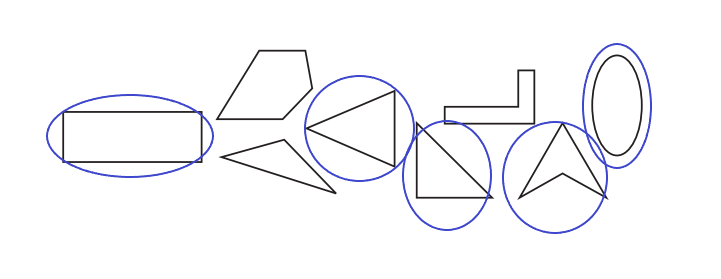
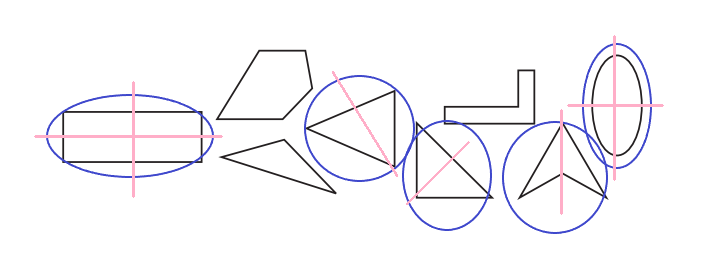
Explanation:
I have circled all the shapes below that have at least one line of symmetry. Also, I used a colored pencil and a ruler to draw the lines of symmetry on the shapes you circled.
b. Draw two shapes of your own that have at least one line of symmetry. Use a different color pencil to draw in the line(s) of symmetry on each.
Answer:
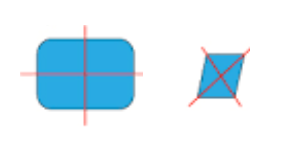
Explanation:
I have drawn two shapes that have one line of symmetry.
c. Draw two shapes of your own that have no lines of symmetry.
Answer:
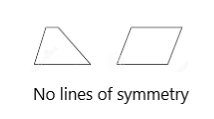
Explanation:
I have drawn two shapes that have no lines of symmetry.
d. Write a definition for the term line of symmetry.
Answer:
A line of symmetry is the line that divides a shape or object into two equal halves.
Work Place Instructions 5B Mosaic Game
Each pair of players needs:
- pattern blocks
- 1 die numbered 1-6
- 2 colored pencils
- 2 rulers
- 5B Mosaic Game Record Sheet for each player
1. Each player rolls the die. The player with the higher roll goes first.
2. The player rolls the die three times. For each roll, she takes a pair of pattern blocks. The Pattern Block Key on the record sheet shows which pair of pattern blocks to take for each number on the die.
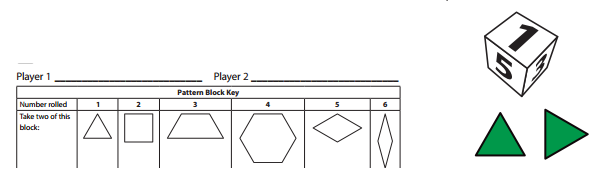
3. Then the player makes a design with the six pattern blocks. She gets a point for every line of symmetry in the design.
4. Both players—the one who made the design and her partner—sketch the design on their record sheets and draw in the line(s) of symmetry.
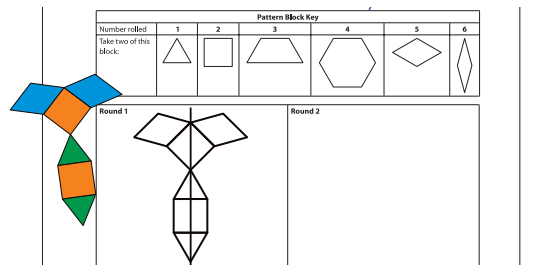
5. Players take turns until each player has gone twice. After two rounds, players add their total number of lines of symmetry.
6. The player with the higher total score wins.
Game Variations
A. Partners collaborate on a design and help each other find the lines of symmetry.
B. Players use the Mosaic Game Challenge page.
C. Players take 1 or 3 pattern blocks with each roll instead of 2, so they end up with a total of 3 or 9 blocks
instead of 6. What happens? Is it easier or harder to make symmetrical shapes with more or fewer pieces? Is it easier or harder to make symmetrical shapes with an odd number of pieces rather than an even number?
Answer:
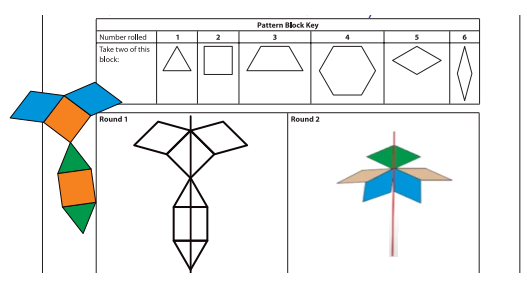
Pattern Block Symmetries
For each of the shapes below:
- Decide whether the shape has any lines of symmetry.
- Draw in all the lines of symmetry you can find.
Question 1.
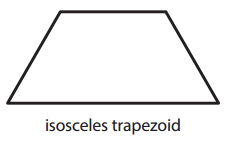
Answer:
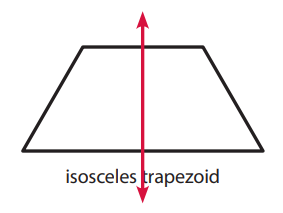
Explanation:
The given figure isosceles trapezoid has one line of symmetry.
Question 2.
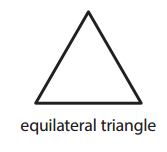
Answer:
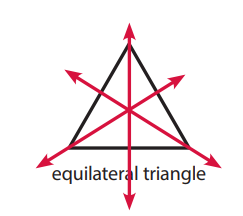
Explanation:
The given figure equilateral triangle has three lines of symmetry.
Question 3.
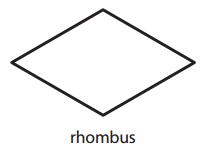
Answer:
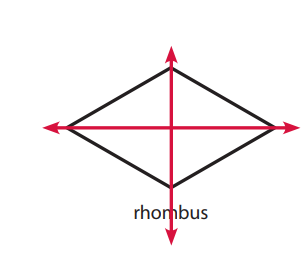
Explanation:
The given figure rhombus has two lines of symmetry.
Question 4.
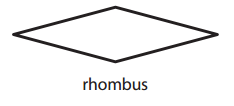
Answer:
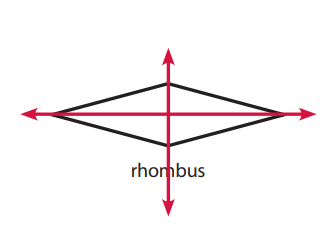
Explanation:
The given figure rhombus has two lines of symmetry.
Question 5.
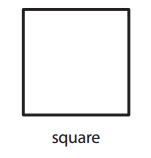
Answer:
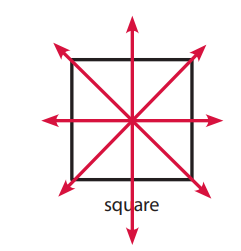
Explanation:
The given figure square has four lines of symmetry.
Question 6.
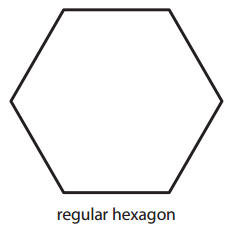
Answer:
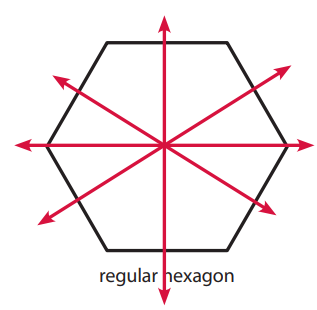
Explanation:
The given figure regular hexagon has four lines of symmetry.
Bridges in Mathematics Grade 4 Student Book Unit 5 Module 2 Session 4 Answer Key
Naming Polygons
Naming Polygons
A polygon is a closed two-dimensional figure made up of 3 or more line segments. The name of a polygon depends on how many sides it has.
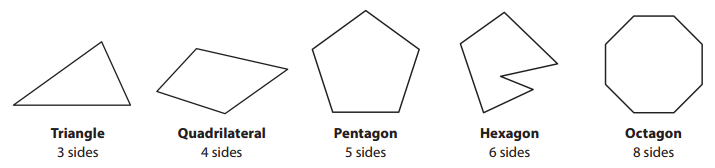
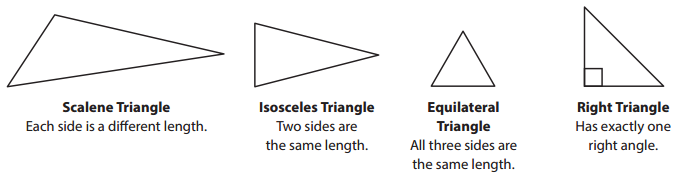
Naming Triangles
You can name a triangle by looking at its side lengths. You can also name a triangle by looking at its angles.
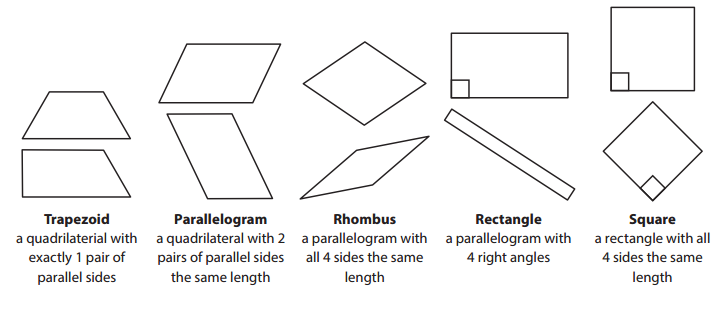
Naming Quadrilaterals
Any polygon with 4 sides is a quadrilateral, but some quadrilaterals have more than one name.
Drawing Shapes
Question 1.
Draw a shape with 5 sides and 1 right angle.
Answer:
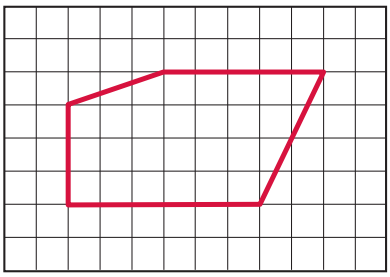
Question 2.
Draw a shape with only 2 parallel sides.
Answer:
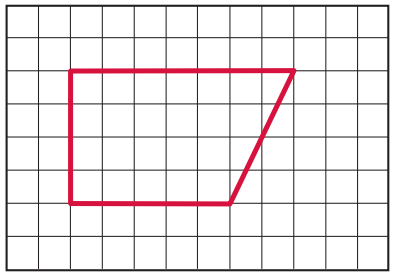
Question 3.
Draw a shape with 2 acute angles.
Answer:
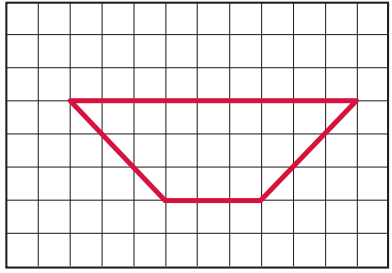
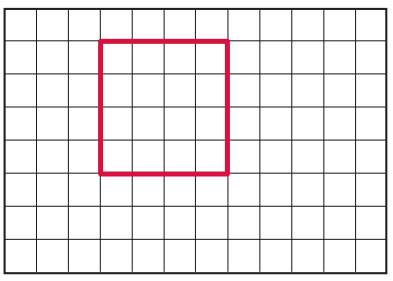
Question 4.
Draw a shape with only obtuse angles.
Answer:
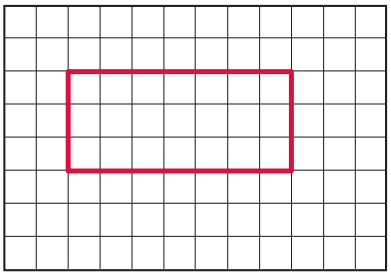
Question 5.
Draw a quadrilateral with 2 pairs of parallel sides.
Answer:
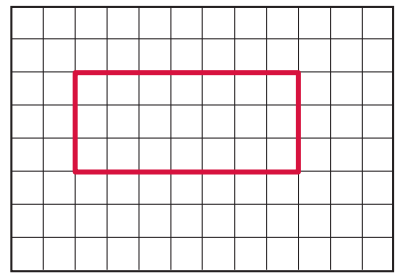
Question 6
Draw a quadrilateral with 4 congruent sides.
Answer:
Bridges in Mathematics Grade 4 Student Book Unit 5 Module 2 Session 5 Answer Key
Work Place Instructions 5C Solving Polygon Riddles
This is a one-player game. Each player needs:
- 3 or more polygon riddles
- 1 index card, 3 x 5 inches
- an envelope of polygon cards
- a 5C Polygon Riddles Record Sheet
1. The player spreads out all of the polygon cards.
2. The player chooses one polygon riddle and places it under an index card.
3. The player moves the index card just enough to see only the first clue, then turns all of the polygon cards that don’t fit the clue face-down.
4. The player continues to move the index card to reveal one clue at a time, turning polygon cards face¬down until only one remains face-up.
5. The player checks to make sure the polygon on the final polygon card matches all of the clues, then records the answer to that polygon riddle on the correct line of the record sheet.
6. After choosing another riddle and turning all of the polygon cards face-up, the player repeats steps 1-5. Players may solve as many riddles as time allows.
7. When time is up, the player collects the polygon cards into the envelope, then returns it and the riddles to the Work Place 5C tray.
The player keeps their Polygon Riddles Record Sheet in their Work Place folder.
Game Variations
A. Two players work as a team to solve each riddle. In that case, they use only one set of polygon cards.
B. A player writes polygon riddles to match some of the polygon cards in the set, then challenges a partner to solve them.
Answer:
Drawing Lines of Symmetry
ex:
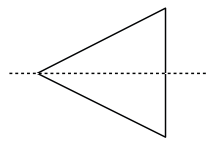
This figure has 1 line(s) of symmetry.
Question 1.
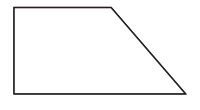
This figure has _______________ line(s) of symmetry.
Answer:
This figure has zero line(s) of symmetry.
Question 2.
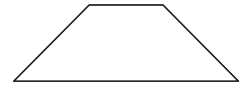
This figure has _______________ line(s) of symmetry.
Answer:
Explanation:
This figure has one line(s) of symmetry.
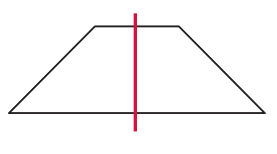
Question 3.
This figure has _______________ line(s) of symmetry.
Answer:
Explanation:
This figure has two lines of symmetry.
Question 4.
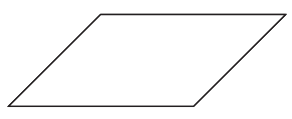
This figure has _______________ line(s) of symmetry.
Answer:
This figure has zero lines of symmetry.
Explanation:
The given figure does not have any lines of symmetry.
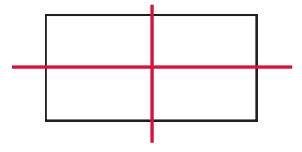
Question 5.
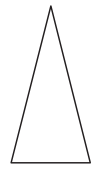
This figure has _______________ line(s) of symmetry.
Answer:
This figure has three lines (s) of symmetry.
Explanation:
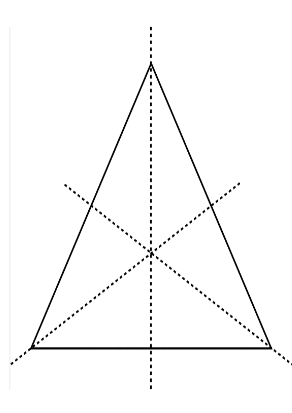
Question 6.
Complete each equation about angles.
a. 30° + _______________ = 180°
Answer:
150°.
Explanation:
Given,
30° + _______________ = 180°
Let us solve the given equation
30° + x = 180°
x = 180° – 30°
x = 150°
b. 4 × 90° = ________________
Answer:
360°
Explanation:
Given,
4 × 90°
let us solve the equation
4 × 90° = x
x = 360°
c. 270° – 180° = ______________
Answer:
90°
Explanation:
Given,
270° – 180°
Let us solve the equation
270° – 180° = x
90° = x
d. 90° ÷ _____________ = 30°
Answer:
3°
Explanation:
Given,
90° ÷ _____________ = 30°
Let us solve the given equation
90° ÷ x = 30°
90° ÷ 30° = x
x = 3°
Bridges in Mathematics Grade 4 Student Book Unit 5 Module 2 Session 6 Answer Key
Work Place Instructions 5D Polygon Bingo
Each pair of players needs:
- 1 set of polygon cards
- 5D Polygon Bingo Record Sheets for each player
- 2 Polygon Bingo Game Boards
- 30 game markers
1. Players shuffle the polygon cards and place them face-down in a stack.
2. Each player chooses a different Polygon Bingo Game Board to use.
3. Player 1 selects a card and reads the shape name aloud.
4. Player 1 draws the polygon on his record sheet and writes its name below the drawing. Player 2 verifies that the drawing and name are correct.
Player 2 That looks right. Your rhombus has 4 sides and they’re all the same length.
5. Then Player 1 finds an attribute that describes the shape on the Polygon Bingo Game Board and places a game marker on it. Player 2 verifies that the shape has the attribute described.
Player 1 I made a rhombus. That has all equal sides. I can cover that one.
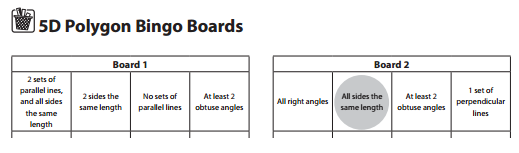
6. Play continues, with players taking turns repeating steps 3, 4, and 5.
7. The game continues until o ne player has covered a complete line of’ b oxes (horizontal, vertical, or diagonal) on the game board. If Player 1 is the first player to c omplete a line, Player 2 can take one more turn to see if she can also complete a line and make it a tie game.
Game Variation
A. Players try to cover the entire game board.
Answer:
Classifying Triangles & Quadrilaterals
Question 1.
All of the triangles in the box have something in common. Fill in the circle next to the triangle that belongs with them.
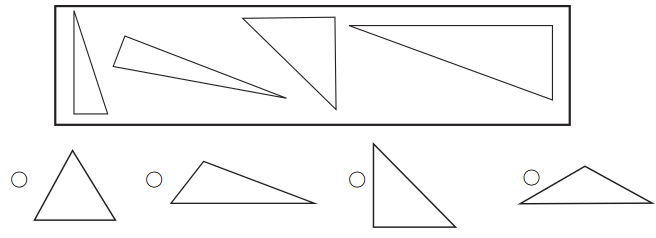
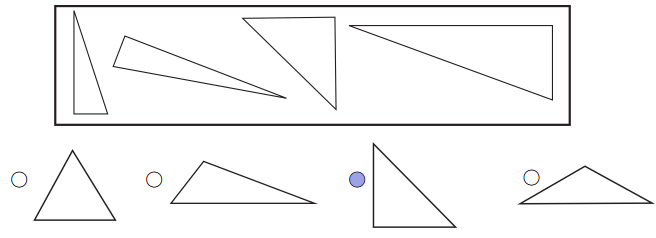
a. How do you know the triangle you picked belongs in the group?
Answer:
It has a right angle.
Explanation:
From the given triangle we can see that all triangles given in the figure are right angles triangles. Based on that we can pick option c traingle.
b. What is the name for this kind of triangle?
Answer:
Right triangle.
Explanation:
The name for this kind of triangle is a right triangle because it has 90°
Question 2.
All of the quadrilaterals in the box have something in common. Fill in the circle next to the quadrilateral that belongs with them.
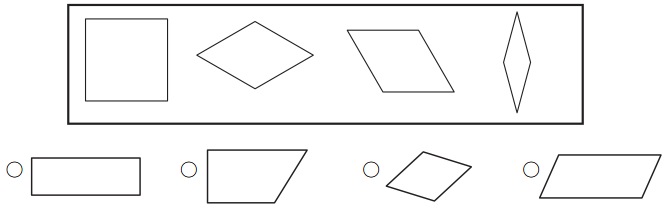
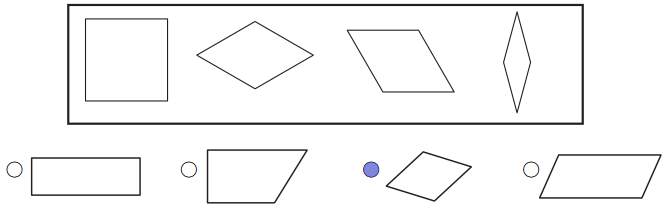
a. How do you know the quadrilateral you picked belongs in the group?
Answer:
It has 2 pairs of parallel sides and all 4 sides are the same length.
Explanation:
In the given figure all the quadrilaterals have 2 pairs of parallel sides and all 4 sides are the same length.
b. What is the name for this kind of quadrilateral?
Answer:
Rhombus.
Explanation:
The name for this kind of quadrilateral is a rhombus that has 2 pairs of parallel sides and all 4 sides are the same length.