Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 2 Module 1 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Student Book Answer Key Unit 2 Module 1
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 1 Session 1 Answer Key
Place Value & The Great Wall
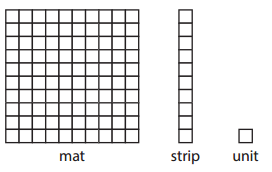
Take a look at the Great Wall of Base Ten you just made with your classmates, and fill in the table below to see how these pieces relate to each other.

Base Ten Area Pieces
Write and solve an equation for each problem below.
Question 1.
Max has 5 strips. How many units are in Max’s strips in all? _________
Answer:
Given,
Max has 5 strips.
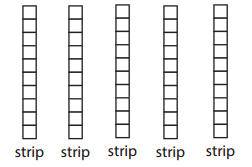
A strip has 10 units.
5 strips has 5 × 10 = 50 units.
Thus there are 50 units in Max’s strips.
Question 2.
Amelia has 10 times as many strips as Max.
a. How many strips does Amelia have? ______
Answer:
Max has 5 strips.
Amelia has 10 times as many strips as Max.
10 × 5 = 50 strips
Thus Amelia have 50 strips.
b. How many units are in Amelia’s strips in all? _____
Answer:
A strip has 10 units.
50 strips has 50 × 10 = 500 units.
Thus there are 500 units in Amelia’s strips.
c. How many mats can Amelia make with her strips? ___
Answer:
A mat has 10 strips.
Amelia have 50 strips.
Amelia can make 5 mats with her strips.
Question 3.
Leon has 8 strips. How many units are in Leon’s strips in all? _________
Answer:
Given,
Leon has 8 strips.
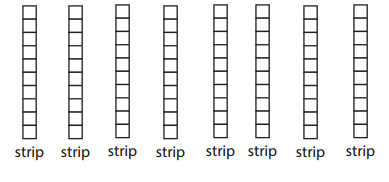
A strip has 10 units.
8 strips has 8 × 10 = 80 units.
Thus there are 80 units in Leon’s strips.
Question 4.
Zia has 100 times as many strips as Leon.
a. How many strips does Zia have? _______
Answer:
Given,
Zia has 100 times as many strips as Leon.
Leon has 8 strips.
8 × 100 = 800 strips.
Thus Zia have 800 strips.
b. How many units are in Zia’s strips in all? ________
Answer:
A strip has 10 units.
800 × 10 = 8000 units
Thus there are 8000 units in Zia’s strips.
c. How many mats can Zia make with her strips? ______
Answer:
A mat has 10 strips.
Zia have 800 strips.
800/10 = 80 mats.
Zia can make 80 mats with her strips.
d. How many strip-mats can Zia make with her strips? _________
Answer:
Zia can make 80 mats with her strips.
Question 5.
Sage has 3 strip-mats, 3 mats, and 2 units. Tristan has 2 mats, 8 strips, and 5 units. Andre has twice as many strip-mats, mats, and units as Sage.
a. How many units is that in all? Show your work.
Answer:
Sage has 3 strip-mats, 3 mats, and 2 units.
Tristan has 2 mats, 8 strips, and 5 units.
Andre has twice as many strip-mats, mats, and units as Sage.
Total = Sage + Tristan + Andre
Sage has 2 units
Tristan has 5 units
Andre’s number of units would be 4.
Total = 2 + 5 + 4 = 11
Thus there are 11 units in all.
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 1 Session 2 Answer Key
Multiplicative Comparisons on the Wall
You’ll need to be able to see the Great Wall of Base Ten in your classroom to complete parts of this sheet.
Question 1.
Here are the three smallest pieces on the Great Wall: the unit, the strip, and the mat. Use them to help answer problems a-c below.
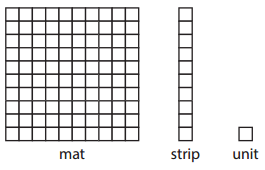
a. Fill in the blanks below.
The strip is _____ times as big as the unit.
The mat is ____ times as big as the strip.
Answer:
The strip is 10 times as big as the unit.
The mat is 10 times as big as the strip.
b. Andrew says that the mat is 1,000 times as big as the unit. Do you agree? Why or why not?
Answer:
Given,
Andrew says that the mat is 1,000 times as big as the unit.
A mat has 100 units.
100 < 1000
So I don’t agree with Andrew.
c. Which equation tells how many times bigger the mat is than the strip?
![]() 1 × 100 = 100
1 × 100 = 100
![]() 100 = 10 × 10
100 = 10 × 10
![]() 100 = 10 + 10
100 = 10 + 10
Answer:
A mat has 100 units.
10 × 10 = 100 units
100 = 10 × 10
Option B is the correct answer.
Question 2.
Now look at all the pieces on the Great Wall of Base Ten in your classroom. Fill in the blanks to complete these statements of multiplicative comparison.
a. The strip-mat is ____ times as big as the mat.
Answer: The strip-mat is 10 times as big as the mat.
b. The mat-mat is 100 times as big as the ____.
Answer: The mat-mat is 100 times as big as the unit.
c. The strip-mat is ____ times as big as strip.
Answer: The strip-mat is 10 times as big as strip.
Question 3.
In the number 222, the 2 in the hundreds place is worth ____ times as much as the 2 in the tens place.
Answer:
In the number 222, the 2 in the hundreds place is worth 100 times as much as the 2 in the tens place.
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 1 Session 3 Answer Key
Finding Areas of Rectangles
Question 1.
Measure and label the dimensions of both rectangles in centimeters. Then find the area of each in square centimeters. Show your work
a.

Answer:
L = 10 cm
W = 7 cm
We know that,
Area of the rectangle = l × w
A = 10 × 7 = 70 sq. cm
b.
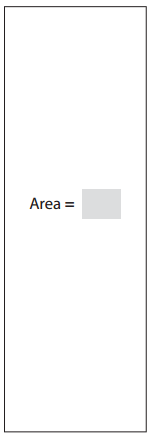
Answer:
l = 3 cm
w = 10 cm
We know that,
Area of the rectangle = l × w
A = 3 × 10 = 30 sq. cm
Question 2.
Measure the dimensions of this page to the nearest whole centimeter. Use the information to determine the area of the page. Label each measurement with the correct units.
Work space:
Length of the page: ______
Width of the page: ____
Area of the page: _____
Answer:
Length of the page = 14 cm
Width of the page = 18 cm
We know that,
Area of the rectangle = l × w
A = 14 × 18
A = 252 sq. cm
Question 3.
How would you find the area of the floor of our classroom? What units would you use? Draw a sketch and explain your thinking in the space below.
Answer:
L = 9 m
W = 8 m
We know that,
Area of the rectangle = l × w
A = 9 × 8 = 72 sq. m
Thus the area of the floor of our classroom is 72 sq. m
Nick is moving to a new house. His new room is smaller than his room where he used to live. Nick is using a meter stick to measure several items to see if they will fit in his new room.
Question 1.
Nick is measuring the length of his bed. What unit should Nick use? ______
Answer:
Given,
Nick is measuring the length of his bed.
We can measure the length of the bed in foot.
The length of the bed is 6 feet.
Question 2.
Nick is measuring the width of his mp3 player. What unit should Nick use? _____
Answer:
Given,
Nick is measuring the width of his mp3 player.
The width of the mp3 player cab be measured in inches.
Question 3.
Nick is measuring the height of his chair. What unit should Nick use? _____
Answer:
Given,
Nick is measuring the height of his chair.
The height of the chair can be measured in inches.
Question 4.
Nick has a rug that is 12 decimeters by 18 decimeters. Draw a small, labeled sketch of Nick’s rug. Then, find the area of his rug in square decimeters.
Write an equation that shows the area of the rug: ______
Answer:
Given,
Nick has a rug that is 12 decimeters by 18 decimeters.
Area of the rectangle = l × w
A = 12 × 18 = 216 sq. decimeters
Thus the area of his rug is 216 square decimeters
Question 5.
There is a window in Nick’s new room that is 11 decimeters by 15 decimeters. Draw a small, labeled sketch of the window. Then, find the area of the window in square decimeters.
Write an equation that shows the area of the window: _________
Answer:
Given,
There is a window in Nick’s new room that is 11 decimeters by 15 decimeters.
Area of the rectangle = l × w
A = 11 × 15 = 165 sq. decimeters.
Thus the area of the window is 165 square decimeters.
Question 6.
The back of Nick’s bookcase measures 10 decimeters by 18 decimeters. Nick thinks its area is 108 square decimeters. Do you agree? Use numbers, labeled sketches, or words to explain your answer.
Answer:
Given,
The back of Nick’s bookcase measures 10 decimeters by 18 decimeters.
Nick thinks its area is 108 square decimeters.
Area of the rectangle = l × w
A = 10 × 18 = 180
Yes, I agree with Nick.
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 1 Session 4 Answer Key
Work Place Instructions 2A What’s Missing? Bingo
Each pair of players needs:
- 2 What’s Missing? Bingo Record Sheets
- a deck of What’s Missing? Bingo Cards to share
1. Each player chooses one of the bingo boards on their own record sheet.
Players need to choose different boards.
2. Players decide who will go first, shuffle the cards, and place them in a stack face-down.
3. Players take turns drawing a card from the top of the stack and then work together to determine what the missing number is.
Sage Hmm … this means that something times 7 is 35. What times 7 is 35?
Nicole I remember! It’s 5.

4. Both players mark an X over the missing number if it appears on their bingo board. Some numbers may appear more than once, so players should think carefully about where they mark the X. (A player can only mark one number on each turn, even if there are 2 or more of the same number on the board.)
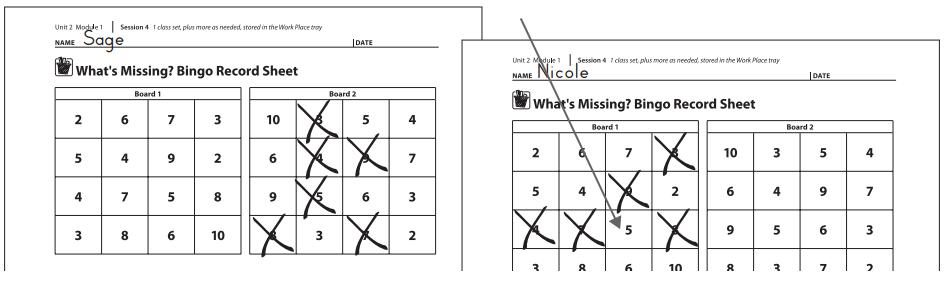
Nicole There are two 5s on my board, but if I put my × here, I can get 4 in a row and win!
5. Players continue to take turns drawing cards and marking their boards until one of them gets 4 in a row, horizontally, vertically, or diagonally.
Game Variations
A. Play the game more than once. Since both players have 4 boards on their sheets, they can play up to 4 times in a single session, as long as they choose a different board than their partner each time.
B. Play for blackout instead of 4 in a row. (Blackout is when one player marks off every number on his or her bingo board.)
C. Play with two boards instead of one. (Players can still mark only one number per turn, but in playing this version of the game, they can move between the two boards, switching from one to the other whenever they want.) The first player to get 4 in a row on both boards wins.
Be sure each player chooses the 2 boards his or her partner is not using. For example, Player 1 might use Boards 1 and 4, while Player 2 uses Boards 2 and 3.
Flora Tries Again
After Flora found that the piece of cloth she’d cut wasn’t big enough, she tried again several times to cut a piece that was exactly 240 square centimeters. Here are the dimensions of the four other rectangles she cut.

Question 1.
Circle the combination you believe will produce a piece of cloth closest to the size Flora needs.
Answer:
Given,
After Flora found that the piece of cloth she’d cut wasn’t big enough, she tried again several times to cut a piece that was exactly 240 square centimeters.

230 sq. cm is close to 240 square centimeters.
So, the answer is 240 sq. cm.
Question 2.
Create a rectangular array with base ten area pieces to model each of the combinations.
Answer:
Each strip has 8 units.
10 × 8 = 80 sq. cm

10 × 12 = 120 sq. cm
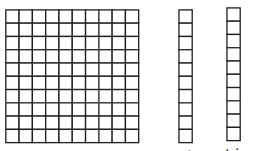
10 × 15 = 150
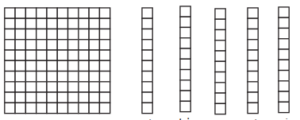
10 cm × 23 cm
= 230 sq. cm
Question 3.
For each combination, find the area of the piece of cloth Flora cut. Record your answers below, and be sure to label them with the proper units.
a. 10 cm × 8 cm = _____
Answer:
10 cm × 8 cm
= 800 sq. cm
b. 10 cm × 12 cm = ____
Answer:
10 cm × 12 cm
= 120 sq. cm
c. 10 cm × 15 cm = ____
Answer:
10 cm × 15 cm
= 150 sq. cm
d. 10 cm × 23 cm = _____
Answer:
10 cm × 23 cm
= 230 sq. cm
Question 4.
CHALLENGE Can you think of more than one way for Flora to cut a rectangle that is exactly 240 square centimeters?
Answer:
240 can be written as 24 × 10
length = 24 cm
width = 10 cm
Area = 24 × 10 = 240 square centimeters
Arrays & Equations for Tens
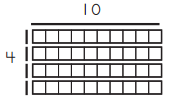
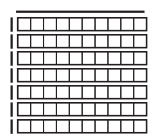
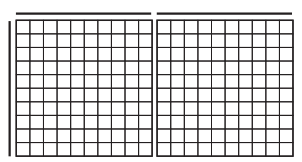
Question 1.
For each rectangle below, label the dimensions, find the area, and write a multiplication equation to describe the array.
ex
Labeled Array
Area
40
Multiplication Equation
4 × 10 = 40
a.
Labeled Array
Area
Multiplication Equation
Answer:
10 × 7
Area = 10 × 7 = 70
Multiplication Equation:
10 × 7 = 70
b.
Labeled Array
Area
Multiplication Equation
Answer:
Area = 10 × 10 + (10 × 10)
= 100 + 100 = 200 sq. units
Multiplication Equation:
(10 × 10) + (10 × 10) = 200
c.
Labeled Array
Area
Multiplication Equation
Answer:
Area = (10 + 5) × 10
= 15 × 10
= 150 sq. units
Multiplication Equation:
15 × 10 = 150
Question 2.
Complete the multiplication facts below.
10 × 4 = ____ 10 × 2 = ____ 10 × 9 = ____
10 × 3 = ____ 10 × 5 = ____ 10 × 8 = ____
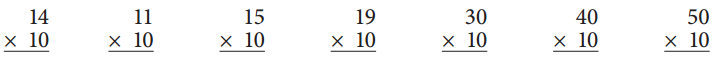
Answer:
10 × 4 = 40
10 × 2 = 20
10 × 9 = 90
10 × 3 = 30
10 × 5 = 50
10 × 8 = 80
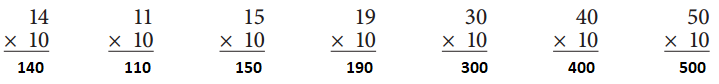
Question 3.
What happens every time you multiply a number by 10? Why?
Answer: When you multiply a number by 10, the value of each digit becomes ten times bigger, so each digit moves one place to the left.
Bridges in Mathematics Grade 4 Student Book Unit 2 Module 1 Session 5 Answer Key
Multiplication Arrays
Build each array below. Then write an expression or equation to show how you found the product, and record the product in the last column.
Question 1.
Build This Array
14 × 11
Expression or Equation Product
Product
Answer:
14 × 11 = 154
Question 2.
Build This Array
11 × 16
Expression or Equation Product
Product
Answer:
11 × 16 = 176
Question 3.
Build This Array
15 × 21
Expression or Equation Product
Product
Answer:
15 × 21 = 315
Question 4.
Build This Array
12 × 16
Expression or Equation Product
Product
Answer:
12 × 16 = 192
Question 5.
Write a story problem to match one of the combinations above.
Answer:
Question 6.
CHALLENGE The perimeter of Square A is 24 linear units. The area of Square B is 4 times the area of Square A. What is the area of Square B? What is the perimeter of Square B? Show your work.
Answer:
Given,
The perimeter of Square A is 24 linear units. The area of Square B is 4 times the area of Square A.
24 = 4L
L = 24/4 = 6 linear units
Area of the square = s²
A = 6 × 6 = 36 sq. units
The area of Square B is 4 times the area of Square A.
Area of Square B = 4 × Area of Square A
Area of Square B = 4 × 36
So, Area of Square B = 144 Quadratic Units
Area = s²
s = √area
s = √144
s = 12 linear units
Perimeter = 4s
= 4 × 12
= 48 linear units
Fill the Frames
Label each array frame below. Then fill it in with labeled rectangles. Write an addition equation to show how you got the total. Then write a multiplication equation to match the array.
ex
Labeled Array Frame & Rectangle
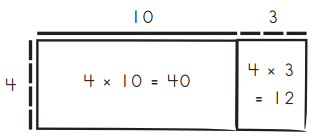
Addition Equation
40 + 12 = 52
Multiplication Equation
4 × 13 = 52
Question 2.
Labeled Array Frame & Rectangle

Addition Equation
Multiplication Equation
Answer:
Addition Equation:
40 + 20 = 60
Multiplication Equation:
4 × 15 = 60
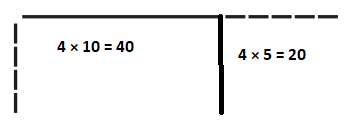
Question 3.
Labeled Array Frame & Rectangle

Addition Equation
Multiplication Equation
Answer:
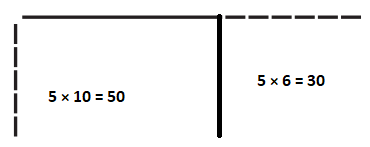
Addition Equation:
50 + 30 = 80
Multiplication Equation:
5 × 16 = 80