Practicing the Bridges in Mathematics Grade 4 Home Connections Answer Key Unit 3 Module 2 will help students analyze their level of preparation.
Bridges in Mathematics Grade 4 Home Connections Answer Key Unit 3 Module 2
Bridges in Mathematics Grade 4 Home Connections Unit 3 Module 2 Session 2 Answer Key
Brownie Dessert
A fourth grade class earned a brownie dessert party for having the highest attendance in one grading period. Small pans of brownies were cut into 9 pieces, and large pans were cut into 16 pieces.
Question 1.
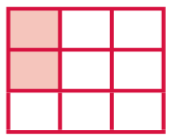
Tori ate 2 brownies from a small pan. What fraction of the brownies in that pan did she eat? Draw a sketch to show your thinking.
Answer:
\(\frac{2}{9}\).
Explanation:
She ate \(\frac{2}{9}\) fraction of the brownies in that pan.
Question 2.
Holly ate 1 more brownie than Tori from the same small pan. Write two equivalent fractions that describe how much Holly ate.
Answer:
\(\frac{3}{9}\) and \(\frac{1}{3}\).
Explanation:
The two equivalent fractions that describe how much Holly ate are \(\frac{3}{9}\) and \(\frac{1}{3}\).
Question 3.
Henry’s table group seats 5 students. Each student ate 2 brownies from a large pan. Write an equation that shows what fraction of a large pan of brownies was eaten at Henry’s table.
Answer:
\(\frac{10}{16}\)
Explanation:
Given,
Henry’s table group seats 5 students.
Each student ate 2 brownies from a large pan
5 × \(\frac{2}{16}\)
\(\frac{10}{16}\)
Question 4.
April ate 1 brownie from a large pan, and her friend, Christina, ate 4 brownies from the same pan.
a. Write two fractions to tell how much of the large pan of brownies Christina ate.
Answer:
\(\frac{4}{16}\) and \(\frac{1}{4}\) or \(\frac{2}{8}\).
Explanation:
The two fractions are \(\frac{4}{16}\) and \(\frac{1}{4}\) or \(\frac{2}{8}\) will tell how much of the large pan of brownies Christina ate.
b. What fraction of a large pan of brownies did the girls eat together?
Answer:
\(\frac{5}{16}\)
Explanation:
The fraction of \(\frac{5}{16}\) of a large pan of brownies did the girls eat together.
Brownie Dessert
Question 1.
Freddy had 2 of the brownies from a large pan. His friend said he ate 1 of the brownies in that pan. Tell why you agree or disagree.
Answer:
Yes, I agree.
Explanation:
Given,
Freddy had 2 of the brownies from a large pan.
His friend said he ate 1 of the brownies in that pan
2 – 1 = 1
Hence We can agree that his friend said he ate 1 of the brownies in that pan
Question 2.
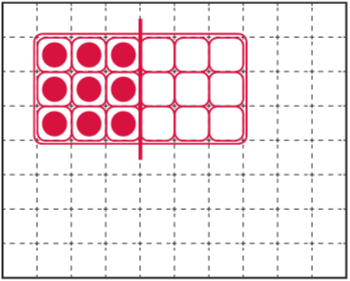
CHALLENGE In an 18-egg carton, \(\frac{1}{3}\) equals 6 eggs. Use the grids below to help you imagine and draw cartons where:
a. \(\frac{1}{3}\) is 9 eggs.

Answer:
There are 9 eggs given and we used the grids below and drew the cartons.
Explanation:
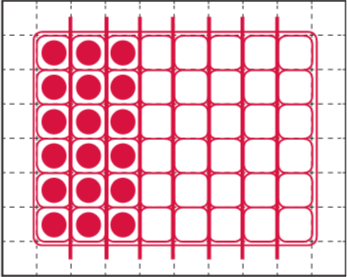
b. \(\frac{3}{8}\) is 18 eggs.

Answer:
There are 18 eggs given and we used the grids below and drew the cartons.
Explanation:
Bridges in Mathematics Grade 4 Home Connections Unit 3 Module 2 Session 4 Answer Key
Planning a Garden
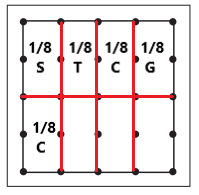
The Brown family is trying to decide how to plan their garden for the vegetables they want to grow. Use the geoboard model to design a garden that fits each description. Label every area to show where each vegetable will be planted.
Question 1.
The Browns could plant \(\frac{1}{2}\) tomatoes, \(\frac{1}{4}\) squash, and \(\frac{1}{4}\) lettuce.
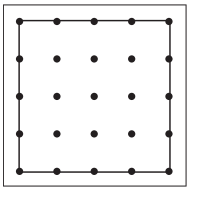
Answer:
I have labeled every area to show where each vegetable is to be planted.
Explanation:
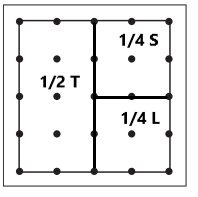
Question 2.
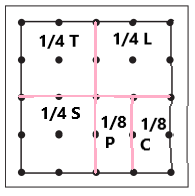
They could plant \(\frac{1}{4}\) tomatoes, \(\frac{1}{4}\) squash, \(\frac{1}{4}\) lettuce, \(\frac{1}{8}\) peppers, and \(\frac{1}{8}\) cabbage.
Answer:
I have labeled every area to show where each vegetable is to be planted.
Explanation:
Question 3.
The Brown family might plant \(\frac{1}{8}\) tomatoes, \(\frac{1}{8}\) cabbage, and \(\frac{1}{8}\) peppers. If they do, what fraction of their garden will be unplanted?
Answer:
The fraction \(\frac{5}{8}\) of their garden will be unplanted.
Explanation:
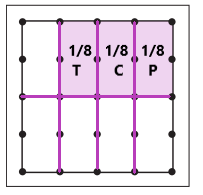
Planning a Garden
Question 1.
If the Browns plant \(\frac{3}{16}\) tomatoes, \(\frac{1}{4}\) cabbage, and \(\frac{2}{8}\) peppers, what fraction of their garden will be unplanted?
Answer:
The fraction \(\frac{5}{16}\) of their garden is to be unplanted.
Explanation:
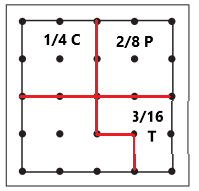
Question 2.
CHALLENGE Create a plan for a garden that has room for 5 different vegetables. Label the vegetables in the garden and write a equation to represent the model.
Answer:
I have created a plan for a garden that has room for 5 different vegetables. And labeled the vegetables in the garden and write a equation to represent the model.
Explanation:
Bridges in Mathematics Grade 4 Home Connections Unit 3 Module 2 Session 6 Answer Key
Fractions & More Fractions
Question 1.
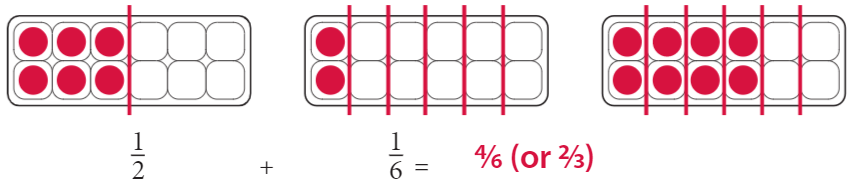
Ethan used an egg carton model to add fractions. Draw eggs in the cartons to show and solve the problem. Then fill in the blank to show the answer.
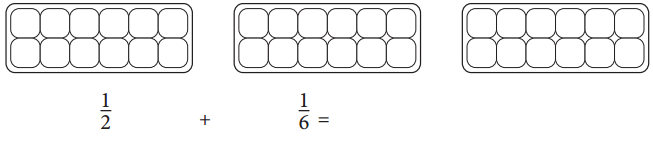
Answer:
I have drawn eggs in the cartons and solved the problem. I also have filled in the blank to show the answer.
Explanation:
Question 2.
Put the following numbers in order on the number line below.

Answer:
I have put the following numbers in order on the number line below.
Explanation:

Question 3.
Maria is writing as many different addition and multiplication equations as she can for 2 \(\frac{2}{8}\). Her rule is that all the fractions in each equation must have a denominator of 8.
a. Here are the equations Maria has written so for. Fill in the bubble beside each equation that is true.
![]() 2\(\frac{2}{8}\) = 1 + 1 + \(\frac{2}{8}\)
2\(\frac{2}{8}\) = 1 + 1 + \(\frac{2}{8}\)
![]() 2\(\frac{2}{8}\) = \(\frac{8}{8}\) + \(\frac{10}{8}\)
2\(\frac{2}{8}\) = \(\frac{8}{8}\) + \(\frac{10}{8}\)
![]() \(\frac{5}{8}\) + \(\frac{5}{8}\) + \(\frac{5}{8}\) + \(\frac{4}{8}\) = 2\(\frac{2}{8}\)
\(\frac{5}{8}\) + \(\frac{5}{8}\) + \(\frac{5}{8}\) + \(\frac{4}{8}\) = 2\(\frac{2}{8}\)
![]() 18 × \(\frac{1}{8}\) = 2\(\frac{2}{8}\)
18 × \(\frac{1}{8}\) = 2\(\frac{2}{8}\)
Answer:
The equations that are true
2\(\frac{2}{8}\) = 1 + 1 + \(\frac{2}{8}\), 2\(\frac{2}{8}\) = \(\frac{8}{8}\) + \(\frac{10}{8}\) and 18 × \(\frac{1}{8}\) = 2\(\frac{2}{8}\).
Explanation:
2\(\frac{2}{8}\) = 1 + 1 + \(\frac{2}{8}\)
= \(\frac{(8 + 8 + 2}{8}\)
\(\frac{18}{8}\) = \(\frac{18}{8}\)
Check the next option
2\(\frac{2}{8}\) = \(\frac{8}{8}\) + \(\frac{10}{8}\)
= \(\frac{(8 + 10)}{8}\)
= \(\frac{10}{8}\)
18 × \(\frac{1}{8}\) = 2\(\frac{2}{8}\)
\(\frac{18}{8}\) = 2\(\frac{2}{8}\)
b. Write at least four more addition or multiplication equations for 2\(\frac{2}{8}\) in which all the fractions have a denominator of 8.
Answer:
We have written four more addition or multiplication equations.
Explanation:
\(\frac{8}{8}\) + \(\frac{8}{8}\) + \(\frac{2}{8}\) = 2\(\frac{2}{8}\)
2 × \(\frac{9}{8}\) = 2\(\frac{2}{8}\)
9 × \(\frac{2}{8}\) = 2\(\frac{2}{8}\)
3 × \(\frac{6}{8}\) = 2\(\frac{2}{8}\)
Question 4.
Calvin and Leah are playing a game that has them draw fraction cards to add up to numbers that fill a 12-egg carton. Calvin had \(\frac{1}{3}\) of his egg carton full when he chose a card with \(\frac{8}{12}\) on it. He says he will fill his egg carton. Do you agree or disagree? Why? Use a labeled sketch in the egg carton diagram below to help explain your answer.
Answer:
Calvin is correct. He will fill his carton exactly.
Explanation:

Given,
Calvin had \(\frac{1}{3}\) of his egg carton full
when he chose a card with \(\frac{8}{12}\) on it.
\(\frac{1}{3}\) + \(\frac{8}{12}\)
\(\frac{1}{3}\) + \(\frac{2}{3}\)
\(\frac{3}{3}\) = 1
Question 5.
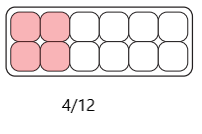
Leah had \(\frac{4}{6}\) of her egg carton full when she chose the \(\frac{5}{12}\) card. Can she fit \(\frac{5}{12}\) in this egg carton? Why or why not? Use a labeled sketch in the egg carton diagram below to help explain your answer.
Answer:
She cannot fit \(\frac{5}{12}\) in the carton because she already has \(\frac{8}{12}\). She can only fit \(\frac{4}{12}\) more.
Explanation:
Question 6.
CHALLENGE Imagine you are playing the game with egg cartons that hold 18 eggs, and the fraction cards refer to 18 eggs instead of 12 eggs. (For example, if you draw the \(\frac{1}{2}\) card, that means half of 18, not half of 12.)
a. If you have \(\frac{2}{3}\) of your first 18-egg carton full, how many more eggs will fit in that carton? What fraction card will you need to draw to fill the first carton exactly?
Answer:
You can fit 6 more eggs. And you need the \(\frac{1}{3}\) card.
Explanation:
Given,
we have \(\frac{2}{3}\) of your first 18-egg carton full
\(\frac{2}{3}\) × 18
= 12
Therefore, You can fit 6 more eggs. And you need the \(\frac{1}{3}\) card.
b. You have \(\frac{1}{3}\) of your second 18-egg carton full when you select the \(\frac{5}{6}\) card. Can you use this card to place more eggs in the second carton, or will you have to use your third carton instead?
Answer:
You can fit \(\frac{2}{3}\) of 18 that is 12 eggs.
And \(\frac{5}{6}\) of 18 is 15 eggs so they will not fit.
Explanation:
Given,
You have \(\frac{1}{3}\) of your second 18-egg carton full
We have selected the \(\frac{5}{6}\) card
\(\frac{5}{6}\) card × 18
15 eggs.
Hence they will not fit.