The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 5 Module 3 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Student Book Answer Key Unit 5 Module 3
Bridges in Mathematics Grade 3 Student Book Unit 5 Module 3 Session 1 Answer Key
More Story Problems
Question 1.
Write your own story problem to fit this equation: 7 × 5 = m
Answer:
Question: A rack has 7 rows haing 5 balloons in each row. How many balloons are in all.
Total number of balloons in the rack (m) = Number of rows in the rack × Number of balloons in each row
= 7 × 5 = 35.
Explanation:
Question: A rack has 7 rows haing 5 balloons in each row. How many balloons are in all.
Answer:
Number of rows in the rack = 7.
Number of balloons in each row = 5.
Total number of balloons in the rack (m) = Number of rows in the rack × Number of balloons in each row
= 7 × 5
= 35.
Question 2.
Write your own story problem to fit this equation: 35 ÷ 5 = n
Answer:
Question: There are 35 ballons in a rack having 5 rows. How many balloons are there in each row.
Total number of balloons in the rack = Number of rows in the rack × Number of balloons in each row
35 ÷ 5 = ??
7 = ??.
Explanation:
Question: There are 35 ballons in a rack having 5 rows. How many balloons are there in each row.
Answer:
Number of balloons in each row = 5.
Total number of balloons in the rack = 35.
Total number of balloons in the rack = Number of rows in the rack × Number of balloons in each row
35 = ?? × 5
35 ÷ 5 = ??
7 = ??.
=> Number of rows in the rack = 7.
Solve each problem in your math journal. Show your thinking using numbers, labeled sketches, or words. Then write an equation that represents the problem and the solution on this page.
Question 3.
Ms. Rowan has 6 tables in her classroom, and 24 students. If she divides the students evenly among the tables, how many students will sit at each table?
Answer:
Number of students will sit at each table = 4.
Explanation:
Number of tables in Ms. Rowan classroom = 6.
Number of students = 24.
Number of students will sit at each table = Number of students ÷ Number of tables in Ms. Rowan classroom
= 24 ÷ 6
= 4.
Question 4.
Teresa has 24 stickers in her sticker book. Each page holds 6 stickers. How many pages does her sticker book have?
Answer:
Number of pages her sticker book have = 4.
Explanation:
Number of stickers in Teresa sticker book = 24.
Number of stickers in each page = 6.
Number of pages her sticker book have = Number of stickers in Teresa sticker book ÷ Number of stickers in each page
= 24 ÷ 6
= 4.
Question 5.
Steve baked 36 cookies. He put 4 cookies in each bag. How many bags of cookies did he have?
Answer:
Number of bags of cookies he have = 9.
Explanation:
Number of cookies Steve baked = 36.
Number of cookies he puts in each bag = 4.
Number of bags of cookies he have = Number of cookies Steve baked ÷ Number of cookies he puts in each bag
= 36 ÷ 4
= 9.
Question 6.
Craig gave his sister 4 boxes of new markers. She was happy to get 36 new markers. How many markers were in each box, if each box held exactly the same number of markers?
Answer:
Number of markers in each box = 9.
Explanation:
Number of boxes of new markers Craig gave his sister = 4.
Total number of new markers she gets = 36.
Number of markers in each box = Total number of new markers she gets ÷ Number of boxes of new markers Craig gave his sister
= 36 ÷ 4
= 9.
Question 7.
Ms. Allyn was getting ready for a math investigation. Each student needed 8 paperclips. She had 32 paperclips. How many students were able to do the investigation?
Answer:
Number of students able to do the investigation = 4.
Explanation:
Number of paperclips each student needed = 8.
Total number of paperclips she had = 32.
Number of students able to do the investigation = Total number of paperclips she had ÷ Number of paperclips each student needed
= 32 ÷ 8
= 4.
Question 8.
The math club was going on a field trip. They were driving 8 school vans. If there were 32 students in the math club, and each van took the same number of students, how many students went in each van?
Answer:
Number of students went in each van = 4.
Explanation:
Number of school vans ther were driving = 8.
Number of students in the math club there were = 32.
Number of students went in each van = Number of students in the math club there were ÷ Number of school vans ther were driving
= 32 ÷ 8
= 4.
Question 9.
Each student in the gym class gathered 4 tennis balls. There were 25 students in the class. Then, the gym teacher divided the balls evenly into 20 different buckets. How many balls are in each bucket?
Which equation would help you solve this problem?
![]() (4 + 25) × 20 = b
(4 + 25) × 20 = b
![]() (4 × 25) + 20 = b
(4 × 25) + 20 = b
![]() (20 ÷ 4) – 24 = b
(20 ÷ 4) – 24 = b
![]() (4 × 25) ÷ 20 = b
(4 × 25) ÷ 20 = b
Answer:
Number of balls are in each bucket = 5.
![]() (4 × 25) ÷ 20 = b.
(4 × 25) ÷ 20 = b.
Explanation:
Number of tennis balls each student in the gym class gathered = 4.
Total number of students in the class = 25.
Then, the gym teacher divided the balls evenly into 20 different buckets.
=> Number of balls evenly the gym teacher divided = 20.
Total number of balls =
Number of balls are in each bucket = ( Number of tennis balls each student in the gym class gathered × Total number of students in the class) ÷ Number of balls evenly the gym teacher divided
= (4 × 25) ÷ 20
= 100 ÷ 20
= 5.
Question 10.
CHALLENGE Mr. Garner gathered $6.50 from each student going to a music festival. He needed to divide the money evenly to pay the field trip helpers: the bus driver, the lunchroom lady, the person running the festival, and the photographer. He has 26 students going to the festival. How much money did he pay each field trip helper?
Answer:
Amount of money he pays each field trip helper = $42.25.
Explanation:
Number of dollars from each student going to a music festival Mr. Garner gathered = $6.50.
Number of students going to the festival = 26.
Number of helpers he needed to divide the money evenly to pay = 4.
Amount of money he pays each field trip helper = (Number of dollars from each student going to a music festival Mr. Garner gathered × Number of students going to the festival) ÷ Number of helpers he needed to divide the money evenly to pay
= ($6.50 × 26) ÷ 4
= $169 ÷ 4
= $42.25.
Division Practice
Question 1.
Fill in the blanks.
3 × __________ = 15
28 ÷ 7 = ____________
__________ × 4 = 24
30 ÷ __________ = 5
3 × 2 = __________
__________ = 8 × 7
399 + 203 = __________
15 ÷ 3 = __________
7 × __________ = 28
24 ÷ __________ = 4
__________ × 5 = 30
__________ ÷ 2 = 3
__________ ÷ 8 = 7
302 – 198 = __________
Answer:
3 × 5 = 15.
28 ÷ 7 = 4.
6 × 4 = 24.
30 ÷ 6 = 5.
3 × 2 = 6.
56 = 8 × 7.
399 + 203 = 602.
15 ÷ 3 = 5.
7 × 4 = 28.
24 ÷ 6 = 4.
6 × 5 = 30.
6 ÷ 2 = 3.
56 ÷ 8 = 7.
302 – 198 = 104.
Explanation:
Given Equations:
3 × ??= 15.
=> ?? = 15 ÷ 3
=> ?? = 5.
28 ÷ 7 = ??
=> 28 ÷ 7 = 4.
?? × 4 = 24.
=> ?? = 24 ÷ 4
=> ?? = 6.
30 ÷ ?? = 5.
=> 30 ÷ 5 = ??
=> 6 = ??.
3 × 2 = ??
=> 3 × 2 = 6.
?? = 8 × 7
=> 8 × 7 = 56.
399 + 203 = ??
=> 399 + 203 = 602.
15 ÷ 3 = ??
=> 15 ÷ 3 = 5.
7 × ?? = 28.
=> ?? = 28 ÷ 7
=> ?? = 4.
24 ÷ ?? = 4.
=> 24 ÷ 4 = ??
=> 6 = ??
?? × 5 = 30.
=> ?? = 30 ÷ 5
=> ?? = 6.
?? ÷ 2 = 3.
=> ?? = 3 × 2
=> ?? = 6.
?? ÷ 8 = 7.
=> ?? = 7 × 8
=> ?? = 56.
302 – 198 = ??
=> 302 – 198 = 104.
Question 2.
Solve the problems below. Show your thinking in words, numbers, or sketches.
a. Mr. See has a collection of stamps. He has 45 total stamps, with 9 stamps on each page. How many pages of stamps does he have?
Answer:
Number of pages of stamps he have = 5.
Explanation:
Total stamps he has = 45.
Number of stamps on each page = 9.
Number of pages of stamps he have = Total stamps he has ÷ Number of stamps on each page
= 45 ÷ 9
= 5.
b. Mrs. Kay has a photo album with 9 pages in it, and 45 photos. How many photos can she put on each page if she wants to put exactly the same number on every page in the album?
Answer:
Number of photos on every page in the album she puts = 5.
Explanation:
Number of pages Mrs. Kay has a photo album = 9.
Total number of photos she has = 45.
Number of photos on every page in the album she puts = Total number of photos she has ÷ Number of pages Mrs. Kay has a photo album
= 45 ÷ 9
= 5.
Bridges in Mathematics Grade 3 Student Book Unit 5 Module 3 Session 2 Answer Key
More Arrays
For the arrays in each pair below:
- Mark the array to show the number you started with (the dividend), the number you divided by (the divisor), and the answer (the quotient).
- Write an equation to represent the problem.
- Fill in the bubble to show whether you were trying to find the number in each group or the number of groups.
Question 1.
Steve baked 36 cookies. He put 4 cookies in each bag. How many bags of cookies did he have?

a. Equation
Answer:
Equation:
Number of bags of cookies he have = 36 ÷ 4 = 9.
Explanation:
Number of cookies Steve baked = 36.
Number of cookies he puts in each bag = 4.
Number of bags of cookies he have = Number of cookies Steve baked ÷ Number of cookies he puts in each bag
= 36 ÷ 4
= 9.
b. The answer to this problem tells
![]() How many in each group
How many in each group
![]() How many groups
How many groups
Answer:
The answer to this problem tells:
![]() How many groups.
How many groups.
Explanation:
Number of cookies Steve baked = 36.
Number of cookies he puts in each bag = 4.
Number of bags of cookies he have = Number of cookies Steve baked ÷ Number of cookies he puts in each bag
= 36 ÷ 4
= 9.
Question 2.
Craig gave his sister 4 boxes of new markers. She was happy to get 36 new markers. How many markers were in each box, if each box held exactly the same number of markers?
a. Equation
Answer:
Equation:
Number of markers in each box = 36 ÷ 4 = 9.
Explanation:
Number of boxes of new markers Craig gave his sister = 4.
Total number of new markers she gets = 36.
Number of markers in each box = Total number of new markers she gets ÷ Number of boxes of new markers Craig gave his sister
= 36 ÷ 4
= 9.
b. The answer to this problem tells
![]() How many in each group
How many in each group
![]() How many groups
How many groups
Answer:
The answer to this problem tells:
![]() How many in each group
How many in each group
Explanation:
Number of boxes of new markers Craig gave his sister = 4.
Total number of new markers she gets = 36.
Number of markers in each box = Total number of new markers she gets ÷ Number of boxes of new markers Craig gave his sister
= 36 ÷ 4
= 9.
Question 3.
Ms. Allyn was getting ready for a math investigation. Each student needed 8 paperclips. She had 32 paperclips. How many students were able to do the investigation?

a. Equation
Answer:
Equation:
Number of students were able to do the investigation = 32 ÷ 8 = 4.
Explanation:
Number of paperclips each student needed = 8.
Total number of paperclips = 32.
Number of students were able to do the investigation = Total number of paperclips ÷ Number of paperclips each student needed
= 32 ÷ 8
= 4.
b. The answer to this problem tells
![]() How many in each group
How many in each group
![]() How many groups
How many groups
Answer:
The answer to this problem tells:
![]() How many groups.
How many groups.
Explanation:
Number of paperclips each student needed = 8.
Total number of paperclips = 32.
Number of students were able to do the investigation = Total number of paperclips ÷ Number of paperclips each student needed
= 32 ÷ 8
= 4.
Question 4.
The math club was going on a field trip. They were driving 8 school vans. If there were 32 students in the math club, and each van took the same number of students, how many students went in each van?

a. Equation
Answer:
Equation:
Number of students went in each van = 32 ÷ 8 = 4.
Explanation:
Number of school vans they were driving = 8.
Number of students in the math club there = 32.
Number of students went in each van = Number of students in the math club there ÷ Number of school vans they were driving
= 32 ÷ 8
= 4.
b. The answer to this problem tells
![]() How many in each group
How many in each group
![]() How many groups
How many groups
Answer:
The answer to this problem tells:
![]() How many in each group.
How many in each group.
Explanation:
Number of school vans they were driving = 8.
Number of students in the math club there = 32.
Number of students went in each van = Number of students in the math club there ÷ Number of school vans they were driving
= 32 ÷ 8
= 4.
Mixed Operations & Story Problems
Question 1.
Fill in the blanks.
6 × __________ = 42
54 ÷ 6 = __________
__________ + 87 = 101
42 ÷ 6 = __________
6 × __________ = 54
101 – 87 = __________
97 – __________ = 55
__________ ÷ 8 = 3
3 × 8 = __________
Answer:
Answer for equations:
6 × 7 = 42.
54 ÷ 6 = 9.
14 + 87 = 101.
42 ÷ 6 = 7.
6 × 9 = 54.
101 – 87 = 14.
97 – 42 = 55.
24 ÷ 8 = 3.
3 × 8 = 24.
Explanation:
6 × ?? = 42.
=> ?? = 42 ÷ 6
=> ?? = 7.
54 ÷ 6 = 9.
?? + 87 = 101.
=> ?? = 101 – 87
=> ?? = 14.
42 ÷ 6 = 7.
6 × ?? = 54.
=> ?? = 54 ÷ 6
=> ?? = 9.
101 – 87 = 14.
97 – ?? = 55.
=> 97 – 55 = ??
=> 42 = ??.
?? ÷ 8 = 3
=> ?? = 3 × 8
=> ?? = 24.
3 × 8 = 24.
Question 2.
Write an equation for each problem. Be sure to include the unit in your final answer. Show your thinking in words, numbers, or sketches. Use your math journal if you need more room.
a. Jeremy is setting up for a party. He has 63 cookies. He puts 7 cookies on each plate. How many plates does he use?
Equation: _______________
Final Answer: _______________
Answer:
Equation: Number of plates he uses = 63 ÷ 7 = 9.
Final Answer: Number of plates he uses = 9.
Explanation:
Number of cookies he has = 63.
Number of cookies on each plate he puts = 7.
Number of plates he uses = Number of cookies he has ÷ Number of cookies on each plate he puts
= 63 ÷ 7
= 9.
b. Katina is helping to set up for the party. She puts 63 brownies on 7 different plates. How many brownies are on each plate?
Equation: _______________
Final Answer: _______________
Answer:
Equation: Number of brownies are on each plate = 63 ÷ 7 = 9.
Final Answer: Number of brownies are on each plate = 9.
Explanation:
Number of brownies she has = 63.
Number of different plates she puts = 7.
Number of brownies are on each plate = Number of brownies she has ÷ Number of different plates she puts
= 63 ÷ 7
= 9.
Question 3.
Write a story problem for each of these equations.
12 × 4 = 48
48 ÷ 4 = 12
Answer:
Problem:
Tim is helping to set up for the party. He puts 4 rows of 12 chairs in each row. How many chairs he has.
Solution: 12 × 4 = 48.
Problem:
Tim is helping to set up for the party. He puts 48 chairs in 4 different rows. How many chairs are in each row.
Solution: 48 ÷ 4 = 12
Explanation:
Tim is helping to set up for the party. He puts 4 rows of 12 chairs in each row. How many chairs he has.
Solution:
Total number of rows he puts the chairs = 4.
Number of chairs in each row = 12.
Total number of chairs he has = Number of chairs in each row × Total number of rows he puts the chairs
= 12 × 4
= 48.
Tim is helping to set up for the party. He puts 48 chairs in 4 different rows. How many chairs are in each row.
Solution:
Total number of chairs = 48.
Number of different rows = 4.
Number of chairs in each row = Total number of chairs ÷ Number of different rows
= 48 ÷ 4
= 12.
Bridges in Mathematics Grade 3 Student Book Unit 5 Module 3 Session 3 Answer Key
Work Place Instructions 5C Line ‘Em Up
Each pair of players needs:
- one 5C Line ‘Em Up Record Sheet
- one 1-6 die and one 4-9 die
- about 100 colored tiles
- 12 red linear pieces
- base ten area and linear pieces (for Game Variation B)
1. Players take turns rolling one die to see who goes first, and then write their names on the record sheet they’re sharing.
2. Player 1 rolls both dice, multiplies the two numbers, and writes an equation on his side of the record sheet to show the product.
3. Player 1 counts out that many tiles and imagines they are bugs or anything else that might be divided into different numbers of lines.
4. Player 1 divides his tiles into 2 lines first. Then he divides them into 3, 4, 5, and 6 lines.
- The player uses red linear pieces each time to show the number of lines he’s making.
- Each time, he records an equation showing the division, making sure his partner is helping and agrees with his equations.
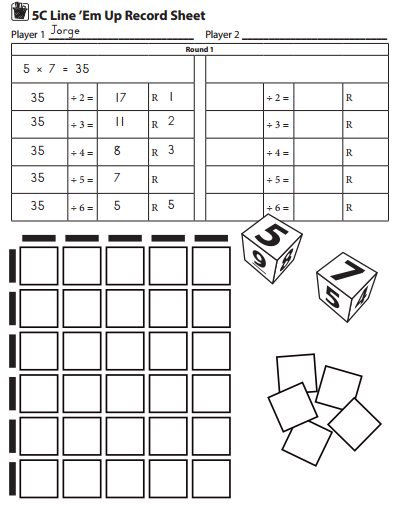
5. Player 2 repeats steps 2-5.
6. After both players have completed two rounds they each add up all their remainders. The player with the higher total wins.
Game Variations
A. Use 2 dice numbered 1-6 instead of 1 die numbered 1-6 and 1 numbered 4-9.
If the product of the roll is 5 or less, players won’t be able to divide it into 6 equal lines, and the amount will be a remainder. For example, if a player rolls 2 × 2 for a product of 4, she won’t be able to divide that amount into 5 or 6 equal lines, and will wind up with the following results:
- 4 ÷ 2 = 2
- 4 ÷ 3 = 1 R1
- 4 ÷ 4 = 1
- 4 ÷ 5 = 0 R4
- 4 ÷ 6 = 0 R4
B. Use 2 dice numbered 4-9 instead of 1 die numbered 1-6 and 1 numbered 4-9.
If players use this game variation, they will need to use base 10 strips and linear pieces instead of the colored tiles and red linear pieces to model and solve at least some of the division combinations.
Connor OK, I rolled an 8 and a 9, and 9 × 8 is 72. Wow—that’s a big number. Maybe I’ll get some big remainders! I’m going to use the base ten pieces for this one—the tiles will take way too long.

Connor 72 divided by 2. It’s 3 strips in each row, and we’ve got 12 left over. That’s going to split into 6 and 6, see?
Rafael Yup, so 72 ÷ 2 is, let’s see, 30 and 6 more for each. It’s 36 with no remainder.
Connor You’re right!

Multiplication Review
Question 1.
Complete the multiplication facts.
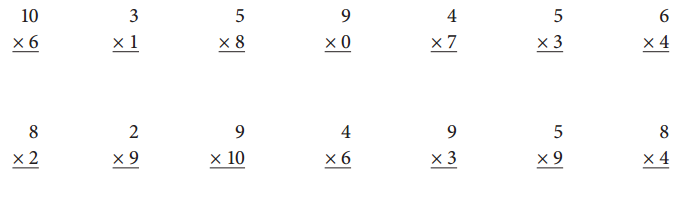
Answer:
The multiplication facts:
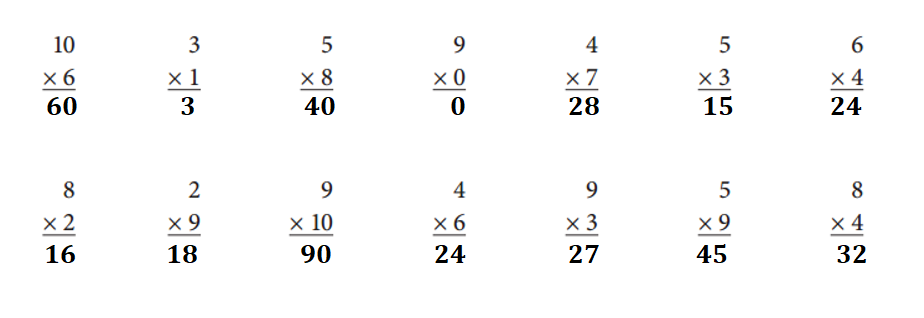
Explanation:
Given Equations:
10 × 6 = 60.
3 × 1 = 3.
5 × 8 = 40.
9 × 0 = 0.
4 × 7 = 28.
5 × 3 = 15.
6 × 4 = 24.
8 × 2 = 16.
2 × 9 = 18.
9 × 10 = 90.
4 × 6 = 24.
9 × 3 = 27.
5 × 9 = 45.
8 × 4 = 32.
Question 2.
Fill in the missing number in each fact. Then write a related division equation.
ex:
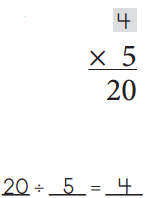
a.
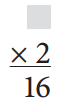
____________ ÷ ___________ = _____________
Answer:
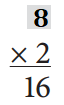
_____16_______ ÷ ______2_____ = ______8_______.
Explanation:
Equation given:
?? × 2 = 16
=> ?? = 16 ÷ 2
=> ?? = 8.
b.
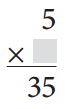
____________ ÷ ___________ = _____________
Answer:
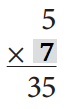
_____35_______ ÷ _____7______ = _______5______.
Explanation:
Equation given:
5 × ?? = 35.
=> ?? = 35 ÷ 5
=> ?? = 7.
c.
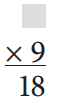
____________ ÷ ___________ = _____________
Answer:
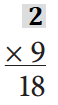
_____18______ ÷ _____9______ = ______2_______.
Explanation:
Equation given:
?? × 9 = 18.
=> ?? = 18 ÷ 9
=> ?? = 2.
Question 3.
CHALLENGE. Use what you know about basic facts to complete these problems.
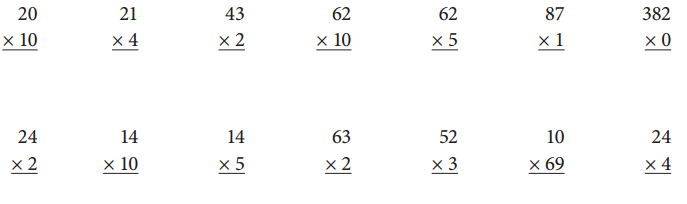
Answer:
The multiplication facts:
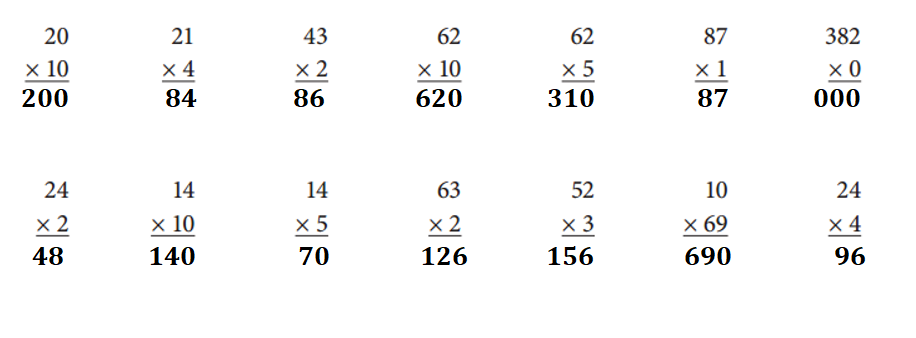
Explanation:
Given equations:
20 × 10 = 200.
21 × 4 = 84.
43 × 2 = 86.
62 × 10 = 620.
62 × 5 = 310.
87 × 1 = 87.
382 × 0 = 0.
24 × 2 = 48.
14 × 10 = 140.
14 × 5 = 70.
63 × 2 = 126.
52 × 3 = 156.
10 × 69 = 690.
24 × 4 = 96.
Bridges in Mathematics Grade 3 Student Book Unit 5 Module 3 Session 4 Answer Key
Work Place Instructions 5D Division Capture
Each pair of players needs:
- 1 5D Division Record Sheet
- 1 clear spinner overlay
- 1 red and 1 blue colored pencil
- the completed Multiplication Table page from their Student Books (optional)
- colored tiles and red linear pieces (optional)
1. Players take turns spinning the spinner. The player who gets the higher number goes first and decides whether he wants to play for red or blue.
2. Player 1 spins the spinner, and uses the number he spins to fill in the answer to one of the division problems on the record sheet, using a pencil in the color he chose.
3. Player 2 takes her turn, and then the players take turns back and forth.
- Each player tries to capture 3 or 4 boxes in a row—across, up and down, or diagonally.
- If the box a player needs is already filled, the player loses that turn and must wait until her next turn to try again.
Note Each number on the spinner has exactly 2 combinations on the grid that match. If a player spins a 3 and there are already two 3s written on the grid, she will not be able to find another and will lose that turn.
4. Players continue to take turns until the record sheet is filled or neither player can use the number he or she spins 3 times in a row.
5. Players each circle the places on the grid where they got 3 or 4 in a row, add up their points, and record their scores on the record sheet.
- Players get 1 point for each row of 3 they capture, and 2 points for each row of 4 they capture.
6. The player with the higher total wins.
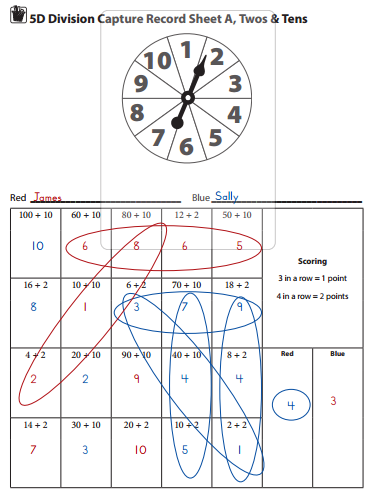
Game Variations
A. Players can use the Multiplication Tables in their Student Books they completed during Unit 2 to help solve the division problems. They can also use the colored tiles and red linear units to help if they want.
B. Players take turns using a regular pencil to fill in the answers to the division problems until the grid is complete. Then they play the game as usual, but they find and circle the answers in their own color pencil instead of writing in the answers as they go.
This makes the game a little easier, because the players just have to search for the numbers they spin, instead of searching for the combinations that will give them those numbers.
C. There are five different Division Capture record sheets, each one a little more challenging than the one before it. Depending on players’ needs, they can:
- Use the same record sheet more than once if they need practice with the facts on that sheet.
- Start with the first record sheet, and use the rest in order over several different Work Place times.
- Start with the record sheet that provides practice with the facts they most need to work on. For example, if both players know their division facts for 2, 3, and 10 pretty well already, they might choose to start with Record Sheet 4 or 5, instead of working through the sheets one by one, starting from 1.
All in the Family
Question 1.
Fill in the missing number in each triangle. Then write the facts in the fact family.
ex:
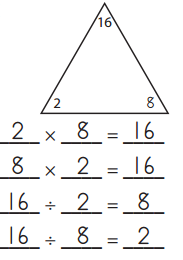
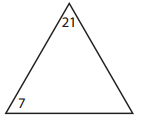
a.
_____________ × _____________ = ______________
_____________ × _____________ = ______________
_____________ ÷ _____________ = ______________
_____________ ÷ _____________ = ______________
Answer:
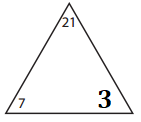
_____7________ × _____3________ = ________21______.
______3_______ × ______7_______ = _________21_____.
____21_________ ÷ ______3_______ = ______7________.
_______21______ ÷ ______7_______ = ______3________.
Explanation:
Missing number in the triangle:
21 ÷ 7 = ??
=> 21 ÷ 7 = 3.
Facts of the family:
7 × 3 = 21.
3 × 7 = 21.
21 ÷ 3 = 7.
21 ÷ 7 = 3.
b.
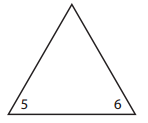
_____________ × _____________ = ______________
_____________ × _____________ = ______________
_____________ ÷ _____________ = ______________
_____________ ÷ _____________ = ______________
Answer:
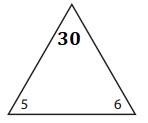
_____5________ × ______6_______ = ______30________.
______6_______ × _______5______ = _______30_______.
____30_________ ÷ _______5______ = ______6________.
____30_________ ÷ _______6______ = ______5________.
Explanation:
Missing number in the triangle:
5 × 6 = ??
=> 5 × 6 = 30.
Facts of the family:
5 × 6 = 30.
6 × 5 = 30.
30 ÷ 6 = 5.
30 ÷ 5 = 6.
c.
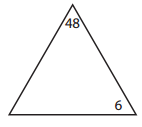
_____________ × _____________ = ______________
_____________ × _____________ = ______________
_____________ ÷ _____________ = ______________
_____________ ÷ _____________ = ______________
Answer:
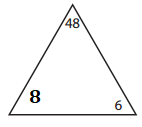
_____6________ × _____8________ = _____48_________.
______8_______ × ______6_______ = ______48________.
_____48________ ÷ _____8________ = ______6________.
_____48________ ÷ ______6_______ = _______8_______.
Explanation:
Missing number in the triangle:
48 ÷ 6 = ??
=> 48 ÷ 6 = 8.
Facts of the family:
6 × 8 = 48.
8 × 6 = 48.
48 ÷ 6 = 8.
48 ÷ 8 = 6.
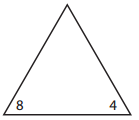
d.
_____________ × _____________ = ______________
_____________ × _____________ = ______________
_____________ ÷ _____________ = ______________
_____________ ÷ _____________ = ______________
Answer:
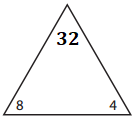
______4_______ × _____8________ = _______32_______.
______8_______ × ______4_______ = ______32________.
_____32________ ÷ ______8_______ = ______4________.
______32_______ ÷ ______4_______ = ______8________.
Explanation:
Missing number in the triangle:
8 × 4 = ??
=> 8 × 4 = 32.
Facts of the family:
8 × 4 = 32.
4 × 8 = 32.
32 ÷ 4 = 8.
32 ÷ 8 = 4.
e.
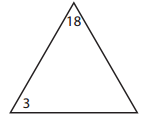
_____________ × _____________ = ______________
_____________ × _____________ = ______________
_____________ ÷ _____________ = ______________
_____________ ÷ _____________ = ______________
Answer:
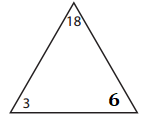
_____3________ × _____6________ = ______18________.
_____6________ × ______3_______ = _____18_________.
_____18________ ÷ ______6_______ = ______3________.
_____18________ ÷ _______3______ = _____6_________.
Explanation:
Missing number in the triangle:
18 ÷ 3 = ??
=> 18 ÷ 3 = 6.
Facts of the family:
3 × 6 = 18.
6 × 3 = 18.
18 ÷ 3 = 6.
18 ÷ 6 = 3.
Question 2.
CHALLENGE Use multiplication and division to find the secret path through each maze. You can only move one space up, down, over, or diagonally each time. Write two equations to explain the path through the maze.
ex:
a.
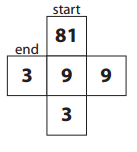
Answer:
Explanation:
Equations:
Start: 9 × 9 = 81.
End: 3 × 3 = 9.
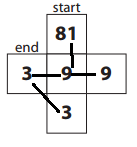
b.
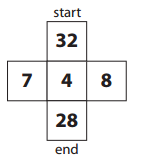
Answer:
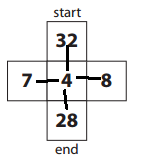
Explanation:
Equations:
Start: 8 × 4 = 32.
End: 7 × 4 = 28.