The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 1 Module 2 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Student Book Answer Key Unit 1 Module 2
Bridges in Mathematics Grade 3 Student Book Unit 1 Module 2 Session 1 Answer Key
Subtraction Fact Practice
Question 1.
Solve these zero facts.
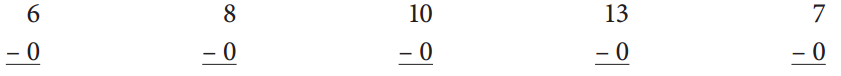
Answer:
Subtract the given zeros from the respective numbers which are 6 , 8, 10 , 13 and 7 and get the result as shown below.
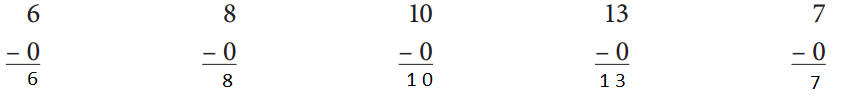
Question 2.
Solve these Count Back facts.
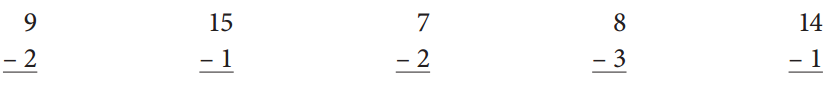
Answer:
Subtract the given numbers 2, 1, 2 , 3 and 1 from the respective numbers which are 9, 15, 7, 8 and 14 and get the result as shown below.
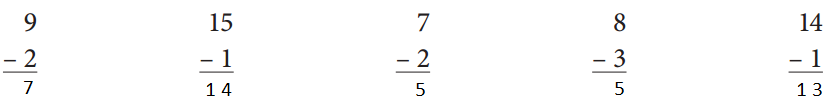
Question 3.
Solve these Take All facts.
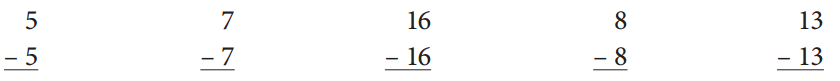
Answer:
Subtract the given numbers 5, 7, 16, 8, 13 from the respective numbers which are 5, 7, 16, 8, 13 and get the result as shown below.
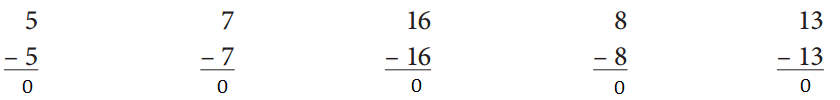
Question 4.
Solve these Neighbors facts.
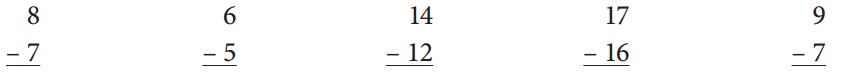
Answer:
Subtract the given numbers 7, 5, 12, 16, 7 from the respective numbers which are 8, 6, 14, 17, 7 and get the result as shown below.
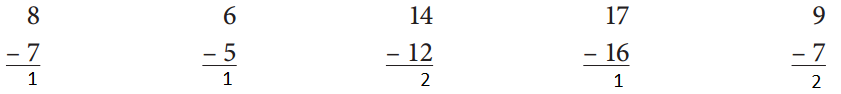
Question 5.
Jessica has 16 marbles. Nine marbles roll under her bed. How many marbles does Jessica still have in front of her? Show all your work using numbers, words, or labeled sketches.
Answer:
Number of marbles Jessica having = 13
Number of marbles rolled under her bed = 9
Number of marbles contain in front of her = ?
= 13 – 9
= 4
Therefore 4 marbles are present in front of her.
Bridges in Mathematics Grade 3 Student Book Unit 1 Module 2 Session 2 Answer Key
Each pair of players needs:
- 1 deck of Number Cards to share, with wild cards removed
- 2 Target Twenty Record Sheets (1 per player) and a pencil
1. One player shuffles the cards and places the deck face-down. Each player takes 5 cards.
2. Each player chooses the 3 cards in their hand that have a sum as close to 20 as possible.
3. Each player writes an equation on their record sheet showing the 3 numbers and their sum.
4. Players check each other’s work, compute their scores (the difference between 20 and their sum), and record both scores on their record sheets.

5. Players put the cards they used face-up in a discard pile. Then each player takes 3 new cards from the deck so they have 5 cards again.
6. The game continues for a total of 5 rounds.
7. At the end of the game, players add their own scores. The player with the lower score wins.
Game Variations
A. Players return the wild cards to the deck. If a player gets a wild card, they can decide to make it any number between 0 and 10. If a player uses a wild card, they mark a star above the number assigned to the wild card in the equation on their record sheet.
B. Players can use 30, 40, or 50 as their target number. They will need to use 4, 5, or 6 cards to make these larger numbers.
More Subtraction Fact Practice
Question 1.
Solve the Take Away Ten facts below.
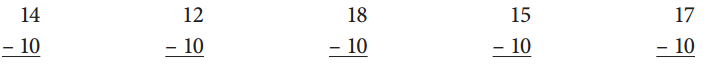
Answer:
Subtract the given tens from the respective numbers which are 14, 12, 18, 15 and 17 and get the result as shown below.
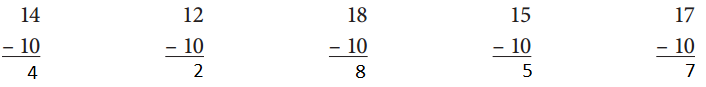
Question 2.
Solve the Take Half facts below.
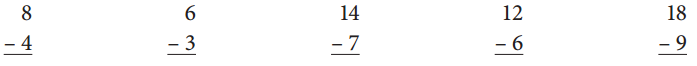
Answer:
Subtract the given numbers 4, 3 , 7 , 6 and 9 from the respective numbers which are 8 , 6, 14 , 12 and 18 and get the result as shown below.
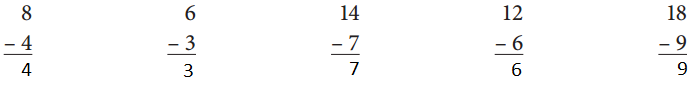
Question 3.
Solve the Leftover facts below.
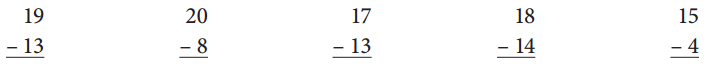
Answer:
Subtract the given numbers 13, 8, 13 , 14 and 4 from the respective numbers which are 19, 20 , 17 , 18 and 15 and get the result as shown below.
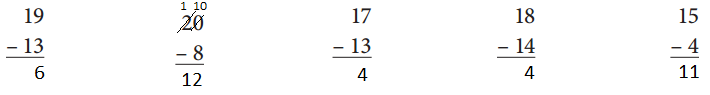
Question 4.
Clarence is 42 inches tall. His brother Charlie is 37 inches tall. How much taller is Clarence? Show all your work using numbers, words, or labeled sketches.
Answer:
Actual Height of Clarence = 42
Height of Charlie = 37
Height of Clarence than his brother Charlie= ?
= 42 – 37
= 5
Therefore Clarence is 5 inches taller than his brother Charlie.
Question 5.
Complete each equation by writing a different pair of numbers with a difference of 9.
a. ___ – ___ = 9
Answer:
The Equation when 3 is subtracted from 12 generates the value 9 as shown below.
12 – 3 = 9
b. ___ – ____ = 9
Answer:
The Equation when 9 is subtracted from 18 generates the value 9 as shown below.
18 – 9 = 9
c. ___ – ____ = 9
Answer:
The Equation when 11 is subtracted from 20 generates the value 9 as shown below.
20 – 11 = 9
Bridges in Mathematics Grade 3 Student Book Unit 1 Module 2 Session 3 Answer Key
Work Place Instructions 1C Blast Off to Space
Each pair of players needs:
- 1 clear spinner overlay (players share)
- Blast Off to Space Game Board (1 per player)
- IC Blast Off to Space Record Sheet (1 per player)
- game markers (8 per player)
- pencil (1 per player)
1. Each player places eight rockets (markers) on the launch pads of their choice on their game boards. Players can put more than one rocket on a pad.
2. Player 1 spins each spinner once to create a subtraction equation and solves the problem. Player 1 shows how she solved the problem, explaining the strategies she used.
3. Then, Player 1 records the equation on her record sheet.
4. If there is a rocket on the difference, that rocket can blast off to space!
5. Whether or not a rocket blasts off, it is now Player 2’s turn. Player 2 repeats steps 3-5.
6. Players take turns until one player has launched four rockets.
7. Then, players reposition their rockets. Players can use their record sheets to help them think about which numbers might occur more often than others.
Jayden It looks like we’ve been getting a lot of 8s and 9s Thomas We’ve hardly gotten any 3s or 13s.
Jayden I’m going to move my markers to 8 and 9.
Thomas Me too. I’m going to put one on 7 too.
8. The game is over when all of one player’s rockets have been blasted into space.
Game Variations
A. Players can use more game markers (10 per person) or fewer (6 per person).
B. Players add 5 or 10 to each number they spin.
More Games Story Problems
Question 1.
Asha and Oliver are playing Blast Off to Space. In this game, players spin two numbers, find the number that is the difference between the numbers, and ‘blast off’ a rocket with that number.
ex Asha spun a 16 and a 9. What rocket could she blast off for 16 and 9?
Asha can blast off rocket 7, because 16 – 9 = ![]()
a. Oliver spun a 14 and an 8. What rocket could he blast off for 14 and 8?
Answer:
Given Oliver spun a 14 and an 8
Oliver can blast off the rocket 6 , since 14 – 8 = 6.
b. Asha has a rocket on a 7. What are two numbers she could spin to be able to blast off her rocket on 7?
Answer:
Given Asha a rocket of 7
14 and 8 are two numbers she can spin in order to blast off her rocket on the 7
Question 2.
Raven and Todd are playing a game with marbles. There are 20 marbles in all. The player with the most marbles at the end of the game wins.
a. After one game, Raven has 13 marbles. How many marbles does Todd have? Show all your work using numbers, words, or labeled sketches.
Answer:
Total Number of marbles = 20
Number of marbles Raven has = 13
Number of Marbles Todd have = ?
= 20 – 13
= 7
Therefore Todd have 7 marbles.
b. After another game, Todd has 9 marbles. How many marbles does Raven have? Show all your work using numbers, words, or labeled sketches.
Answer:
Total Number of marbles = 20
Number of marbles Todd has = 9
Number of Marbles Raven have = ?
= 20 – 9
= 11
Therefore Raven have 7 marbles.
Question 3.
CHALLENGE James and Lily are playing basketball. Lily has 57 points. James has 38 points. How many more points does Lily have? Record your work in your math journal, using numbers, words, or labeled sketches. Record the answer here.
Answer:
Number of points Lilly Contain = 57
Number of points James Contain = 38
Number of more points Lilly have than James = ?
= 57 – 38
= 19
Therefore Lilly contain 19 points than James.
Bridges in Mathematics Grade 3 Student Book Unit 1 Module 2 Session 4 Answer Key
Addition & Subtraction Equations
Question 1.
Complete the following equations.
12 = 4 + 8 8 + ___ = 15 ___ + 7 = 13
3 = 13 – 10 14 – = 9 ___ – 8 = 8
8 + ___ = 14 5 = 17 – ___ 10 = 18 – ___
Answer:
12 = 4 + 8 8 + 7 = 15 6 + 7 = 13
3 = 13 – 10 14 – 5 = 9 16 – 8 = 8
8 + 6 = 14 5 = 17 – 12 10 = 18 – 8
Question 2.
Choose one of the equations above and explain how you figured out the missing number using words, numbers, models, or pictures.
Answer:
12 = 4 + 8 8 + ___ = 15 ___ + 7 = 13
The answer for the given Equation is 12 = 4 + 8 8 + 7 = 15 6 + 7 = 13 .When 8 is subtracted from 15 the value obtained is 7. So 7 is placed in the given first missing blank. Similarly When 7 is subtracted from 13 the value obtained is 6. So 6 is placed in the given second missing blank.
Question 3.
Complete the following equations.
3 + 7 = ____ + 6 9 + 6 = 10 + ____
5 + ___ = 10 + 2 ____ + 8 = 1 + 10
Answer:
1). Add the given numbers 3 and 7 and get the result as 10 and place the value 10 in first missing blank for the first Given Equation.
Then Add both 9 and 6 which gives the value as 15 , after that subtract the given value 10 from 15 which gives the value as 5 .Then place 5 in second missing blank given.
2).The second Equation is also follows the same procedure.
3 + 7 = 4 + 6 9 + 6 = 10 + 5
5 + 5 = 10 + 2 + 3 + 8 = 1 + 10
Work Place Instructions 1D Subtraction Bingo
Each pair of players needs:
- 2 Subtraction Bingo Record Sheets
- 2 colored pencils
- 1 deck of Number Cards
1. Each player chooses a separate board, either Board A or Board B. One player shuffles the cards and places the deck face-down. Each player takes 5 cards.
2. Player A chooses 2 cards to add and finds the sum. Then Player A chooses a third card to subtract from the sum. Player A records the subtraction problem under the bingo board.
For example, Player A chooses a 7 and a 9 to add: 7 + 9 = 16. Then, Player A chooses an 8 to subtract from the sum, and solves and records the problem 16 – 8 = 8.
3. Then, Player A looks for a problem on the bingo board that is equivalent to the subtraction problem he just made. If there is an equivalent problem, Player A explains her thinking to Player B. If Player B agrees, Player A puts an X over the equivalent problem on the game board.
If Player B disagrees with any of Player A’s thinking, Player A has to rethink her work until she proves it to Player B. Trina Hmmm, I got 15 – 8. That’s 7.1 don’t see 15 – 8 on the board anywhere.
Audrey That’s OK. Do you see anything that equals 15 – 8?
Trina I don’t see 7 on the board anywhere.
Audrey I know, but do you see anything that equals 7? Like 12 – 5? That equals 7.
Trina Oh, I get it. OK, I see 13 – 6. That equals 7. Is that what I cross off?
Audrey Yes!
4. Player B repeats steps 3 and 4.
5. Players continue until one player crosses out 4 problems in a row. They can be vertical, horizontal, or diagonal. Whoever gets 4 in a row first wins the game.
Game Variations
A. Players use 3 cards instead of 5 to make the game simpler and less strategic, so they focus on addition and subtraction strategies.
B. Players continue until one player gets 3 in a row. Or they play until the entire board is crossed out.
C. Players make problems with all 5 cards. First they add 3 cards together. Then they add the other 2
cards together and subtract this sum from the sum of the first 3 cards.
D. Players play on the same board, using two different colored pencils. Players try to get 3 problems in a row. In this version, players are also thinking about blocking their partner from getting 3 in a row.
Addition & Subtraction Mixed Review
Question 1.
Find each sum.
24 + 10 = ____ 34 + 10 = _____ 24 + 30 = _____
27 + 30 = _______ 34 + 20 = _____
Answer:
Add both the given Respective numbers then, get the result and place them in the given missing blanks as shown below.
24 + 10 = 34 34 + 10 = 44 24 + 30 = 54
27 + 30 = 57 34 + 20 = 54
Question 2.
Find each difference.
37 – 10 = ______ 37 – 20 = ______ 37 – 21 = _____
37 – 22 = ________ 37 – 25 = _____
Answer:
Subtract both the given Respective numbers then ,get the result and place them in the given missing blanks as shown below.
37 – 10 = 27 37 – 20 = 17 37 – 21 = 16
37 – 22 = 15 37 – 25 = 12
Question 3.
Complete each equation with a different pair of numbers whose sum is 13.
a. ____ + ____ = 13
Answer:
The Equation when 7 and 6 are added generates the value 13 as shown below
7 + 6 = 13
b. ____ + ____ = 13
Answer:
The Equation when 10 and 3 are added generates the value 13 as shown below
10 + 3 = 13
c. ____ + ____ = 13
Answer:
The Equation when 9 and 4 are added generates the value 13 as shown below
9 + 4 = 13
Question 4.
Write an equation that could represent this picture.
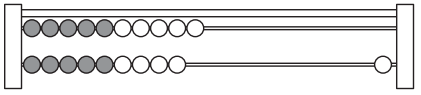
Answer:
The Equation that could represent this picture = 9 + 10 = 19