The solutions to Bridges in Mathematics Grade 3 Home Connections Answer Key Unit 3 Module 4 can help students to clear their doubts quickly.
Bridges in Mathematics Grade 3 Home Connections Answer Key Unit 3 Module 4
Bridges in Mathematics Grade 3 Home Connections Unit 3 Module 4 Session 2 Answer Key
Which Strategy?
Note to Families
At school, we have been exploring the standard (or traditional) algorithm for addition. Another name for this strategy is the regrouping method. We’ve compared the standard algorithm to other strategies we have learned this year. Ask your child questions about the strategies he or she is using.
Question 1.
Use the standard algorithm to solve each problem. Then solve it a different way. Label your method. Circle the strategy that seemed quicker and easier.
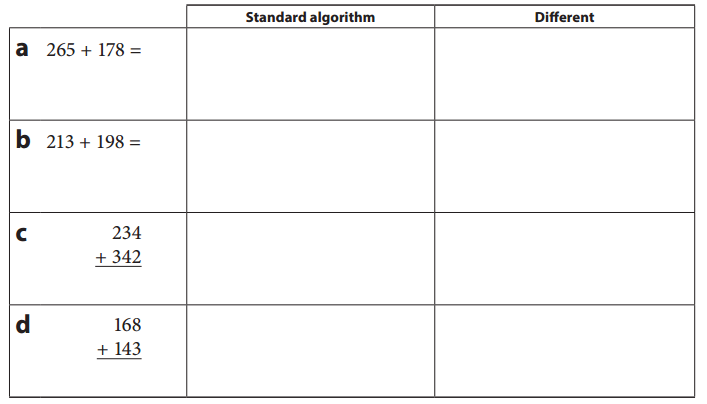
Answer:
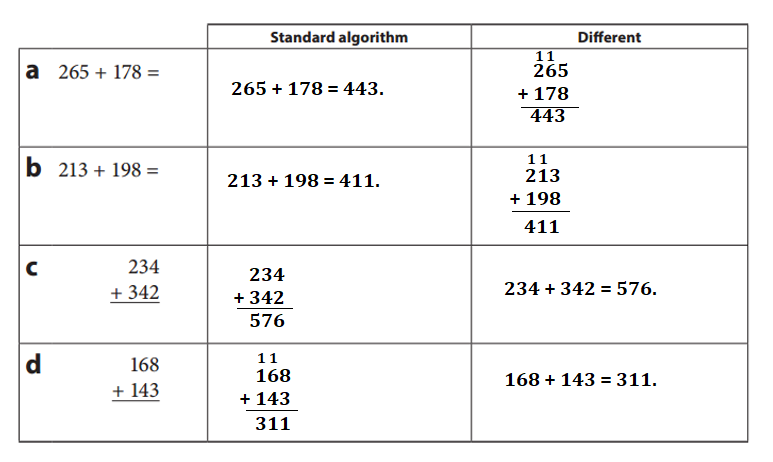
Explanation:
Standard algorithm Different
a. 265 + 178 = 443. Add from Right to left. Place value.
Given Equations: Standard algorithm Different
a. 265 + 178 = 443. 443.
b. 213 + 198 = 411. 411.
c. 234 + 342 = 576. 576.
d. 168 + 143 = 311. 311.
Question 2.
Conrad is making bread. After he mixes the ingredients together, he has to let the bread rise for 95 minutes. Then, the bread will bake for 58 minutes.
a. How long will it take for the bread to rise and bake? Show your thinking using numbers, sketches, or words.
Answer:
Number of minutes it takes for the bread to rise and bake = 153.
Explanation:
Number of minutes he has to let the bread rise = 95.
Number of minutes the bread will bake = 58.
Number of minutes it takes for the bread to rise and bake = Number of minutes he has to let the bread rise + Number of minutes the bread will bake
= 95 + 58
= 153.
b. What strategy did you use to solve this problem? Why?
Answer:
The strategy I used to solve this problem is addition from right to left adding numbers.
Explanation:
Number of minutes he has to let the bread rise = 95.
Number of minutes the bread will bake = 58.
Number of minutes it takes for the bread to rise and bake = Number of minutes he has to let the bread rise + Number of minutes the bread will bake
= 95 + 58
= 153.
Question 3.
Saima is training for a bike race. On Saturday, she rode her bike for 172 minutes. On Sunday, she rode for 153 minutes.
a. How much longer did she ride her bike for on Saturday than on Sunday? Show your thinking using numbers, sketches, or words.
Answer:
Number of minutes she rides her bike for on Saturday than on Sunday = 19.
Explanation:
Number of minutes On Saturday, she rode her bike = 172.
Number of minutes On Sunday, she rode her bike = 153.
Difference:
Number of minutes she rides her bike for on Saturday than on Sunday = Number of minutes On Saturday, she rode her bike – Number of minutes On Sunday, she rode her bike
= 172 – 153
= 19.
b. What strategy did you use to solve this problem? Why?
Answer:
The strategy I used to solve this problem is subtraction method, subtracting from right to left/
Explanation:
Number of minutes On Saturday, she rode her bike = 172.
Number of minutes On Sunday, she rode her bike = 153.
Difference:
Number of minutes she rides her bike for on Saturday than on Sunday = Number of minutes On Saturday, she rode her bike – Number of minutes On Sunday, she rode her bike
= 172 – 153
= 19.
c. CHALLENGE Before she rides her bike, Saima warms up for 12 minutes. On Tuesday, Saima rode her bike for 52 miles. If it takes Saima 6 minutes to ride each mile, how long did it take for Saima to warm up and ride her bike on Tuesday?

Answer:
Number of minutes it takes for Saima to warm up and ride her bike on Tuesday = 324.
Explanation:
Number of minutes Saima warms up = 12.
Number of miles she rode her bike on Tuesday = 52.
Number of minutes to ride each mile she takes = 6.
Total number of minutes to ride she takes = Number of miles she rode her bike on Tuesday × Number of minutes to ride each mile she takes
= 52 × 6
= 312.
Number of minutes it takes for Saima to warm up and ride her bike on Tuesday = Number of minutes Saima warms up + Total number of minutes to ride she takes
= 12 + 312
= 324.
Combinations of 1,000
Question 4.
Fill in the missing numbers to make a total of 1,000 in each box.
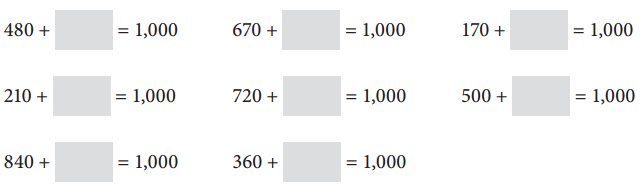
Answer:
Addition:
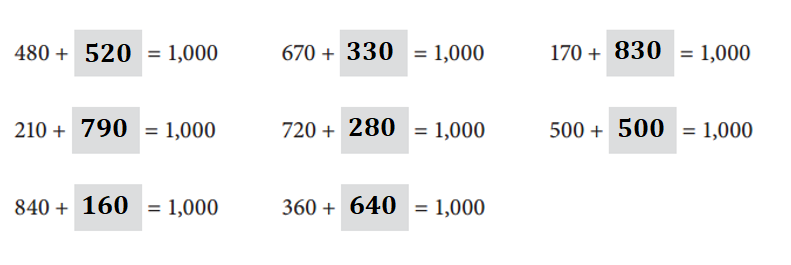
Explanation:
Given Equations:
480 + ??? = 1,000.
=> ??? = 1,000 – 480.
=> ??? = 520.
670 + ??? = 1,000.
=> ??? = 1,000 – 670.
=> ??? = 330.
170 + ??? = 1,000.
=> ??? = 1,000 – 170.
=> ??? = 830.
210 + ??? = 1,000.
=> ??? = 1,000 – 210.
=> ??? = 790.
720 + ??? = 1,000.
=> ??? = 1,000 – 720.
=> ??? = 280.
500 + ??? = 1,000.
=> ??? = 1,000 – 500.
=> ??? = 500.
840 + ??? = 1,000.
=> ??? = 1,000 – 840.
=> ??? = 160.
360 + ??? = 1,000.
=> ??? = 1,000 – 360.
=> ??? = 640.
Bridges in Mathematics Grade 3 Home Connections Unit 3 Module 4 Session 4 Answer Key
Estimates, Sums & Story Problems
Question 1.
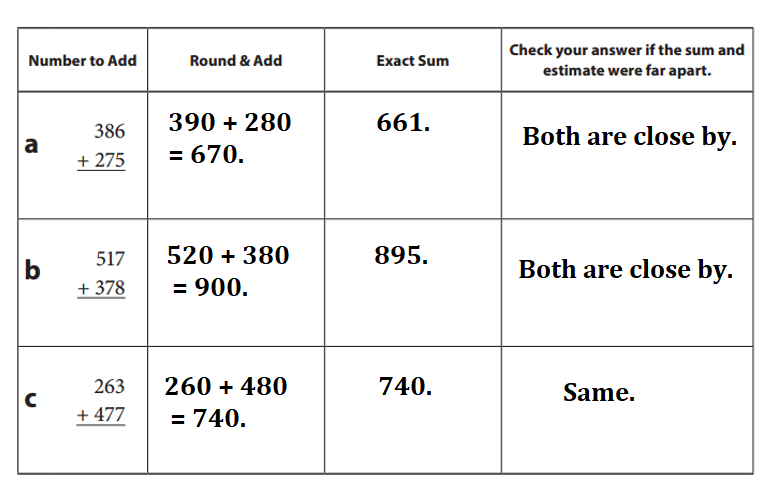
Round each pair of numbers to the nearest ten, and then add the rounded numbers to estimate the sum. Then use any strategy you like to find the exact sum. Compare the exact sum to your estimate to make sure that it makes sense. If your answer does not make sense, double-check your work or solve the problem another way.
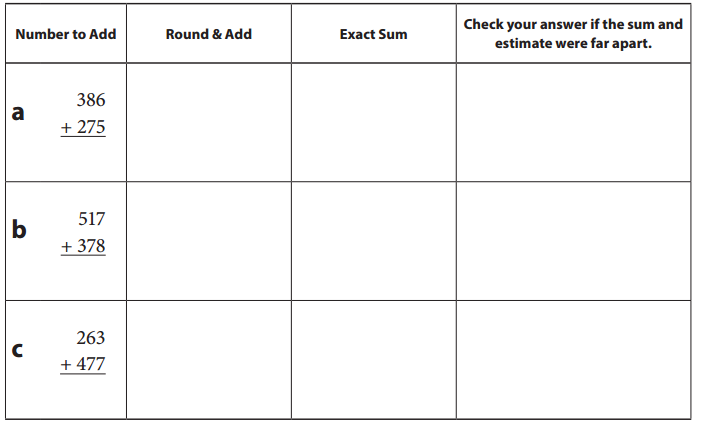
Answer:
Addition:
Explanation:
Given Equations: Round & Add Exact Sum Check
a. 386 + 275 = 390 + 280 = 670. 661. Both are close by.
b. 517 + 378 = 520 + 380 = 900. 895. Both are close by.
c. 263 + 477 = 260 + 480 = 740. 740. Same.
Question 2.
Use estimation to answer each question yes or no. Do not find exact sums.
a. Shawna has a photo album with space for 160 pictures. She has 33 pictures of her family, 48 pictures from summer camp, and 57 pictures from school. Does she have enough pictures to fill the photo album?
Answer:
Yes, she has enough pictures to fill the photo album because she has less than 160 total pictures.
Explanation:
Number of pictures Shawna has a photo album with space = 160.
Number of pictures She has of her family = 33.
Number of pictures she has from summer camp = 48.
Number of pictures she has from school = 57.
Total number of pictures she has = Number of pictures She has of her family + Number of pictures she has from summer camp + Number of pictures she has from school
= 33 + 48 + 57
= 81 + 57
= 138.
b. Fred needs 410 game markers to play a game with his classmates and their families on Family Math Night. He has 96 red markers, 123 blue markers, 106 yellow markers, and 72 green markers. Does he have enough game markers to play the game?
Answer:
No, he doesnot has enough markers to play game.
Explanation:
Number of game markers to play a game Fred needs = 410.
Number of red markers he has = 96.
Number of blue markers he has = 123.
Number of yellow markers he has = 106.
Number of green markers he has = 72.
Total number of markers he has = Number of red markers he has + Number of blue markers he has + Number of yellow markers he has + Number of green markers he has
= 96 + 123 + 106 + 72
= 219 + 106 + 72
= 325 + 72
= 397.
Question 3.
Jasmine’s neighbor paid her $32 for helping with some yard work. Jasmine gave her brother $8 because he helped her with some of the work. Then she went shopping with the rest of the money. She bought 3 books that were $6 each and a bottle of juice for $1.89. How much money did she have left? Show all your work.
Answer:
Amount of money left with her = $ 4.11.
Explanation:
Amount of money Jasmine’s neighbor paid her for helping with some yard work = $32.
Amount of money Jasmine gave her brother = $8.
Cost of 3 books bought = $6 each = $6 × 3 = $18.
Cost of a bottle of juice = $1.89.
Amount of money left with her = Amount of money Jasmine’s neighbor paid her for helping with some yard work – (Amount of money Jasmine gave her brother + Cost of 3 books bought + Cost of a bottle of juice)
= $32 – ($8 + $18 + $1.89)
= $32 – ($26 + $1.89)
= $32 – $27.89
= $ 4.11.
Question 4.
The third graders are putting on a play for the fourth and fifth graders. They need to set up chairs in the gym for the fourth and fifth graders to sit on. There are 86 fourth graders, 79 fifth graders, 3 fourth grade teachers, and 3 fifth grade teachers. How many chairs will the third graders need to set up? Show all your work.
Answer:
Number of chairs the third graders need to set up = 171.
Explanation:
Number of students of fourth graders = 86.
Number of students of fifth graders = 79.
Number of fourth grade teachers = 3.
Number of fifth grade teachers = 3.
Number of chairs the third graders need to set up = Number of students of fourth graders + Number of students of fifth graders + Number of fourth grade teachers + Number of fifth grade teachers)
= 86 + 79 + 3 + 3
= 165 + 3 + 3
= 168 + 3
= 171.
Question 5.
CHALLENGE The third graders can put no more than 20 chairs in a row. How many rows of chairs will they need? Show all your work.
Answer:
Number of rows of chairs will they need = 9.
Explanation:
Number of students of fifth graders = 79.
Number of fourth grade teachers = 3.
Number of fifth grade teachers = 3.
Number of chairs the third graders need to set up = Number of students of fourth graders + Number of students of fifth graders + Number of fourth grade teachers + Number of fifth grade teachers)
= 86 + 79 + 3 + 3
= 165 + 3 + 3
= 168 + 3
= 171.
Number of chairs in a row the third graders can put = 20.
Number of rows of chairs will they need = Number of chairs the third graders need to set up ÷ Number of chairs in a row the third graders can put
= 171 ÷ 20
= 8 quotient 11 remainder.
= 9.