Practicing the Bridges in Mathematics Grade 2 Student Book Answer Key Unit 5 Place Value to One Thousand will help students analyze their knowledge of concepts.
Bridges in Mathematics Grade 2 Student Book Answer Key Unit 5 Place Value to One Thousand
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 1 Session 2 Answer Key
Pick-Up Sticks Record Sheet
Question 1.
Estimate how many sticks are in the container at your table.
I think there are _____________ sticks in the container.
Answer:
I think there are 529 sticks in the container.
Explanation:
Estimation:
Number of sticks are in the container at our table = 500 to 600.
Actually,
Number of sticks are in the container at our table = 529.
Question 2.
How many sticks did each group actually count? Record the numbers on the lines below.
Answer:
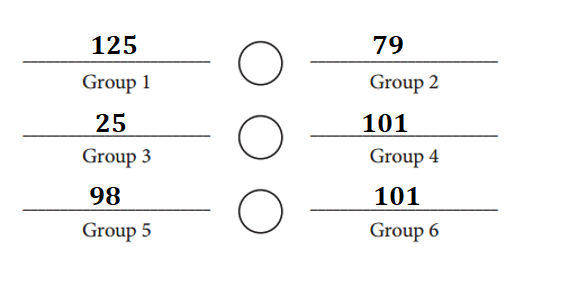
Explanation:
Group 1: Counted – 125 sticks.
Group 2: Counted – 79 sticks.
Group 3: Counted – 25 sticks.
Group 4: Counted – 101 sticks.
Group 5: Counted – 98 sticks.
Group 6: Counted – 101 sticks.
Question 3.
Write a greater than >, less than <, or equal sign = in each of the circles above to compare the numbers.
Answer:
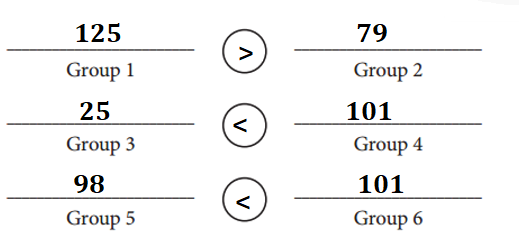
Explanation:
Group 1: Counted – 125 sticks is greater than Group 2: Counted – 79 sticks.
Group 3: Counted – 25 sticks is lesser than Group 4: Counted – 101 sticks.
Group 5: Counted – 98 sticks is lesser than Group 6: Counted – 101 sticks.
Question 4.
Write the numbers of sticks in order from least to greatest on the lines below.
Answer:
The numbers of sticks in order from least to greatest on the lines below:
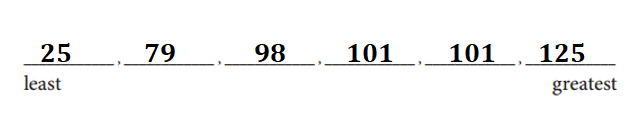
Explanation:
Group 3: Counted – 25 sticks.
Group 2: Counted – 79 sticks.
Group 5: Counted – 98 sticks.
Group 4: Counted – 101 sticks.
Group 6: Counted – 101 sticks.
Group 1: Counted – 125 sticks.
Question 5.
How many sticks are there in all?
Answer:
Total number of sticks are there in all = 529.
Explanation:
Group 1: Counted – 125 sticks.
Group 2: Counted – 79 sticks.
Group 3: Counted – 25 sticks.
Group 4: Counted – 101 sticks.
Group 5: Counted – 98 sticks.
Group 6: Counted – 101 sticks.
Total number of sticks = Group 1 + Group 2 + Group 3 + Group 4 + Group 5 + Group 6
= 125 + 79 + 25 + 101 + 98 + 101
= 204 + 25 + 101 + 98 + 101
= 229 + 101 + 98 + 101
= 330 + 98 + 101
= 428 + 101
= 529.
Question 6.
Write the total on each of the lines below. Then write a greater than >, less than < or equal sign = in each circle to compare the numbers.

Answer:

Explanation:
Total number of sticks are there in all = 529.
=> 529 is lesser than 750.
=> 529 is lesser than 999.
=> 529 is lesser than 1,040.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 1 Session 3 Answer Key
Counting Cubes Record Sheet
Question 1.
Estimate how many cubes are in the container at your table.
I think there are _____________ cubes in the container.
Answer:
I think there are 501 cubes in the container.
Explanation:
Estimation of cubes on my table:
Number of cubes are in the container at my table = 425.
There are 501 cubes in the container.
Question 2.
How many cubes were there in your container? Write the answer in four different ways below.
a. Number ________________
Answer:
Number of cubes in my container = 501.
Explanation:
Number of cubes are there in my container = 501.
b. Words ________________
Answer:
Five Hundred and one cubes are there in my container.
Explanation:
Number of cubes are there in my container = 501.
c. Hundreds, Tens and Ones ________________
Answer:
5 Hundreds 0 Tens and 1 Ones cubes are there in my container.
Explanation:
Number of cubes are there in my container = 501.
=> 5 Hundreds 0 Tens and 1 Ones.
d. Expanded notation ________________
Answer:
Expanded Form: 5(100) + 0(10) + 1(1) = 501 cubes are there in my container.
Explanation:
Number of cubes are there in my container = 501.
Expanded Form: 5(100) + 0(10) + 1(1)
= 500 + 0 + 1
= 500 + 1
= 501.
Thinking About 1,000
Question 3.
999 + 1 and 500 + 500 are two different ways to make 1,000. Write some other ways to make 1,000 in the space below. You can use addition or subtraction; even multiplication if you like. You can also use more than two addends.
Answer:
Some other ways to make 1,000:
600 + 400 = 1,000.
300 + 500 + 200 = 1,000.
900 + 100 = 1,000.
200 + 200 + 600 = 1,000.
Explanation:
999 + 1 and 500 + 500 are two different ways to make 1,000.
Some other ways to make 1,000:
600 + 400 = 1,000.
300 + 500 + 200
= 800 + 200
= 1,000.
900 + 100 = 1,000.
200 + 200 + 600
= 400 + 600
= 1,000.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 1 Session 4 Answer Key
Place Value Triple Roll Record Sheet



Put the 6 scores in order from least to greatest.
Answer:



Numbers from least to greatest:
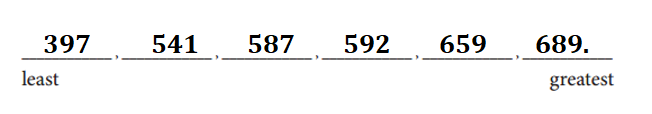
Explanation:
Round 1: 100s 10s 1s Total
Blue team = 5 4 1 = 541.
Red team = 3 9 7 = 397.
=> 541 is greater than 397.
Round 2: 100s 10s 1s Total
Blue team = 6 8 9 = 689.
Red team = 5 9 2 = 592.
=> 689 is greater than 592.
Round 3: 100s 10s 1s Total
Blue team = 6 5 9 = 659.
Red team = 5 8 7 = 587.
=> 659 is greater than 587.
6 scores in order from least to greatest
397, 541, 587, 592, 659, 689.
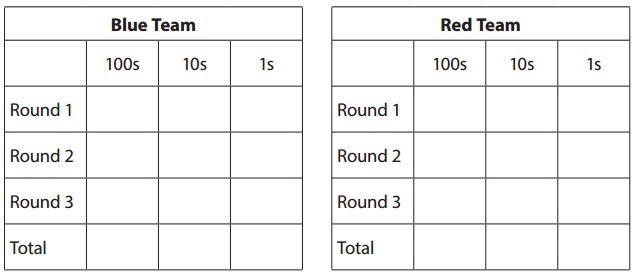
CHALLENGE Add the three scores for each team below. Then roll a more/less die to see who wins the entire game. Circle the winning team.
Answer:
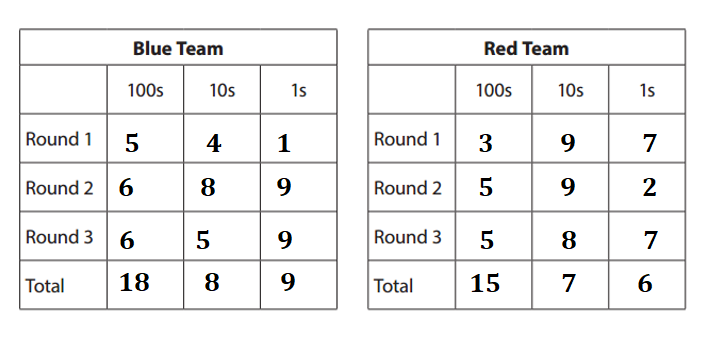
Explanation:
Round 1: 100s 10s 1s Total
Blue team = 5 4 1 = 541.
Red team = 3 9 7 = 397.
Round 2: 100s 10s 1s Total
Blue team = 6 8 9 = 689.
Red team = 5 9 2 = 592.
Round 3: 100s 10s 1s Total
Blue team = 6 5 9 = 659.
Red team = 5 8 7 = 587.
Blue Team total = 541 + 689 + 659 = 1,230 + 659 = 1,889.
Red Team total = 397 + 592 + 587 = 989 + 587 = 1,576.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 1 Session 5 Answer Key
5A Jump-a-Ten Game Board

Bridges in Mathematics Grade 2 Student Book Unit 5 Module 2 Session 1 Answer Key
Two Dimes & a Nickel
Question 1.
Write the name of the one coin that has the same value as the pennies in each of the counting frames below.
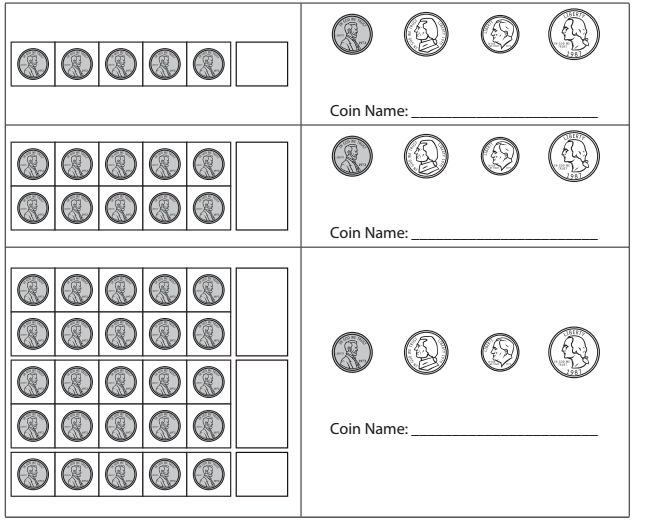
Answer:
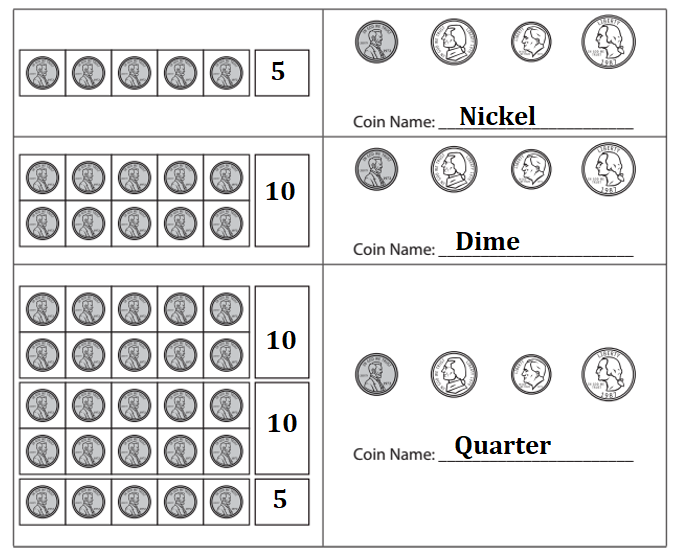
Explanation:
1 Penny = 1 cent = $0.01.
1 nickel = 5 cents = $0.05.
1 dime = 10 cents = $0.10.
1 quarter = 25 cents = $0.25.
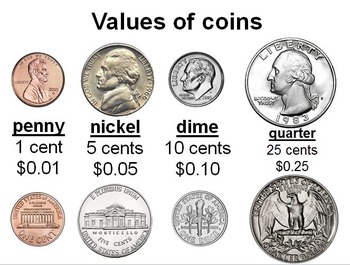
Question 2.
Use your coins to make six different combinations of 25¢. Do not use more than 10 pennies in any of the combinations. Record each one in the boxes below.

Answer:
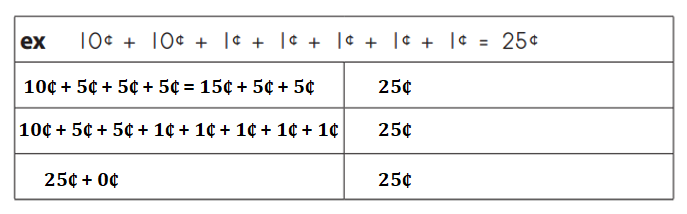
Explanation:
10¢ + 5¢ + 5¢ + 5¢ = 15¢ + 5¢ + 5¢
= 20¢ + 5¢
= 25¢.
10¢ + 5¢ + 5¢ + 1¢ + 1¢ + 1¢ + 1¢ + 1¢
= 15¢ + 5¢ + 1¢ + 1¢ + 1¢ + 1¢ + 1¢
= 20¢ + 1¢ + 1¢ + 1¢ + 1¢ + 1¢
= 21¢ + 1¢ + 1¢ + 1¢ + 1¢
= 22¢ + 1¢ + 1¢ + 1¢
= 23¢ + 1¢ + 1¢
= 24¢ + 1¢
= 25¢.
25¢ + 0¢
= 25¢.
Question 3.
Answer the questions and solve the problems about the pennies in this 25-frame.
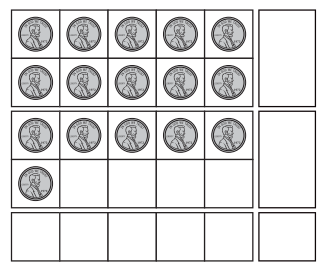
a. How many pennies are there in the frame?
Answer:
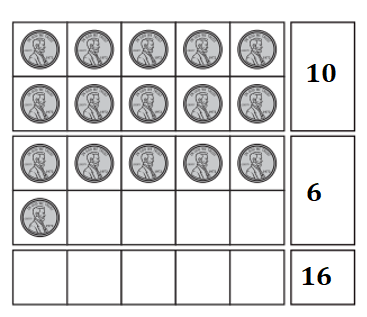
Explanation:
Number of pennies in the frame = 10 + 6
= 16.
b. Write an equation to show how you counted the pennies in the frame.
Answer:
Equation:
Total number of pennies in the frame = 10 + 6 = 16.
Explanation:
Number of pennies in one line = 10.
Number of pennies in second line = 6.
Total number of pennies in the frame = Number of pennies in one line + Number of pennies in second line
= 10 + 6
= 16.
c. Draw and label a combination of coins that has the same value as the pennies in this frame.
Answer:
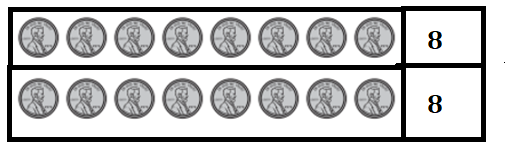
Explanation:
Number of pennies in one line = 8.
Number of pennies in second line = 8.
Total number of pennies in the frame = Number of pennies in one line + Number of pennies in second line
= 8 + 8
= 16.
d. How many more pennies would it take to make 25 in all? Show your work. Write the answer on the line.

It would take ___________ more pennies to make 25 in all.
Answer:
Number of more pennies needed = 9.
It would take 9 more pennies to make 25 in all.
Explanation:
Total pennies in all = 25.
Number of pennies in one line = 8.
Number of pennies in second line = 8.
Number of more pennies needed = Total pennies in all – (Number of pennies in one line + Number of pennies in second line)
= 25 – (8 + 8)
= 25 – 16
= 9.
Question 4.
Answer the questions and solve the problems about the pennies in this 25-frame.
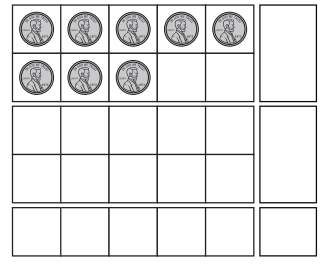
a. How many pennies are there in the frame?
Answer:
There are 8 pennies in the frame.
Explanation:
Number of pennies in the frame = 8.
=> There are 8 pennies in the frame.
b. Write an equation to show how you counted the pennies in the frame.
Answer:
Total number of pennies in all = 5 + 3 = 8.
Explanation:
Number of pennies in first row = 5.
Number of pennies in second row = 3.
Total number of pennies in all = Number of pennies in first row + Number of pennies in second row
= 5 + 3
= 8.
c. Draw and label a combination of coins that has the same value as the pennies in this frame.
Answer:
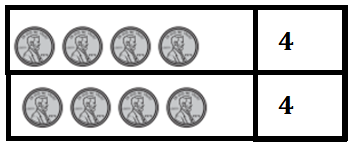
Explanation:
Number of pennies in first row = 4.
Number of pennies in second row = 4.
Total number of pennies in all = Number of pennies in first row + Number of pennies in second row
= 4 + 4
= 8.
d. How many more pennies would it take to make 25 in all? Show your work. Write the answer on the line.

It would take ___________ more pennies to make 25 in all.
Answer:
Number of more pennies needed = 17.
It would take 17 more pennies to make 25 in all.
Explanation:
Total pennies in all = 25.
Number of pennies in one line = 5.
Number of pennies in second line = 3.
Number of more pennies needed = Total pennies in all – (Number of pennies in one line + Number of pennies in second line)
= 25 – (5 + 3)
= 25 – 8
= 17.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 2 Session 2 Answer Key
5B Close to 25¢ Record Sheet

Bridges in Mathematics Grade 2 Student Book Unit 5 Module 2 Session 4 Answer Key
Pocketful of Coins
Question 1.
Jay and Sara are walking home from school and talking about how much money they have in their pockets. They hold out their hands to show the coins in their pockets.
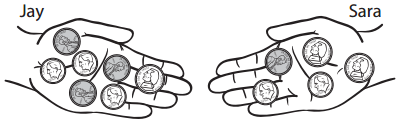
a. How much money does each child have in his or her hand?
Jay has ___________ ¢ Sara has ___________¢
Answer:
Total number of cents Jay has = 23.
Total number of cents Sara has = 21.
Jay has 23¢ Sara has 21¢.
Explanation:
Number of nickles Jay has = 4 = 4 × 5 cents = 20 cents.
Number of pennies Jay has = 3 = 3cents.
Total number of cents Jay has = Number of nickles Jay has + Number of pennies Jay has
= 20 + 3
= 23 cents.
Number of nickles Sara has = 4 = 4 × 5 cents = 20 cents.
Number of pennies Sara has = 1 = 1 cent.
Total number of cents Sara has = Number of nickles Sara has + Number of pennies Sara has
= 20 + 1
= 21 cents.
Conversion:
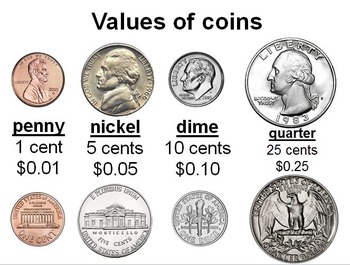
b. How much money do the two children have in all?
____________ ¢
Answer:
Total number of cents they have in all = 44.
44 ¢.
Explanation:
Total number of cents Jay has = 23.
Total number of cents Sara has = 21.
Total number of cents they have in all = Total number of cents Jay has + Total number of cents Sara has
= 23 + 21
= 44.
Question 2.
Lin and Sam are walking home from school and talking about how much money they have in their pockets. They hold out their hands to show the coins in their pockets.
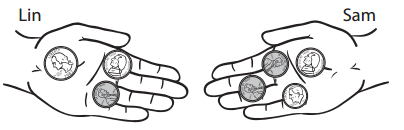
a. How much more money does Sam have than Lin? Show your work.
Answer:
6 cents more money Sam has than Lin.
Explanation:
Number of nickles Lin has = 1 = 1 × 5 cents = 5 cents.
Number of quarters Lin has = 1 = 1 × 25 cents = 25 cents.
Number of pennies Lin has = 1 = 1cent.
Total number of cents Lin has = Number of nickles Lin has + Number of quarters Lin has + Number of pennies Lin has
= 5 + 25 + 1
= 30 + 1
= 31 cents.
Number of dime Sam has = 1 = 1 × 10 cents = 10 cents.
Number of quarters Sam has = 1 = 1 × 25 cents = 25 cents.
Number of pennies Sam has = 2 = 2 cents.
Total number of cents Sam has = Number of dime Sam has + Number of quarters Sam has + Number of pennies Sam has
= 10 + 25 + 2
= 35 + 2
= 37 cents.
Difference:
Total number of cents Sam has – Total number of cents Lin has
= 37 – 31
= 6 cents.
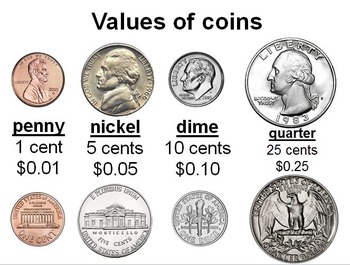
b. How much more money do Lin and Sam need together to make $1.00? Show your work.
Answer:
Number of cents they need more to make $1.00 = 32.
Explanation:
Total number of cents Sam has = 37.
Total number of cents Lin has = 31.
Total number of cents they have altogether = Total number of cents Sam has + Total number of cents Lin has
= 37 + 31
= 68.
Conversion:
1 dollar = 100 cents.
Number of cents they need more to make $1.00 = 100 cents – Total number of cents they have altogether
= 100 – 68
= 32 cents.
Question 3.
Ming has some money in his hand that he shows to Rosa. Rosa has some money in her hand, but she won’t show it to Ming. Together, they have 77¢.
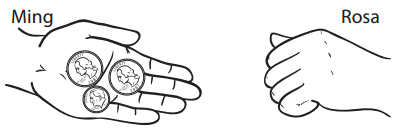
a. How much money does Rosa have in her hand? Show your work.
Answer:
Number of cents Rosa has = 57.
Explanation:
Number of nickels Ming has = 2 = 2 × 5 = 10 cents.
Number of dimes Ming has = 1 = 1 × 10 = 10 cents.
Total number of cents Ming has = Number of nickels Ming has + Number of dimes Ming has
= 10 + 10
= 20.
Total number of cents they have altogether = 77.
=> Number of cents Rosa has = Total number of cents they have altogether – Total number of cents Ming has
=> 77 – 20
=> 57.
b. Draw a picture to show what coins Rosa has in her hand.
(There is more than one possible combination. Show two or more if you like.)
Answer:

Explanation:
Number of cents Rosa has = 57.
Number of nickles Rosa has = 1= 1 × 5 = 5 cents.
Number of pennies Rosa has = 2 = 2 × 1 = 2 cents.
Number of quarters Rosa has = 2 = 2 × 25 = 50 cents.
Question 4.
Before school, Mom gave Eric 84 ¢ and told him to share the money fairly with his sister, Amber.
a. How much money will each child get? Use numbers, labeled sketches, and/or words to solve the problem. Show your work.
Each child will get ___________ ¢.
Answer:
Number of cents each gets = 42.
Each child will get 42 ¢.
Explanation:
Number of cents Mom gave Eric = 84.
Number of members to share the amount = 2.
Number of cents each gets = Number of cents Mom gave Eric ÷ Number of members to share the amount
= 84 ÷ 2
= 42.
b. How much more money do Eric and Amber need to make $1.00? Show your work.
Eric and Amber need ____________¢ to make $1.00.
Answer:
Number of cents more Eric and Amber need to make $1.00 = 58.
Eric and Amber need 58 ¢ to make $1.00.
Explanation:
Number of cents each gets = 42.
Conversion:
1 dollar = 100 cents.
=> Number of cents more Eric and Amber need to make $1.00 = 100 – Number of cents each gets
= 100 – 42
= 58.
Question 5.
CHALLENGE Jessie has exactly 10 coins in her pocket. They are worth 284 in all. Draw and label a picture to show the coins she has in her pocket.
Answer:
Number of coins she has in her pocket = 2 one dollar coins.
1 Half dollar coin.
4 Pennies coin.
3 Dime coins.
Explanation:
Number of coins in her pocket Jessie has exactly = 10.
Number of coins in all = 284.
Conversion:
one dollar coin = 100 ¢.
half dollar coin = 50 ¢.
Penny coin = 1 ¢.
Dime coin = 10 ¢.
Number of one dollar coin = 2 = 2 × 100 ¢ = 200 ¢.
Number of half dollar coin = 1 = 1 × 50 ¢ = 50 ¢.
Number of pennies coin = 4 = 4 × 1¢ = 4 ¢.
Number of dime coins = 3 = 3 × 10 ¢ = 30 ¢.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 2 Session 6 Answer Key
5D Three Spins to Win Record Sheet
Answer:
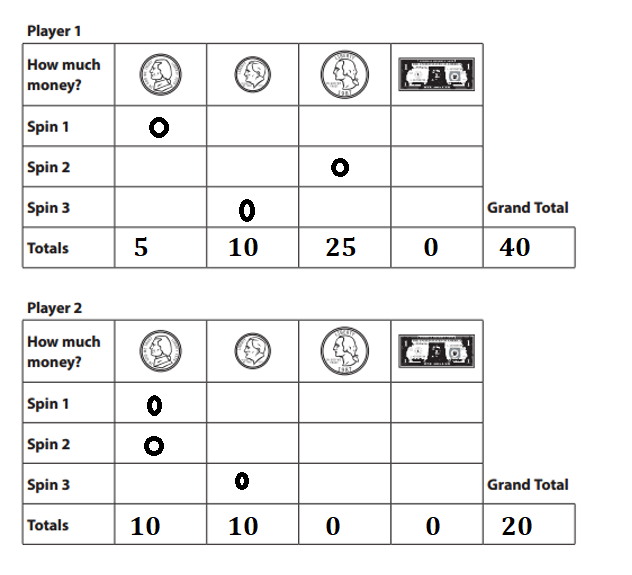
Explanation:
Player 1:
Spin 1: Nickle = 5 ¢.
Spin 2: Quarter = 25 ¢.
Spin 3: Dime = 10 ¢.
Grand total = 5 ¢ + 25 ¢+ 10 ¢ = 30 ¢ + 10 ¢ = 40 ¢.
Player 2:
Spin 1: Nickle = 5 ¢.
Spin 2: Nickle = 5 ¢.
Spin 3: Dime = 10 ¢.
Grand total = 5 ¢ + 5 ¢+ 10 ¢ = 10 ¢ + 10 ¢ = 20 ¢.
Conversion:
One dollar coin = 100 ¢.
Half dollar coin = 50 ¢.
Penny coin = 1 ¢.
Dime coin = 10 ¢.
Nickle coin = 5 ¢.
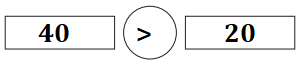
=> 40 cents is greater than 20 cents.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 3 Session 2 Answer Key
Measuring with Clip Chains
Question 1.
Measure five objects or distances with your clip chain. Record your work in the table below.
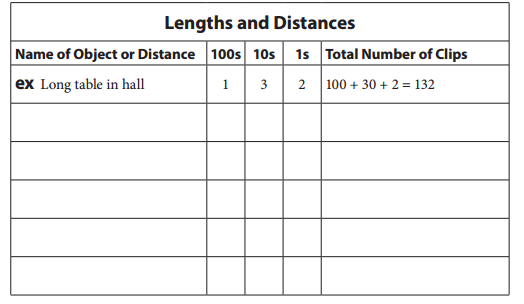
Answer:
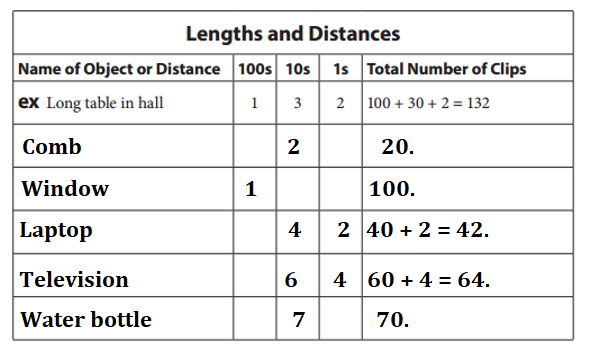
Explanation:
Five objects with your clip chain:
Comb – 2 × 10s = 20s.
Window = 1 × 100s = 100s.
Laptop = 4 × 10s + 2 × 1s = 40s + 2s = 42s.
Television: 6 × 10s + 4 × 1s = 60s + 4s = 64s.
Water bottle = 7 × 10s = 70s.
Question 2.
What was the longest object or distance you measured?
Answer:
The longest object I have measured is Window of 100 clips.
Explanation:
Five objects with your clip chain:
Comb – 2 × 10s = 20s.
Window = 1 × 100s = 100s.
Laptop = 4 × 10s + 2 × 1s = 40s + 2s = 42s.
Television: 6 × 10s + 4 × 1s = 60s + 4s = 64s.
Water bottle = 7 × 10s = 70s.
Question 3.
What was the shortest object or distance you measured?
Answer:
The shortest object I have measured is Comb is 20 clips.
Explanation:
Five objects with your clip chain:
Comb – 2 × 10s = 20s.
Window = 1 × 100s = 100s.
Laptop = 4 × 10s + 2 × 1s = 40s + 2s = 42s.
Television: 6 × 10s + 4 × 1s = 60s + 4s = 64s.
Water bottle = 7 × 10s = 70s.
Question 4.
Find the difference between the lengths of these two objects or distances. Show your work.
The difference between the longest and the shortest object or distance
I measured was _______________ clips.
Answer:
The difference between the longest and the shortest object or distance
I measured was 80 clips.
Explanation:
Five objects with your clip chain:
Comb – 2 × 10s = 20s.
Window = 1 × 100s = 100s.
Laptop = 4 × 10s + 2 × 1s = 40s + 2s = 42s.
Television: 6 × 10s + 4 × 1s = 60s + 4s = 64s.
Water bottle = 7 × 10s = 70s.
The shortest object I have measured is Comb is 20 clips.
The longest object I have measured is Window of 100 clips.
Difference:
The longest object I have measured is Window – The shortest object I have measured is Comb
= 100 clips – 20 clips
= 80 clips.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 3 Session 3 Answer Key
More Broken Chains
Question 1.
Oh no! Our paperclip chain broke! This is all we have left! Write the number on the blank card to show which clip is marked.
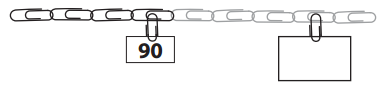
Answer:
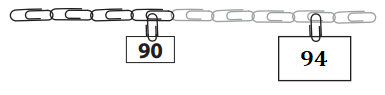
Explanation:
Number given of the clip = 90.
Number of clips away to find the unknown clip = 4.
=> Number of the clip to find = 90 + 4
= 94.
Question 2.
Here is another part of the chain. Write the numbers on the blank cards to show which clips are marked.

Answer:

Explanation:
Number given of the clip = 200.
Number of clips away to find the unknown clip to the right side = 4.
=> Number of the clip to find = 200 + 4
= 204.
Number of clips away to find the unknown clip to the left side = 4.
=> Number of the clip to find = 200 – 6
= 194.
Question 3.
There is one paperclip missing in each of these chains. Write the number in the box to show which one it is.
a.

Answer:

Explanation:
Number given of the clip = 110.
Number of clips away to find the unknown clip to the right side = 6.
=> Number of the clip to find = 110 + 6
= 116.
b.

Answer:

Explanation:
Number given of the clip = 355.
Number of clips away to find the unknown clip to the right side = 7.
=> Number of the clip to find = 355 – 7
= 348.
Question 4.
Use this chain to answer the questions below.

a. If you added 10 more clips to the end of the chain marked 103, what number would you use to label the paperclip?
Answer:
The number label the paperclip is 10.
Explanation:
Numbers given: 94 start – 103 end.
If you added 10 more clips to the end of the chain marked 103,
The number used to label the paperclip = 103 + 10
= 113 clips
=> 10s.
b. If you went backward 10 clips from the end of the chain marked 94, what number would you use to label the paperclip?
Answer:
The number label the paperclip is 10.
Explanation:
Numbers given: 94 start – 103 end.
If you went backward 10 clips from the end of the chain marked 94,
The number used to label the paperclip = 94 – 10
= 84 clips
=> 10s.
Question 5.
Fill in the blank box at the end of this chain to show which clip is marked. Then use the chain to answer the questions below.
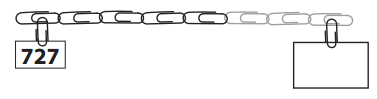
a. If you added 100 more clips to the end of the chain you just marked, what number would you use to label the paperclip?
Answer:
The number label the paperclip is 100.
Explanation:
Number given = 727.
If you added 100 more clips to the end of the chain you just marked,
=> Number used to label the paperclip = 727 + 100
=> 737.
=> 100 clips.
b. If you went backward 100 clips from the end of the chain marked 727, what number would you use to label the paperclip?
Answer:
The number label the paperclip is 100.
Explanation:
Number given = 727.
If you went backward 100 clips from the end of the chain marked 727,
=> Number used to label the paperclip = 727 – 100
=> 627.
=> 100 clips.
Question 6.
CHALLENGE The kids are trying to put all the pieces back together to make a chain of 1,000 paperclips. They added another section of 225 clips to the chain below. Did they reach 1,000? If not, how many more clips would they need to get to 1,000? Show all of your work.

Answer:
Number of more clips they need to get to 1,000 = 28.
Explanation:
Number of paperclips chain kids trying to put back together = 1,000.
Number of clips to the chain they added another section = 225.
Number of clips to the chain they given = 747.
Number of clips they have now = Number of clips to the chain they given + Number of clips to the chain they added another section
= 747 + 225
= 972.
Number of more clips they need to get to 1,000 = Number of paperclips chain kids trying to put back together – Number of clips they have now
= 1,000 – 972
= 28.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 3 Session 4 Answer Key
Bird’s Eye View
Imagine that you are looking at a chain of 1,000 paperclips from the top of a very high tree. You can see the labels on the chain but not the paperclips.
Question 1.
Fill in the missing numbers on these chains.
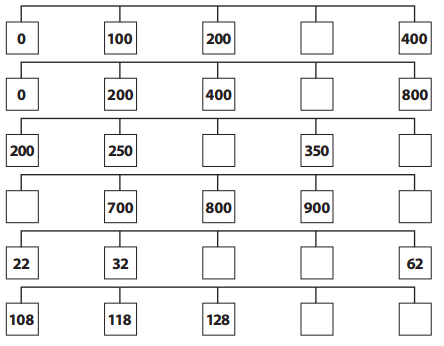
Answer:
Missing numbers:
Explanation:
1. Difference: 100 – 0 = 100.
Missing number = 400 – 100 = 300.
2. Difference: 200 – 0 = 200.
Missing number = 800 – 200 = 600.
3. Difference: 250 – 200 = 50.
Missing number = 250 + 50 = 300.
Missing number = 350 + 50 = 400.
4. Difference: 800 – 700 = 100.
Missing number = 700 – 100 = 600.
Missing number = 900 + 100 = 1,000.
5. Difference: 32 – 22 = 10.
Missing number = 32 + 10 = 42.
Missing number = 42 + 10 = 52.
6. Difference: 128 – 118 = 10.
Missing number = 128 + 10 = 138.
Missing number = 148 + 10 = 158.
Question 2.
Now imagine that your friend is down on the ground counting the paperclips in the chain. Right now, he is at paperclip number 125. Fill in the boxes below to show where he would be if…
a. He counted 100 more paperclips.
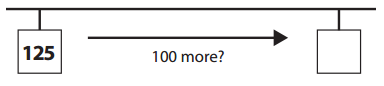
Answer:
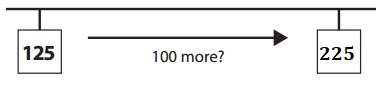
Explanation:
Number of paperclip he is at = 125.
He counted 100 more paperclips.
=> Number of paperclip he would be = Number of paperclip he is at + 100
= 125 + 100
= 225.
b. He counted 300 more paperclips.
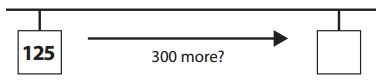
Answer:
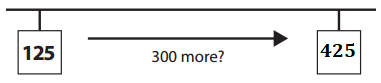
Explanation:
Number of paperclip he is at = 125.
He counted 300 more paperclips.
=> Number of paperclip he would be = Number of paperclip he is at + 300
= 125 + 300
= 425.
c. He counted back 10 paperclips.
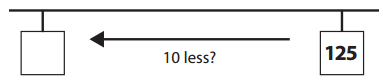
Answer:
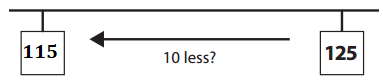
Explanation:
Number of paperclip he is at = 125.
He counted back 10 paperclips.
=> Number of paperclip he would be = Number of paperclip he is at – 10
= 125 – 10
= 115.
d. He counted back 25 paperclips.
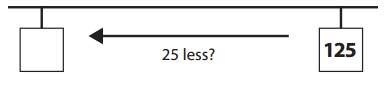
Answer:
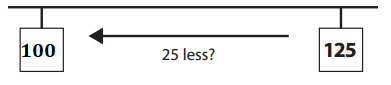
Explanation:
Number of paperclip he is at = 125.
He counted back 25 paperclips.
=> Number of paperclip he would be = Number of paperclip he is at – 25
= 125 – 25
= 100.
Question 3.
Now your friend is at paperclip number 305. Fill in the boxes below to show where he would be if…
a. He counted 100 more paperclips.

Answer:

Explanation:
Number of paperclip he is at = 305.
He counted 100 more paperclips.
=> Number of paperclip he would be = Number of paperclip he is at + 100
= 305 + 100
= 405.
b. He counted 10 more paperclips and then 10 more paperclips after that?
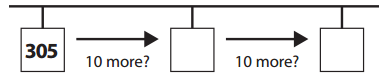
Answer:
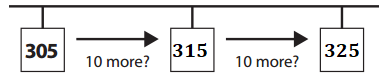
Explanation:
Number of paperclip he is at = 305.
He counted 10 more paperclips.
=> Number of paperclip he would be = Number of paperclip he is at + 10
= 305 + 10
= 315.
He counted 10 more paperclips.
=> Number of paperclip he would be = Number of paperclip he would be + 10
= 315 + 10
= 325.
Question 4.
Here is a picture of a paperclip chain from 0 to 1,000. Fill in the missing numbers.

Answer:

Explanation:
Number of paperclip started = 0.
Given paperclips numbers: 0, 100, ___ , 300, ____, 500, 600, _____, 800, 9+00, 1,000.
Difference:
100 – 0 = 100.
Missing numbers:
=> Number of paperclip he would be = 100 + Difference
= 100 + 100
= 200.
=> 300 + Difference = 300 + 100 = 400.
=> 600 + Difference = 600 + 100 = 700.
Question 5.
Here is a picture of a paperclip chain from 0 to 1,000. Write the numbers 500, 800, and 100 in the boxes where they belong.

Answer:

Explanation:
Given paperclips:
0, _____, ______, _____, 1,000.
Numbers given: 500, 800, and 100
=> 0, 100, 500, 800, 1,000.
=> Least to greatest order.
Question 6.
Here is a picture of a paperclip chain from 400 to 1,000. Write the numbers 900, 700, 800, and 500 in the boxes where they belong.

Answer:

Explanation:
Given paperclips:
400, _____, 600, _____, _____, _____, 1,000.
Numbers given: 900, 700, 800, and 500
=> 400, 500, 600, 700, 800, 900, 1,000.
=> Least to greatest order.
Question 7.
CHALLENGE Mark and label each of the number lines below with the numbers listed in the boxes.
a.

Answer:
Given paperclips:
200, _____, 400.
Numbers given: 300, 250, and 350
=> 200, 250, 300, 350, 400.
=> Least to greatest order.
b.

Answer:
Given paperclips:
200, _____, 300.
Numbers given: 225, 250, and 275.
=> 200, 225, 250, 275, 300.
=> Least to greatest order.
Question 8.
CHALLENGE Fill in the missing numbers on the number lines below.
Answer:
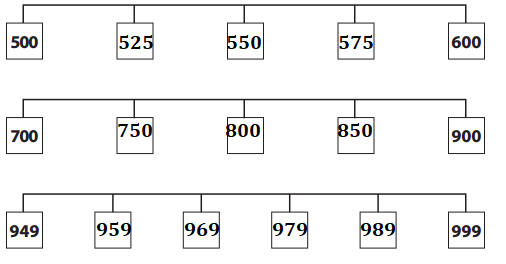
Explanation:
Missing numbers:
1. 500, ____ , _____ , ____ , 600.
Three equal intervals between 500 to 600.
=> Difference: 600 – 500 = 100.
100 ÷ 4 = 25.
500, 525, 550, 575, 600.
2. 700, ____ , _____ , ____ , 900.
Four equal intervals between 700 to 900.
=> Difference: 900 – 700 = 200.
200 ÷ 4 = 50.
700, 750, 800, 850, 900.
3. 949, ____ , _____ , ____ , ____ , 999.
Five equal intervals between 949 to 999.
=> 999 – 949 = 50.
=> 50 ÷ 5 = 10.
949, 959, 969, 979, 989, 999.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 4 Session 2 Answer Key
Unifix Cube Sequence Problems
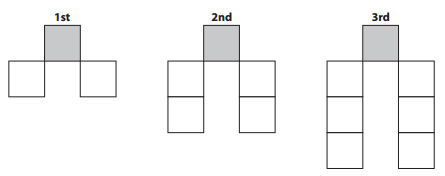
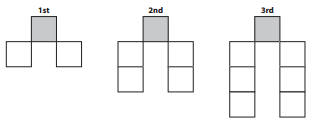
Here are the first 3 arrangements in a sequence of Unifix cubes:
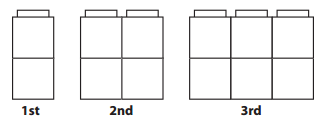
Question 1.
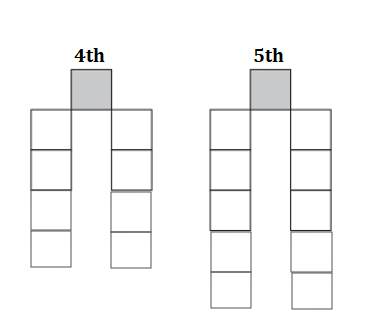
Build and draw the 4th and 5th arrangements in the sequence.
Answer:
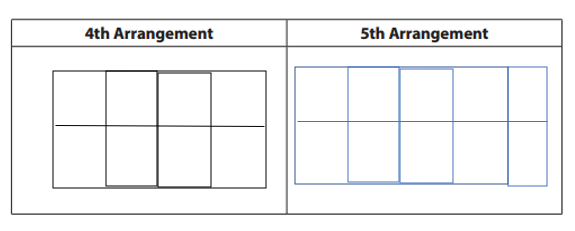
Explanation:
The first 3 arrangements in a sequence of Unifix cubes:
1st: 2.
2nd: 4.
Difference:
4 – 2 = 2.
3rd: 6.
4th: 8.
5th: 10.
Question 2.
Use words and/or numbers to write 3 observations about this sequence so far.
a _____________________
b _____________________
c _____________________
Answer:
Observation:
a. It is observed that the difference between the numbers is two.
b. All numbers are even.
c. All numbers are multiples of 2 .
Explanation:
The first 3 arrangements in a sequence of Unifix cubes:
1st: 2.
2nd: 4.
Difference:
4 – 2 = 2.
3rd: 6.
4th: 8.
5th: 10.
Observation:
It is observed that the difference between the numbers is two.
All numbers are even.
All numbers are multiples of 2 .
Question 3.
Sam says this sequence is a growing pattern. Do you agree with Sam? Why or why not?
Answer:
Yes, I agree with Sam because the pattern is increasing by interval of 2 between the numbers each.
Explanation:
The first 3 arrangements in a sequence of Unifix cubes:
1st: 2.
2nd: 4.
3rd: 6.
4th: 8.
5th: 10.
Question 4.
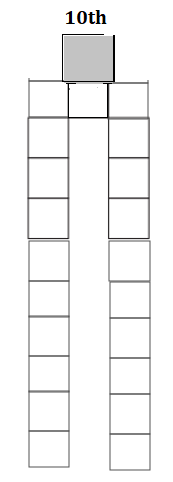
Draw the 10th arrangement in this sequence. You can build it first, or you can just draw how it will look.
Answer:
The 10th arrangement in this sequence is 20.
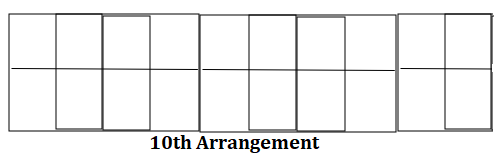
Explanation:
The first 10 arrangements in a sequence of Unifix cubes:
1st: 2.
2nd: 4.
3rd: 6.
4th: 8.
5th: 10.
6th : 12.
7th: 14.
8th: 16.
9th: 18.
10th: 20.
Question 5.
How many cubes did it take to make the 10th arrangement in the sequence?
It took ______________ cubes to make the 10th arrangement.
Answer:
20 cubes are used to make the 10th arrangement in the sequence.
It took 20 cubes to make the 10th arrangement.
Explanation:
Number of cubes are used to make the 10th arrangement in the sequence = ??
=> 20 cubes.
Question 6.
CHALLENGE How many cubes would it take to make the 100th arrangement in this sequence? How do you know?
Answer:
200 cubes it would take to make the 100th arrangement in this sequence because difference into the arrangement number in the sequence gives the number of cubes.
Explanation:
Number of cubes are used to make the 100th arrangement in the sequence = ??
=> 100 × Difference
=> 100 × 2
=> 200 cubes.
Question 7.
CHALLENGE How many cubes would it take to make the 149 th arrangement in this sequence? Show your work.
Answer:
298 cubes it would take to make the 149th arrangement in this sequence because difference into the arrangement number in the sequence gives the number of cubes.
Explanation:
Number of cubes are used to make the 149th arrangement in the sequence = ??
=> 149 × Difference
=> 149 × 2
=> 298 cubes.
Bridges in Mathematics Grade 2 Student Book Unit 5 Module 4 Session 4 Answer Key
Tile Sequence Problems
Here are the first 3 arrangements in a tile sequence:
Question 1.
Build and draw the 4th and 5th arrangements in the sequence.

Answer:
Explanation:
First five arrangements in the sequence:
1st: 3.
2nd: 5.
Difference: 5 – 3 = 2.
3rd: 7.
4th: 9.
5th: 11.
Question 2.
Use words and/or numbers to write 3 observations about this sequence so far.
a _______________________
b _______________________
c _______________________
Answer:
Observation:
a. It is observed that the difference between the numbers is two.
b. All numbers are odd.
c. All numbers are prime numbers.
Explanation:
First five arrangements in the sequence:
1st: 3.
2nd: 5.
3rd: 7.
4th: 9.
5th: 11.
Observation:
It is observed that the difference between the numbers is two.
All numbers are odd.
All numbers are prime numbers.
Question 3.
Draw the 10th arrangement in this sequence. You can build it first, or you can just draw how it will look. (Hint: Make your sketch sideways to get it to fit.)
Answer:
The 10th arrangement in this sequence:
Explanation:
The 10th arrangement in this sequence:
1st: 3.
2nd: 5.
3rd: 7.
4th: 9.
5th: 11.
6th: 13.
7th: 15.
8th: 17.
9th: 19.
10th: 21.
Question 4.
Still thinking about this sequence:
a. How many tiles did it take to make the 5th arrangement?
Answer:
11 tiles are used to make the 5th arrangement.
Explanation:
Number of tiles are used to make the 5th arrangement = ??
=> 11 tiles.
1st: 3.
2nd: 5.
3rd: 7.
4th: 9.
5th: 11.
6th: 13.
7th: 15.
8th: 17.
9th: 19.
10th: 21.
b. How many tiles did it take to make the 10th arrangement?
Answer:
21 tiles are used to make the 10th arrangement.
Explanation:
Number of tiles are used to make the 10th arrangement = ??
=> 21 tiles.
1st: 3.
2nd: 5.
3rd: 7.
4th: 9.
5th: 11.
6th: 13.
7th: 15.
8th: 17.
9th: 19.
10th: 21.
c. How many tiles would it take to make the 20th arrangement?
Answer:
39 tiles are used to make the 20th arrangement.
Explanation:
Number of tiles are used to make the 21th arrangement = ??
=> 39 tiles.
1st: 3.
2nd: 5.
3rd: 7.
4th: 9.
5th: 11.
6th: 13.
7th: 15.
8th: 17.
9th: 19.
10th: 21.
11th: 23.
12th: 25.
13th: 26.
14th: 27.
15th: 29.
16th: 31.
17th: 33.
18th: 35.
19th: 37.
20th: 39.
Question 5.
CHALLENGE Solve these problems about the tile sequence shown above. Show your work for each.
a. How many tiles would it take to make the 26th arrangement?
Answer:
51 tiles it would take to make the 26th arrangement.
Explanation:
20th arrangement: 39.
21st: 41.
22nd: 43.
23rd: 45.
24th: 47.
25th: 49.
26th: 51.
b. How many tiles would it take to make the 34th arrangement?
Answer:
67 tiles it would take to make the 34th arrangement.
Explanation:
Arrangements:
26th: 51.
27th: 53.
28th: 55.
29th: 57.
30th: 59.
31st: 61.
32nd: 63.
33rd: 65.
34th: 67.
c. Which arrangement would take 31 tiles to make?
Answer:
16th arrangement would take 31 tiles to make.
Explanation:
Arrangements:
16th: 31.
17th: 33.
18th: 35.
19th: 37.
20th: 39.
Question 6.
CHALLENGE What do you have to do to figure out how many tiles it takes to make any arrangement in the sequence above?
Answer:
We need to first figure out the tiles number to know the arrangement in the sequence above.
Explanation:
For checking how many tiles to make any arrangement in the sequence above we need to first figure out the tiles number to know the arrangement.