Big Ideas Math Geometry Answers Chapter 8 Similarity

Studying & Practicing Math Geometry would be done in a fun learning process for a better understanding of the concepts. So, the best guide to prepare math in a fun learning way is our provided Big Ideas Math Geometry Answers Chapter 8 Similarity Guide. In this study guide, you will discover various exercise questions, chapter reviews, tests, chapter practices, cumulative assessment, etc. to learn all topics of chapter 8 similarity. These questions and answers are explained by the subject experts in a simple manner to make students learn so easily & score maximum marks in the exams.

Big Ideas Math Book Geometry Answer Key Chapter 8 Similarity

BIM Geometry Book Solutions are available for all chapters along with Chapter 8 Similarity on our website. So, make sure to check all the chapters of Big Ideas Math Book Geometry Answer Key and learn the subject thoroughly. Based on the common core 2019 curriculum, these Big Ideas Math Geometry Answers Chapter 8 Similarity are prepared. So, students can instantly take homework help from BIM Geometry Ch 8 Similarity Answers. Simply tap on the below direct links and refer to the solutions covered in the Big Ideas Math Book Geometry Answer Key Chapter 8 Similarity Guide.

• Similarity Maintaining Mathematical Proficiency – Page 415
• Similarity Mathematical Practices – Page 416
• 8.1 Similar Polygons – Page 417
• Lesson 8.1 Similar Polygons – Page (418-426)
• Exercise 8.1 Similar Polygons – Page (423-426)
• 8.2 Proving Triangle Similarity by AA – Page 427
• Lesson 8.2 Proving Triangle Similarity by AA – Page (428-432)
• Exercise 8.2 Proving Triangle Similarity by AA – Page (431-432)
• 8.1 & 8.2 Quiz – Page 434
• 8.3 Proving Triangle Similarity by SSS and SAS – Page 435
• Lesson 8.3 Proving Triangle Similarity by SSS and SAS – Page (436-444)
• Exercise 8.3 Proving Triangle Similarity by SSS and SAS – Page (441-444)
• 8.4 Proportionality Theorems – Page 445
• Lesson 8.4 Proportionality Theorems – Page (446-452)
• Exercise 8.4 Proportionality Theorems – Page (450-452)
• Similarity Chapter Review – Page (454-456)
• Similarity Chapter Test – Page 457
• Similarity Cumulative Assessment – Page (458-459)

Similarity Maintaining Mathematical Proficiency

Tell whether the ratios form a proportion.

Question 1.
\(\frac{5}{3}, \frac{35}{21}\)

Answer:
Yes, the ratios \(\frac{5}{3}, \frac{35}{21}\) form a proportion.

Explanation:
A proportion means two ratios are equal.
So, cross product of \(\frac{5}{3}, \frac{35}{21}\) is 21 x 5 = 105 = 35 x 3
Therefore, \(\frac{5}{3}, \frac{35}{21}\) form a proportion.

Question 2.
\(\frac{9}{24}, \frac{24}{64}\)

Answer:
Yes, the ratios \(\frac{9}{24}, \frac{24}{64}\) form a proportion.

Explanation:
If the cross product of two ratios is equal, then it forms a proportion.
So, 24 x 24 = 576 = 64 x 9
Therefore, the ratios \(\frac{9}{24}, \frac{24}{64}\) form a proportion.

Question 3.
\(\frac{8}{56}, \frac{6}{28}\)

Answer:
The ratios \(\frac{8}{56}, \frac{6}{28}\) do not form a proportion.

Explanation:
If the cross product of two ratios is equal, then it forms a proportion.
So, 56 x 6 = 336, 28 x 8 = 224
Therefore, the ratios \(\frac{8}{56}, \frac{6}{28}\) do not form a proportion.

Question 4.
\(\frac{18}{4}, \frac{27}{9}\)

Answer:
The ratios \(\frac{18}{4}, \frac{27}{9}\) do not form a proportion.

Explanation:
If the cross product of two ratios is equal, then it forms a proportion.
So, 9 x 18 = 162, 27 x 4 = 108
Therefore, the ratios \(\frac{18}{4}, \frac{27}{9}\) do not form a proportion.

Question 5.
\(\frac{15}{21}, \frac{55}{77}\)

Answer:
The ratios \(\frac{15}{21}, \frac{55}{77}\) form a proportion.

Explanation:
If the cross product of two ratios is equal, then it forms a proportion.
So, 15 x 77 = 1155, 55 x 21 = 1155
Therefore, the ratios \(\frac{15}{21}, \frac{55}{77}\) form a proportion.

Question 6.
\(\frac{26}{8}, \frac{39}{12}\)

Answer:
The ratios \(\frac{26}{8}, \frac{39}{12}\) form a proportion.

Explanation:
If the cross product of two ratios is equal, then it forms a proportion.
So, 26 x 12 = 312, 39 x 8 = 312
Therefore, the ratios \(\frac{26}{8}, \frac{39}{12}\) form a proportion.

Find the scale factor of the dilation.

Question 7.

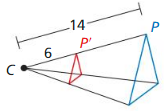
Answer:
k = \(\frac { 3 }{ 7 } \)

Explanation:
The scale factor k = \(\frac { CP’ }{ CP } \)
= \(\frac { 6 }{ 14 } \)
= \(\frac { 3 }{ 7 } \)

Question 8.

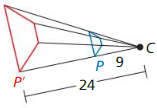
Answer:
k = \(\frac { 3 }{ 8 } \)

Explanation:
The scale factor k = \(\frac { CP }{ CP’ } \)
= \(\frac { 9 }{ 24 } \)
= \(\frac { 3 }{ 8 } \)

Question 9.

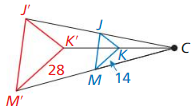
Answer:
k = \(\frac { 1 }{ 2 } \)

Explanation:
The scale factor k = \(\frac { MK }{ M’K’ } \)
= \(\frac { 14 }{ 28 } \)
= \(\frac { 1 }{ 2 } \)

Question 10.
ABSTRACT REASONING
If ratio X and ratio Y form a proportion and ratio Y and ratio Z form a proportion, do ratio X and ratio Z form a proportion? Explain our reasoning.

Answer:
Yes, ratio X and ratio Z form a proportion.

Explanation:
If ratios are proportional means they are equal.
So, ratio X and ratio Y form a proportion that means X = Y
ratio Y and ratio Z form a proportion that means Y = Z
From the above two equations, we can say that X = Z
So, ratio X and ratio Z also form a proportion.

Similarity Mathematical Practices

Monitoring Progress

Question 1.
Find the perimeter and area of the image when the trapezoid is dilated by a scale factor of
(a) 2, (b) 3, and (c) 4.

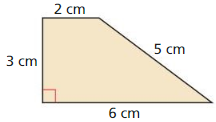
Answer:
(a) Perimeter is 32 cm, area is 48 sq cm.
(b) Perimeter is 48 cm, the area is 108 sq cm.
(c) Perimeter is 64 cm, the area is 192 sq cm.

Explanation:
The perimeter of trapezoid P = 2 + 5 + 6 + 3 = 16 cm
Area of trapezoid A = \(\frac { (2 + 6)3 }{ 2 } \)
= \(\frac { 3(8) }{ 2 } \)
= \(\frac { 24 }{ 2 } \)
= 12 sq cm
(a) If scale factor k = 2, then
Perimeter = kP
= 2 x 16 = 32
Area = k²A
= 2² x 12
= 4 x 12
= 48
(b) If scale factor k = 3, then,
Perimeter = kP
= 3 x 16 = 48 cm
Area = k²A
= 3² x 12 = 9 x 12 = 108
(c) If scale factor k = 4, then
Perimeter = kP
= 4 x 16 = 64
Area = k²A
= 4² x 12 = 16 x 12 = 192

Question 2.
Find the perimeter and area of the image when the parallelogram is dilated by a scale factor of
(a) 2, (b) 3, and (c) \(\frac{1}{2}\)

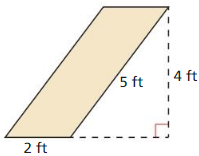
Answer:
(a) Perimeter is 28 ft, area is 32 sq ft
(b) Perimeter is 42 ft, area is 72 sq ft
(c) Perimeter is 7 ft, area is 2 sq ft

Explanation:
Perimeter of parallelogram P = 2(2 + 5) = 7 x 2 = 14 ft
Area of the parallelogram = 2 x 4 = 8 sq ft
(a) If scale factor k = 2, then
Perimeter = kP
= 2 x 14 = 28
Area = k²A
= 2² x 8 = 4 x 8 = 32
(b) If scale factor k = 3, then
Perimeter = kP
= 3 x 14 = 42
Area = k²A
= 3² x 8 = 72
(c) If scale factor k = \(\frac{1}{2}\), then
Perimeter = kP
= \(\frac{1}{2}\) x 14 = 7
Area = k²A
= \(\frac{1}{2²}\) x 8 = \(\frac{1}{4}\) x 8 = 2

Question 3.
A rectangular prism is 3 inches wide, 4 inches long, and 5 inches tall. Find the surface area and volume of the image of the prism when it is dilated by a scale factor of
(a) 2, (b) 3, and (c) 4.

Answer:
(a) Surface area is 376 sq in, volume is 480 cubic in
(b) Surface area is 846 sq in, volume is 1620 cubic in
(c) Surface area is 1504 sq in, volume is 3840 cubic in

Explanation:
The surface area of the rectangular prism A = 2(3 x 4 + 4 x 5 + 5 x 3)
= 2(12 + 20 + 15) = 2(47) = 94 in
Volume of the rectangular prism V = 3 x 4 x 5 = 60 in³
(a) If the scale factor k = 2, then
Surface Area = k²A
= 2² x 94 = 4 x 94 = 376 sq in
Volume = k³V
= 2³ x 60 = 8 x 60 = 480 cubic in
(b) If the scale factor k = 3, then
Surface Area = k²A
= 3² x 94 = 9 x 94 = 846
Volume = k³V
= 3³ x 60 = 27 x 60 = 1620
(c) If the scale factor k = 4, then
Surface Area = k²A
= 4² x 94 = 16 x 94 = 1504
Volume = k³V
= 4³ x 60 = 64 x 60 = 3840

8.1 Similar Polygons

Exploration 1

Comparing Triangles after a Dilation

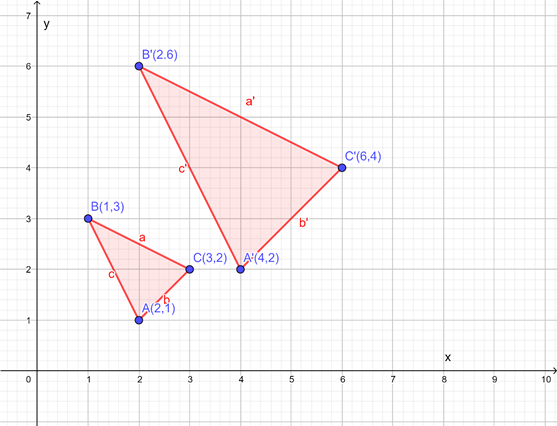
Work with a partner: Use dynamic geometry software to draw any ∆ABC. Dilate ∆ABC to form a similar ∆A’B’C’ using an scale factor k and an center of dilation.

a. Compare the corresponding angles of ∆A’B’C and ∆ABC.
Answer:
Comparing the coordinates side lengths, and angle measures ∆A’B’C and ∆ABC
1. Comparing the coordinates of ∆ABC and ∆A’B’C’
A(2, 1) → A'(4, 2)
B(1, 3) → B'(2, 6)
C(3, 2) → C'(6, 4)
2. Comparing the side length of ∆ABC and ∆A’B’C’
a(2.24) → d'(4.47)
b(1.41) → b'(2.83)
c(2.24) → c'(4.47)
3. Comparing the angle of ∆ABC and ∆A’B’C’
∠A(71.57) = ∠A'(71.57)
∠B(36.87) = ∠B'(36.87)
∠C(71.57) = ∠C'(71.57)

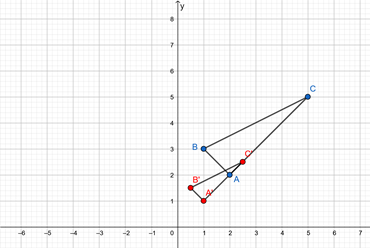
b. Find the ratios of the lengths of the sides of ∆A’B’C’ to the lengths of the corresponding sides of ∆ABC. What do you observe?
Answer:
Let the coordinates of the triangle to be A(2,2),B(1,3) and C(5,5). Plot these points on a coordinate plane to form a triangle ΔABC.
A(2, 2) = A'(1, 1)
B(1, 3) = B'(1/2, 3/2)
C(5, 5) = C'(5/2, 5/2)

c. Repeat parts (a) and (b) for several other triangles, scale factors, and centers of dilation. Do you obtain similar results?
Answer:
From the newly transformed triangles in part (a) and (b), side lengths of the triangles are changed by the scale factor of k and angle measures remain the same for both of the triangles ΔABC.

Exploration 2

Comparing Triangles after a Dilation

Work with a partner: Use dynamic geometry Software to draw any ∆ABC. Dilate ∆ABC to form a similar ∆A’B’C’ using any scale factor k and any center of dilation.

a. Compare the perimeters of ∆A’B’C and ∆ABC. What do you observe?
Answer:

b. Compare the areas of ∆A’B’C’ and ∆ABC. What do you observe?
Answer:

c. Repeat parts (a) and (b) for several other triangles, scale factors, and centers of dilation. Do you obtain similar results?
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:

Communicate Your Answer

Question 3.
How are similar polygons related?

Answer:
if two polygons are similar means they have the same shape, corresponding angles are congruent and the ratios of lengths of their corresponding sides are equal. The common ratio is called the scale factor.

Question 4.
A ∆RST is dilated by a scale factor of 3 to form ∆R’S’T’. The area of ∆RST is 1 square inch. What is the area of ∆R’S’T’?

Answer:
Area of ∆R’S’T’ = 9 sq in

Explanation:
Given that,
Area of ∆RST = 1 sq inch
Scale factor k = 3
Area of ∆R’S’T’ = k² x Area of ∆RST
= 3² x 1 = 9 x 1 = 9

Lesson 8.1 Similar Polygons

Monitoring Progress

Question 1.
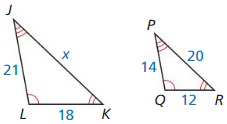
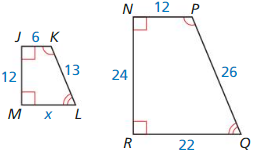
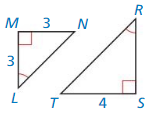
In the diagram, ∆JKL ~ ∆PQR. Find the scale factor from ∆JKL to ∆PQR. Then list all pairs of congruent angles and write the ratios of the corresponding side lengths in a statement of proportionality.

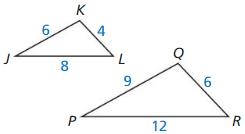
Answer:
The pairs of congruent angles are ∠K = ∠Q, ∠J = ∠P, ∠ L = ∠R
The scale factor is \(\frac { 3 }{ 2 } \)
The ratios of the corresponding side lengths in a statement of proportionality are \(\frac { PQ }{ JK } = \frac { PR }{ JL } = \frac { QR }{ LK } \)

Explanation:
Given that,
∆JKL ~ ∆PQR
The pairs of congruent angles are ∠K = ∠Q, ∠J = ∠P, ∠ L = ∠R
To find the scale factor,
\(\frac { PQ }{ JK } = \frac { 9 }{ 6 } \) = \(\frac { 3 }{ 2 } \), \(\frac { PR }{ JL } = \frac { 12 }{ 8 } \) = \(\frac { 3 }{ 2 } \), \(\frac { QR }{ LK } = \frac { 6 }{ 4 } \) = \(\frac { 3 }{ 2 } \)
So, the scale factor is \(\frac { 3 }{ 2 } \)

Question 2.
Find the value of x.

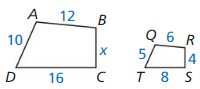
ABCD ~ QRST

Answer:
x = 2

Explanation:
The triangles are similar, so corresponding side lengths are proportional.
\(\frac { RS }{ BC } \) = \(\frac { AB }{ QR } \)
\(\frac { 4 }{ x } \) = \(\frac { 12 }{ 6 } \)
\(\frac { 4 }{ x } \) = 2
4 = 2x
x = 2

Question 3.
Find KM

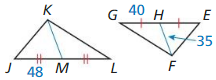
∆JKL ~ ∆EFG

Answer:
KM = 42

Explanation:
Scale factor = \(\frac { JM }{ GH } \)
= \(\frac { 48 }{ 40 } \)
= \(\frac { 6 }{ 5 } \)
Because the ratio of the lengths of the altitudes in similar triangles is equal to the scale factor, you can write the following proportion
\(\frac { KM }{ HF } \) = \(\frac { 6 }{ 5 } \)
\(\frac { KM }{ 35 } \) = \(\frac { 6 }{ 5 } \)
KM = \(\frac { 6 }{ 5 } \) x 35
KM = 42

Question 4.
The two gazebos shown are similar pentagons. Find the perimeter of Gazebo A.

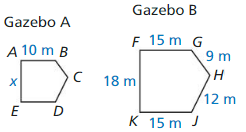
Answer:
Perimeter of Gazebo A = 46 m

Explanation:
Scale factor = \(\frac { AB }{ FG } \)
= \(\frac { 10 }{ 15 } \)
= \(\frac { 2 }{ 3 } \)
So, \(\frac { AE }{ FK } \) = \(\frac { 2 }{ 3 } \)
\(\frac { x }{ 18 } \) = \(\frac { 2 }{ 3 } \)
x = 12
\(\frac { ED }{ KJ } \) = \(\frac { 2 }{ 3 } \)
\(\frac { ED }{ 15 } \) = \(\frac { 2 }{ 3 } \)
ED = 10
\(\frac { DC }{ JH } \) = \(\frac { 2 }{ 3 } \)
\(\frac { DC }{ 12 } \) = \(\frac { 2 }{ 3 } \)
DC = 8
\(\frac { BC }{ GH } \) = \(\frac { 2 }{ 3 } \)
\(\frac { BC }{ 9 } \) = \(\frac { 2 }{ 3 } \)
BC = 6
Therefore, perimeter = 6 + 8 + 10 + 12 + 10 = 46

Question 5.
In the diagram, GHJK ~ LMNP. Find the area of LMNP.

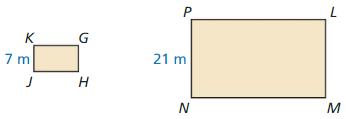
Area of GHJK = 84m²

Answer:
Area of LMNP = 756 m²

Explanation:
As shapes are similar, their corresponding side lengths are proportional.
Scale Factor k = \(\frac { NP }{ JK } \)
= \(\frac { 21 }{ 7 } \)
= 3
Area of LMNP = k² x Area of GHJK
= 3² x 84
= 756 m²

Question 6.
Decide whether the hexagons in Tile Design 1 are similar. Explain.

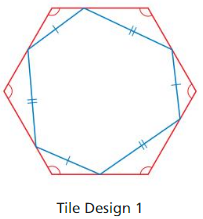
Answer: Both the hexagons are different. On the outer side of the hexagon, all the sides are equal. In the inside hexagon among the 6-sided 3 sides are different.

Question 7.
Decide whether the hexagons in Tile Design 2 are similar. Explain.

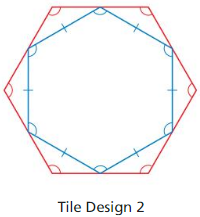
Answer: Both the hexagons are similar. Because all the sides of the outer hexagon are equal and all the sides of the inner hexagon are also equal.

Exercise 8.1 Similar Polygons

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
For two figures to be similar, the corresponding angles must be ____________ . and the corresponding side lengths must be _____________ .

Answer:

Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

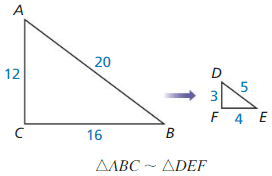
What is the scale factor?
Answer:
Scale Factor = \(\frac{image-length}{actual-length}\)
= \(\frac{3}{12}\)= \(\frac{4}{16}\)= \(\frac{5}{20}\)
= \(\frac{1}{4}\)

What is the ratio of their areas?

Answer:

What is the ratio of their corresponding side lengths?
Answer:

What is the ratio of their perimeters?
Answer:

Monitoring Progress and Modeling with Mathematics

In Exercises 3 and 4, find the scale factor. Then list all pairs of congruent angles and write the ratios of the corresponding side lengths in a statement of proportionality.

Question 3.
∆ABC ~ ∆LMN

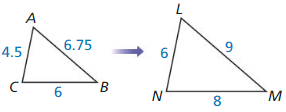
Answer:

Question 4.
DEFG ~ PQRS

Answer:

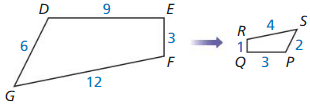
In Exercises 5-8, the polygons are similar. Find the value of x.

Question 5.

Answer:

Question 6.

Answer:
x = 20

Explanation:
\(\frac { DF }{ GJ } \) = \(\frac { DE }{ GH } \)
\(\frac { 16 }{ 12 } \) = \(\frac { x }{ 15 } \)
x = \(\frac { 16 x 15 }{ 12 } \) = \(\frac { 240 }{ 12 } \)
x = 20

Question 7.

Answer:

Question 8.

Answer:
x = 12

Explanation:
\(\frac { PN }{ KJ } \) = \(\frac { MN }{ JH } \)
\(\frac { x }{ 8 } \) = \(\frac { 9 }{ 6 } \)
x = \(\frac { 9 x 8 }{ 6 } \) = \(\frac { 72 }{ 6 } \)
x = 12

In Exercises 9 and 10, the black triangles are similar. Identify the type of segment shown in blue and find the value of the variab1e.

Question 9.

Answer:

Question 10.

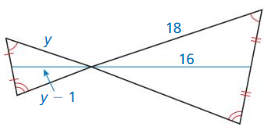
Answer:

Explanation:
\(\frac { y }{ 18 } \) = \(\frac { y – 1 }{ 16 } \)
18(y – 1) = 16y
18y – 18 = 16y
18y – 16y = 18
2y = 18
y = 9

In Exercises 11 and 12, RSTU ~ ABCD. Find the ratio of their perimeters.

Question 11.

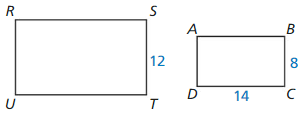
Answer:

Question 12.

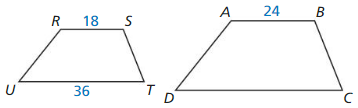
Answer:
\(\frac { RS + ST + TU + UR }{ AB + BC + CD + DA } \) = \(\frac { RS }{ AB } \) = \(\frac { 18 }{ 24 } \)
The ratio of perimeter is \(\frac { 3 }{ 4 } \).

In Exercises 13-16, two polygons are similar. The perimeter of one polygon and the ratio of the corresponding side lengths are given. Find the perimeter of the other polygon.

Question 13.
perimeter of smaller polygon: 48 cm: ratio: \(\frac{2}{3}\)
Answer:

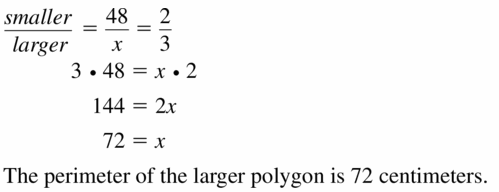
Question 14.
perimeter of smaller polygon: 66 ft: ratio: \(\frac{3}{4}\)

Answer:
The perimeter of larger polygon is 88 ft.

Explanation:
\(\frac { smaller }{ larger } \) = \(\frac { 66 }{ x } \) = \(\frac{3}{4}\)
66 x 4 = 3x
3x = 264
x = \(\frac { 264 }{ 3 } \) = 88

Question 15.
perimeter of larger polygon: 120 yd: rttio: \(\frac{1}{6}\)
Answer:

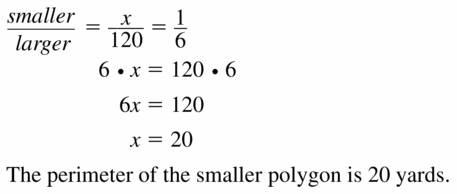
Question 16.
perimeter of larger polygon: 85 m; ratio: \(\frac{2}{5}\)

Answer:
The perimeter of smaller polygon is 34 m.

Explanation:
\(\frac { smaller }{ larger } \) = \(\frac { x }{ 85 } \) = \(\frac{2}{5}\)
85 x 2 = 5x
5x = 170
x = \(\frac { 170 }{ 5 } \) = 34

Question 17.
MODELING WITH MATHEMATICS
A school gymnasium is being remodeled. The basketball court will be similar to an NCAA basketball court, which has a length of 94 feet and a width of 50 feet. The school plans to make the width of the new court 45 feet. Find the perimeters of ail NCAA court and of the new court in the school.
Answer:

Question 18.
MODELING WITH MATHEMATICS
Your family has decided to put a rectangular patio in your backyard. similar to the shape of your backyard. Your backyard has a length of 45 feet and a width of 20 feet. The length of your new patio is 18 feet. Find the perimeters of your backyard and of the patio.

Answer:
The perimeter of the backyard is 130 ft.
Perimeter of patio is 52 ft

Explanation:
Draw a rectangle to represent the patio and a larger rectangle to represent our backyard and its going to similar figures

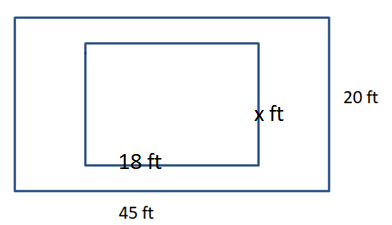
Perimeter of backyard = 2(45 + 20) = 2(65)
= 130 ft
Scale factor = \(\frac { 18 }{ 45 } \) = \(\frac { 2 }{ 5 } \)
So, \(\frac { perimeter of patio }{ perimeter of backyard } \) = \(\frac { 2 }{ 5 } \)
\(\frac { perimeter of patio }{ 130 } \) = \(\frac { 2 }{ 5 } \)
Perimeter of patio = \(\frac { 260 }{ 5 } \) = 52 ft

In Exercises 19-22, the polygons are similar. The area of one polygon is given. Find the area of the other polygon.

Question 19.

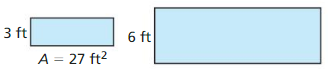
Answer:

Question 20.

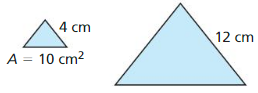
Answer:
Area of the larger triangle is 90 cm²

Explanation:
\(\frac { 10 }{ A } \) = (\(\frac { 4 }{ 12 } \))²
\(\frac { 10 }{ A } \) = \(\frac { 1 }{ 9 } \)
A = 10 x 9
A = 90

Question 21.

Answer:

Question 22.

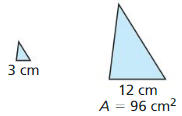
Answer:
Area of smaller triangle = 6 sq cm

Explanation:
\(\frac { A }{ 96 } \) = (\(\frac { 3 }{ 12 } \))²
\(\frac { A }{ 96 } \) = \(\frac { 1 }{ 16 } \)
16A = 96
A = \(\frac { 96 }{ 16 } \)
A = 6

Question 23.
ERROR ANALYSIS
Describe and correct the error in finding the perimeter of triangle B. The triangles are similar.

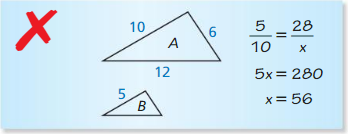
Answer:

Question 24.
ERROR ANALYSIS
Describe and correct the error in finding the area of triangle B. The triangles are similar.

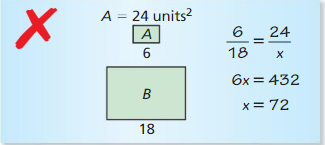
Answer:
Because the first ratio has a side of A over the side length of B, the square of the second ratio should have the area of B over the area of A.
\(\frac { 24 }{ x } \) = (\(\frac { 6 }{ 18 } \))²
\(\frac { 24 }{ x } \) = \(\frac { 1 }{ 9 } \)
x = 24 x 9
x = 216

In Exercises 25 and 26, decide whether the red and blue polygons are similar.

Question 25.

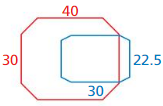
Answer:

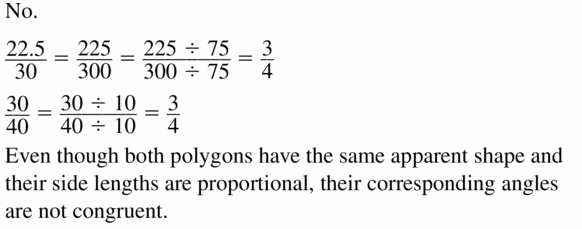
Question 26.

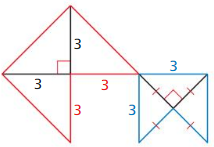
Answer:
Yes
Because both shapes are apparent and their side lengths are proportional and their corresponding angles are congruent.

Question 27.
REASONING
Triangles ABC and DEF are similar. Which statement is correct? Select all that apply.
(A) \(\frac{B C}{E F}=\frac{A C}{D F}\)
(B) \(\frac{A B}{D E}=\frac{C A}{F E}\)
(C) \(\frac{A B}{E F}=\frac{B C}{D E}\)
(D) \(\frac{C A}{F D}=\frac{B C}{E F}\)
Answer:

ANALYZING RELATIONSHIPS
In Exercises 28 – 34, JKLM ~ EFGH.

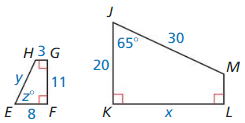
Question 28.
Find the scale factor of JKLM to EFGH.

Answer:
scale factor = \(\frac { EF }{ JK } \) =\(\frac { 8 }{ 20 } \)
k = \(\frac { 2 }{ 5 } \)

Question 29.
Find the scale factor of EFGH to JKLM.
Answer:

Question 30.
Find the values of x, y, and z.

Answer:
x = \(\frac { 55 }{ 2 } \)
y = 12
z = 65°

Explanation:
\(\frac { KL }{ GF } \) = \(\frac { x }{ 11 } \) = \(\frac { 5 }{ 2 } \)
2x = 55
x = \(\frac { 55 }{ 2 } \)
\(\frac { MJ }{ HE } \) = \(\frac { 30 }{ y } \) = \(\frac { 5 }{ 2 } \)
5y = 60
y = 12

Question 31.
Find the perimeter of each polygon.
Answer:

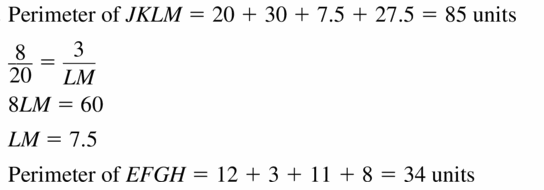
Question 32.
Find the ratio of the perimeters of JKLM to EFGH.

Answer:
The perimeter of JKLM : Perimeter of EFGH = 85 : 34

Question 33.
Find the area of each polygon.
Answer:

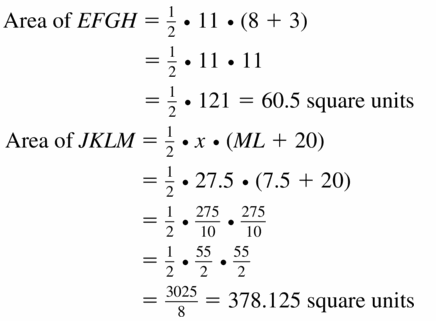
Question 34.
Find the ratio of the areas of JKLM to EFGH.

Answer:
Area of JKLM : Area of EFGH = 378.125 : 60.5 = 25 : 4

Question 35.
USING STRUCTURE
Rectangle A is similar to rectangle B. Rectangle A has side lengths of 6 and 12. Rectangle B has a side length of 18. What are the possible values for the length of the other side of rectangle B? Select all that apply.
(A) 6
(B) 9
(C) 24
(D) 36
Answer:

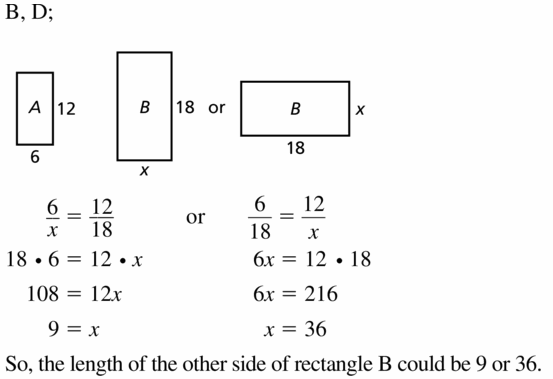
Question 36.
DRAWING CONCLUSIONS
In table tennis, the table is a rectangle 9 feet long and 5 feet wide. A tennis Court is a rectangle 78 feet long and 36 feet wide. Are the two surfaces similar? Explain. If so, find the scale factor of the tennis court to the table.

Answer:
The tennis table and court are not similar

Explanation:
If two figures are similar then their angles are congruent and sides are proportional.
If the tennis court and table are similar, then
\(\frac { length of table }{ length of court } \) = \(\frac { width of table }{ width of court } \)
\(\frac { 9 }{ 78 } \) = \(\frac { 5 }{ 36 } \)
9 • 36 = 5 • 78
324 = 390
So, Table and court are not similar.

MATHEMATICAL CONNECTIONS
In Exercises 37 and 38, the two polygons are similar. Find the values of x and y.

Question 37.

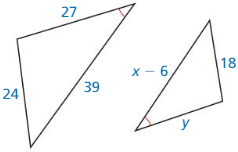
Answer:

Question 38.

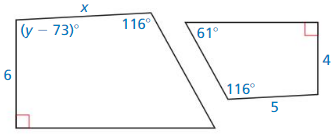
Answer:
x = 7.5

Explanation:
\(\frac { x }{ 5 } \) = \(\frac { 6 }{ 4 } \)
x = \(\frac { 15 }{ 2 } \)

ATTENDING TO PRECISION
In Exercises 39 – 42. the figures are similar. Find the missing corresponding side length.

Question 39.
Figure A has a pen meter of 72 meters and one of the side lengths is 18 meters. Figure B has a perimeter of 120 meters.
Answer:

Question 40.
Figure A has a perimeter of 24 inches. Figure B has a perimeter of 36 inches and one of the side lengths is 12 inches.

Answer:
The corresponding side length of figure A is 8 in

Explanation:
\(\frac { Perimeter of A }{ Perimeter of B } \) = \(\frac { Side length of A }{ Side length of B } \)
\(\frac { 24 }{ 36 } \) = \(\frac { x }{ 12 } \)
\(\frac { 2 }{ 3 } \) = \(\frac { x }{ 12 } \)
12 • 2 = 3x
x = 8

Question 41.
Figure A has an area of 48 square feet and one of the side lengths is 6 feet. Figure B has an area of 75 square feet.
Answer:

Question 42.
Figure A has an area of 18 square feet. Figure B has an area of 98 square feet and one of the side lengths is 14 feet.

Answer:
The corresponding side length of figure A is 6 ft.

Explanation:
\(\frac { Area of A }{ Area of B } \) = (\(\frac { Side length of A }{ Side length of B } \))²
\(\frac { 18 }{ 98 } \) = (\(\frac { x }{ 14 } \))²
\(\frac { 9 }{ 49 } \) = \(\frac { x² }{ 196 } \)
x² = 36
x = 6

CRITICAL THINKING
In Exercises 43-48, tell whether the polygons are always, sometimes, or never similar.

Question 43.
two isosceles triangles
Answer:

Question 44.
two isosceles trapezoids

Answer:
Two isosceles trapezoids are sometimes similar.

Question 45.
two rhombuses
Answer:

Question 46.
two squares

Answer:
Two squares are always similar.

Question 47.
two regular polygons
Answer:

Question 48.
a right triangle and an equilateral triangle

Answer:
A right triangle and an equilateral triangle are never similar.

Question 49.
MAKING AN ARGUMENT
Your sister claims that when the side lengths of two rectangles are proportional, the two rectangles must be similar. Is she correct? Explain your reasoning.
Answer:

Question 50.
HOW DO YOU SEE IT?
You shine a flashlight directly on an object to project its image onto a parallel screen. Will the object and the image be similar? Explain your reasoning.

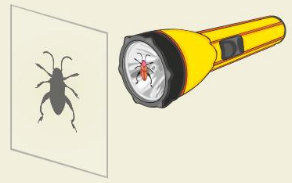
Answer:
The object and image are similar.

Question 51.
MODELING WITH MATHEMATICS
During a total eclipse of the Sun, the moon is directly in line with the Sun and blocks the Sun’s rays. The distance DA between Earth and the Sun is 93,00,000 miles. the distance DE between Earth and the moon is 2,40,000 miles, and the radius AB of the Sun is 432,5000 miles. Use the diagram and the given measurements to estimate the radius EC of the moon.

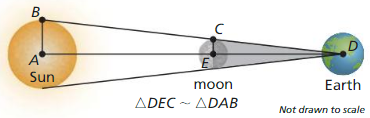
Answer:

Question 52.
PROVING A THEOREM
Prove the Perimeters of Similar Polygons Theorem (Theorem 8.1) for similar rectangles. Include a diagram in your proof.

Answer:

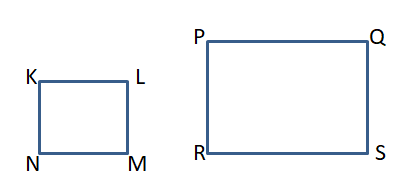
\(\frac { PQ + QR + RS + SP }{ KL + LM + MN + NK } \) = \(\frac { PQ }{ KL } \) = \(\frac { QR }{ LM } \) = \(\frac { RS }{ MN } \) = \(\frac { SP }{ NK } \)

Question 53.
PROVING A THEOREM
Prove the Areas of Similar Polygons Theorem (Theorem 8.2) for similar rectangles. Include a diagram in our proof.
Answer:

Question 54.
THOUGHT PROVOKING
The postulates and theorems in this book represent Euclidean geometry. In spherical geometry. all points are points on the surface of a sphere. A line is a circle on the sphere whose diameter is equal to the diameter of the sphere. A plane is the surface of the sphere. In spherical geometry, is it possible that two triangles are similar but not congruent? Explain your reasoning.
Answer:

• In Euclidean geometry, a postulate exists starting that through a point, there exists only one parallel line.
• In spherical geometry, great circles are straight lines and all of them intersect all the others. So, they are all parallel to each other. Thus, there are no parallel lines in spherical geometry.
• In spherical geometry, a line is a great circle. If there are many lines that contain any point then they are perpendicular to another line.
• So, in spherical geometry, eight right angles are formed by two perpendicular lines.

Question 55.
CRITICAL THINKING
In the diagram, PQRS is a square, and PLMS ~ LMRQ. Find the exact value of x. This value is called the golden ratio. Golden rectangles have their length and width in this ratio. Show that the similar rectangles in the diagram are golden rectangles.

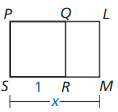
Answer:

Question 56.
MATHEMATICAL CONNECTIONS
The equations of the lines shown are y = \(\frac{4}{3}\)x + 4 and y = \(\frac{4}{3}\)x – 8. Show that ∆AOB ~ ∆COD.

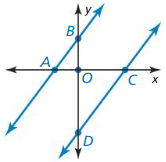
Answer:
The two lines slopes are equal and triangles angles are congruent and side lengths are proportional. So, triangles are similar.

Maintaining Mathematical proficiency

Find the value of x.

Question 57.

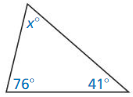
Answer:

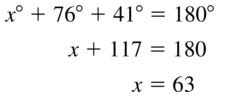
Question 58.

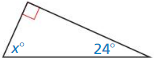
Answer:
x = 66°

Explanation:
x + 24 + 90 = 180
x + 114 = 180
x = 180 – 114
x = 66

Question 59.

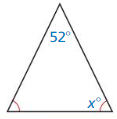
Answer:

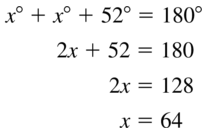
Question 60.

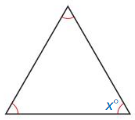
Answer:
x = 60°

Explanation:
x + x + x = 180
3x = 180
x = 60

8.2 Proving Triangle Similarity by AA

Exploration 1

Comparing Triangles

Work with a partner. Use dynamic geometry software.

a. Construct ∆ABC and ∆DEF So that m∠A = m∠D = 106°, m∠B = m∠E = 31°, and ∆DEF is not congruent to ∆ABC.

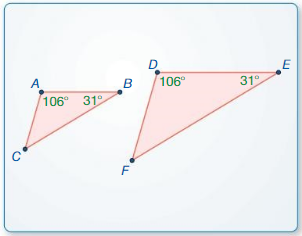
Answer:
m∠C ≠ m∠F

b. Find the third angle measure and the side lengths of each triangle. Copy the table below and record our results in column 1.

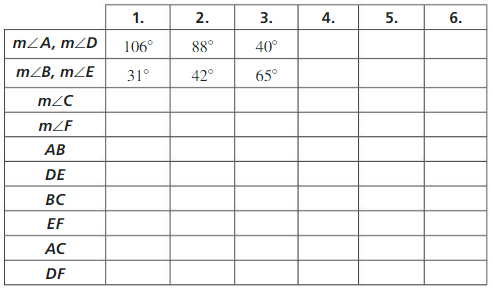
Answer:

c. Are the two triangles similar? Explain.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to understand and use stated assumptions, definitions, and previously established results in constructing arguments.
Answer:

d. Repeat parts (a) – (c) to complete columns 2 and 3 of the table for the given angle measures.
Answer:

e. Complete each remaining column of the table using your own choice of two pairs of equal corresponding angle measures. Can you construct two triangles in this way that are not similar?
Answer:

f. Make a conjecture about any two triangles with two pairs of congruent corresponding angles.
Answer:

Communicate Your Answer

Question 2.
What can you conclude about two triangles when you know that two pairs of corresponding angles are congruent?
Answer: If two pairs of corresponding angles in a pair of triangles are congruent, then the triangles are similar. Because if the two angle pairs are the same, then the third pair must also be equal when the three angle pairs are all equal, the three pairs of sides must be in proportion.

Question 3.
Find RS in the figure at the left.
Answer:
In a triangle RST
TS = RS
We know that TS = 4
Then
RS = 4.

Lesson 8.2 Proving Triangle Similarity by AA

Monitoring Progress

Show that the triangles are similar. Write a similarity statement.

Question 1.
∆FGH and ∆RQS

Answer:
∆FGH and ∆RQS are similar by the AA similarity theorem.

Question 2.
∆CDF and ∆DEF

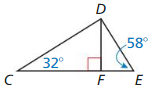
Answer:
m∠CDF + 32 = 90 degrees
m∠CDF = 58 degrees
∠CDF ≅∠DFE
And
∠CFE ≅ DFE
So, △CDF = △DEF.

Question 3.
WHAT IF?
Suppose that \(\overline{S R}\) \(\overline{T U}\) in Example 2 part (b). Could the triangles still be similar? Explain.
Answer:
You know∠SVR≅∠UVT by the vertical angles congruence theorem.
The diagram shows RS ∥UT
so∠S≡∠U by the Alternate Interior Angles Theorem.
So,△SVR∼△UVT by the AA similarity postulate.
If,SR ∦ TU it breaks the AA singularity postulate.
So,△SVR≠△UVT.

Question 4.
WHAT IF?
A child who is 58 inches tall is standing next to the woman in Example 3. How long is the child’s shadow’?
Answer:
Given that,
The child is 58 inches tall and is standing next to the woman.
The child shadow is 60/58 = 40/x
2330 = 60x
2330/60 = x
x = 38.8.
Therefore Childs shadow is 38.8 cm.

Question 5.
You are standing outside, and you measure the lengths 0f the shadows cast by both you and a tree. Write a proportion showing how you could find the height of the tree.
Answer:
The propagation shows to find the height of the tree is
My height/tree height = my shadow/tree shadow.

Exercise 8.2 Proving Triangle Similarity by AA

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
If two angles of one triangle are congruent to two angles of another triangle. then the triangles are __________ .
Answer:

Question 2.
WRITING
Can you assume that corresponding sides and corresponding angles of any two similar triangles are congruent? Explain.
Answer: The corresponding angles of two similar triangles are always congruent but the corresponding angles of two analogous triangles are always harmonious but the corresponding sides of the two triangles don’t have to be harmonious. In an analogous triangle, the corresponding sides are commensurable which means that the rates of corresponding sides are equal. However, also the corresponding sides are harmonious, but in other cases, if these rates are 1.

Monitoring Progress and Modeling with Mathematics

In Exercises 3 – 6. determine whether the triangles are similar. If they are, write a similarity statement. Explain your reasoning.

Question 3.

Answer:

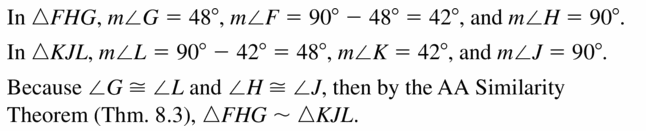
Question 4.

Answer:
Sum of all the angles of a triangle = 180°
m∠R + m∠Q + m∠S = 180
m∠R + 85 + 35 = 180
m∠R = 180 – 120
m∠R = 60
In triangle VUT,
m∠V + m∠U + m∠T = 180
m∠V + 65 + 35 = 180
m∠V + 100 = 180
m∠V = 180 – 100
m∠V = 80
In triangle RQS
m∠R = 60, m∠Q = 85, m∠S = 35
In VUT,
m∠V = 80, m∠U = 65, m∠T = 35

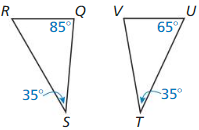
Question 5.

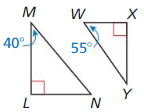
Answer:

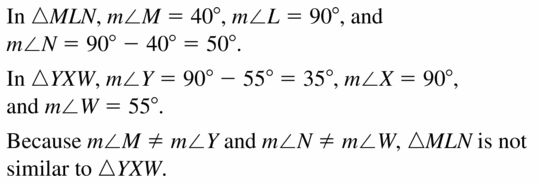
Question 6.

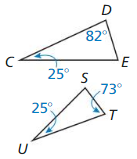
Answer:
Sum of all the angles of a triangle = 180°
In triangle CDE,
m∠D + m∠C + m∠E = 180
82 + 25 + m∠E = 180
107 + m∠E = 180
m∠E = 180 – 107
m∠E = 73
In triangle STU
m∠S + m∠U + m∠T = 180
m∠S + 25 + 73 = 180
m∠S + 98 = 180
m∠S = 180 – 98
m∠S = 82

In Exercises 7 – 10. show that the two triangles are similar.

Question 7.

Answer:

Question 8.

Answer:
From the given figure LQ ∥MP
Therefore, by the corresponding angle theorem,
∠LQN=∠MPN
Now, inΔLQN and ΔMNP
​∠LNQ=∠MNP​ and
∠LQN=∠MPN
Therefore, Two pairs of angles are congruent.
So, ΔLQN ≈ ΔMPN by the AA similarity theorem.

Question 9.

Answer:

Question 10.

Answer:
It is required to show that the two triangles △RUT and △RSV are similar.
To show that the two triangles are similar, use Angle-Angle (AA) Similarity Theorem.
Since RT∥SV, ∠TRU ≅ ∠SVR by the Alternate Interior Angles Theorem.
List the pairs of congruent angles in △RUT
and △RSV
​∠RUT≅∠RSV
∠TRU≅∠SVR
So, by the Angle-Angle Similarity Theorem, △RUT∼△RSV

In Exercises 11 – 18, use the diagram to copy and complete the statement.

Question 11.
∆CAG ~ _________
Answer:

Question 12.
∆DCF ~ _________
Answer: △DCF ~ △BCG

Question 13.
∆ACB ~ _________
Answer:

Question 14.
m∠ECF = _________
Answer: m∠ECF = 37 degrees.

Question 15.
m∠ECD = _________
Answer:

Question 16.
CF = _________
Answer: CF = 16

Question 17.
BC = _________
Answer:

Question 18.
DE = _________
Answer: DE = 21

Question 19.
ERROR ANALYSIS
Describe and correct the error in using the AA Similarity Theorem (Theorem 8.3).

Answer:

Question 20.
ERROR ANALYSIS
Describe and correct the error in finding the value of x.

Answer:
First divide the diagram into two triangles.

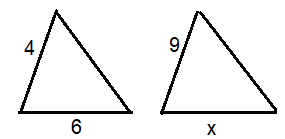
4/9 = 6/x
4x = 54
x = 54/4
x = 27/2
x = 13.5

Question 21.
MODELING WITH MATHEMATICS
You can measure the width of the lake using a surveying technique, as shown in the diagram. Find the width of the lake, WX. Justify your answer.

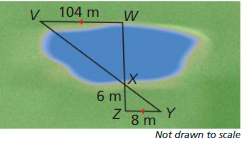
Answer:

Question 22.
MAKING AN ARGUMENT
You and your cousin are trying to determine the height of a telephone pole. Your cousin tells you to stand in the pole’s shadow so that the tip of your shadow coincides with the tip of the pole’s shadow. Your Cousin claims to be able to use the distance between the tips of the shadows and you, the distance between you and the pole, and your height to estimate the height of the telephone pole. Is this possible? Explain. Include a diagram in your answer.
Answer:

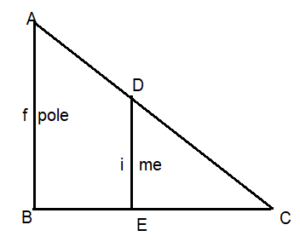
To estimate the height of the pole △CDE can be proved similar to △CAD as
∠C (common angle)

∠CED = ∠CBA (corresponding angles)

If two angles of one triangle are congruent to two angles of another triangle, then the two triangles are similar.
△CDE ~ △CAB

Corresponding angles are congruent and corresponding sides are proportional for similar triangles.
DE/AB = CE/CB is an equation 1
Measure my height (DE), shadows CE and CB to calculate the height of pole (AB) from equation 1.

REASONING
In Exercises 23 – 26, is it possible for ∆JKL and ∆XYZ to be similar? Explain your reasoning.

Question 23.
m∠J = 71°, m∠K = 52°, m∠X = 71°, and m∠Z = 57°
Answer:

Question 24.
∆JKL is a right triangle and m∠X + m∠Y= 150°.
Answer:
The sum of angles = 180
150 + 90 > 180
So, the answer is no.

Question 25.
m∠L = 87° and m∠Y = 94°
Answer:

Question 26.
m∠J + m∠K = 85° and m∠Y + m∠Z = 80°
Answer:
The third angle in both triangles would be:
For△JKL
​m∠L=180−85
m∠L=95
For△XYZ,
​m∠X=180 − 80
m∠X=100
So, there wouldn’t be any single similar angle.
So, no the two triangles△JKL,△ XYZ could not be similar.

Question 27.
MATHEMATICAL CONNECTIONS
Explain how you can use similar triangles to show that any two points on a line can be used to find its slope.

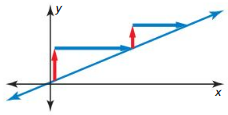
Answer:

Question 28.
HOW DO YOU SEE IT?
In the diagram, which triangles would you use to find the distance x between the shoreline and the buoy? Explain your reasoning.

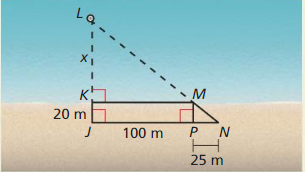
Answer:
(x + 20)/20 = 125/25
x + 20 = 20 × 5
x + 20 = 100
x = 100 – 20
x = 80 meters

Question 29.
WRITING
Explain why all equilateral triangles are similar.
Answer:

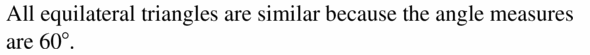
Question 30.
THOUGHT PROVOKING
Decide whether each is a valid method of showing that two quadrilaterals are similar. Justify your answer.
a. AAA
Answer: The AAA Similarity Theorem is for triangles only and therefore, cannot be applied in case of quadrilaterals. Hence the AAA system is not valid for showing two quadrilaterals to be analogous.

b. AAAA
Answer: The AAAA method is not a valid method for showing two quadrilaterals to be similar as in case of the rectangle and a square, all the four and the rectangle are not similar because the corresponding sides are not proportional.

Question 31.
PROOF
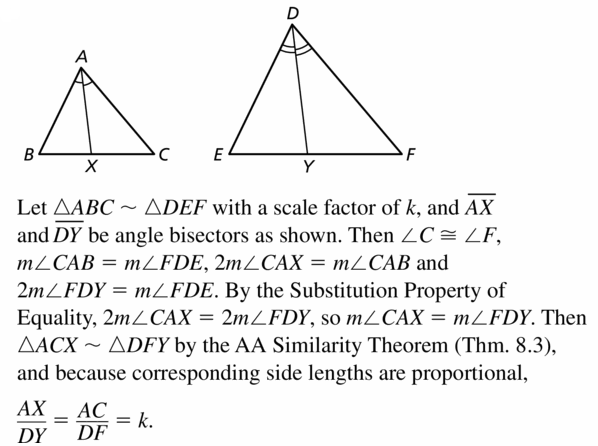
Without using corresponding lengths in similar polygons. prove that the ratio of two corresponding angle bisectors in similar triangles is equal to the scale factor.
Answer:

Question 32.
PROOF
Prove that if the lengths of two sides of a triangle are a and b, respectively, then the lengths of the corresponding altitudes to those sides are in the ratio \(\frac{b}{a}\).
Answer:
Let a triangle △ABC be given and let its sides be BC = a, AC = b.
Let AM and BN are altitudes of corresponding sides of triangles △ABC
We know that the altitude of a triangle is the perpendicular drawn from the vertex of the triangle to the opposite side.
The two right triangles are △AMC and △BNC.
We can conclude that the pairs of congruent angles are
∠AMC ≅∠BNC ≅ 90 degrees.
∠ACM ≅∠BCN
△AMC ~ △BCN by the angle – angle similarity theorem.
The triangles are similar and therefore their corresponding angles are congruent.
AM/BN = AC/BC = b/a.

Question 33.
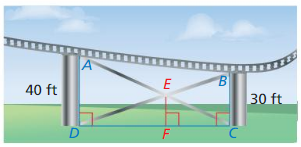
MODELING WITH MATHEMATICS
A portion of an amusement park ride is shown. Find EF. Justify your answer.

Answer:

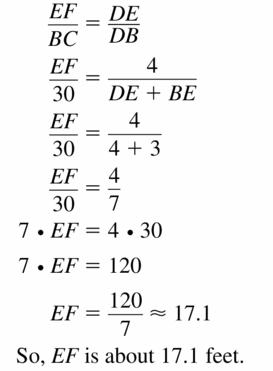
Maintaining Mathematical Practices

Determine whether there is enough information to prove that the triangles are congruent. Explain your reasoning.

Question 34.

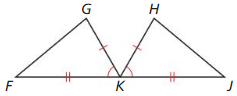
Answer: By the SAS Theorem △EFK ≅ HJK.

Question 35.

Answer:

Question 36.

Answer: By the SAS theorem ∠QSP ≅∠QSR

8.1 & 8.2 Quiz

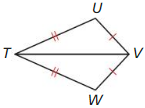
List all pairs of congruent angles. Then write the ratios of the corresponding side lengths in a statement of proportionality.

Question 1.
∆BDG ~ ∆MPQ

Answer:
The congruent angles are
m∠BDG = m∠MPQ
m∠DBG = m∠PMQ
m∠DGB = m∠PQM
The ratios of its corresponding sides is equal to
BD/MP = DG/PQ = BG/MQ.

Question 2.
DEFG ~ HJKL

Answer:
All the pairs of congruent angles
∠GFE = ∠HJK
The ratios of the corresponding side lengths
FE/JK = ED/KL
ED/KL = DG/LH
DG/LH = GF/HJ

The polygons are similar. Find the value of x.

Question 3.

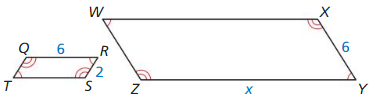
Answer:
Given that the polygons are similar.
From the given data
RS/XY = QR/YZ
2/x = 6/6
2/x = 1
2 = x
Therefore the value of x is 2.

Question 4.

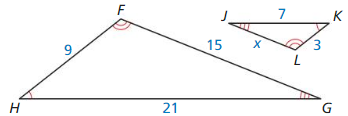
Answer:
FG/JL = HG/JK
15/x = 21/7
15/x = 3
15/3 = x
x = 5

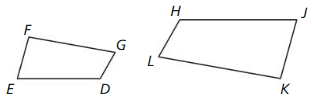
Determine whether the polygons are similar. If they are, write a similarity statement. Explain your reasoning. (Section 8.1 and Section 8.2)

Question 5.

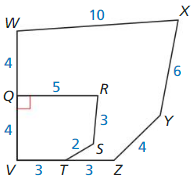
Answer:
QR/WR = 5/10 = 1/2
RS/XY = 3/6 = 1/2
ST/YZ = 2/4 = 1/2
TV/ZV = 3/(ZT + TV) = 3/(3+3) = 3/6 = 1/2
VQ/VW = 4/(VQ + QW) = 4/(4+4) = 4/8 = 1/2
But not all the corresponding angles are congruent.
The polygons are not similar.

Question 6.

Answer:
In ΔJKH
∠K = 180 – (37 + 90)
∠K = 180 – 127 = 53
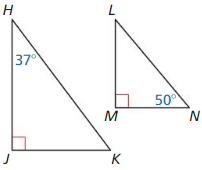
In ΔMNL
∠L = 180 – (90 + 50)
∠L = 180 – 140
∠L = 40
Since here two triangles dont have congruent
Thus they are not similar.

Question 7.

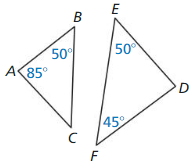
Answer:
∠B = ∠E = 50
∠A = 85
∠C = x
∠F = 45
∠D = y
The angles of both the triangles are similar but not congruent because the angles are not the same.

Show that the two triangles are similar.

Question 8.

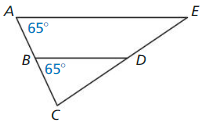
Answer:
The triangles that have the same shape but a different size is known as similar.
ΔBCD and ΔACE are similar triangles.

Question 9.

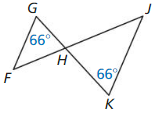
Answer:
The triangles that have the same shape but a different size is known as similar.
ΔFGH and ΔHJK are similar triangles.

Question 10.

Answer:
The triangles that have the same shape but a different size is known as similar.
ΔEFG and ΔDFH are similar triangles.

Question 11.
The dimensions of an official hockey rink used by the National Hockey League (NHL) are 200 feet by 85 feet. The dimensions of an air hockey table are 96 inches by 408 inches. Assume corresponding angles are congruent. (Section 8.1)
a. Determine whether the two surfaces are similar.
Answer:
Given,
The dimensions of an official hockey rink used by the National Hockey League (NHL) are 200 feet by 85 feet. The dimensions of an air hockey table are 96 inches by 408 inches.
1 feet = 12 inches
200 feet = 200 × 12 = 2400 inches
85 feet = 85 × 12 = 1020 inches
Dimensions of a hockey rink in inches are 2400 inches by 1020 inches
If the measure of the corresponding sides that include the angles are proportional hockey rink and hockey table are similar
200/96 = 240/96 = 25 inches
85/40.8 = 1020/10.8 = 25 inches
2400/96 = 1020/40.8 = 25 inches
Thus the two rinks are similar.

b. If the surfaces are similar, find the ratio of their perimeters and the ratio of their areas. If not, find the dimensions of an air hockey table that are similar to an NHL hockey rink.
Answer:
P1 = 2(l + w)
2(2400 + 1020)
2(3420) = 6840 inches
P2 = 2(l + w)
2(96 + 40.8)
2(136.8)
= 273.6 inches
P1/P2 = 6840/273.6 = 25 inches
A1 = lw
A1 = 2400 × 1020 = 2448000 sq. inch
A2 = lw
A2 = 96 × 40.8
= 3916.8 sq. inch
A1/A2 = 2448000/3916.8 = 625 sq. inch

Question 12.
you and a friend buy camping tents made by the same company but in different sizes and colors. Use the information given in the diagram to decide whether the triangular faces of the tents are similar. Explain your reasoning. (Section 8.2)

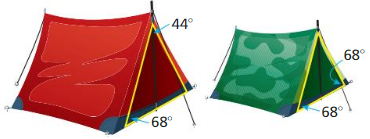
Answer:
x1 = 68 degrees
y 1= 44 degrees
∠z1 = 180 – (68 + 44)
∠z1 = 180 – 112 = 68 degrees
x2 = 68
y2 = 68
∠z2 = 180 – (68 + 68)
= 180 – 136 = 44 degrees
By AAA theorem, the red and green tents are similar.
Thus my friend’s tents and my tents are similar.

8.3 Proving Triangle Similarity by SSS and SAS

Exploration 1

Deciding Whether Triangles Are Similar

Work with a partner: Use dynamic geometry software.

a. Construct ∆ABC and ∆DEF with the side lengths given in column 1 of the table below.

Answer:

b. Copy the table and complete column 1.
Answer:

c. Are the triangles similar? Explain your reasoning.
Answer:

d. Repeat parts (a) – (c) for columns 2 – 6 in the table.
Answer:

e. How are the corresponding side lengths related in each pair of triangles that are similar? Is this true for each pair of triangles that are not similar?
Answer:

f. Make a conjecture about the similarity of two triangles based on their corresponding side lengths.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to analyze situations by breaking them into cases and recognize and use counterexamples.
Answer:

g. Use your conjecture to write another set of side lengths of two similar triangles. Use the side lengths to complete column 7 of the table.
Answer:

Exploration 2

Deciding Whether Triangles Are Similar

Work with a partner: Use dynamic geometry software. Construct any ∆ABC.
a. Find AB, AC, and m∠A. Choose any positive rational number k and construct ∆DEF so that DE = k • AB, DF = k • AC, and m∠D = m∠A.
Answer:

b. Is ∆DEF similar to ∆ABC? Explain your reasoning.
Answer:

c. Repeat parts (a) and (b) several times by changing ∆ABC and k. Describe your results.
Answer:

Communicate Your Answer

Question 3.
What are two ways to use the corresponding sides of two triangles to determine that the triangles are similar?
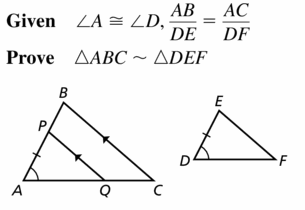
Answer: If the pairs of corresponding sides are in proportion and the included angle of each pair is equal. Then the two triangles they form are similar. Any time two sides of a triangle and their included angles are fixed. Then all three vertices of that triangle are fixed.

Lesson 8.3 Proving Triangle Similarity by SSS and SAS

Monitoring progress

Use the diagram.

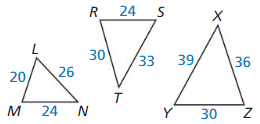
Question 1.
Which of the three triangles are similar? Write a similarity statement.

Answer:
The ratios are equal. So, △LMN, △XYZ are similar.
The ratios are not equal. So △LMN, △RST are not similar.

Explanation:
Compare △LMN, △XYZ by finding the ratios of corresponding side lengths
Shortest sides: \(\frac { LM }{ YZ } \) = \(\frac { 20 }{ 30 } \) = \(\frac { 2 }{ 3 } \)
Longest sides: \(\frac { LN }{ XY } \) = \(\frac { 26 }{ 39 } \) = \(\frac { 2 }{ 3 } \)
Remaining sides: \(\frac { MN }{ ZX } \) = \(\frac { 24 }{ 36 } \) = \(\frac { 2 }{ 3 } \)
The ratios are equal. So, △LMN, △XYZ are similar.
Compare △LMN, △RST by finding the ratios of corresponding side lengths
Shortest sides: \(\frac { LM }{ RS } \) = \(\frac { 20 }{ 24 } \) = \(\frac { 5 }{ 6 } \)
Longest sides: \(\frac { LN }{ ST } \) = \(\frac { 26 }{ 33 } \)
Remaining sides: \(\frac { MN }{ RT } \) = \(\frac { 24 }{ 30 } \) = \(\frac { 4 }{ 5 } \)
The ratios are not equal. So △LMN, △RST are not similar.

Question 2.
The shortest side of a triangle similar to ∆RST is 12 units long. Find the other side 1enths of the triangle.

Answer:
The other side lengths of the triangle are 15 units, 16.5 units.

Explanation:
The shortest side of a triangle similar to ∆RST is 12 units
Scale factor = \(\frac { 12 }{ 24 } \) = \(\frac { 1 }{ 2 } \)
So, other sides are 33 x \(\frac { 12 }{ 2 } \) = 16.5, 30 x \(\frac { 12 }{ 2 } \) = 15.

Explain how to show that the indicated triangles are similar.

Question 3.
∆SRT ~ ∆PNQ

Answer:
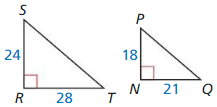
The shorter sides: \(\frac { 18 }{ 24 } \) = \(\frac { 3 }{ 4 } \)
Longer sides: \(\frac { 21 }{ 28 } \) = \(\frac { 3 }{ 4 } \)
The side lengths are proportional. So ∆SRT ~ ∆PNQ

Question 4.
∆XZW ~ ∆YZX

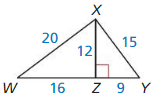
Answer:
∆XZW and ∆YZX are not proportional.

Explanation:
The shorter sides: \(\frac { 9 }{ 16 } \)
Longer sides: \(\frac { 15 }{ 20 } \) = \(\frac { 3 }{ 4 } \)
The side lengths are not proportional. So ∆XZW and ∆YZX are not proportional.

Exercise 8.3 Proving Triangle Similarity by SSS and SAS

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE SENTENCE
You plan to show that ∆QRS is similar to ∆XYZ by the SSS Similarity Theorem (Theorem 8.4). Copy and complete the proportion that you will use:

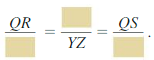
Answer:

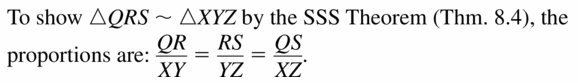
Question 2.
WHICH ONE DOESN’T BELONG?
Which triangle does not belong with the other three? Explain your reasoning.

Answer:
Among the four triangles the second triangle is different.
The second triangle is not a right-angled triangle.
Except for the second triangle all triangles are right angled triangles.

Monitoring progress and Modeling with Mathematics

In Exercises 3 and 4, determine whether ∆JKL or ∆RST is similar to ∆ABC.

Question 3.

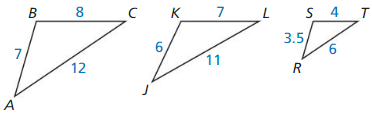
Answer:

Question 4.

Answer:
Compare the corresponding sides of ∆ABC and ∆JKL
14/17.5 = 0.8 shortest sides
16/20 = 0.8 longest sides
20/25 = 0.8 remaining sides
All the ratios of corresponding length sides is equal, it is called the scale factor and it is equal to 0.8
∆ABC ∼ ∆JKL by the SSS similarity theorem
14/10.5 ≈ 1.33 shortest sides
16/12 ≈ 1.33 longest sides
20/16 = 1.25 remaining sides
The ratio of corresponding length sides are not equal.
So, ∆ABC is not similar to ∆JKL

In Exercises 5 and 6, find the value of x that makes ∆DEF ~ ∆XYZ.

Question 5.

Answer:

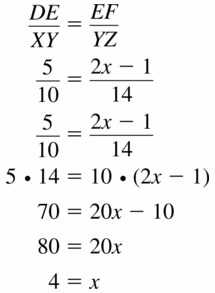
Question 6.

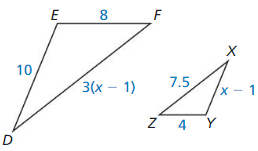
Answer:
3(x -1)/7.5 = 8/4
(3x – 3) × 4 = 8 × 7.5
12x – 12 = 60
12x = 60 + 12
12x = 72
x = 72/12
x = 6

In Exercises 7 and 8, verify that ∆ABC ~ ∆DEF Find the scale factor of ∆ABC to ∆DEF

Question 7.
∆ABC: BC = 18, AB = 15, AC = 12
∆DEF: EF = 12, DE = 10, DF = 8
Answer:

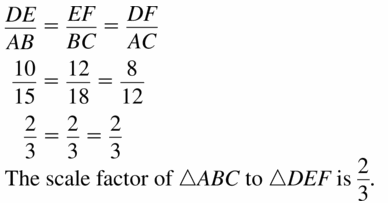
Question 8.
∆ABC: AB = 10, BC = 16, CA = 20
∆DEF: DE = 25, EF = 40, FD =50
Answer:
Compare △ABC and △DEF
DE/AB = 25/10 = 5/2
EF/BC = 40/16 = 5/2
FD/CA = 50/20 = 5/2
All the ratios of corresponding length sides are equal. It is called a scale factor and its length is equal to 5/2.
So, △ABC ~△DEF by the SSS similarity theorem.

In Exercises 9 and 10. determine whether the two triangles are similar. If they are similar, write a similarity statement and find the scale factor of triangle B to triangle A.

Question 9.

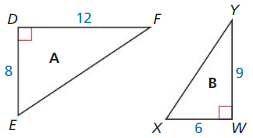
Answer:

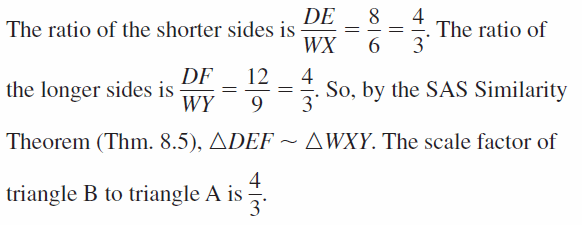
Question 10.

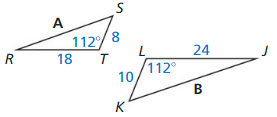
Answer:
Use SAS similarity theorem to check the similarity of triangles
∠T = ∠L
ST/KL = 8/10 = 4/5
RT/JL = 18/24 = 3/4
Here the lengths of the sides that include ∠T and ∠L are not proportional
Since the triangles are not similar, thus the scale factor cannot be found.
Hence the scale factor does not similar in this case.

In Exercises 11 and 12, sketch the triangles using the given description. Then determine whether the two triangles can be similar.

Question 11.
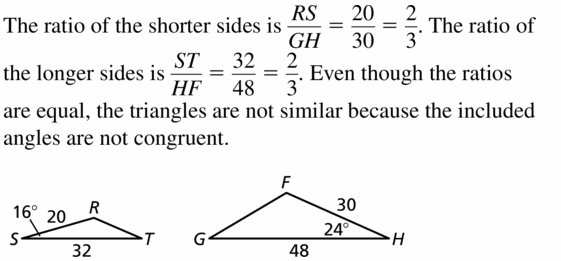
In ∆RST, RS = 20, ST = 32, and m∠S = 16°. In ∆FGH, GH = 30, HF = 48, and m∠H = 24°.
Answer:

Question 12.
The side lengths of ∆ABC are 24, 8x, and 48, and the side lengths of ∆DEF are 15, 25, and 6x.

Answer:
\(\frac { AB }{ DE } \) = \(\frac { AC }{ DF } \) = \(\frac { BC }{ EF } \)
\(\frac { 24 }{ 15 } \) = \(\frac { 8x }{ 25 } \)
x = 5

In Exercises 13 – 16. show that the triangles are similar and write a similarity statement. Explain your reasoning.

Question 13.

Answer:

Question 14.

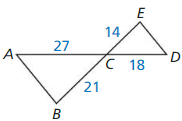
Answer:
ACB ∼ DCE
CD/AB = 18/27
CD/AB = 2/3
EC/BC = 14/21
EC/BC = 2/3
∠ACB = ∠CED

Question 15.

Answer:

Question 16.

Answer:
In ∆SRQ
SR = 12
RQ = 16
QS = 24
SR/VU = 12/9 = 4/3
QS/TV = 24/18 = 4/3
RQ/UT = 16/12 = 4/3
All the ratios of the corresponding sides of ∆SRQ and ∆VUT are equal.
Therefore, by SSS similarity theorem ∆SRQ ∼ ∆VUT.
The ratio of the corresponding shortest sides, longest sides and remaining sides are equal which satisfies the condition of SSS similarity theorem.
Thus by SSS similarity condition, the given triangles are similar.

In Exercises 17 and 18, use ∆XYZ.

Question 17.
The shortest side of a triangle similar to ∆XYZ is 20 units long. Find the other side lengths of the triangle.
Answer:

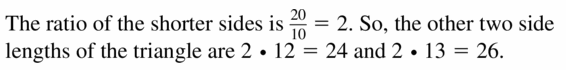
Question 18.
The longest side of a triangle similar to ∆XYZ is 39 units long. Find the other side lengths of the triangle.
Answer:
The longest side of a triangle similar to ∆XYZ is 39 units long.
13/39 = 12/y
13y = 39 × 12
13y = 468
y = 468/13
y = 36
13/39 = 10/y
13y = 39(10)
13y = 390
y = 390/13
y = 30
The side lengths are 30, 36 and 39.

Question 19.
ERROR ANALYSIS
Describe and correct the error in writing a similarity statement.

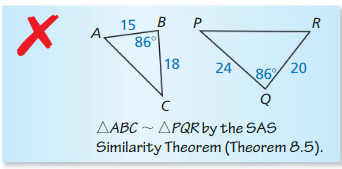
Answer:

Question 20.
MATHEMATICAL CONNECTIONS
Find the value of n that makes ∆DEF ~ ∆XYZ when DE = 4, EF = 5, XY = 4(n + 1), YZ = 7n – 1, and ∠E ≅ ∠Y. Include a sketch.

Answer:
\(\frac { DE }{ XY } \) = \(\frac { EF }{ YZ } \)
\(\frac { 4 }{ 4(n + 1) } \) = \(\frac { 5 }{ 7n – 1 } \)
cross multiply the fractions
4(7n – 1) = 20(n + 1)
28n – 4 = 20n + 20
28n – 20n = 20 + 4
8n = 24
n = \(\frac { 24 }{ 8 } \)
n = 3

ATTENDING TO PRECISION
In Exercises 21 – 26, use the diagram to copy and complete the statement.

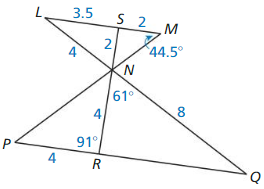
Question 21.
m∠LNS = ___________
Answer:

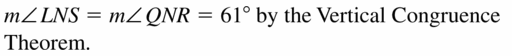
Question 22.
m∠NRQ = ___________
Answer:
m∠NRQ = m∠NRP = 91° by the vertical congruence

Question 23.
m∠NQR = ___________
Answer:

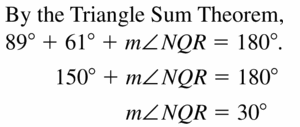
Question 24.
RQ = ___________

Answer:
RQ = 4√3

Explanation:
Using the pythogrean theorem
NQ² = NR² + RQ²
8² = 4² + RQ²
64 = 16 + RQ²
64 – 16 = RQ²
48 = RQ²
RQ = 4√3

Question 25.
m∠NSM = ___________
Answer:

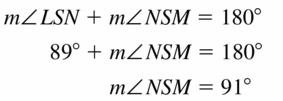
Question 26.
m∠NPR = ___________

Answer:
m∠NPR = 28°

Explanation:
m∠NPR + m∠NRP + m∠RNP = 180°
m∠NPR + 91° + 61° = 180°
m∠NPR + 152° = 180°
m∠NPR = 180° – 152°
m∠NPR = 28°

Question 27.
MAKING AN ARGUMENT
Your friend claims that ∆JKL ~ ∆MNO by the SAS Similarity Theorem (Theorem 8.5) when JK = 18, m∠K = 130° KL = 16, MN = 9, m∠N = 65°, and NO = 8, Do you support your friend’s claim? Explain your reasoning.
Answer:

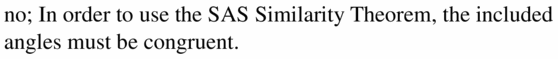
Question 28.
ANALYZING RELATIONSHIPS
Certain sections of stained glass are sold in triangular, beveled pieces. Which of the three beveled pieces, if any, are similar?

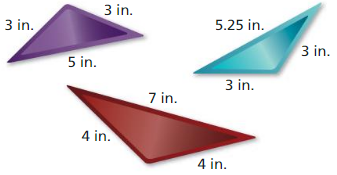
Answer:
Out of three triangles, violet and blue triangles are similar.

Explanation:
Check the similarity of maroon and violet triangles.
longest sides: \(\frac { 5 }{ 7 } \)
shortest sides: \(\frac { 3 }{ 4 } \)
remaining sides: \(\frac { 3 }{ 4 } \)
The ratios are not equal. So those traingles are not similar.
Check the similarity of blue and violet triangles.
longest sides: \(\frac { 5 }{ 5.25 } \) = 1
shortest sides: \(\frac { 3 }{ 3 } \) = 1
remaining sides: \(\frac { 3 }{ 3 } \) = 1
The ratios are equal. So those traingles are similar.

Question 29.
ATTENDING TO PRECISION
In the diagram, \(\frac{M N}{M R}=\frac{M P}{M Q}\) Which of the statements must be true?
Select all that apply. Explain your reasoning.

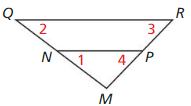
(A) ∠1 ≅∠2
(B) \(\overline{Q R}\) || \(\overline{N P}\)
(C)∠1 ≅ ∠4
(D) ∆MNP ~ ∆MRQ
Answer:

Question 30.
WRITING
Are any two right triangles similar? Explain.

Answer:
Yes, any two right triangles can be similar. If two right triangles are similar, then the ratio of their longest, smallest and remaining side lengths must be equal and their angles must be congruent.

Question 31.
MODELING WITH MATHEMATICS
In the portion of the shuffleboard court shown, \(\frac{B C}{A C}=\frac{B D}{A E}\)

a. What additional information do you need to show that ∆BED ~ ∆ACE using the SSS Similarity Theorem (Theorem 8.4)?
b. What additional information do, you need to show that ∆BCD ~ ∆ACE using the SAS Similarity Theorem (Theorem 8.5)?
Answer:

Question 32.
PROOF
Given that ∆BAC is a right triangle and D, E, and F are midpoints. prove that m∠DEF = 90°.

Answer:
By observing the triangle ABC, m∠BAC = 90°
Join the midpoints of the sides of the triangle.
m∠DEF = 90°

Question 33.
PROVING A THEOREM
Write a two-column proof of the SAS Similarity Theorem (Theorem 8.5).
Given ∠A ≅ ∠D, \(\frac{A B}{D E}=\frac{A C}{D F}\)
Prove ∆ABC ~ ∆DEF

Answer:

Question 34.
CRITICAL THINKING
You are given two right triangles with one pair of corresponding legs and the pair of hypotenuses having the same length ratios.
a. The lengths of the given pair of corresponding legs are 6 and 18, and the lengths of the hypotenuses are 10 and 30. Use the Pythagorean Theorem to find the lengths of the other pair of corresponding legs. Draw a diagram.
Answer:

b. Write the ratio of the lengths of the second pair of corresponding legs.
Answer:
First find the length of AC using pythagorean theorem
AC² + AB² = BC²
AC² + 36 = 100
AC² = 64
AC = 8
Find the length of DF using pythagorean theorem
DF² + DE² = EF²
DF² + 18² = 30²
DF² = 900 – 324
DF² = 576
DF= 24

c. Are these triangles similar? Does this suggest a Hypotenuse-Leg Similarity Theorem for right triangles? Explain.
Answer:
k = \(\frac { AC }{ DF } \) = \(\frac { 8 }{ 24 } \) = \(\frac { 1 }{ 3 } \)
k = \(\frac { AB }{ DE } \) = \(\frac { 6 }{ 18 } \) = \(\frac { 1 }{ 3 } \)
So, triangles are similar.

Question 35.
WRITING
Can two triangles have all three ratios of corresponding angle measures equal to a value greater than 1 ? less than 1 ? Explain.
Answer:

Question 36.
HOW DO YOU SEE IT?
Which theorem could you use to show that ∆OPQ ~ ∆OMN in the portion of the Ferris wheel shown when PM = QN = 5 feet and MO = NO = 10 feet?

Answer:
The corresponding angle theorem states that ∆OPQ is similar to ∆OMN.

Question 37.
DRAWING CONCLUSIONS
Explain why it is not necessary to have an Angle-Side-Angle Similarity Theorem.
Answer:

Question 38.
THOUGHT PROVOKING
Decide whether each is a valid method of showing that two quadrilaterals are similar. Justify your answer.
a. SASA
Answer:
If an angle of one triangle is congruent to an angle of a second triangle and the lengths of the sides including these angles are proportional, then the triangles are similar.

b. SASAS
Answer:
If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle, the triangles are congruent.

c. SSSS
Answer:
If the corresponding side lengths of two triangles are proportional, then the triangles are similar.

d. SASSS
Answer:
If two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then those two triangles are similar.

Question 39.
MULTIPLE REPRESENTATIONS
Use a diagram to show why there is no Side-Side-Angle Similarity Theorem.
Answer:

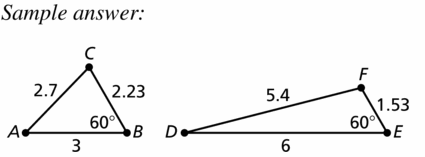
Question 40.
MODELING WITH MATHEMATICS
The dimensions of an actual swing set are shown. You want to create a scale model of the swing set for a dollhouse using similar triangles. Sketch a drawing of your swing set and label each side length. Write a similarity statement for each pair of similar triangles. State the scale factor you used to create the scale model.

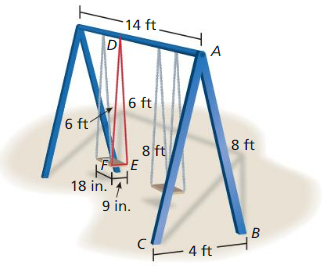
Answer:
Here we have to check the similarity statement for △ABC, △DEF.
The scale factor k = \(\frac { AB }{ DE } \) = \(\frac { 8 }{ 6 } \) = \(\frac { 4 }{ 3 } \)

Question 41.
PROVING A THEOREM
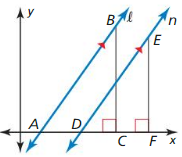
Copy and complete the paragraph proot of the second part of the Slopes of Parallel Lines Theorem (Theorern 3. 13) from page 439.
Given m_l = m_n, l and n are nonvertical.
Prove l || n
You are given that m_l = m_n. By the definition of slope. m_l = \(\frac{B C}{A C}\) and m_n = \(\frac{E F}{D F}\) By ____________, \(\frac{B C}{A C}=\frac{E F}{D F}\). Rewriting this proportion yields ___________,

By the Right Angles Congruence Theorem (Thin. 2.3), ___________, So. ∆ABC ~ ∆DEF by ___________ . Because corresponding angles of similar triangles are congruent, ∠BAC ≅∠EDF. By ___________, l || n.

Answer:

Question 42.
PROVING A THEOREM
Copy and complete the two-column proof 0f the second part of the Slopes of Perpendicular Lines Theorem (Theorem 3.14)
Given m_l m_n = – 1, l and n are nonvertical.
Prove l ⊥ n

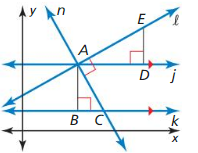
Statements	Reasons
1. mlmn = – 1	1. Given
2. ml = \(\frac{D E}{A D}\), mn = \(\frac{A B}{B C}\)	2. Definition of slope
3. \(\frac{D E}{A D} \cdot-\frac{A B}{B C}\) = – 1	3. ________________________________
4. \(\frac{D E}{A D}=\frac{B C}{A B}\)	4. Multiply each side of statement 3 by –\(\frac{B C}{A B}\).
5. \(\frac{D E}{B C}\) = ____________	5. Rewrite proportion.
6. ________________________________	6. Right Angles Congruence Theorem (Thm. 2.3)
7. ∆ABC ~ ∆ADE	7. ________________________________
8. ∠BAC ≅ ∠DAE	8. Corresponding angles of similar figures are congruent.
9. ∠BCA ≅ ∠CAD	9. Alternate Interior Angles Theorem (Thm. 3.2)
10. m∠BAC = m∠DAE, m∠BCA = m∠CAD	10. ________________________________
11. m∠BAC + m∠BCA + 90° = 180°	11. ________________________________
12. ________________________________	12. Subtraction Property of Equality
13. m∠CAD + m∠DAE = 90°	13. Substitution Property of Equality
14. m∠CAE = m∠DAE + m∠CAD	14. Angle Addition Postulate (Post. 1.4)
15. m∠CAE = 90°	15. ________________________________
16. ________________________________	16. Definition of perpendicular lines

Answer:

Statements	Reasons
1. mlmn = – 1	1. Given
2. ml = \(\frac{D E}{A D}\), mn = \(\frac{A B}{B C}\)	2. Definition of slope
3. \(\frac{D E}{A D} \cdot-\frac{A B}{B C}\) = – 1	3. Correspomsding sides are opposite
4. \(\frac{D E}{A D}=\frac{B C}{A B}\)	4. Multiply each side of statement 3 by –\(\frac{B C}{A B}\).
5. \(\frac{D E}{B C}\) = \(\frac { AB }{ AD } \)	5. Rewrite proportion.
6. Two right-angled triangles are said to be congruent to each other if the hypotenuse and one side of the right triangle are equal to the hypotenuse and the corresponding side of the other right-angled triangle.	6. Right Angles Congruence Theorem (Thm. 2.3)
7. ∆ABC ~ ∆ADE	7. According to the side angle side theorem.
8. ∠BAC ≅ ∠DAE	8. Corresponding angles of similar figures are congruent.
9. ∠BCA ≅ ∠CAD	9. Alternate Interior Angles Theorem (Thm. 3.2)
10. m∠BAC = m∠DAE, m∠BCA = m∠CAD	10. Congruent angles
11. m∠BAC + m∠BCA + 90° = 180°	11. △ABC is a right-angled triangle
12. m∠CAD + m∠DAE = 90°	12. Subtraction Property of Equality
13. m∠CAD + m∠DAE = 90°	13. Substitution Property of Equality
14. m∠CAE = m∠DAE + m∠CAD	14. Angle Addition Postulate (Post. 1.4)
15. m∠CAE = 90°	15. Right Angle
16. If two lines meet each other a an angle of 90°, then they are called the perpendicular lines.	16. Definition of perpendicular lines

Maintaining Mathematical proficiency

Find the coordinates of point P along the directed line segment AB so that AP to PB is the given ratio.

Question 43.
A(- 3, 6), B(2, 1); 3 to 2
Answer:

Question 44.
A(- 3, – 5), B(9, – 1); 1 to 3
Answer:
In order to divide the segment in the ratio 1 to 3, think of dividing the segment into 1 + 3 or 4 congruent pieces.
Point P is the point that is 1/4 of the way from point A to B.
Slope of AB = (-1 + 5)/(9+3) = 4/12 = 1/3 = rise/run
To find the coordinates of point P, add 1/4 of the run to the x-coordinate of A and 1/4 of the rise to the y-coordinate of A.
run = 1/4 × 3 = 3/4
rise = 1/4 × 1 = 1/4

Question 45.
A(1, – 2), B(8, 12); 4 to 3
Answer:

8.4 Proportionality Theorems

Exploration 1

Discovering a Proportionality Relationship

Work with a partner. Use dynamic geometry software to draw any ∆ABC.
a. Construct \(\overline{D E}\) parallel to \(\overline{B C}\) with endpoints on \(\overline{A B}\) and \(\overline{A C}\), respectively.

Answer:

b. Compare the ratios of AD to BD and AE to CE.
Answer:

c. Move \(\overline{D E}\) to other locations Parallel to \(\overline{B C}\) with endpoints on \(\overline{A B}\) and \(\overline{A C}\), and repeat part (b).
Answer:

d. Change ∆ABC and repeat parts (a) – (c) several times. Write a conjecture that summarizes your results.
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:

Exploration 2

Discovering a Proportionality Relationship

Work with a partner. Use dynamic geometry software to draw any AABC.

a. Bisect ∆B and plot point D at the intersection of the angle bisector and \(\overline{A C}\).
Answer:

b. Compare the ratios of AD to DC and BA to BC.
Answer:

c. Change ∆ABC and repeat parts (a) and (b) several times. Write a conjecture that summarizes your results.
Answer:

Communicate Your Answer

Question 3.
What proportionality relationships exist in a triangle intersected by an angle bisector or by a line parallel to one of the sides?

Answer:

• The proportionality relationship that exists in a triangle intersected by an angle bisector is it divides the opposite side into segments whose lengths are proportional to the lengths of the other two sides.
• The proportionality relationships that exist in a triangle by a line parallel to one side of a triangle intersects the other two sides, then divides the two sides proportionally.

Question 4.
Use the figure at the right to write a proportion.

Answer:
The line segment DE is parallel to the side AC then it divides the other two sides DA and EC proportionally.
DA/DB = EC/EB respectively

Lesson 8.4 Proportionality Theorems

Monitoring Progress

Question 1.
Find the length of \(\overline{Y Z}\).

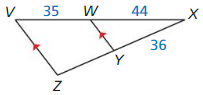
Answer:
YZ = \(\frac { 315 }{ 11 } \)

Explanation:
Triangle property thorem is \(\frac { XW }{ WV } \) = \(\frac { XY }{ YZ } \)
\(\frac { 44 }{ 35 } \) = \(\frac { 36 }{ YZ } \)
cross multiply the fractions
44 • YZ = 36 • 35
44 • YZ = 1260
YZ = \(\frac { 1260 }{ 44 } \)
YZ = \(\frac { 315 }{ 11 } \)

Question 2.
Determine whether \(\overline{P S}\) || \(\overline{Q R}\)

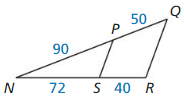
Answer:
\(\frac { PQ }{ PN } \) = \(\frac { 50 }{ 90 } \) = \(\frac { 5 }{ 9 } \)
\(\frac { SR }{ SN } \) = \(\frac { 40 }{ 72 } \) = \(\frac { 5 }{ 9 } \)
\(\frac { PQ }{ PN } \) = \(\frac { SR }{ SN } \) so PS is parallel to QR

Find the length of the given line segment.

Question 3.
\(\overline{B D}\)

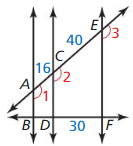
Answer:
\(\overline{B D}\) = 12

Explanation:
All the angles are congruent. So, \(\overline{A B}\), \(\overline{C D}\), \(\overline{E F}\) are parallel.
using the three parallel lines theorem
\(\frac { BD }{ DF } \) = \(\frac { AC }{ CE } \)
\(\frac { [latex]\overline{B D}\) }{ 30 } [/latex] = \(\frac { 16 }{ 40 } \)
\(\overline{B D}\) = \(\frac { 16 }{ 40 } \) • 30
\(\overline{B D}\) = 12

Question 4.
\(\overline{J M}\)

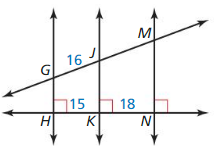
Answer:
\(\overline{J M}\) = \(\frac { 96 }{ 5 } \)

Explanation:
All the angles are congruent. So, \(\overline{G H}\), \(\overline{J K}\), \(\overline{M N}\) are parallel.
using the three parallel lines theorem
\(\frac { HK }{ KN } \) = \(\frac { GJ }{ JM } \)
\(\frac { 15 }{ 18 } \) = \(\frac { 16 }{ [latex]\overline{J M}\) } [/latex]
Cross multiply
15 • \(\overline{J M}\) = 16 • 18 = 288
\(\overline{J M}\) = \(\frac { 288 }{ 15 } \)
\(\overline{J M}\) = \(\frac { 96 }{ 5 } \)

Find the value of the variable.

Question 5.

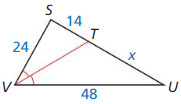
Answer:
x = 28

Explanation:
\(\overline{T V}\) is the angle bisector
So, \(\frac { ST }{ TU } \) = \(\frac { SV }{ VU } \)
\(\frac { 14 }{ x } \) = \(\frac { 24 }{ 48 } \)
cross multiply
24x = 14 • 48 = 672
x = \(\frac { 672 }{ 24 } \)
x = 28

Question 6.

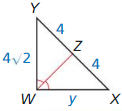
Answer:
x = 4√2

Explanation:
\(\overline{W Z}\) is the angle bisector
So, \(\frac { YZ }{ ZX } \) = \(\frac { YW }{ WX } \)
\(\frac { 4 }{ 4 } \) = \(\frac { 4√2 }{ x } \)
cross multiply
4x = 4 • 4√2 = 16√2
x = 4√2

Exercise 8.4 Proportionality Theorems

Vocabulary and Core Concept Check

Question 1.
COMPLETE THE STATEMENT
If a line divides two sides of a triangle proportionally, then it is ____________ to the third side. This theorem is knon as the ____________ .
Answer:

Question 2.
VOCABULARY
In ∆ABC, point R lies on \(\overline{B C}\) and \(\vec{A}\)R bisects ∆CAB. Write the proportionality statement for the triangle that is based on the Triangle Angle Bisector Theorem (Theorem 8.9).

Answer:
According to the triangle angle bisector theorem \(\frac { CR }{ BR } \) = \(\frac { AC }{ AB } \)

Monitoring Progress and Modeling with Mathematics

In Exercises 3 and 4, find the length of \(\overline{A B}\) .

Question 3.

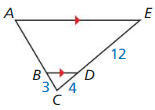
Answer:

Question 4.

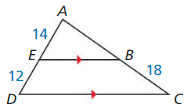
Answer:
\(\frac { AE }{ ED } \) = \(\frac { AB }{ BC } \)
\(\frac { 14 }{ 12 } \) = \(\frac { AB }{ 18 } \)
AB = \(\frac { 14 }{ 12 } \) • 18
AB = 21 units.

In Exercises 5 – 8, determine whether \(\overline{K M}\) || \(\overline{J N}\).

Question 5.

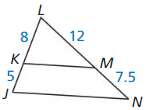
Answer:

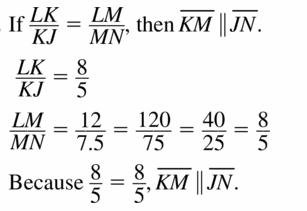
Question 6.

Answer:
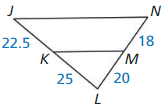
If \(\frac { JK }{ KL } \) = \(\frac { NM }{ ML } \), then KM || JN
\(\frac { JK }{ KL } \) = latex]\frac { 22.5 }{ 25 } [/latex] = latex]\frac { 9 }{ 10 } [/latex]
\(\frac { NM }{ ML } \) = \(\frac { 18 }{ 20 } \) = latex]\frac { 9 }{ 10 } [/latex]
\(\frac { JK }{ KL } \) = \(\frac { NM }{ ML } \)
Hence KM || JN

Question 7.

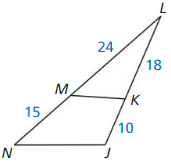
Answer:

Question 8.

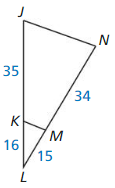
Answer:
If \(\frac { JK }{ KL } \) = \(\frac { NM }{ ML } \), then KM || JN
\(\frac { JK }{ KL } \) = latex]\frac {35 }{ 16 } [/latex]
\(\frac { NM }{ ML } \) = \(\frac { 34 }{ 15 } \)
\(\frac { JK }{ KL } \) ≠ \(\frac { NM }{ ML } \)
So, KM is not parallel to JN

CONSTRUCTION
In Exercises 9 – 12, draw a segment with the given length. Construct the point that divides the segment in the given ratio.
Question 9.
3 in.; 1 to 4
Answer:

Question 10.
2 in.; 2 to 3

Answer:
Construct a 2 inch segment and divide the segment into 2 + 3 or 5 congruent pieces. Point P is the point that is \(\frac { 1 }{ 5 } \) of the way from point A to point B.

Question 11.
12 cm; 1 to 3
Answer:

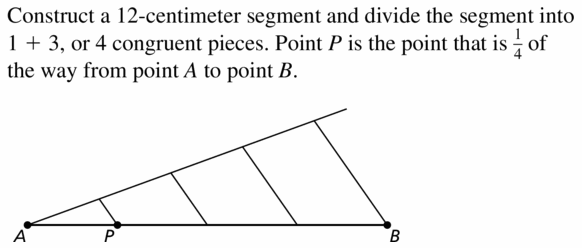
Question 12.
9 cm ; 2 to 5
Answer:
Construct a 9 cm segment and divide the segment into 2 + 5 or 7 congruent pieces. Point p is the point that is \(\frac { 1 }{ 7 } \) of the way from point A to point B.

In Exercises 13 – 16, use the diagram to complete the proportion.

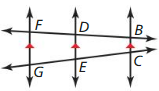
Question 13.

Answer:

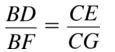
Question 14.

Answer:
\(\frac { CG }{ EG } \) = \(\frac { BF }{ DF } \)

Question 15.

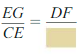
Answer:

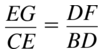
Question 16.

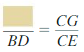
Answer:
\(\frac { BF }{ BD } \) = \(\frac { CG }{ CE } \)

In Exercises 17 and 18, find the length of the indicated line segment.

Question 17.
\(\overline{V X}\)

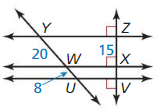
Answer:

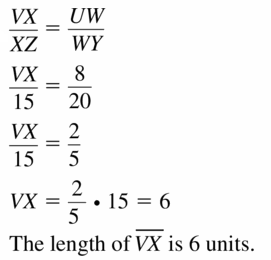
Question 18.
\(\overline{S U}\)

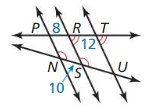
Answer:
\(\frac { SU }{ NS } \) = \(\frac { RT }{ PR } \)
\(\frac { SU }{ 10 } \) = \(\frac { 12 }{ 8 } \)
SU = \(\frac { 12 }{ 8 } \) • 10
SU = 10

In Exercises 19 – 22, find the value of the variable.

Question 19.

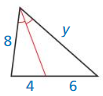
Answer:

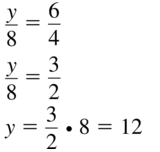
Question 20.

Answer:
\(\frac { z }{ 1.5 } \) = \(\frac { 3 }{ 4.5 } \)
z = \(\frac { 3 }{ 4.5 } \) • 1.5
z = 1

Question 21.

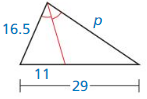
Answer:

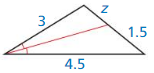
Question 22.

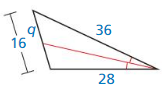
Answer:
\(\frac { q }{ 16 – q } \) = \(\frac { 36 }{ 28 } \)
28q = 36 (16 – q)
28q = 576 – 36q
28q + 36q = 576
64q = 576
q = 9

Question 23.
ERROR ANALYSIS
Describe and correct the error in solving for x.

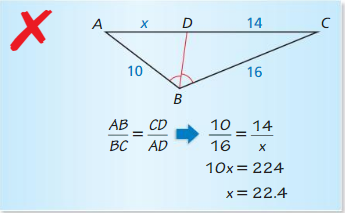
Answer:

Question 24.
ERROR ANALYSIS
Describe and correct the error in the students reasoning.

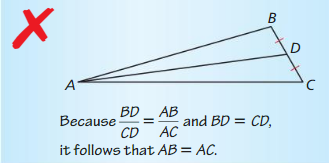
Answer:
\(\frac { BD }{ CD } \) = \(\frac { AB }{ AC } \)
BD = CD
So, 1 = \(\frac { AB }{ AC } \)
AC = AB

MATHEMATICAL CONNECTIONS
In Exercises 25 and 26, find the value of x for which \(\overline{P Q}\) || \(\overline{R S}\).

Question 25.

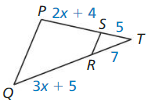
Answer:

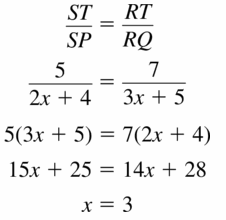
Question 26.

Answer:
\(\frac { PR }{ RT } \) = \(\frac { QS }{ ST } \)
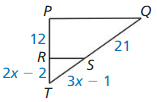
\(\frac { 12 }{ 2x – 2 } \) = \(\frac { 21 }{ 3x – 1 } \)
12(3x – 1) = 21(2x – 2)
36x – 12 = 42x – 42
42x – 36x = 42 – 12
6x = 30
x = 5

Question 27.
PROVING A THEOREM
Prove the Triangle Proportionality Theorem (Theorem 8.6).

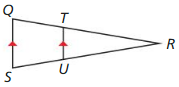
Given \(\overline{Q S}\) || \(\overline{T U}\)
Prove \(\frac{Q T}{T R}=\frac{S U}{U R}\)
Answer:

Question 28.
PROVING A THEOREM
Prove the Converse of the Triangle Proportionality Theorem (Theorem 8.7).

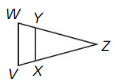
Given \(\frac{Z Y}{Y W}=\frac{Z X}{X V}\)
Prove \(\overline{Y X}\) || \(\overline{W V}\)
Answer:
ZY/YW = ZX/XV — (1)
1 + ZY/YW = 1 + ZX/XV
(YW + ZY)/YW = (XV + ZX)/XV
ZW/YW = ZV/XV (∠Z is common for ΔZXY and ΔZVW)
ZW/YW = ZV/XV
ΔZXY and ΔZVW are proportional
ΔZXY ≈ ΔZVW
∠ZYW = ∠ZWV
YX is paralle to WV.

Question 29.
MODELING WITH MATHEMATICS
The real estate term lake frontage refers to the distance along the edge of a piece of property that touches a lake.

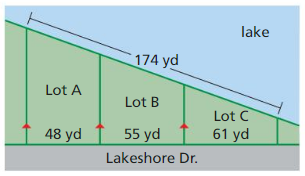
a. Find the lake frontage (to the nearest tenth) of each lot shown.
b. In general, the more lake frontage a lot has, the higher its selling price. Which lot(s) should be listed for the highest price?
c. Suppose that low prices are in the same ratio as lake frontages. If the least expensive lot is $250,000, what are the prices of the other lots? Explain your reasoning.
Answer:

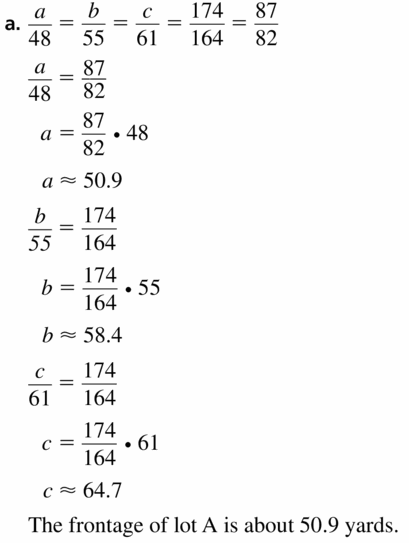
Question 30.
USING STRUCTURE
Use the diagram to find the values of x and y.

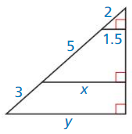
Answer:
\(\frac { 5 }{ 2 } \) = \(\frac { x }{ 1.5 } \)
x = \(\frac { 5 }{ 2 } \) • 1.5
x = 3.75
\(\frac { 3 }{ 7 } \) = \(\frac { y }{ 5.25 } \)
y = \(\frac { 3 }{ 7 } \) • 5.25
y = 2.25

Question 31.
REASONING
In the construction on page 447, explain why you can apply the Triangle Proportionality Theorem (Theorem 86) in Step 3.
Answer:

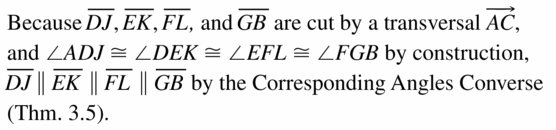
Question 32.
PROVING A THEOREM
Use the diagram with the auxiliary line drawn to write a paragraph proof of the Three Parallel Lines Theorem (Theorem 8.8).
Given K₁ || K₂ || K₃
Prove \(\frac{C B}{B A}=\frac{D E}{E F}\)

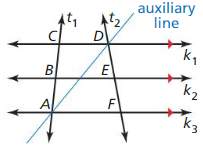
Answer:
From the diagram, we can see that K₁ || K₂ || K₃
Those three parallel lines interest two traversals t₁, t₂
So, \(\frac{C B}{B A}=\frac{D E}{E F}\)

Question 33.
CRITICAL THINKING
In ∆LMN, the angle bisector of ∠M also bisects \(\overline{L N}\). Classify ∆LMN as specifically as possible. Justify your answer.
Answer:

Question 34.
HOW DO YOU SEE IT?
During a football game, the quarterback throws the ball to the receiver. The receiver is between two defensive players, as shown. If Player 1 is closer to the quarterback when the ball is thrown and both defensive players move at the same speed, which player will reach the receiver first? Explain your reasoning.

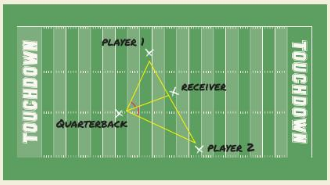
Answer:
As per the image, player 1 is closer to the receiver. So, player 1 will reach the receiver first.

Question 35.
PROVING A THEOREM
Use the diagram with the auxiliary lines drawn to write a paragraph proof of the Triangle Angle Bisector Theorem (Theorem 8.9).
Given ∠YXW ≅ ∠WXZ
prove \(\frac{Y W}{W Z}=\frac{X Y}{X Z}\)

Answer:

Question 36.
THOUGHT PROVOKING
Write the converse of the Triangle Angle Bisector Theorem (Theorem 8.9). Is the converse true? Justify your answer.
Answer:
Stating the converse of the Triangle Angle Bisector Theorem.
The converse of the Triangle Angle Bisector Theorem states that if a ray divides a side of a triangle into segments whose lengths are proportional to the lengths of the other two sides, it bisects the angle opposite to the first side.
AB/AC = BD/DC
Showing ΔABD and ΔCDE are similar
By construction, CE ∣∣AB
So ∠CED≅∠DAB
And ∠ECD ≅ ∠DBA
So ΔABD∼ΔCDE
BD/CD = AB/CE
AC = CE
∠CED≅∠DAB and
∠CAD≅∠DAB
So, ∠CED≅∠DAB
Hence AD is an angle bisector of ∠BAC

Question 37.
REASONING
How is the Triangle Midsegment Theorem (Theorem 6.8) related to the Triangle Proportionality Theorem (Theorem 8.6)? Explain your reasoning.
Answer:

Question 38.
MAKING AN ARGUMENT
Two people leave points A and B at the same time. They intend to meet at point C at the same time. The person who leaves point A walks at a speed of 3 miles per hour. You and a friend are trying to determine how fast the person who leaves point B must walk. Your friend claims you need to know the length of \(\overline{A C}\). Is your friend correct? Explain your reasoning.

Answer:
My self starts walking from point A with a speed of 3 miles per hour and reaches point C.
My friend starts walking from point B with x speed and reaches point C.
\(\frac { AD }{ DC } \) = \(\frac { BE }{ CE } \)
I have to travel from A to C. So, I need to know distance between AC.
Therefore, my friend is correct.

Question 39.
CONSTRUCTION
Given segments with lengths r, s, and t, construct a segment of length x, such that \(\frac{r}{s}=\frac{t}{x}\)

Answer:

Question 40.
PROOF
Prove Ceva’s Theorem: If P is any point inside ∆ABC, then \(\frac{A Y}{Y C} \cdot \frac{C X}{X B} \cdot \frac{B Z}{Z A}\) = 1

(Hint: Draw segments parallel to \(\overline{B Y}\) through A and C, as shown. Apply the Triangle Proportionality Theorem (Theorem 8.6) to ∆ACM. Show that ∆APN ~ ∆MPC, ∆CXM ~ ∆BXP, and ∆BZP ~ ∆AZN.)
Answer:
Drawing line segments AN and CM such that AN ∣∣ YB ∣∣ CM and using the Triangle Proportionality Theorem
AY/YC = AP/PM
Using the Vertical Angle Congruence theorem
∠MPC≅∠NPA
Since AN∣∣CM, using the Alternate Angles Theorem
∠NAP≅∠PMC
By AA Similarity Theorem
ΔAPN∼ΔMPC
Through corresponding parts of similar triangles
AP/MP = PN/PC
PN/PC = AN/MC
Using the Vertical Angle Congruence theorem
∠BXP ≅ ∠CXM
Since BP∣∣CM, using the Alternate Angles Theorem
∠PBX ≅ ∠XCM
By AA Similarity Theorem
ΔCXM ∼ ΔBXP
Through corresponding parts of similar triangles
CX/BX = XM/XP
XM/XP = CM/BP
Using the Vertical Angle Congruence theorem
∠AZN ≅∠BZP
Since AN∣∣BP, using the Alternate Angles Theorem
∠ANZ≅∠BPZ
By AA Similarity Theorem
ΔBZP∼ΔAZN
Through corresponding parts of similar triangles
BZ/AZ = ZP/ZN
ZP/ZN = BP/AN
AY/YC = AP/PM
AP/MP = AN/MC
Hence AY/YC = AN/MC
CX/BX = CM/BP
BZ/AZ = BP/AN
Simplifying
AY/AC × CX/XB × BZ/ZA
AY/YC . CX/XB . BZ/ZA = AN/MC . CM/BP . BP/AN = 1

Maintaining Mathematical Proficiency

Use the triangle.

Question 41.
Which sides are the legs?
Answer:

Question 42.
Which side is the hypotenuse?
Answer:
The leg c is the hypotenuse.

Solve the equation.

Question 43.
x² = 121
Answer:

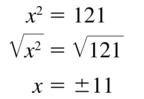
Question 44.
x² + 16 = 25
Answer:
x² + 16 = 25
x² = 25 – 16
x² = 9
x = ∓3

Question 45.
36 + x² = 85
Answer:

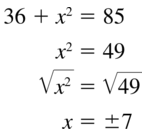
Similarity Review

8.1 Similar Polygons

Find the scale factor. Then list all pairs of congruent angles and write the ratios of the corresponding side lengths in a statement of proportionality.

Question 1.
ABCD ~ EFGH

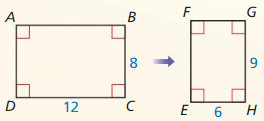
Answer:
\(\frac { BC }{ CD } \) = \(\frac { 8 }{ 12 } \) = \(\frac { 2 }{ 3 } \)
\(\frac { EH }{ GH } \) = \(\frac { 6 }{ 9 } \) = \(\frac { 2 }{ 3 } \)
So, scale factor = \(\frac { 2 }{ 3 } \)

Question 2.
∆XYZ ~ ∆RPQ

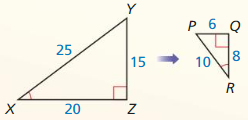
Answer:
longer sides: \(\frac { 10 }{ 25 } \) = \(\frac { 2 }{ 5 } \)
shorter sides: \(\frac { 6 }{ 15 } \) = \(\frac { 2 }{ 5 } \)
remaining sides: \(\frac { 8 }{ 20 } \) = \(\frac { 2 }{ 5 } \)
So, scale factor = \(\frac { 2 }{ 5 } \)

Question 3.
Two similar triangles have a scale factor of 3 : 5. The altitude of the larger triangle is 24 inches. What is the altitude of the smaller triangle?
Answer:
Scale factor of smaller triangle to larger traingle is \(\frac { 3 }{ 5 } \) and larger traingle altitude is 24 inches
Let x be the smaller triangle altitude
\(\frac { altitude of smaller triangle }{ altitude of larger traingle } \) = scale factor
\(\frac { x }{ 24 } \) = \(\frac { 3 }{ 5 } \)
x = \(\frac { 3 }{ 5 } \) • 24
x = 14.4

Question 4.
Two similar triangles have a pair of corresponding sides of length 12 meters and 8 meters. The larger triangle has a perimeter of 48 meters and an area of 180 square meters. Find the perimeter and area of the smaller triangle.
Answer:
Scale factor = \(\frac { 2 }{ 3 } \)
perimeter of smaller triangle = 32
Area of smaller triangle = 80

Explanation:
The scale factor of smaller to larger traingle = \(\frac { 8 }{ 12 } \) = \(\frac { 2 }{ 3 } \)
\(\frac { perimeter of smaller triangle }{ perimeter of larger triangle } \) = scale factor\(\frac { perimeter of smaller triangle }{ 48 } \) = \(\frac { 2 }{ 3 } \)
perimeter of smaller triangle = \(\frac { 2 }{ 3 } \) • 48
perimeter of smaller triangle = 32
\(\frac { Area of smaller triangle }{ Area of larger triangle } \) = (scale factor)²
\(\frac { Area of smaller triangle }{ 180 } \) = ( \(\frac { 2 }{ 3 } \))²
Area of smaller triangle = \(\frac { 4 }{ 9 } \) • 180
= 80

8.2 Proving Triangle Similarity by AA

Show that the triangles are similar. Write a similarity statement.

Question 5.

Answer:
m∠RQS = m∠UTS = 30°.
△QRS and △STU are similar as per the AA similarity theorem.

Question 6.

Answer:
m∠CAB = 60°, m∠DEF = 30°
△ABC and △DEF are not similar as per the AA similarity theorem.

Question 7.
A cellular telephone tower casts a shadow that is 72 feet long, while a nearby tree that is 27 feet tall casts a shadow that is 6 feet long. How tall is the tower?
Answer:
\(\frac { shadow of tree }{ shadow of tower } \) = \(\frac { height of tree }{ height of tower } \)
\(\frac { 6 }{ 72 } \) = \(\frac { 27 }{ x } \)
6x = 1944
x = 324 ft
The height of the tower is 324 ft.

8.3 Proving Triangle Similarity by SSS and SAS

Use the SSS Similarity Theorem (Theorem 8.4) or the SAS Similarity Theorem (Theorem 8.5) to show that the triangles are similar.

Question 8.

Answer:
\(\frac { DE }{ CD } \) = \(\frac { 7 }{ 3.5 } \) = 2
\(\frac { AB }{ BC } \) = \(\frac { 8 }{ 4 } \) = 2
\(\frac { DE }{ CD } \) = \(\frac { AB }{ BC } \)
So, BD is parallel to AE.

Question 9.

Answer:
\(\frac { QU }{ TU } \) = \(\frac { 9 }{ 4.5 } \) = 2
\(\frac { QR }{ SR } \) = \(\frac { 14 }{ 7 } \) = 2
\(\frac { QU }{ TU } \) = \(\frac { QR }{ SR } \)
So, ST is parallel to RU.

Question 10.
Find the value of x that makes ∆ABC ~ ∆DEF

Answer:
\(\frac { 24 }{ 6 } \) = 4
\(\frac { 32 }{ 2x } \) = 4
32 = 8x
x = \(\frac { 32 }{ 8 } \)
x = 4

8.4 Proportionality Theorems

Determine whether \(\overline{A B}\) || \(\overline{C D}\)

Question 11.

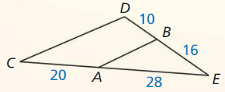
Answer:
\(\frac { DB }{ BE } \) = \(\frac { 10 }{ 16 } \) = \(\frac { 5 }{ 8 } \)
\(\frac { CA }{ AE } \) = \(\frac { 20 }{ 28 } \) = \(\frac { 5 }{ 7 } \)
\(\frac { DB }{ BE } \) ≠ \(\frac { CA }{ AE } \)
So, CD and AB are not parallel.

Question 12.

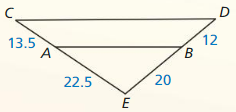
Answer:
\(\frac { DB }{ BE } \) = \(\frac { 12 }{ 20 } \) = \(\frac { 3 }{ 5 } \)
\(\frac { CA }{ AE } \) = \(\frac { 13.5 }{ 22.5 } \) = \(\frac { 3 }{ 5 } \)
\(\frac { DB }{ BE } \) = \(\frac { CA }{ AE } \)
So, AB and CD are parallel.

Question 13.
Find the length of \(\overline{Y B}\).

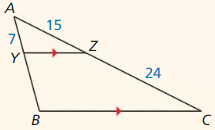
Answer:
\(\frac { ZC }{ AZ } \) = \(\frac { 24 }{ 15 } \) = \(\frac { 8 }{ 5 } \)
\(\frac { YB }{ AY } \) = \(\frac { ZC }{ AZ } \)
\(\frac { YB }{ 7 } \) = \(\frac { 8 }{ 5 } \)
YB = \(\frac { 8 }{ 5 } \) • 7
YB = \(\frac { 56 }{ 5 } \)
The length of \(\overline{Y B}\) is \(\frac { 56 }{ 5 } \)

Find the length of \(\overline{A B}\).

Question 14.

Answer:
\(\frac { AB }{ 7 } \) = \(\frac { 6 }{ 4 } \)
\(\overline{A B}\) = \(\frac { 6 }{ 4 } \) • 7
\(\overline{A B}\) = \(\frac { 42 }{ 4 } \)
\(\overline{A B}\) = \(\frac { 21 }{ 2 } \)
The length of \(\overline{A B}\) is \(\frac { 21 }{ 2 } \).

Question 15.

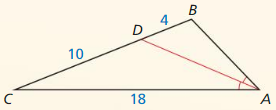
Answer:
\(\frac { DB }{ CD } \) = \(\frac { AB }{ AC } \)
\(\frac { 4 }{ 10 } \) = \(\frac { AB }{ 18 } \)
\(\frac { 2 }{ 5 } \) = \(\frac { AB }{ 18 } \)
AB = \(\frac { 36 }{ 5 } \)

Similarity Test

Determine whether the triangles are similar. If they are, write a similarity statement. Explain your reasoning.

Question 1.

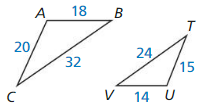
Answer:
Longer sides: \(\frac { 32 }{ 24 } \) = \(\frac { 4 }{ 3 } \)
shorter sides: \(\frac { 18 }{ 14 } \) = \(\frac { 9 }{ 7 } \)
remaining sides: \(\frac { 20 }{ 15 } \) = \(\frac { 4 }{ 3 } \)
Those are not equal.
So, triangles are not similar.

Question 2.

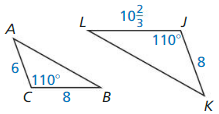
Answer:
\(\frac { AC }{ KJ } \) = \(\frac { 6 }{ 8 } \) = \(\frac { 3 }{ 4 } \)
\(\frac { BC }{ JL } \) = \(\frac { 8 }{ [latex]\frac { 32 }{ 3 } \) } [/latex] = \(\frac { 3 }{ 4 } \)
\(\frac { AC }{ KJ } \) = \(\frac { BC }{ JL } \)
∠C = ∠J
So, △ABC and △JLK are similar.

Question 3.

Answer:
\(\frac { XY }{ XW } \) = \(\frac { PZ }{ PW } \)

Find the value of the variable.

Question 4.

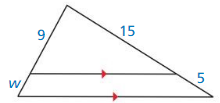
Answer:
\(\frac { 9 }{ w } \) = \(\frac { 15 }{ 5 } \)
\(\frac { 9 }{ w } \) = 3
9 = 3w
w = 3

Question 5.

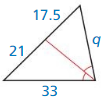
Answer:
\(\frac { 17.5 }{ 21 } \) = \(\frac { q }{ 33 } \)
q = \(\frac { 17.5 }{ 21 } \) • 33
q = \(\frac { 55 }{ 2 } \)

Question 6.

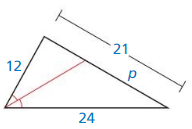
Answer:
\(\frac { 21 – p }{ p } \) = \(\frac { 12 }{ 24 } \)
\(\frac { 21 – p }{ p } \) = \(\frac { 1 }{ 2 } \)
cross multiply
2(21 – p) = p
42 – 2p = p
42 = p + 2p
42 = 3p
p = 14

Question 7.
Given ∆QRS ~ ∆MNP, list all pairs of congruent angles, Then write the ratios of the corresponding side lengths in a statement of proportionality.

Answer:
The pairs of congruent anglres are m∠QRS, m∠RSQ, m∠SQR, m∠MNP, m∠NPM, m∠PMN.
The ratios of side lengths are \(\frac { RQ }{ MN } \), \(\frac { QS }{ MP } \), \(\frac { RS }{ NP } \)

Use the diagram.

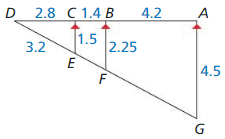
Question 8.
Find the length of \(\overline{E F}\).

Answer:
\(\frac { DE }{ EF } \) = \(\frac { CD }{ BC } \)
\(\frac { 3.2 }{ EF } \) = \(\frac { 2.8 }{ 1.4 } \)
EF = 1.6
The length of \(\overline{E F}\) is 1.6

Question 9.
Find the length of \(\overline{F G}\).

Answer:
\(\frac { EF }{ FG } \) = \(\frac { BC }{ AB } \)
\(\frac { 1.6 }{ FG } \) = \(\frac { 1.4 }{ 4.2 } \)
FG = 4.8
The length of \(\overline{F G}\) is 4.8

Question 10.
Is quadrilateral FECB similar to quadrilateral GFBA? If so, what is the scale factor of the dilation that maps quadrilateral FECB to quadrilateral GFBA?

Answer:
The scale factor of dilation from quadrilateral FECB to quadrilateral GFBA is \(\frac { GF }{ FE } \)

Question 11.
You are visiting the Unisphere at Flushing Meadows Corona Park in New York. To estimate the height of the stainless steel model of Earth. you place a mirror on the ground and stand where you can see the top of the model in the mirror. Use the diagram to estimate the height of the model. Explain why this method works.
Answer:
We know that the corresponding sides of a similar triangle are proportional
height of Unisphere/distance of Unisphere from mirror = height of person/distance of the person from mirror
x/100 = 5.6/4
x = 5.6 × 100/4
x = 140
Thus the estimated height of the tree = 140 ft

Question 12.
You are making a scale model of a rectangular park for a school project. Your model has a length of 2 feet and a width of 1.4 feet. The actual park is 800 yards long. What are the perimeter and area of the actual park?

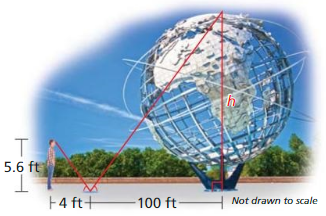
Answer:
we know that 1 yard = ft
As per the similarity theorem
\(\frac { AD }{ EH } \) = \(\frac { AB }{ EF } \)
\(\frac { 2 }{ 800.3 } \) = \(\frac { 1.4 }{ EF } \)
EF = 1200 • 1 • 4
EF = 1680
Perimete of the park P = 2(1680 + 2400)
= 2(4080) = 8160 ft
Area of the actual park = 1680 • 2400 = 4,032,000 sq ft
Therefore, perimeter of the actual park = 8160 ft
area of the actual park is 4,032,000 sq ft.

Question 13.
In a Perspective drawing, lines that are parallel in real life must meet at a vanishing point on the horizon. To make the train cars in the drawing appear equal in length, they are drawn so that the lines connecting the opposite corners of each car are parallel. Use the dimensions given and the yellow parallel lines to find the length of the bottom edge of the drawing of Car 2.

Answer:
\(\frac { 5.4 }{ 10.6 } \) = \(\frac { 5.4 + C }{ 19 } \)
C = \(\frac { 45.36 }{ 10.6 } \)
\(\frac { (19 – x – 8.4) }{ (19 – 8.4) } \) = \(\frac { 5.4 }{ 5.4 + c } \)
\(\frac { 19 – 8.4 }{ 19 } \) = \(\frac { c2 + 5.4 }{ c1 + c2 + 5.4 } \)
\(\frac { 19 – 8.4 }{ 19 } \) = \(\frac { 5.4 }{ 5.4 + c2 } \)
c1 = 7.6, c2 = 4.2, x = 4.6
The length of car 2 is 4.2 cm.

Similarity Cumulative Assessment

Question 1.
Use the graph of quadrilaterals ABCD and QRST.

a. Write a composition of transformations that maps quadrilateral ABCD to quadrilateral QRST.
Answer:
The scale factor = \(\frac { AD }{ QT } \) = \(\frac { 2 }{ 1.5 } \)

b. Are the quadrilaterals similar? Explain your reasoning.
Answer:
No.
\(\frac { AD }{ QT } \) = \(\frac { 2 }{ 1.5 } \)
\(\frac { CD }{ TS } \) = \(\frac { 2.8 }{ 1.4 } \) = 2
So, quadrilaterals are not similar.

Question 2.
In the diagram. ABCD is a parallelogram. Which congruence theorem(s) could you Use to show that ∆AED ≅ ∆CEB? Select all that apply.

SAS Congruence Theorem (Theorem 5.5)
Answer:
It states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent.

SSS Congruence Theorem (Theorem 5.8)
Answer:
If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule.

HL Congruence Theorem (Theorem 5.9)
Answer:
A given set of triangles are congruent if the corresponding lengths of their hypotenuse and one leg are equal.

ASA Congruence Theorem (Theorem 5. 10)
Answer:
If any two angles and the side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule

AAS Congruence Theorem (Theorem 5. 11)
Answer:
AAS stands for Angle-angle-side. When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle, then the triangles are said to be congruent.

Question 3.
By the Triangle Proportionality Theorem (Theorem 8.6), \(\frac{V W}{W Y}=\frac{V X}{X Z}\) In the diagram, VX > VW and XZ > WY. List three possible values for VX and XZ.

Answer:
\(\frac{V W}{W Y}=\frac{V X}{X Z}\)
\(\frac{ 4 }{6}=\frac{V X}{X Z}\)
The possible values of VX are greater than 4 means 5, 6, 7, . . .
The possible values of XZ are greater than 6 means 7, 8, 9, . .

Question 4.
The slope of line l is – \(\frac{3}{4}\). The slope of line n is \(\frac{4}{3}\) What must be true about lines l and n ?
(A) Lines l and n are parallel.
(B) Lines l and n arc perpendicular.
(C) Lines l and n are skew.
(D) Lines l and n are the same line.
Answer:
The slope of l = – \(\frac{3}{4}\)
Slope of n = \(\frac{4}{3}\)
lines slopes are reciprocal and opposite. So, they are perpendicular.

Question 5.
Enter a statement or reason in each blank to complete the two-column proof.

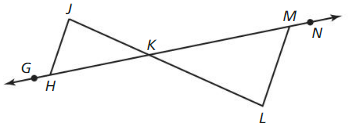
Given \(\frac{K J}{K L}=\frac{K H}{K M}\)
Prove ∠LMN ≅ ∠JHG

Statements	Reasons
1. \(\frac{K J}{K L}=\frac{K H}{K M}\)	1. Given
2. ∠JKH ≅ ∠LKM	2. ________________________
3. ∆JKH ~ ∆LKM	3. ________________________
4. ∠KHJ ≅∠KML	4. ________________________
5. _______________________	5. Definition of congruent angles
6. m∠KHJ + m∠JHG = 180°	6. Linear Pair Postulate (Post. 18)
7. m∠JHG = 180° – m∠KHJ	7. ________________________
8. m∠KML + m∠LMN = 180°	8. ________________________
9. ________________________	9. Subtraction Property of Equality
10. m∠LMN = 180° – m∠KHJ	10. ________________________
11. ________________________	11. Transitive Property of Equality
12. ∠LMN ≅ ∠JHG	12. ________________________

Answer:

Statements	Reasons
1. \(\frac{K J}{K L}=\frac{K H}{K M}\)	1. Given
2. ∠JKH ≅ ∠LKM	2. Opposite angles
3. ∆JKH ~ ∆LKM	3. By SSS rule if two side lengths of two triangles are proportional then triangles are similar.
4. ∠KHJ ≅∠KML	4. Alternate interior angles
5. Congruent angles are angles with the exactly the same measure	5. Definition of congruent angles
6. m∠KHJ + m∠JHG = 180°	6. Linear Pair Postulate (Post. 18)
7. m∠JHG = 180° – m∠KHJ	7. Subtraction Property of Equality
8. m∠KML + m∠LMN = 180°	8. Linear Pair Postulate
9. m∠LMN + m∠KML – m∠KML = 180 – m∠KML	9. Subtraction Property of Equality
10. m∠LMN = 180° – m∠KHJ	10. Transitive property of equuality
11. m∠JHG = 180 – m∠KML	11. Transitive Property of Equality
12. ∠LMN ≅ ∠JHG	12. Transitive property of equality

Question 6.
The coordinates of the vertices of ∆DEF are D(- 8, 5), E(- 5, 8), and F(- 1, 4), The coordinates of the vertices of ∆JKL are J(16, – 10), K(10, – 16), and L(2, – 8), ∠D ≅ ∠J. Can you show that ∆DEF ∆JKL by using the AA Similarity Theorem (Theorem 8.3)? If so, do so by listing the congruent corresponding angles and writing a similarity transformation that maps ∆DEF to ∆JKL. If not, explain why not.
Answer:
AA similarity theorem states that ∠D = ∠J. So, ∆DEF and ∆JKL are similar.

Question 7.
Classify the quadrilateral using the most specific name.

rectangle     square    parallelogram    rhombus
Answer: Parallelogram is a quadrilateral in which both pairs of opposite sides are parallel.

Question 8.
‘Your friend makes the statement “Quadrilateral PQRS is similar to quadrilateral WXYZ.” Describe the relationships between corresponding angles and between corresponding sides that make this statement true.

Answer:
When 2 figures are similar, then their corresponding angles are congruent and their corresponding lengths are proportional. hence if PQRS is similar to wxyZ, then the following statements are true.
∠P = ∠W, ∠Q = ∠X, ∠R = ∠Y and ∠S = ∠Z and
\(\frac { PQ }{ WX } \) = \(\frac { QR }{ XY } \) = \(\frac { RS }{ YZ } \) = \(\frac { PS }{ WZ } \) = k
Here is a constant of proportionality.