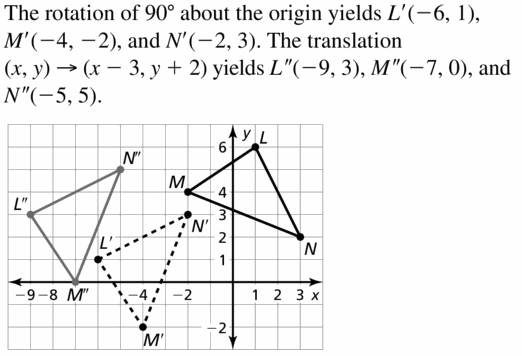
Your Practice Session without Big Ideas Math Geometry Answers Chapter 4 Transformations is incomplete. Resolve all your queries taking the help of the BIM Math Geometry Ch 4 Transformations Solution Key prepared by subject experts. All the Solutions given in the Big Ideas Math Textbook Geometry Chapter 4 Transformations Answer Key are explained in a detailed way as per the latest Common Core Curriculum syllabus guidelines.
Improve your subject knowledge and master the concepts of Transformations Big Ideas Math Geometry Chapter 4 by practicing the questions available frequently. Big Ideas Math Geometry Answers Chapter 4 Transformations covers questions related to Exercises, Practice Tests, Cumulative Assessments, Chapter Test, Review Tests, etc. Make the most out of them and clear the exam with flying colors.
Big Ideas Math Book Geometry Answer Key Chapter 4 Transformations
Become Pro in Maths and gain deeper insights on each and every concept of Big Ideas Geometry Chapter 4 Transformations Answer Key through the direct links available. Just tap on them and learn the respective topics in no time. Clear your doubts taking the help of the Topicwise BIM Geometry Chapter 4 Transformations for free of cost and prepare whenever you need.
Transformations
- Transformations Maintaining Mathematical Proficiency – Page 171
- Transformations Mathematical Practices – Page 172
Lesson: 1 Translations
- 4.1 Translations – Page(173-180)
- Lesson 4.1 Translations – Page(174-177)
- Exercise 4.1 Translations – Page(178-180)
Lesson: 2 Reflections
- 4.2 Reflections – Page 181
- Lesson 4.2 Reflections – Page(182-185)
- Exercise 4.2 Reflections – Page(186-188)
Lesson: 3 Rotations
- 4.3 Rotations – Page(189-196)
- Lesson 4.3 Rotations – Page(190-193)
- Exercise 4.3 Rotations – Page(194-196)
Quiz
Lesson: 4 Congruence and Transformations
- 4.4 Congruence and Transformations – Page(199-206)
- Lesson 4.4 Congruence and Transformations – Page(200-203)
- Exercise 4.4 Congruence and Transformations – Page(204-206)
Lesson: 5 Dilations
Lesson: 6 Similarity and Transformations
- 4.6 Similarity and Transformations – Page(215-220)
- Lesson 4.6 Similarity and Transformations – Page(216-218)
- Exercise 4.6 Similarity and Transformations – Page(219-220)
Review
- Transformations Chapter Review – Page(222-224)
- Transformations Test – Page 225
- Transformations Cumulative Assessment – Page(226-227)
Transformations Maintaining Mathematical Proficiency
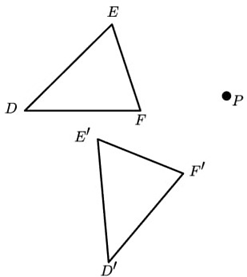
Tell whether the red figure is a translation, reflection, rotation, or dilation of the blue figure.
Question 1.
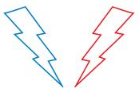
Answer: The red figure is the mirror image of the blue figure so it is a reflection.
Question 2.
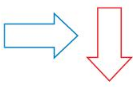
Answer: The blue figure turns to form the red figure so it is a rotation.
Question 3.
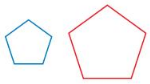
Answer: A dilation produces an image similar to the original figure. So, the blue polygon is a dilation of the red figure.
Question 4.
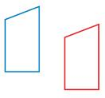
Answer: The blue figure is similar to the red figure and one is a dilation of the other.
Tell whether the two figures are similar. Explain your reasoning.
Question 5.

Answer:
Length of A/Length of B = 12/14 = 6/7
Width of A/Width of B = 5/7
Thus Rectangle A and Rectangle B are not similar.
Question 6.
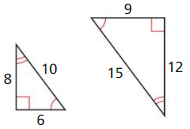
Answer:
Base of triangle A/Base of triangle B = 6/9 = 2/3
Height of triangle A/Height of triangle B = 8/12 = 2/3
Hypotenuse of triangle A/Hypotenuse of triangle B = 10/12 = 5/6
Triangle A and Triangle B are similar.
Question 7.
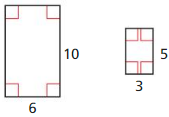
Answer:
Length of A/Length of B = 6/3 = 2
Width of A/Width of B = 10/5 = 2
The two figures are similar.
Transformations Mathematical Practices
Monitoring Progress
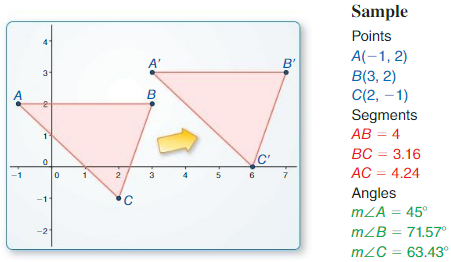
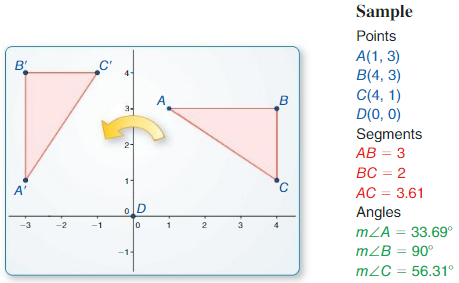
Use dynamic geometry software to draw the polygon with the given vertices. Use the software to find the side lengths and angle measures of the polygon. Round your answers to time nearest hundredth.
Question 1.
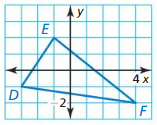
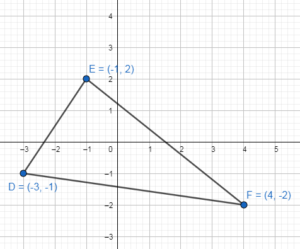
A(0, 2), B(3, – 1), C(4, 3)
Answer:
Points:
A(0, 2), B(3, – 1), C(4, 3)
Segments:
AB = 3 units
BC = 4 units
AC = 4 units
Question 2.
A(- 2, 1), B(- 2, – 1), C(3, 2)
Answer:
points:
A(- 2, 1), B(- 2, – 1), C(3, 2)
Segments:
AB = 2 units
BC = 5 units
AC = 5 units
Question 3.
A(1, 1), B(- 3, 1), C(- 3, – 2), D(1, – 2)
Answer:
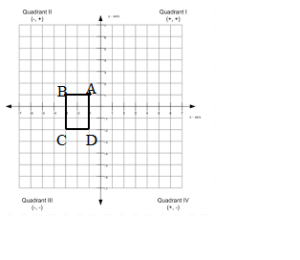
Points:
A(1, 1), B(- 3, 1), C(- 3, – 2), D(1, – 2)
Segments:
AB = 2 units
BC = 3 units
DC = 2 units
AD = 3 units
Angles:
∠A = ∠B = ∠C = ∠D = 90°
Question 4.
A(1, 1) B(- 3, 1), C(- 2, – 2), D(2, – 2)
Answer:
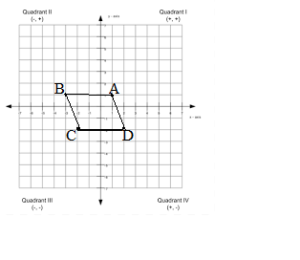
Points:
A(1, 1) B(- 3, 1), C(- 2, – 2), D(2, – 2)
Segments:
AB = 4 units
BC = 4 units
CD = 4 units
DA = 4 units
Question 5.
A(- 3, 0), B(0, 3), C(3, 0), D(0, – 3)
Answer:
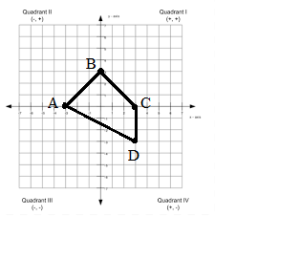
Points:
A(- 3, 0), B(0, 3), C(3, 0), D(0, – 3)
Segments:
AB = 3.5 units
BC = 3.5 units
CD = 3 units
AD = 6 units
Question 6.
A(0, 0), B(4, 0), C(1, 1), D(0, 3)
Answer:
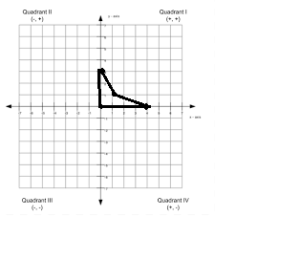
Points:
A(0, 0), B(4, 0), C(1, 1), D(0, 3)
4.1 Translations
Exploration 1
Translating a Triangle in a Coordinate Plane
Work with a partner.
a. Use dynamic geometry software to draw any triangle and label it ∆ABC.
Answer:
b. Copy the triangle and translate (or slide) it to form a new figure, called an image, ∆A’B’C’ (read as triangle A prime, B prime. C prime”).
USING TOOLS STRATEGICALLY
To be proficient in math, you need to use appropriate tools strategically, including dynamic geometry software.
Answer:
c. What is the relationship between the coordinates of the vertices of ∆ABC and
those of ∆A’B’C’?
Answer:
d. What do you observe about the side lengths and angle measures of the two triangles?
Answer:
Exploration 2
Translating a Triangle in a Coordinate Plane
Work with a partner.
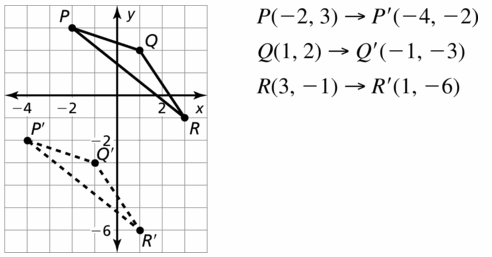
a. The point (x, y) is translated a units horizontally and b units vertically. Write a rule to determine the coordinates of the image of (x, y).
![]()
Answer: (x + a, y + b)
b. Use the rule you wrote in part (a) to translate ∆ABC 4 units left and 3 units down. What are the coordinates of the vertices of the image. ∆A’B’C’?
Answer:
A'(-4, 0), B'(0, 2) and C'(-1, -6)
c. Draw ∆A’B’C.’ Are its side lengths the same as those of ∆ABC? Justify your answer.
Answer:

Exploration 3
Comparing Angles of Translations
Work with a partner.
a. In Exploration 2, is ∆ABC a righL triangle? Justify your answer.
Answer:
b. In Exploration 2, is ∆A’B’C’ a right triangle? Justify your answer.
Answer:
c. Do you think translations always preserve angle measures? Explain your reasoning.
Answer:
Communicate Your Answer
Question 4.
How can you translate a figure in a coordinate plane?
Answer: When you perform translations, you slide a figure left or right, up or down. This means that on the coordinate plane, the coordinates for the vertices of the figure will change. To graph a translation, perform the same change for each point. You can identify a reflection by the changes in its coordinates.
Question 5.
En Exploration 2. translate ∆A’B’C’ 3 units right and 4 units up. What are the coordinates of the vertices of the image, ∆A”B”C”? How are these coordinates
related to the coordinates of the vertices of the original triangle. ∆ABC?
Answer:
Lesson 4.1 Translations
Monitoring Progress
Question 1.
Name the vector and write its component form.
Answer: OA is the vector in the given figure. It is a position vector.
Question 2.
The vertices of ∆LMN are L(2, 2), M(5, 3), and N(9, 1). Translate ∆LMN using the vector (- 2, 6).
Answer:
The vertices of ∆LMN are L(2, 2), M(5, 3), and N(9, 1)
L(2, 2) → L'(0, 8)
M(5, 3) → M'(3, 9)
N(9, 1) → N'(7, 7)
Question 3.
In Example 3. write a rule to translate ∆A’B’C’ back to ∆ABC.
Answer:
Question 4.
Graph ∆RST with vertices R(2, 2), S(5, 2), and T(3, 5) and its image alter the translation (x, y) → (x + 1, y + 2).
Answer:
R(2, 2), S(5, 2), and T(3, 5)
translation (x, y) → (x + 1, y + 2).
x = 2 and y = 2 to find R’
R(2, 2) → (2 + 1, 2 + 2) = R'(3, 4)
S(5, 2) → (5 + 1, 2 + 2) = S'(6, 4)
T(3, 5) → (3 + 1, 5 + 2) = R'(4, 7)
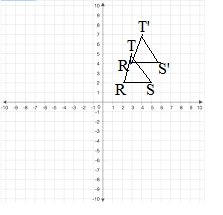
Question 5.
Graph \(\overline{T U}\) with endpoints T(1, 2) and U(4, 6) and its image after the composition.
Translation: (x, y) → (x – 2, y – 3)
Translation: (x, y) → (x – 4, y + 5)
Answer:
Graph \(\overline{T U}\) with endpoints T(1, 2) and U(4, 6) and its image after the composition.
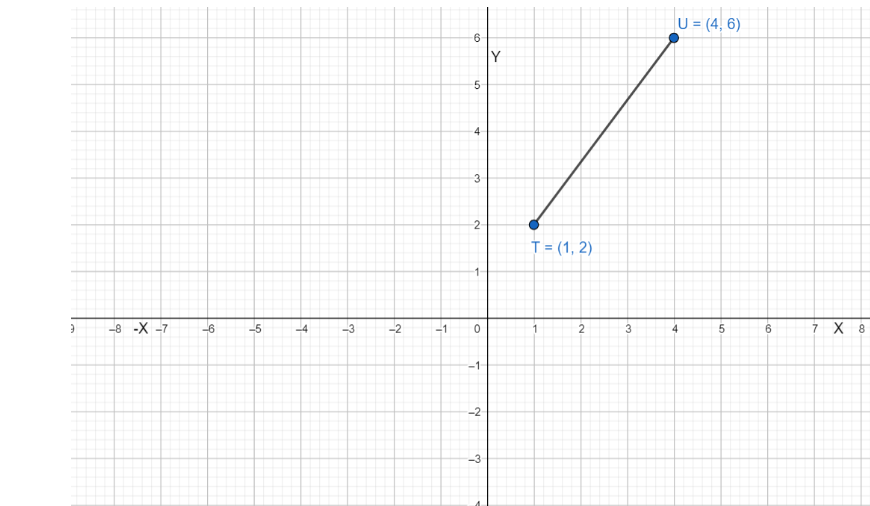
Translation: (x, y) → (x – 2, y – 3)
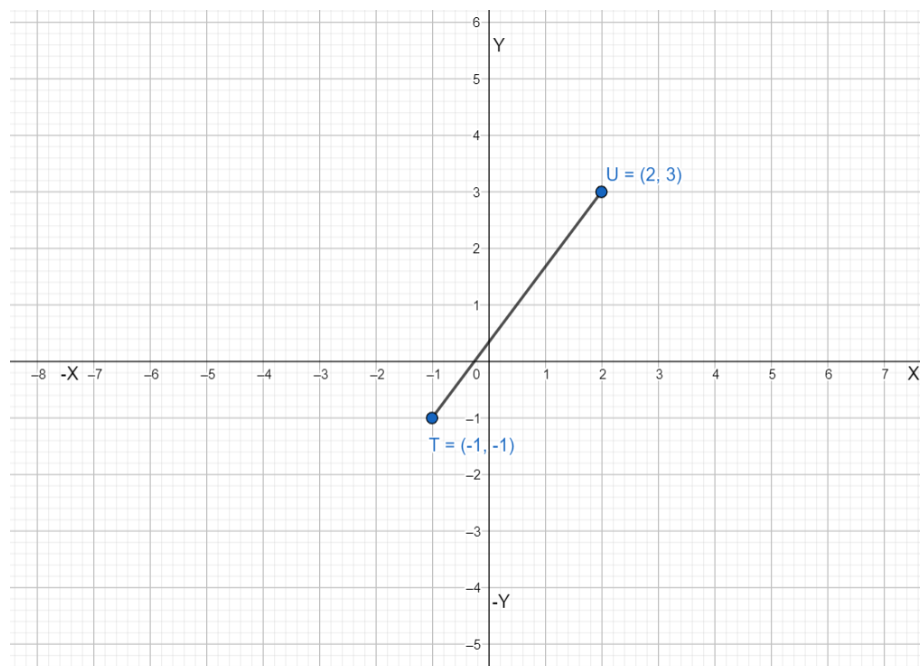
Graph TU and its image after the translation (x, y) → (x – 4, y + 5)
Question 6.
Graph \(\overline{V W}\) with endpoints V(- 6, – 4) and W(- 3, 1) and its image after the composition.
Translation: (x, y) → (x + 3, y + 1)
Translation: (x, y) → (x – 6, y – 4)
Answer:
Graph \(\overline{V W}\) with endpoints V(- 6, – 4) and W(- 3, 1) and its image after the composition.
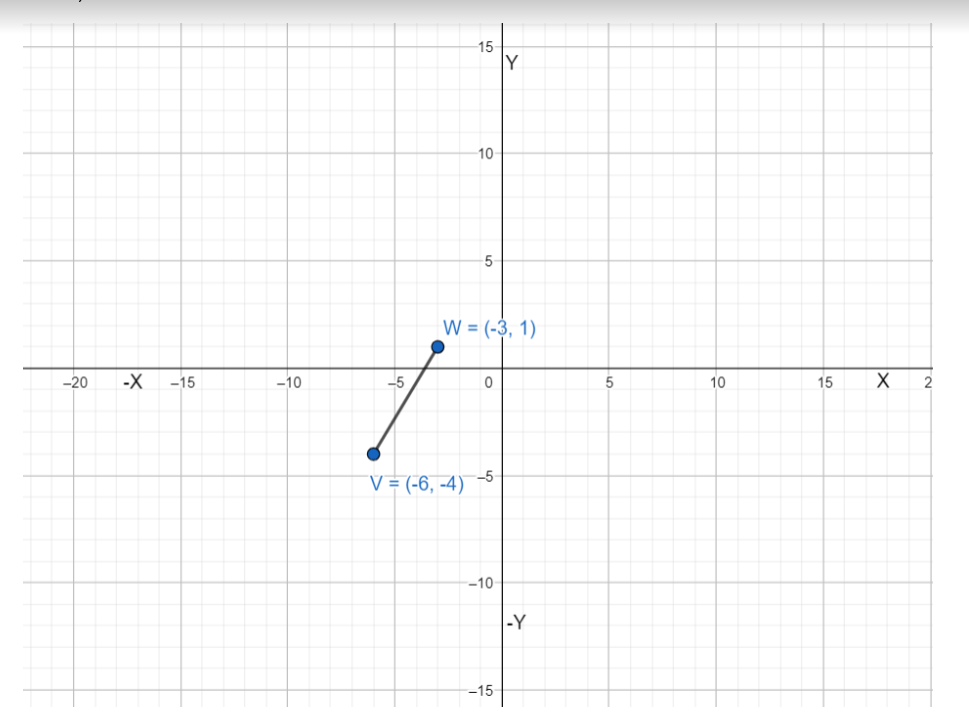
Translation: (x, y) → (x + 3, y + 1)
Translation: (x, y) → (x – 6, y – 4)
Question 7.
In Example 6, you move the gray square 2 units right and 3 units up. Then you move the gray square 1 unit left and 1 unit down. Rewrite the composition as a single transformation.
Answer:
Exercise 4.1 Translations
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Name the preimage and image of the transformation ∆ABC – ∆A’B’C’.
Answer:
∆ABC is the preimage and ∆A’B’C’ is the image.
Question 2.
COMPLETE THE SENTENCE
A _______ moves every point of a figure the same distance in the same direction.
Answer: A translation moves every point of a figure the same distance in the same direction.
Monitoring Progress and Modeling with Mathematics
In Exercises 3 and 4, name the vector and write its component form.
Question 3.
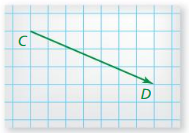
Answer:
![]()
Question 4.
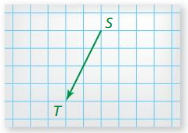
Answer:
A vector is quantity that has both direction and magnitude.
The vertor is ST to more from the initial point S to the terminal point T, you move 2 units left and 4 units down.
So, the component form is (-2, 4)
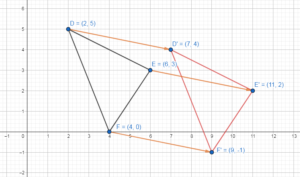
In Exercises 5 – 8, the vertices of ∆DEF are D(2, 5), E(6, 3), and F(4, 0). Translate ∆DEF using the given vector. Graph ∆DEF and its image.
Question 5.
(6, 0)
Answer:
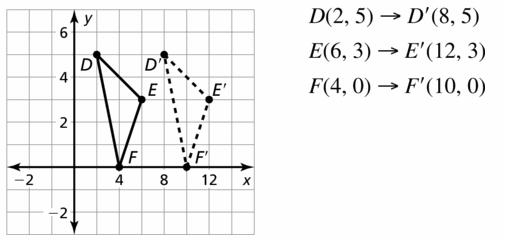
Question 6.
(5, – 1)
Answer:
D(2, 5), E(6, 3) and F(4, 0)
D'(7, 4)
E'(11, 2)
F'(9, -1)
Question 7.
(- 3, – 7)
Answer:
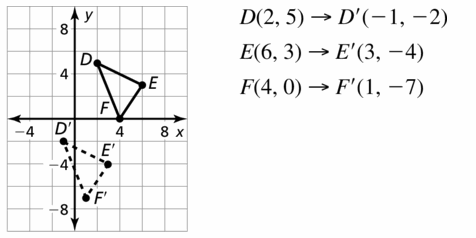
Question 8.
(- 2, – 4)
Answer:
D(2, 5), E(6, 3) and F(4, 0)

D'(0, 1)
E'(4, -1)
F'(2, -4)
In Exercises 9 and 10, find the component form of the vector that translates P(- 3, 6) to P’.
Question 9.
P'(0, 1)
Answer:
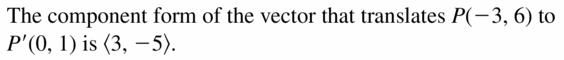
Question 10.
P'(- 4, 8)
Answer:
P(-3, 6) → P'(-3 + x, 6 + y) = P'(- 4, 8)
-3 + x = -4
x = -1
6 + y = 8
y = 8 – 6
y = 2
The component form is (x, y) = (-1, 2)
In Exercises 11 and 12, write a rule for the translation of ∆LMN to ∆L’M’W’.
Question 11.
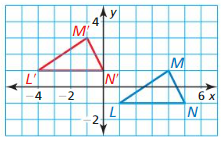
Answer:
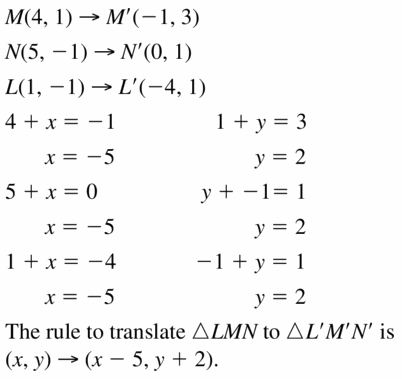
Question 12.
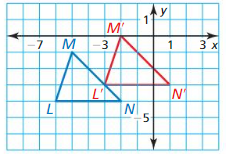
Answer:
To go from M to M’, you move 3 units right and 1 unit up
So you unmove along vector (3, 1)
In Exercises 13 – 16, use the translation.
(x, y) → (x – 8,y + 4)
Question 13.
What is the image of A(2, 6)?
Answer:
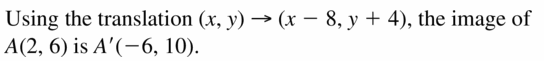
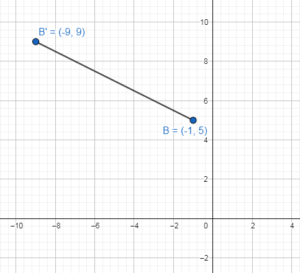
Question 14.
What is the image of B(- 1, 5)?
Answer:
(x, y) → (x – 8,y + 4)
B(- 1, 5)
(-1, 5) → (-1 – 8,5 + 4) = B'(-9, 9)
Question 15.
What is the preimage of C'(- 3, – 10)?
Answer:
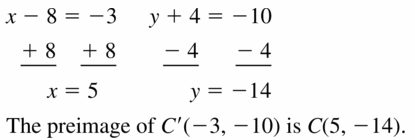
Question 16.
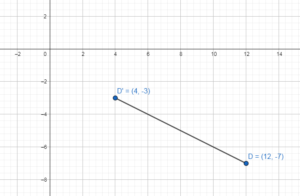
What is the preimage of D'(4, – 3)?
Answer:
(x, y) → (x – 8,y + 4)
D'(4, – 3)
x – 8 = 4
x = 12
y + 4 = -3
y = 7
D(12, 7)
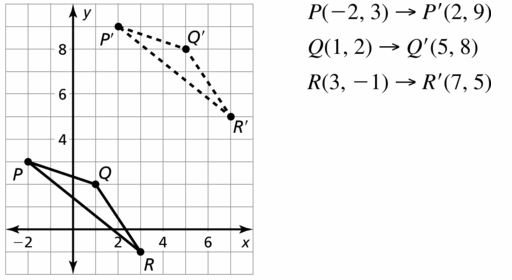
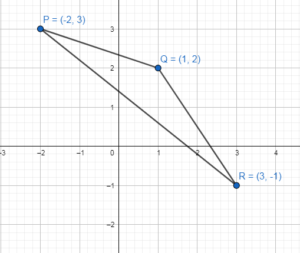
In Exercises 17 – 20, graph ∆PQR with vertices P (-2, 3) Q(1, 2), and R(3, – 1) and its image after the translation.
Question 17.
(x, y) → (x + 4, y + 6)
Answer:
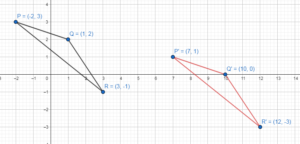
Question 18.
(x, y) → (x + 9, y – 2)
Answer:
P (-2, 3) Q(1, 2), and R(3, – 1)
(x, y) → (x + 9, y – 2)
P'(7, 1)
Q'(10, 0)
R'(12, -3)
Question 19.
(x, y) → (x – 2, y – 5)
Answer:
Question 20.
(x, y) → (x – 1, y + 3)
Answer:
P (-2, 3) Q(1, 2), and R(3, – 1)
translation: (x, y) → (x – 1, y + 3)
(x, y) → (x – 1, y + 3)
x = -2 and y = -3 from point P(-2, 3)
(-2, 3) → (-2 – 1, 3 + 3) = P'(-3, 6)
Q(1, 2) → (1 – 1, 2 + 3) = Q'(0, 5)
R(3, -1) → (3 – 1, -1 + 3) = R'(2, 2)
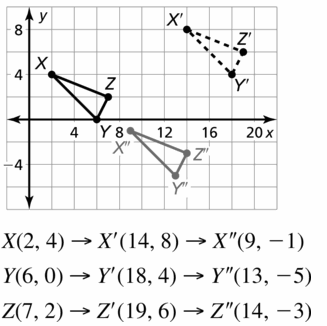
In Exercises 21 and 22. graph ∆XYZ with vertices X(2, 4), Y(6, 0). and Z(7, 2) and its image after the composition.
Question 21.
Translation: (x, y) → (x + 12, y + 4)
Translation: (x, y) → (x – 5, y – 9)
Answer:
Question 22.
Translation: (x, y) → (x – 6, y)
Translation: (x, y) → (x + 2, y + 7)
Answer:
X(2, 4), Y(6, 0). and Z(7, 2)
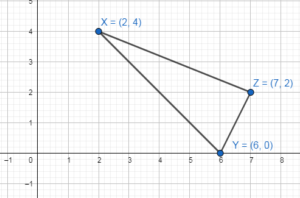
Translation: (x, y) → (x – 6, y)
X(2, 4) → (2 – 6, 4) = X'(-4, 4)
Y(6, 0) → (6 – 6, 0) = Y'(0, 0)
Z(7, 2) → (7 – 6, 2) = Z'(1, 2)
translation: (x, y) → (x + 2, y + 7)
(x, y) → (x + 2, y + 7)
X'(-4, 4) → (-4 + 2, 4 + 7) = X”(-2, 11)
Y'(0, 0) → (0 + 2, 0 + 7) = Y”(2, 7)
Z'(1, 2) → (1 + 2, 2 + 7) = Z”(3, 9)
In Exercises 23 and 24, describe the composition of translations.
Question 23.
Answer:
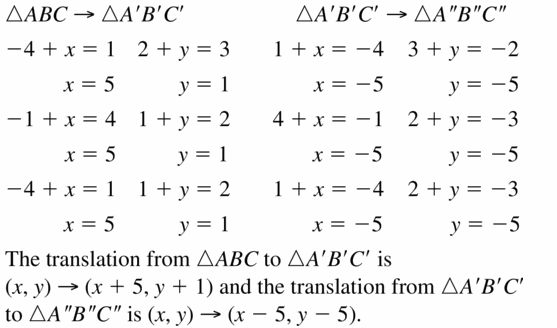
Question 24.
Answer:
vertex 6 units right and 4 units down.
1. translation (x, y) → (x + 6, y – 4)
vertex 6 units left
2. translation (x, y) → (x – 6, y)
Question 25.
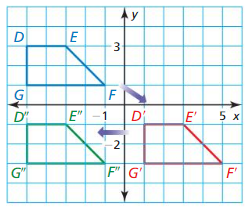
ERROR ANALYSIS
Describe and correct the error in graphing the image of quadrilateral EFGH after the translation (x, y) → (x – 1, y – 2).
Answer:

Question 26.
MODELING WITH MATHEMATICS
In chess, the knight (the piece shaped like a horse) moves in an L pattern. The hoard shows two consecutive moves of a black knight during a game. Write a composition of translations for the moves. Then rewrite the composition as a single translation that moves the knight from its original position to its ending position.

Answer:
Assuming the initial position of the knight is (x, y)
The first translation moved the knight 2 units right and 1 unit down.
The first translation is (x, y) → (x + 2, y – 1)
The second translation moved the knight 1 unit right and 2 unit down.
The first translation is (x, y) → (x + 1, y – 2)
Single translation rule is the sum of both first and second translations
(x, y) → (x + 2 + 1, y – 1 – 2) = (x + 3, y – 3)
Question 27.
PROBLEM SOLVING
You are studying an amoeba through a microscope. Suppose the amoeba moves on a grid-indexed microscope slide in a straight line from square B3 to square G7.
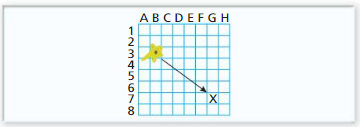
a. Describe the translation.
b. The side length of each grid square is 2 millimeters. How far does the amoeba travel?
c. The amoeba moves from square B3 to square G7 in 24.5 seconds. What is its speed in millimeters per second?
Answer:

Question 28.
MATHEMATICAL CONNECTIONS
Translation A maps (x, y) to (x + n, y + t). Translation B maps (x, y) to (x + s, y + m).
a. Translate a point using Translation A, followed by Translation B. Write an algebraic rule for the final image of the point after this composition.
Answer:
Translation A maps (x, y) to (x + n, y + t)
Translation B maps (x, y) to (x + s, y + m)
Translating a point using translation A followed by translation B.
First: Applying translation A from the initial point (x, y) maps it to the final point (x + n, y + t)
Applying translation B from the initial point (x + n, y + t) maps it to the final point (x + n + s, y + t + m)
The single translation rule for the composition
(x, y) → (x + n + s, y + t + m)
b. Translate a point using Translation B, followed by Translation A. Write an algebraic rule for the final image of the point after this composition.
Answer:
Translating a point using translation A followed by translation B.
First: Applying translation A from the initial point (x, y) maps it to the final point (x + s, y + m)
Applying translation B from the initial point (x + s, y + m) maps it to the final point (x + n + s, y + t + m)
The single translation rule for the composition
(x, y) → (x + n + s, y + t + m)
c. Compare the rules you wrote for parts (a) and (b) Does it matter which translation you do first? Explain your reasoning.
Answer:
Translating a point using translation A followed by translation B is the same as translation using B followed by A.
(x, y) → (x + n + s, y + t + m)
is equivalent to the single rule of the second case
(x, y) → (x + s + n, y + m + t)
MATHEMATICAL CONNECTIONS
In Exercises 29 and 30, a translation maps the blue figure to the red figure. Find the value of each variable.
Question 29.

Answer:
The blue figure is congruent to the red figure.
r = 100 because corresponding angles are congruent.
162 = 3w
w = 54 because corresponding sides are congruent.
2t = 10
t = 5 because corresponding sides are congruent.
s = 8 because corresponding sides are congruent.
Question 30.
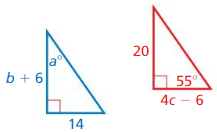
Answer:
Since translation is a rigid motion, then the lengths and angles of the image are the same as the preimage.
a = 180 – 90 – 55
a = 35
b + 6 = 20
b = 20 – 6
b = 14
4c – 6 = 14
4c = 14 + 6
4c = 20
c = 20/4 = 5
c = 5
Question 31.
USING STRUCTURE
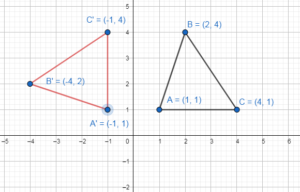
Quadrilateral DEFG has vertices D(- 1, 2), E(- 2, 0), F(- 1, – 1), and G( 1, 3). A translation maps quadrilateral DEFG to quadrilateral D’E’F’G’. The image of D is D'(- 2, – 2). What are the coordinates of E’, F’, and G’?
Answer:

Question 32.
HOW DO YOU SEE IT?
Which two figures represent a translation? Describe the translation.
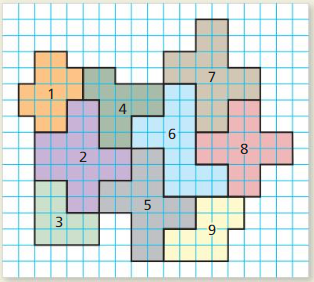
Answer:
To move from figure 5 to figure 7 you must move 4 units right and 8 units up.
Question 33.
REASONING
The translation (x, y) → (x + m, y + n) maps \(\overline{P Q}\) to \(\overline{P’ Q’}\). Write a rule for the translation of \(\overline{P’ Q’}\) to \(\overline{P Q}\). Explain your reasoning.
Answer:
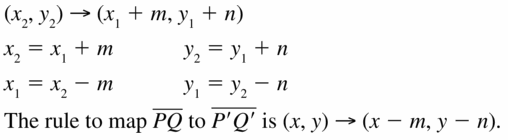
Question 34.
DRAWING CONCLUSIONS
The vertices of a rectangle are Q(2, – 3), R(2, 4), S(5, 4), and T(5, – 3),
a. Translate rectangle QRST 3 units left and 3 units down to produce rectangle Q’R’S’T’. Find the area of rectangle QRST and the area of rectangle Q’R’S’T’.
Answer:
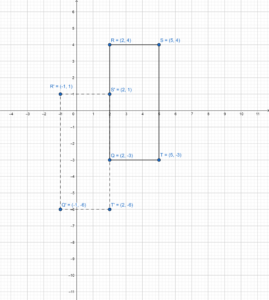
The length of each rectangle = 7 units
Width of each rectangle = 3 units
The area of QRST = 7 × 3 = 21 sq. units
The area of Q’R’S’T’ = 7 × 3 = 21 sq. units
b. Compare the areas. Make a conjecture about the areas of a preimage and its image after a translation.
Answer:
The area of QRST = The area of Q’R’S’T’ = 21 sq. units
Translation creates an image that is congruent to the original figure.
Question 35.
PROVING A THEOREM
Prove the Composition Theorem (Theorem 4.1).
Answer:

Question 36.
PROVING A THEOREM
Use properties of translations to prove each theorem.
a. Corresponding Angles Theorem (Theorem 3. 1)
Answer:
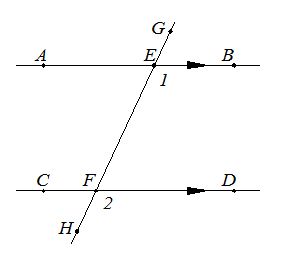
\(\overline{A B}\)|| \(\overline{C D}\)
Using \(\overline{E F}\) a translation vector.
Translating ∠BEF along \(\overline{E F}\) until F becomes the image of E.
\(\overline{E B}\) || \(\overline{E’ B’}\)
So, \(\overline{E’ B’}\) coincides \(\overline{F D}\) as they are parallel and have a common endpoint.
Since translation is a rigid motions.
Then ∠1 ≅ ∠2
Thus, If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
b. Corresponding Angles Converse (Theorem 3.5)
Answer:
Given,
∠AEF ≅ ∠EFD
Assume \(\overline{A B}\) and \(\overline{C D}\) are not parallel.
If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
Question 37.
WRITING
Explain how to use translations to draw a rectangular prism.
Answer:
Question 38.
MATHEMATICAL CONNECTIONS
The vector PQ = (4, 1) describes the translation of A(- 1, w) Onto A'(2x + 1, 4) and B(8y – 1, 1) Onto B'(3, 3z). Find the values of w, x, y, and z.
Answer:
The vector PQ = (4, 1) describes the translation of A(- 1, w) Onto A'(2x + 1, 4) and B(8y – 1, 1) Onto B'(3, 3z).
(-1, w) → (-1 + 4, w + 1) = (3, w + 1)
A'(2x + 1, 4)
(3, w + 1) = (2x + 1, 4)
3 = 2x + 1
2x = 2
x = 1
w + 1 = 4
w = 4 – 1
w = 3
We know that vector PQ = (4, 1) describes the translation of B(8y – 1, 1)
(8y – 1, 1) → (8y – 1 + 4, 1 + 1) = (8y + 3, 2)
B'(3, 3z)
(8y + 3, 2) = (3, 3z)
8y + 3 = 3
8y = 3 – 3
8y = 0
y = 0
3z = 2
z = 2/3
Question 39.
MAKING AN ARGUMENT
A translation maps \(\overline{G H}\) to \(\overline{G’ H’}\). Your friend claims that if you draw segments connecting G to G’ and H to H’, then the resulting quadrilateral is a parallelogram. Is your friend correct? Explain your reasoning.
Answer:

Question 40.
THOUGHT PROVOKING
You are a graphic designer for a company that manufactures floor tiles. Design a floor tile in a coordinate plane. Then use translations to show how the tiles cover an entire floor. Describe the translations that map the original tile to four other tiles.
Answer:
Let the tile by a square of side length of 2 units on a coordinate grid.
If one of its vertex lies at the origin, then its other vertices, in that order are (2, 0), (2, 2) and (0, 2)
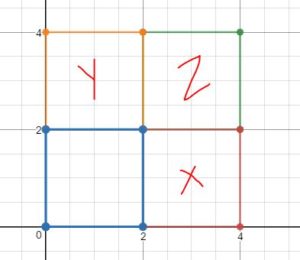
This design can then be used to cover the entire floor by horizontal and vertical translations of 2 units right and upwards.
A horizontal translation of 2 units towards the right maps the tile onto X.
A vertical translation of 2 units upwards maps the tile onto Y and a horizontal translation of Y by 2 units towards the right maps the tile onto Z.
Question 41.
REASONING
The vertices of ∆ABC are A(2, 2), B(4, 2), and C(3, 4). Graph the image of ∆ABC after the transformation (x, y) → (x + y, y). Is this transformation a translation? Explain your reasoning.
Answer:
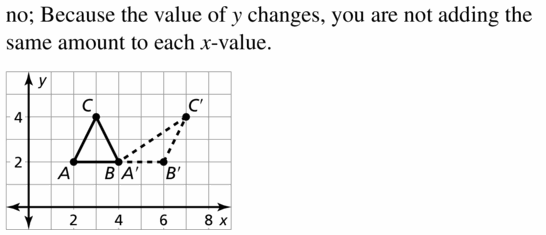
Question 42.
PROOF
\(\overline{M N}\) is perpendicular to line l. \(\overline{M’ N’}\) is the translation of \(\overline{M N}\) 2 units to the left. Prove that \(\overline{M’ N’}\) is perpendicular to l.
Answer:
M’N’ is a horizontal translation of MN by 2 units to the left.
MN and M’N’ are parallel to each other and so their slopes must be equal.
If a line l is perpendicular to MN, then it must be perpendicular to M’N’
Maintaining Mathematical Proficiency
Tell whether the figure can be folded in half so that one side matches the other.
Question 43.

Answer:
Yes; The figure can be folded in half in several ways so that one side matches the other.
Question 44.
Answer: The shape is symmetrical along a diagnol.
Question 45.

Answer:
The shape is asymmetrical
Question 46.
Answer: The shape is symmetrical along its x-axis.
Simplify the expression.
Question 47.
– (- x)
Answer:
When we multiply two negative numbers we get the positive number.
-1 × -x = x
Question 48.
– (x + 3)
Answer:
In this expression minus is multiplied with the whole term
-1 × x + -1 × 3 = -x – 3
Question 49.
x – (12 – 5x)
Answer:
When we multiply two negative numbers we get the positive number.
x – 12 + 5x
Question 50.
x – (- 2x + 4)
Answer:
When we multiply two negative numbers we get the positive number.
x + 2x – 4
4.2 Reflections
Exploration
Reflecting a Triangle Using a Reflective Device
Work with a partner:
Use a straightedge to draw any triangle on paper. Label if ∆ABC.

a. Use the straightedge to draw a line that does not pass through the triangle. Label it m.
Answer:
b. Place a reflective device on line in.
Answer:
c. Use the reflective device to plot the images of the vertices of ∆ABc. Label the images of vertices A, B. and C as A’, B’, and C’, respectively.
Answer:
d. Use a straightedge to draw ∆A’B’C by connecting the vertices.
Answer:
Exploration 2
Reflecting a Triangle in a Coordinate Plane
Work with a partner: Use dynamic geometry software to draw any triangle and label it ∆ABC.
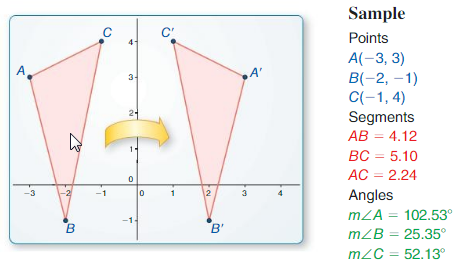
a. Reflect ∆ABC in the y-axis to form ∆A’B’C’.
Answer:
b. What is the relationship between the coordinates of the vertices of ∆ABC and
those of ∆A’B’C’?
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:
c. What do you observe about the side lengths and angle measures of the two triangles?
Answer:
d. Reflect ∆ABC in the x-axis to form ∆A’B’C’. Then repeal parts (b) and (c).
Answer:
Communicate Your Answer
Question 3.
How can you reflect a figure in a coordinate plane?
Answer:
Reflect over the x-axis:
When the figure is reflected over the x-axis. In this case, the axis of reflection is the x-axis.
(x, y) → (x, -y)
Reflect over the y-axis:
When the figure is reflecting over the y-axis, the axis of reflection is the y-axis.
(x, y) → (-x, y)
Lesson 4.2 Reflections
Monitoring progress
Graph ∆ABC from Example 1 and its image after a reflection in the given line.
Question 1.
x = 4
Answer:
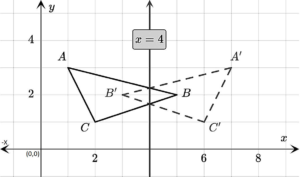
Question 2.
x = – 3
Answer:
Question 3.
y = 2
Answer:
Question 4.
y = – 1
Answer:
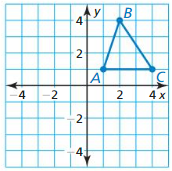
The coordinates of vertices of triangle ABC are A(1, 3), B(5, 2) and C(2, 1)
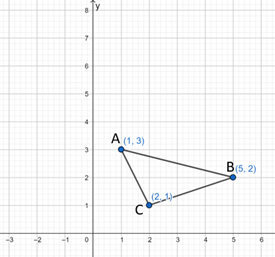
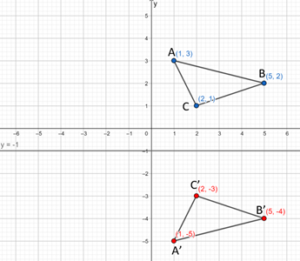
This triangle has its reflection in the line y = -1.
point A is 4 units top of line y = -1, so its reflection A’ is 4 units down at point (1, -5).
Also B’ is 3 units down to the line y = -1 at (5, -4) and C’ is 2 units down from the given line at (2, -3)
Plot the points A'(1, -5), B'(5, -4), C'(2, -3) and join them to form an image of the old triangle.
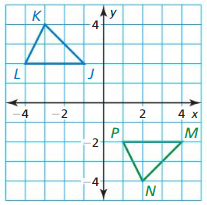
The vertices of ∆JKL are J(1, 3), K(4, 4), and L(3, 1).
Question 5.
Graph ∆JKL and its image after a reflection in the x-axis.
Answer:
Question 6.
Graph ∆JKL and its image after a reflection in the y-axis.
Answer:
Question 7.
Graph ∆JKL and its image after a reflection in the line y = x.
Answer:
Question 8.
Graph ∆JKL and its image aIter a reflection in the line y = – x.
Answer:
Question 9.
In Example 3. verify that \(\overline{F F’}\) is perpendicular to y = – x.
Answer:
Question 10.
WHAT IF?
In Example 4, ∆ABC is translated 4 units down and then reflected in the y-axis. Graph ∆ABC and its image after the glide reflection.
Answer:
Question 11.
In Example 4. describe a glide reflection from ∆A”B”C” to ∆ABC.
Answer:
Determine the number of lines of symmetry for the figure.
Question 12.

Answer:
Given that the figure is a rectangle.
The rectangle has 2 lines of symmetry.
Question 13.
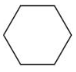
Answer:
Given that the figure is a hexagon.
The hexagon has 6 lines of symmetry.
Question 14.
Answer:
Given that the figure is an equilateral triangle.
The equilateral triangle has 3 lines of symmetry.
Question 15.
Draw a hexagon with no lines of symmetry.
Answer:
You cannot draw a hexagon without lines of symmetry.
A regular hexagon has 6 lines of symmetry. The lines of symmetry is equal to the sides of a figure.
Question 16.
Look back at Example 6. Answer the question by Using a reflection of point A instead of point B.
Answer:
Let us reflect A inline m and draw A’B.
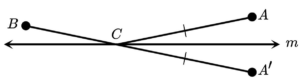
Since A’B is the shortest distance between A’ and B and AC = A’C, they should park at the point C to minimize the combined distance AB + BC.
Exercise 4.2 Reflections
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
A glide reflection is a combination of which two transformations?
Answer:
A glide reflection is a combination of a translation and reflection.
Question 2.
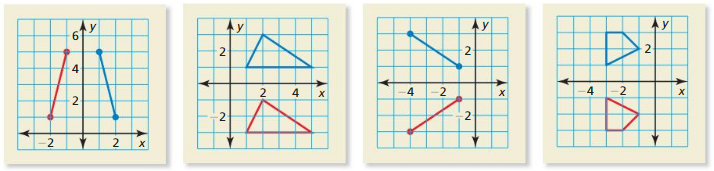
WHICH ONE DOESN’T BELONG?
Which transformation does not belong with the other three? Explain your reasoning.
Answer:
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6, determine whether the coordinate plane shows a reflection in the x-axis, y-axis, or neither.
Question 3.
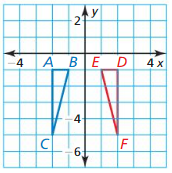
Answer:
Reflection in the y-axis
Question 4.
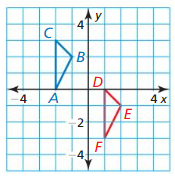
Answer:
We see the triangle ABC with vertices A(-2, 0), B(-1, 2) and C(-2, 3)
We also see the triangle DEF with vertices D(1, 0), E(2, -1) and F(1, -3)
Apply reflection in the x-axis to the triangle ABC, we do not have the points D, E and F in the same place on opposite sides.
Apply reflection in the y-axis to the triangle ABC, we do not have the points D, E and F in the same place on opposite sides.
There is no reflection.
Question 5.
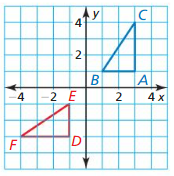
Answer:
We observe the triangles ABC and DEF, we can say that there is no reflection.
Question 6.
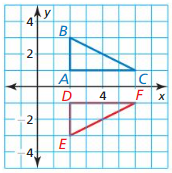
Answer:
The triangle ABC with vertices A(2, 1), B(2, 3) and C(6, 1)
Apply reflection in the x-axis to the triangle ABC.
By seeing the above graph we say that the point which is in the same place on opposite sides x-axis with respect to the point A.
The point is D(2, -1)
By seeing the above graph we say that the point which is in the same place on opposite sides x-axis with respect to the point B.
The point is E(2, -3)
By seeing the above graph we say that the point which is in the same place on opposite sides x-axis with respect to the point C.
The point is F(6, -1)
We see that the triangle DEF with vertices D(2, -1), E(2, -3) and F(6, -1).
When we apply reflection in the y-axis to the triangle ABC, we do not have the points D, E, F in the same place on opposite sides.
In Exercises 7 – 12, graph ∆JKL and its image after a reflection in the given line.
Question 7.
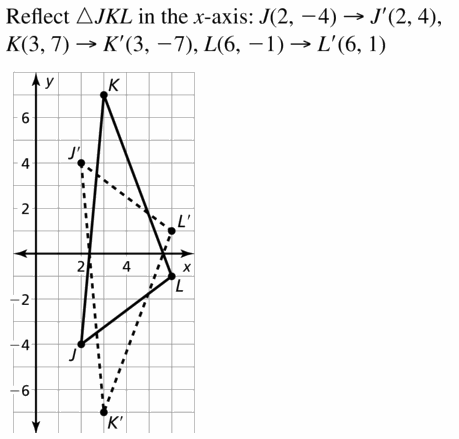
J(2, – 4), K(3, 7), L(6, – 1); x-axis
Answer:
Question 8.
J(5, 3), K(1, – 2), L(- 3, 4); y-axis
Answer:
J(5, 3), K(1, – 2), L(- 3, 4)
We will apply reflection in the y-axis to the triangle JKL.
J’ which is in the same place on opposite sides y-axis with respect to the point J(5, 3)
The coordinates of this point are J'(-5, 3)
K’ which is in the same place on opposite sides y-axis with respect to the point K(1, -2)
The coordinates of this point are K'(-1, -2)
L’ which is in the same place on opposite sides y-axis with respect to the point L(-3, 4)
The coordinates of this point are L'(3, 4)
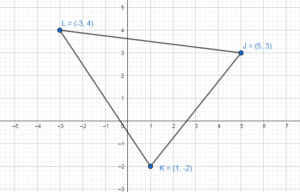
Question 9.
J(2, – 1), K(4, – 5), L(3, 1); x = – 1
Answer:
Question 10.
J(1, – 1), K(3, 0), L(0, – 4); x = 2
Answer:
Apply reflection in the line x = 2 to the triangle JKL.
J = (1, -1) J’ = (3, -1)
K = (3, 0) K’= (1, 0)
L(0, – 4) L’ = (4, -4)
Question 11.
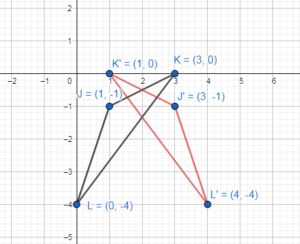
J(2, 4), K(- 4, – 2), L(- 1, 0); y = 1
Answer:
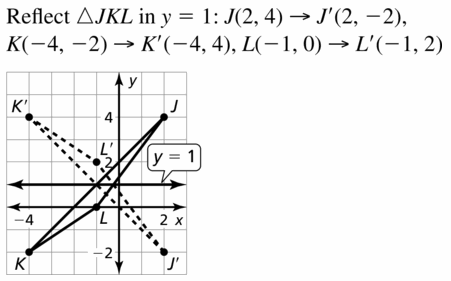
Question 12.
J(3, – 5), K(4, – 1), L(0, – 3); y = – 3
Answer:
Graph the triangle by using the given vertices J(3, – 5), K(4, – 1), L(0, – 3)
J(3, – 5) → J'(3, -1)
K(4, – 1) → K'(4, -5)
L(0, – 3) → L'(0, 3)
In Exercises 13-16, graph the polygon and its image after a reflection in the given line.
Question 13.
y = x
Answer:
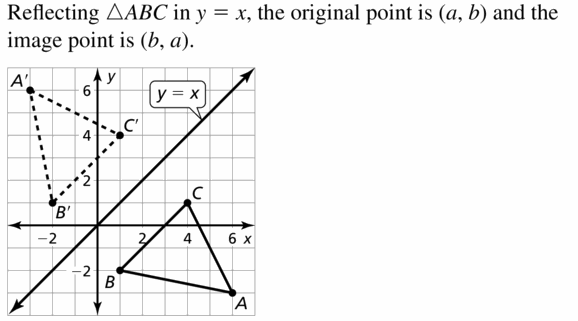
Question 14.
y = x
Answer:
The vertices of the above polygon are A(2, -1), B(-1, 2), C(2, 3) and D(4, 2)
Apply reflection in the line y = x to the polygon ABCD.
So, A'(-1, 2)
B(-1, 2) → B'(2, -1)
C(2, 3) → C'(3, 2)
D(4, 2) → D'(2, 4)
When the point is reflected in the line y = x the coordinates of the point image change place.
Point A’ and B have the same coordinates, and points A and B have the same coordinates.
Question 15.
y = -x
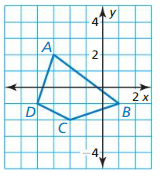
Answer:
Question 16.
y = -x
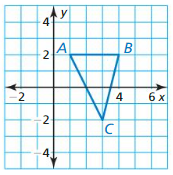
Answer:
Apply reflection in the line y = x to the triangle ABC.
The vertices are A(1, 2), B(4, 2), C(3, -2)
A(1, 2) → A'(-2, -1)
B(4, 2) → B'(-2, -4)
C(3, -2) → C'(2, -3)
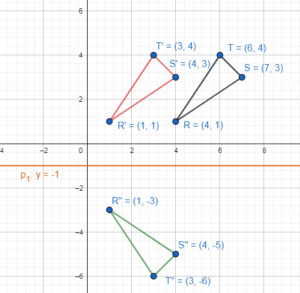
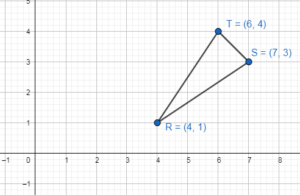
In Exercises 17-20. graph ∆RST with vertices R(4, 1), s(7, 3), and T(6, 4) and its image after the glide reflection.
Question 17.
Translation: (x, y) → (x, y – 1)
Reflection: in the y-axis
Answer:
Question 18.
Translation: (x, y) → (x – 3,y)
Reflection: in the line y = – 1
Answer:
Translation: (x, y) → (x – 3,y)
R(4, 1) to find R’
(4, 1) → (4 – 3,1) = R'(1, 1)
S(7, 3) to find S’
(7, 3) → (7 – 3,3) = S'(4, 3)
T(6, 4) to find T’
(6, 4) → (6 – 3,4) = T'(3, 4)
Apply reflection in the line y = -1 to the triangle R’S’T’
R'(1, 1) → R”(1, -3)
S'(4, 3) → S”(4, -5)
T'(3, 4) → T”(3, -6)
Question 19.
Translation: (x, y) → (x, y + 4)
Reflection: in the line x = 3
Answer:

Question 20.
Translation: (x, y) → (x + 2, y + 2),
Reflection: in the line y = x
Answer:
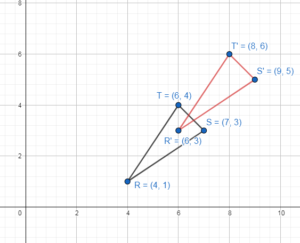
Translation: (x, y) → (x + 2, y + 2),
R(4, 1) to find R’
(4, 1) → (4 + 2,1 + 2) = R'(6, 3)
S(7, 3) to find S’
(7, 3) → (7 + 2,3 + 2) = S'(9, 5)
T(6, 4) to find T’
(6, 4) → (6 + 2,4 + 2) = T'(8, 6)
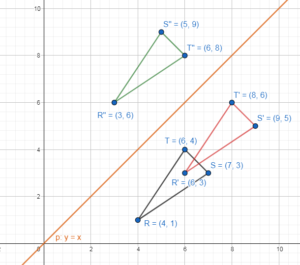
R'(6, 3) → R”(3, 6)
S'(9, 5) → S”(5, 9)
T'(8, 6) → T”(6, 8)
In Exercises 21 – 24, determine the number of lines of symmetry for the figure.
Question 21.

Answer:
Question 22.

Answer:
The figure has 4 lines of symmetry.
Question 23.

Answer:
There are no lines of symmetry.
Question 24.

Answer: The figure has 5 lines of symmetry.
Question 25.
USING STRUCTURE
Identify the line symmetry (if any) of each word.
a. LOOK
b. MOM
c. OX
d. DAD
Answer:

Question 26.
ERROR ANALYSIS
Describe and correct the error in describing the transformation.
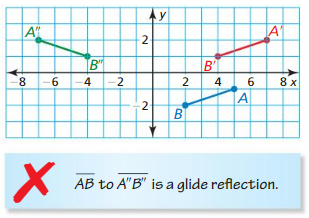
Answer:
By drawing \(\overline{A B}\)
A(5, -1) and B(2, -2)
A(5, -1) → A'(7, 2)
B(2, -2) → B'(4, 1)
Translating \(\overline{A B}\) with the rule (x, y) → (x + 2, y + 3)
Reflecting \(\overline{A’ B’}\) over the y-axis
A'(7, 2) → A”(-7, 2)
B'(4, 1) → B”(-4, 1)
Thus the transformation is a glide reflection.
Question 27.
MODELING WITH MATHEMATICS
You park at some point K on line n. You deliver a pizza to House H, go back to your car. and deliver a pizza to House J. Assuming that you can cut across both lawns, how can you determine the parking location K that minimizes the distance HK + KJ?

Answer:
Reflect H in line n to obtain H’. Connect H’ to J to draw \(\overline{J H’}\).
Label the intersection of JH’ and n as K. Because JH’ is the shortest distance between J and H’ and HK = H’K, park at point K.
Question 28.
ATTENDING TO PRECISION
Use the numbers and symbols to create the glide reflection resulting in the image shown.

Answer:
We will find the preimage of point A”(5, 6)
That is point A'(6, 5)
We will find the preimage of point B”(4, 2)
That is point B'(2, 4)
We will find the preimage of point C”(-1, 5)
That is point C'(5, -1)
Translation is: (x, y) → (x + 3, y + 3)
A(3, 2) in the translation to find A’
(x, y) → (x + 3, y + 3)
(3, 2) → (3 + 3, 2 + 3) = (6, 5)
B(-1, 1) in the translation to find B’
(x, y) → (x + 3, y + 3)
(-1, 1) → (-1 + 3, 1 + 3) = (2, 4)
C(2, -4) in the translation to find C’
(x, y) → (x + 3, y + 3)
(2, -4) → (2 + 3, -4 + 3) = (5, -1)
In Exercises 29 – 32, find point C on the x-axis so AC + BC is a minimum.
Question 29.
A(1, 4), B(6, 1)
Answer:

Question 30.
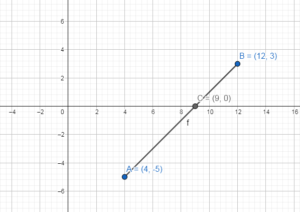
A(4, – 5), B(12, 3)
Answer:
Given,
A(4, – 5), B(12, 3)
We have to find the point C on the x-axis.
Ac + BC is minimum.
First we will plot points in the coordinate system.
The shortest distance from point A to point B gives the line that join these two points.
The line intersects the x-axis at point C.
x = 9 and y = 0
Question 31.
A(- 8, 4), B(- 1, 3)
Answer:

Question 32.
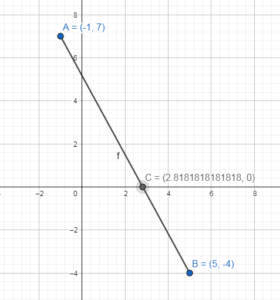
A(- 1, 7), B(5, – 4)
Answer:
A(- 1, 7), B(5, – 4)
We have to find the point C on the x-axis.
AC + BC is minimum.
First we will plot points in the coordinate system.
The shortest distance from point A to point B gives the line that join these two points.
The line intersects the x-axis at point C.
x = 2.8 and y = 0
Question 33.
MATHEMATICAL CONNECTIONS
The line y = 3x + 2 is reflected in the line y = – 1. What is the equation of the image?
Answer:

Question 34.
HOW DO YOU SEE IT?
Use Figure A.
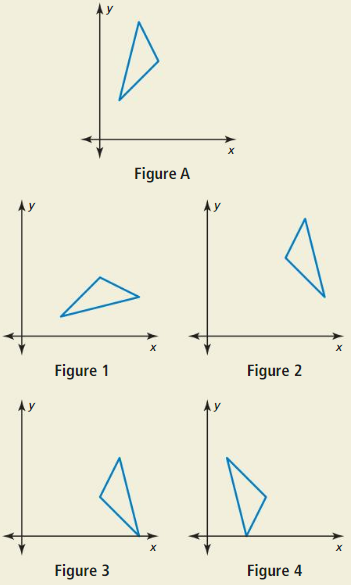
a. Which figure is a reflection of Figure A in the line x = a? Explain.
Answer:
The reflection of Figure A in the line x =a is Fig 2.
Points of Fig 2 is in the same place on opposite sides x = a with respect to the points of Fig A.
b. Which figure is a reflection of Figure A in the line y = b? Explain.
Answer:
The reflection of Figure A in the line y = b is Fig 4.
Points of Fig 4 is in the same place on opposite sides y = b with respect to the points of Fig A.
c. Which figure is a reflection of Figure A in the line y = x? Explain.
Answer:
The reflection of Figure A in the line y = x is Fig 1.
Points of Fig 1 is in the same place on opposite sides y = x-axis with respect to the points of Fig A.
d. Is there a figure that represents a glide reflection? Explain your reasoning.
Answer: The figure that represent glide reflection is Fig 4.
Question 35.
CONSTRUCTION
Follow these steps to construct a reflection of △ ABC in line m. Use a compass and straightedge.
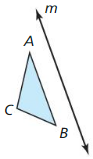
Step 1 Draw △ABC and line m.
Step 2 Use one compass setting to find two points that are equidistant from A on line m. Use the same compass setting to find a point on the other side of m that is the same distance from these two points. Label that point as A’.
Step 3 Repeat Step 2 to find points B’ and C’.
Draw △A’B’C.
Answer:
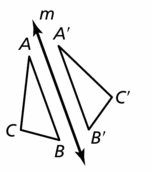
Question 36.
USING TOOLS
Use a reflective device to verify your construction in Exercise 35.
Answer:
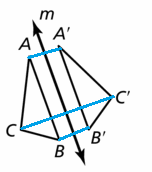
Question 37.
MATHEMATICAL CONNECTIONS
Reflect △MNQ in the line y = -2x.
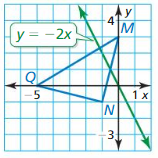
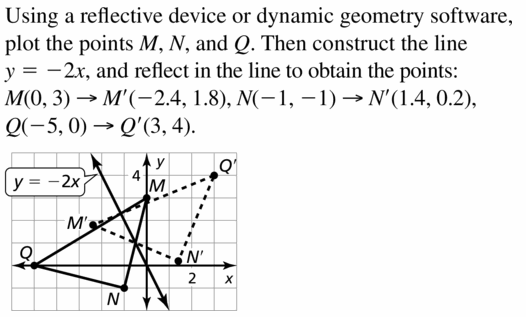
Answer:
Question 38.
THOUGHT PROVOKING
Is the composition of a translation and a reflection commutative? (In other words, do you obtain the same image regardless of the order in which you perform the transformations?) Justify your answer.
Answer:
When the direction of the translation is parallel to the line of reflection, that is only case when the composition of a translation and a reflection is commutative.
Question 39.
MATHEMATICAL CONNECTIONS
Point B (1, 4) is the image of B(3, 2) after a reflection in line c. Write an equation for line c.
Answer:
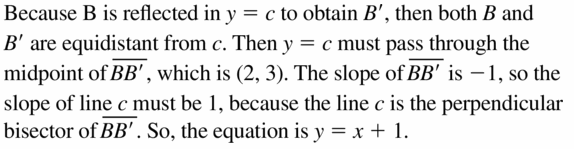
Maintaining Mathematical Proficiency
Use the diagram to Íind the angle measure.
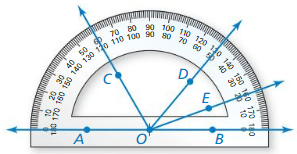
Question 40.
m∠AOC
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠AOC = 60°
Question 41.
m∠AOD
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠AOD = 130°
Question 42.
m∠BOE
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠BOE = 20°
Question 43.
m∠AOE
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠AOE = 160°
Question 44.
m∠COD
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠COD = 70°
Question 45.
m∠EOD
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠EOD = 30°
Question 46.
m∠COE
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠COE = 100°
Question 47.
m∠AOB
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠AOB = 180°
Question 48.
m∠COB
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠COB = 120°
Question 49.
m∠BOD
Answer:
Place the center of the protractor at point O parallel to the longer AB, and then read the measure of the angle from the protractor.
m∠BOD = 50°
4.3 Rotations
Exploration 1
Rotating a Triangle in a Coordinate Plane
Work with a partner:
a. Use dynamic geometry software to draw any triangle and label it ∆ABC.
Answer:
b. Rotate the triangle 90° counterclockwise about the origin to from ∆A’B’C’.
Answer:
c. What is the relationship between the coordinates of the vertices of ∆ABC and those of ∆A’B’C’?
Answer:
d. What do you observe about the side lengths and angle measures of the two triangles?
Answer:
Exploration 2
Rotating a Triangle in a Coordinate Plane
Work with a partner:
a. The point (x, y) is rotated 90° counterclockwise about the origin. Write a rule to determine the coordinates of the image of (x, y).
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to use previous established results in constructing arguments.
Answer:
b. Use the rule you wrote in part (a) to rotate ∆ABC 90° counterclockwise about the origin. What are the coordinates of the vertices of the image. ∆A’B’C’?
Answer:
c. Draw ∆A’B’C’. Are its side lengths the same as those of ∆ABC? Justify your answer.
Answer:
Exploration 3
Rotating a Triangle in a Coordinate Plane
Work with a partner.
a. The point (x, y) is rotated 180° counterclockwise about the origin. Write a rule to
determine the coordinates of the image of (x, y). Explain how you found the rule.
Answer:
b. Use the rule you wrote in part (a) to rotate ∆ABC (front Exploration 2) 180° counterclockwise about the origin. What are the coordinates of the vertices of the image, ∆A’B’C’?
Answer:
Communicate Your Answer
Question 4.
How can you rotate a figure in a coordinate plane?
Answer:
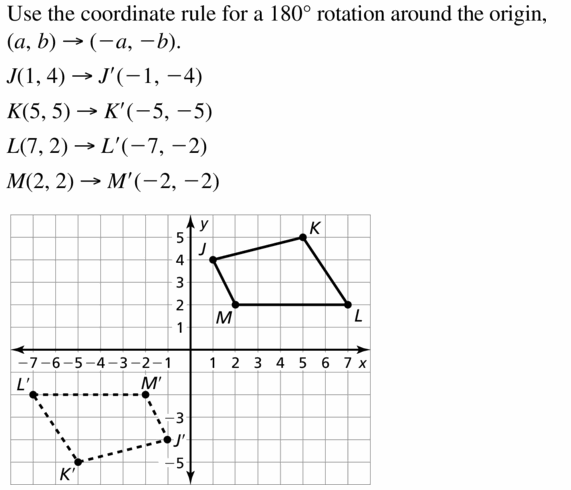
Rotation of a figure at 90° clockwise is given by,
(x, y) = (y, -x)
Rotation of a figure at 180° clockwise is given by,
(x, y) = (-x, -y)
Rotation of a figure at 270° clockwise is given by,
(x, y) = (-y, x)
Rotation of a figure at 90° counterclockwise is given by,
(x, y) = (-y, x)
Rotation of a figure at 180° counterclockwise is given by,
(x, y) = (-x, -y)
Rotation of a figure at 270° counterclockwise is given by,
(x, y) = (y, -x)
Question 5.
In Exploration 3. rotate A’B’C’ 180° counterclockwise about the origin. What are the coordinates of the vertices of the image. ∆A”B”C”? How are these coordinates related to the coordinates of the vertices of the original triangle, ∆ABC?
Answer:
The rotation by angle 180° counterclockwise around the axis is ∆A”B”C” is given as
A”(x, y) = (0, 3)
B”(x, y) = (4, 5)
C”(x, y) = (3, -3)
The coordinates of ∆A”B”C” are the same as the coordinates of ∆ABC, it is 360° rotation.
∆ABC = ∆A’B’C’ = ∆A”B”C”
Lesson 4.3 Rotations
Monitoring Progress
Question 1.
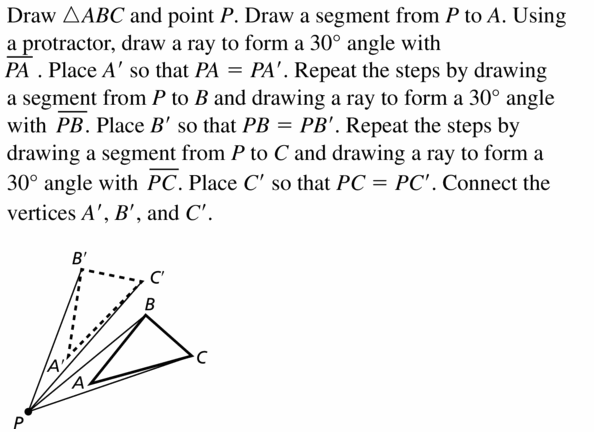
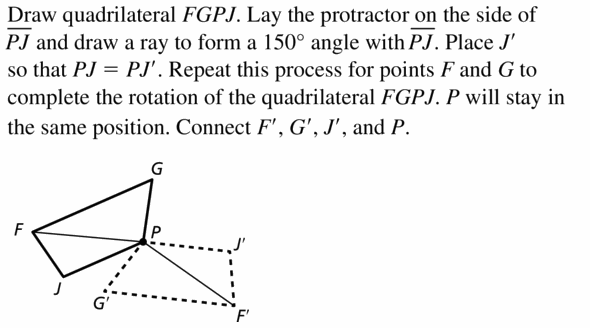
Trace ∆DEF and point P. Then draw a 50° rotation of ∆DEF about point P.
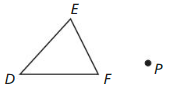
Answer:
First, a segment is drawn between any of the vertices of ∆DEF and point P, starting with point F.
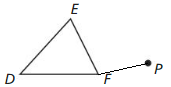
Then using a protractor, a ray is drawn which makes of angle of 50° with PF.
Question 2.
Graph ∆JKL with vertices J(3, 0), K(4, 3), and L(6, 0) and its image after a 90° rotation about the origin.
Answer:
Graph ∆JKL with vertices J(3, 0), K(4, 3), and L(6, 0) and its image after a 90° rotation about the origin.
The rotation of the point of a preimage (x,y) by 90 degrees clockwise gives the point of the image after rotation as (y, -x)
The rotation of point J(3, 0) by 90° clockwise gives J'(0, -3)
The rotation of point K(4, 3) by 90° clockwise gives K'(3, -4)
The rotation of point L(6, 0) by 90° clockwise gives L'(6, 0)
The new coordinates of the triangle J’K’L’ are J'(0, 3), K'(3, -4), and L'(6, 0)
Question 3.
Graph \(\overline{R S}\) from Example 3. Perform the rotation first, followed by the reflection. Does the order of the transformations matter? Explain.
Answer:
Question 4.
WHAT IF?
In Example 3. \(\overline{R S}\) is reflected in the x-axis and rotated 180° about the origin. Graph \(\overline{R S}\) and its image after the composition.
Answer:
Question 5.
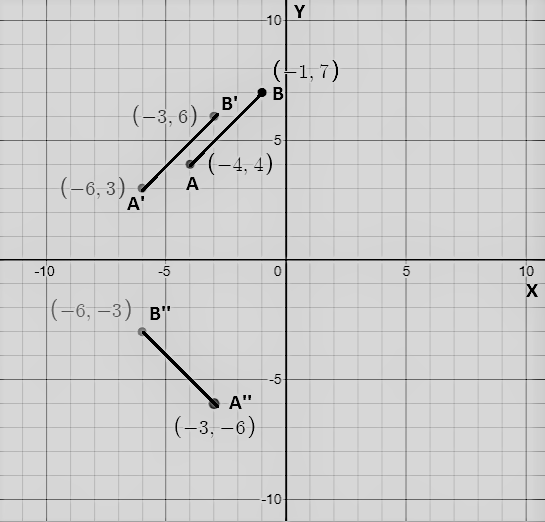
Graph \(\overline{A B}\) with endpoints A(- 4, 4) and B(- 1, 7) and its image after the composition.
Translation: (x, y) → (x – 2, y – 1)
Rotation: 90° about the origin
Answer:
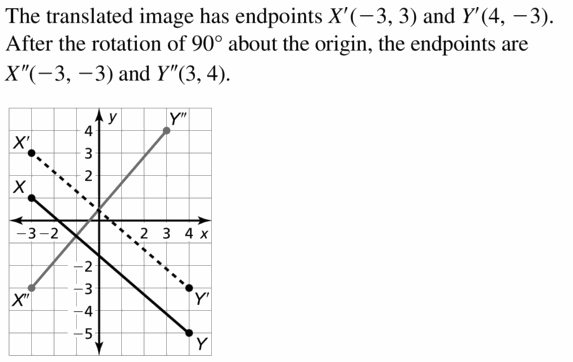
Given,
Graph \(\overline{A B}\) with endpoints A(- 4, 4) and B(- 1, 7) and its image after the composition.
Translation: (x, y) → (x – 2, y – 1)
Rotation: 90° about the origin
A'(-4 – 2, 4 – 1) = (-6, 3)
B'(-1 – 2, 7 – 1) = (-3, 6)
Rotate \(\overline{A’ B’}\) 90° about the origin A”B” has end points A”(-3, -6), B”(-6, -3)
Question 6.
Graph ∆TUV with vertices T(1, 2), U(3. 5), and V(6, 3) and its image after the composition.
Rotation: 180° about the origin
Reflection: in the x-axis
Answer:
We know that the image of (a, b) after a rotation of 180° about the origin is given as (-a, -b)
T(1, 2) = T(-1, -2)
U(3, 5) = U'(-3, -5)
V(6, 3) = V'(-6, -3)
T'(-1, 2) = T”(-1, 2)
U'(-3, -5) = U”(-3, 5)
V'(-6, -3) = V(-6, 3)
Determine whether the figure has rotational symmetry. If so, describe any rotations that map the figure onto itself.
Question 7.
rhombus
Answer:
So within 360∘ rhombus turns 2 times into itself as 360∘ divided by 180∘ is 2.
Hence the order of rotational symmetry of the rhombus is 2.
Question 8.
octagon

Answer:
A regular octagon has 8 lines of symmetry and a rotational symmetry of order 8. This means that it can be rotated in such a way that it will look the same as the original shape 8 times in 360°.
Question 9.
right triangle
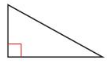
Answer: A right triangle does not have rotational symmetry.
Exercise 4.3 Rotations
Vocabulary and Core Concept Check
Question 1.
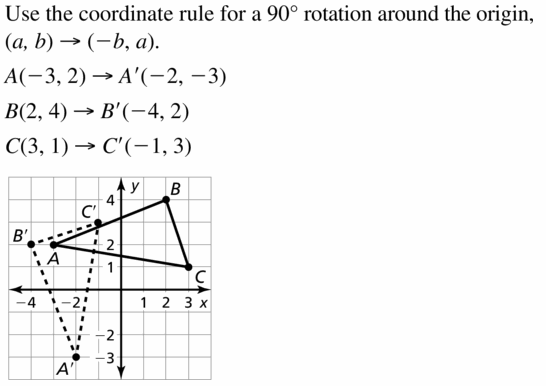
COMPLETE THE SENTENCE
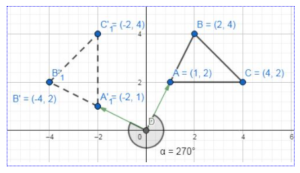
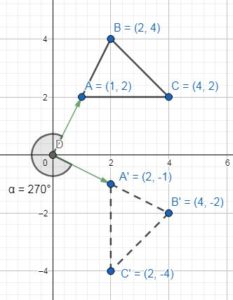
When a point (a, b) is rotated counterclockwise about the origin. (a, b) → (b, – a) is the result of a rotation of _________ .
Answer:
When a point (a, b) is rotated counterclockwise about the origin. (a, b) → (b, – a) is the result of a rotation of 270°
Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.
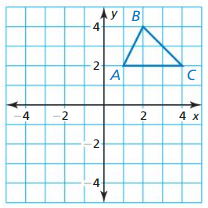
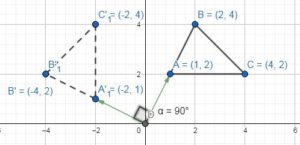
What are the coordinates of the vertices of the image after a 90° counterclockwise rotation about the origin?
Answer:
When rotating the figure 90° counterclockwise the coordinates will be
A(1, 2) → A'(-2, 1)
B(2, 4) → B'(-4, 2)
C(4, 2) → C'(-2, 4)
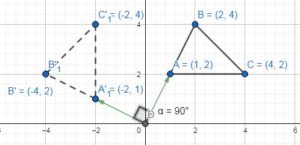
What are the coordinates of the vertices of the image after a 270° clockwise rotation about the origin?
Answer:
When rotating the figure 270° counterclockwise the coordinates will be
A(1, 2) → A'(-2, 1)
B(2, 4) → B'(-4, 2)
C(4, 2) → C'(-2, 4)
What are the coordinates of the vertices of the image after turning the figure 90° to the left about the origin?
Answer:
Rotating 90° to the left is equivalent to rotating the figure 90° counterclockwise the coordinates will be
A(1, 2) → A'(-2, 1)
B(2, 4) → B'(-4, 2)
C(4, 2) → C'(-2, 4)
What are the coordinates of the vertices of the image after a 270° counterclockwise rotation about the origin?
Answer:
When rotating the figure 270°clockwise the coordinates will be
A(1, 2) → A'(-2, 1)
B(2, 4) → B'(-4, 2)
C(4, 2) → C'(-2, 4)
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6. trace the polygon and point P. Then draw a rotation o the polygon about point P using the given number of degrees.
Question 3.
30°
Answer:
Question 4.
80°
Answer:
Question 5.
150°
Answer:
Question 6.
130°
Answer:

In Exercises 7-10. graph the polygon and its image after a rotation of the given number of degrees about the origin.
Question 7.
90°
Answer:
Question 8.
180°
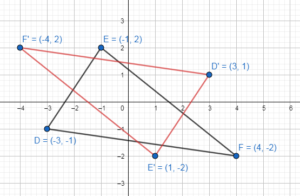
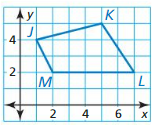
Answer:
The vertices of DEF are D(-3, -1), E(-1, 2) and F(4, -2)
Rotate D(-3, -1) through an angle 180° about the origin, we will get the point D'(3, 1)
Rotate E(-1, 2) through an angle 180° about the origin, we will get the point E'(1, -2)
Rotate F(4, -2) through an angle 180° about the origin, we will get the point F'(-4, 2)
We will rotate the point of triangle through an angle 180° about the origin, the coordinates of the point image change sign.
Then we will graph the triangle D’E’F’ with vertices D'(3, 1), E'(1, -2) and F'(-4, 2)
Question 9.
180°
Answer:
Question 10.
270°
Answer:
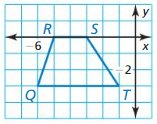
Rotation 270°
Q(-6, -3) → Q'(-3, 6)
R(-5, 0) → R'(0, 5)
S(-3, 0) → S'(0, 3)
T(-1, -3) → T'(-3, 1)
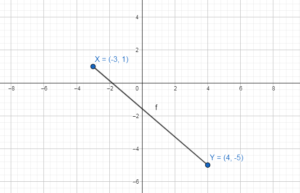
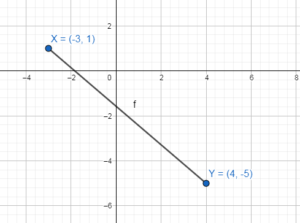
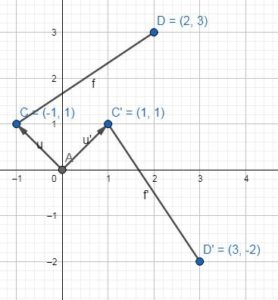
In Exercises 11-14, graph \(\overline{X Y}\) with endpoints X(-3, 1) and Y(4, – 5) and its image after the composition.
Question 11.
Translation: (x, y) → (x, y + 2)
Rotation: 90° about the origin
Answer:
Question 12.
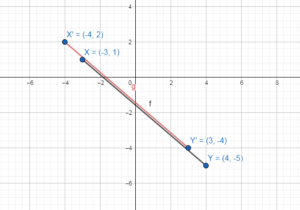
Rotation: 180° about the origin
Translation: (x, y) → (x – 1, y + 1)
Answer:
X(-3, 1) and Y(4, -5)
Translation: (x, y) → (x – 1, y + 1)
x = -3 and y = 1 in the translation to find X’
(x, y) → (x – 1, y + 1)
(-3, 1) → (-3 – 1, 1 + 1) = (-4, 2)
x = 4 and y = -5 in the translation to find Y’
(x, y) → (x – 1, y + 1)
(4, -5) → (4 – 1, -5 + 1) = (3, -4)
X'(-4, 2) and Y'(3, -4)
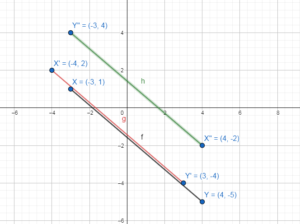
Rotate 180° about the origin
X'(-4, 2) = X”(4, -2)
Y'(3, -4) = Y”(-3, 4)
X”(4, -2) and Y”(-3, 4)
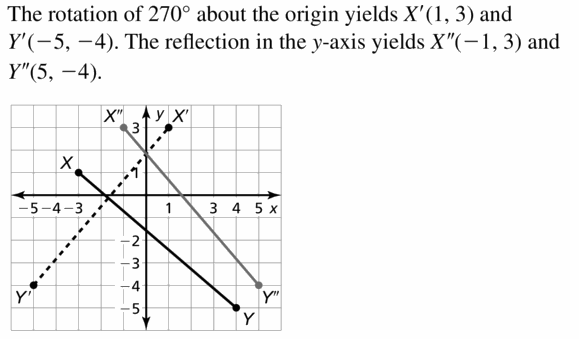
Question 13.
Rotation: 270° about the origin
Reflection: in the y-axis
Answer:
Question 14.
Reflection: in the line y = x
Rotation: 180° about the origin
Answer:
X(-3, 1) and Y(4, -5)
Reflection in the line y = x to the \(\overline{X Y}\)
X'(1, -3)
Y'(-5, 4)
\(\overline{X’ Y’}\) with end points X'(1, -3) and Y'(-5, 4)
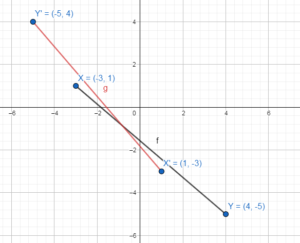
Rotate X'(1, -3) through an angle 180° we get X”(-1, 3)
Rotate Y'(-5, 4) through an angle 180° we get Y”(5, -4)
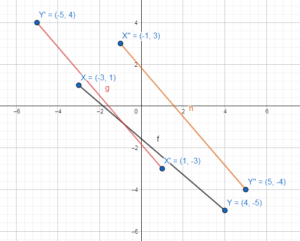
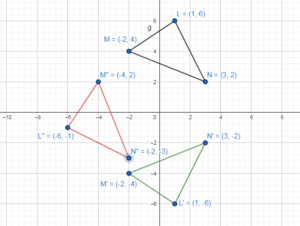
In Exercises 15 and 16, graph ∆LMN with vertices 2 L(1, 6), M(- 2, 4), and N(3, 2) and its image after the composition.
Question 15.
Rotation: 90° about the origin
Translation: (x, y) → (x – 3, y + 2)
Answer:
Question 16.
Reflection: in the x-axis
Rotation: 270° about the origin
Answer:
The vertices are L(1, 6), M(-2, 4) and N(3, 2)
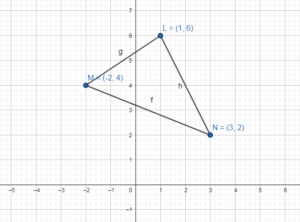
L’ which is in the same place on opposite sides x-axis with respect to the point L(1, 6).
The coordinates of this point are L'(1, -6)
M’ which is in the same place on opposite sides x-axis with respect to the point M(-2, 4).
The coordinates of this point are M'(-2, -4)
N’ which is in the same place on opposite sides x-axis with respect to the point N(3, 2).
The coordinates of this point are N'(3, -2)
L'(1, -6), M'(-2, -4) and N'(3, -2)
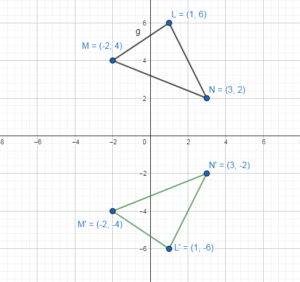
L'(1, -6) → L”(-6, -1)
M'(-2, -4) → M”(-4, 2)
N'(3, -2) → N”(-2, -3)
In Exercises 17-20, determine whether the figure has rotational symmetry. If so, describe any rotations that map the figure onto itself.
Question 17.
Answer:
The rotations of 90° and 180° about the center will map this figure onto itself.
Question 18.

Answer:
The figure has rotational symmetry.
The rotation center is the center of the shape.
Rotation of 72°, 144°, 216°, 288° and 360° about the center all map the shape onto itself.
Question 19.

Answer:
The rotations of 45°, 90°, 135° and 180° about the center will map this figure onto itself.
Question 20.

Answer:
A rectangle has two equal sides and all equal angles.
We have to determine which angles of rotation map the figure onto itself.
The interior angles are 90°
The angle of rotational symmetry for the rectangle is 180°
REPEATED REASONING
In Exercises 21-24, select the angles of rotational symmetry for the regular polygon. Select all that apply.
(A) 30° (B) 45° (C) 60° (D) 72°
(E) 90° (F) 120° (G) 144° (H) 180°
Question 21.
Answer: Option F
The angle of rotational symmetry of this figure is 120°
Question 22.

Answer:
The above figure has equal lengths of sides and angles.
The angles of rotational symmetry for the regular polygon are 90° and 180°.
Question 23.
Answer:
The above figure has equal lengths of sides and angles.
The angles of rotational symmetry for the regular polygon are 72° and 144°.
Question 24.
Answer:
The above figure has equal lengths of sides and angles.
The interior angles in the hexagon are 60°
The angles of rotational symmetry for the regular polygon are 60°, 120° and 180°
ERROR ANALYSIS
In Exercises 25 and 26, the endpoints of \(\overline{C D}\) are C(- 1, 1) and D(2, 3). Describe and correct the error in finding the coordinates of the vertices of the image after a rotation of 270° about the origin.
Question 25.
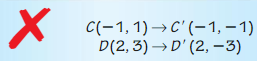
Answer:
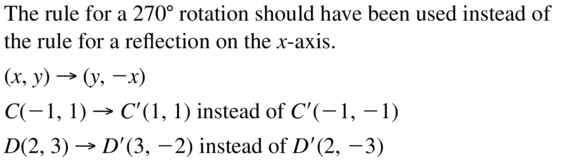
Question 26.
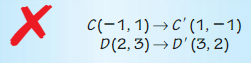
Answer:
Rotating 270° (a, b) → (b, -a)
Reflection about y = x
The correct answer is
C(-1, 1) = C'(1, 1)
D(2, 3) = D'(3, -2)
Question 27.
CONSTRUCTION
Follow these Steps to construct a rotation of ∆ABC by angle D around a point O. Use a compass and straightedge.
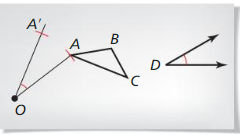
Step 1 Draw ∆ABC, ∠D, and O, the center of rotation.
Step 2 Draw \(\overline{O A}\). Use the construction for copying an angle to copy ∠D at O. as shown. Then use distance OA and center O to find A’.
Step 3 Repeat Step 2 to find points B’ and C’. Draw ∆ A’B’C’.
Answer:

Question 28.
REASONING
You enter the revolving door at a hotel.

a. You rotate the door 180°. what does this mean in the context of the situation? Explain.
Answer:
The revolving door is composed of 3 rectangular glass parts intersecting at the door axis.
In the context of our lesson, Rotating the revolving door 180° means rotating the short sides of the rectangles 180° about the origin.
b. You rotate the door 360°. What does this mean in the Context of the situation? Explain.
Answer:
Rotating the revolving door 360° means rotating the short sides of the rectangles 360° about the origin.
Question 29.
MATHEMATICAL CONNECTIONS
Use the graph of Y = 2X – 3.
a. Rotate the line 90°, 180° 270°, and 360° about the origin. Write the equation of the line for each image. Describe the relationship between the equation of the preimage and the equation of each image.
b. Do you think that the relationships you described in part (a) are true for any line? Explain your reasoning.
Answer:

Question 30.
MAKING AN ARGUMENT
Your friend claims that rotating a figure by 180° is the same as reflecting a figure in the y-axis arid then reflecting it in the x-axis. Is your friend correct? Explain your reasoning.
Answer:
rotating a figure by 180° (a, b) → (-a, -b)
reflecting a figure in the y-axis (a, b) → (-a, b)
reflecting a figure in the x-axis (a, b) → (a, -b)
For reflecting a figure in the y-axis and then reflecting in the x-axis
the first step will result (a, b) → (a, -b)
Reflecting (-a, b) in the x-axis (-a, b) → (-a, -b)
Thus your friend is correct.
Question 31.
DRAWING CONCLUSIONS
A figure only has point symmetry. How many times can you rotate the figure before it is back where it started?
Answer:
If a figure only has point symmetry, then it has 180° rotational symmetry. One rotation will rotate the figure 180°. A second rotation will rotate the figure another 180°. The two rotations combined result in a 360° rotation and therefore the rotations map the figure onto itself. So, you can rotate the figure 2 times before it is back where it started.
Question 32.
ANALYZING RELATIONSHIPS
Is it possible for a figure to have 90° rotational symmetry but not 180° rotational symmetry? Explain your reasoning.
Answer:
No, it is not possible.
When figure has 90° rotational symmetry, it must has 180° rotational symmetry.
When we rotate the figure twice by 90°, we get 180°
Question 33.
ANALYZING RELATIONSHIPS
Is it possible for a figure to have 180° rotational symmetry hut not 90° rotational symmetry? Explain your reasoning.
Answer:
Question 34.
THOUGHT PROVOKING
Can rotations of 90°, 180°, 270°, and 360° be written as the composition of two reflections? Justify your answer.
Answer:
1. 180°
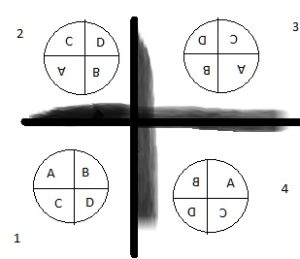
The 1st image is original. The vertical lines in the above image are mirrors.
So, if I use two reflections I get image 3 eventually from two possible paths.
Image 3 is the 180° rotation of original object 1.
2. 360° rotation
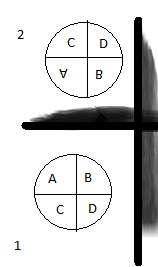
The 1st image is original. The horizontal lines in the above image are mirrors.
So, if I use two reflections – First take the reflection of 1st image to get it flipped.
Then again take reflection of this flipped image again to get original image.
Question 35.
USING AN EQUATION
Inside a kaleidoscope. two mirrors are placed next to each other to form a V. The angle between the mirrors determines the number of lines of symmetry in the image. Use the formula n(m∠1) = 180° to find the measure of ∠1, the angle between the mirrors, for the number n of lines of symmetry.
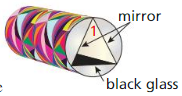
a.

b.

Answer:
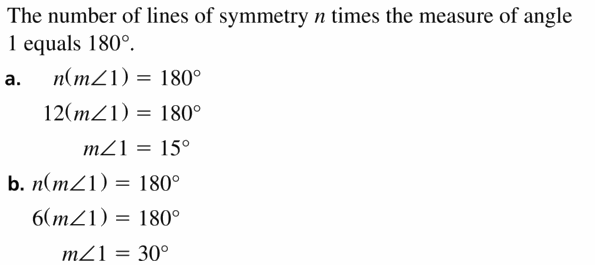
Question 36.
REASONING
Use the coordinate rules for counterclockwise rotations about the origin to write coordinate rules 11w clockwise rotations of 9o°. 180°, or 270° about the origin.
Answer:
For a rotation of 90° (a, b) = (b, -a)
For a rotation of 180° (a, b) = (-a, -b)
For a rotation of 270° (a, b) = (-b, a)
Question 37.
USING STRUCTURE
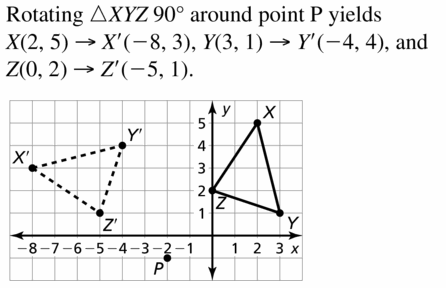
∆XYZ has vertices X(2, 5). Y(3, 1), and Z(0, 2). Rotate ∆XYZ 90° about the point P(- 2, – 1).
Answer:
Question 38.
HOW DO YOU SEE IT?
You are finishing the puzzle. The remaining two pieces both have rotational symmetry.

a. Describe the rotational symmetry of Piece 1 and of Piece 2.
Answer: The rotational symmetry of the two pieces are 180°
b. You pick up Piece 1. How many different ways can it fit in the puzzle?
Answer:
There are 2 different ways piece 1 can fit in the puzzle.
If we fit it in one of the two ways, we rotate it 180° to get the second way.
c. Before putting Piece 1 into the puzzle, you connect it to Piece 2. Now how many ways can it fit in the puzzle? Explain.
Answer:
If we connect piece 1 to piece 2 before putting them in the puzzle, there is only one way we can fit it in the puzzle.
Question 39.
USING STRUCTURE
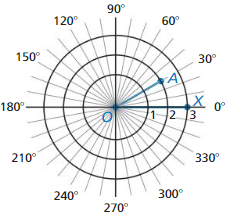
A polar coordinate system locates a point in a plane by its distance from the origin O and by the measure of an angle with its vertex at the origin. For example, the point A(2, 30°) is 2 units from the origin and m∠XOA = 30°. What are the polar coordinates of the image of point A after a 90° rotation? a 180° rotation? a 270° rotation? Explain.
Answer:

Maintaining Mathematical Proficiency
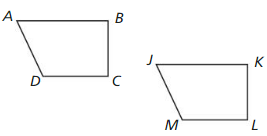
The figures are congruent. Name the corresponding angles and the corresponding sides.
Question 40.
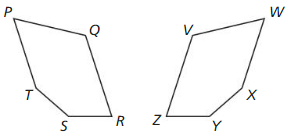
Answer:
Each of the figures is a reflection to the other on a vertical line between them
\(\overline{V W}\) ≅ \(\overline{Q P}\) and ∠V ≅ ∠Q
\(\overline{W X}\) ≅ \(\overline{P T}\) and ∠W ≅ ∠P
\(\overline{X Y}\) ≅ \(\overline{T S}\) and ∠X ≅ ∠T
\(\overline{Y Z}\) ≅ \(\overline{R S}\) and ∠Y ≅ ∠S
\(\overline{Z V}\) ≅ \(\overline{R Q}\) and ∠Z ≅ ∠R
Thus QPTSR ≅ VWXYZ
Question 41.
Answer:
4.1 – 4.3 Quiz
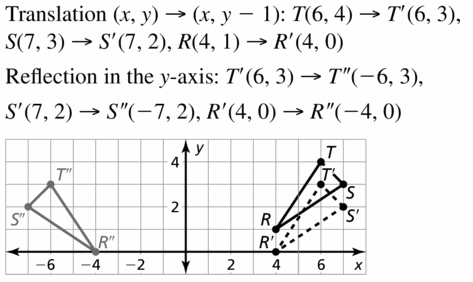
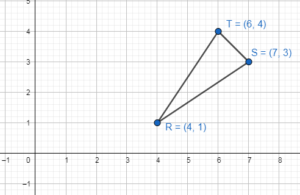
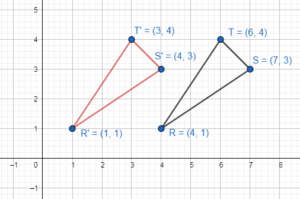
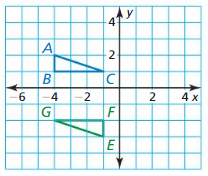
Graph quadrilateral ABCD with vertices A(- 4, 1), B(- 3, 3), C(0, 1), and D(- 2, 0) and its
image alter the translation.
Question 1.
(x, y) → (x + 4, y – 2)
Answer:
Given the vertices of the quadrilateral are A(- 4, 1), B(- 3, 3), C(0, 1), and D(- 2, 0)
translation: (x, y) → (x + 4, y – 2)
A(- 4, 1) → (-4 + 4, 1 – 2) → A'(0, -1)
B(- 3, 3) → (-3 + 4, 3 – 2) → B'(1, 1)
C(0, 1) → (0 + 4, 1 – 2) → C'(4, -1)
D(- 2, 0) → (-2 + 4, 0 – 2) → D'(2, -2)
Question 2.
(x, y) → (x – 1, y – 5)
Answer:
Given the vertices of the quadrilateral are A(- 4, 1), B(- 3, 3), C(0, 1), and D(- 2, 0)
Translation: (x, y) → (x – 1, y – 5)
A(- 4, 1) → (-4 – 1, 1 – 5) → A'(-5, -4)
B(- 3, 3) → (-3 – 1, 3 – 5) → B'(-4, -2)
C(0, 1) → (0 – 1, 1 – 5) → C'(-1, -4)
D(- 2, 0) → (-2 – 1, 0 – 5) → D'(-3, -5)
Question 3.
(x, y) → (x + 3, y + 6)
Answer:
Given the vertices of the quadrilateral are A(- 4, 1), B(- 3, 3), C(0, 1), and D(- 2, 0)
Translation: (x, y) → (x + 3, y + 6)
A(- 4, 1) → (-4 + 3, 1 + 6) = A’ (-1, 7)
B(- 3, 3) → (-3 + 3, 3 + 6) = B'(0, 9)
C(0, 1) → (0 + 3, 1 + 6) = C'(3, 7)
D(- 2, 0) → (-2 + 3, 0 + 6) = D'(1, 6)
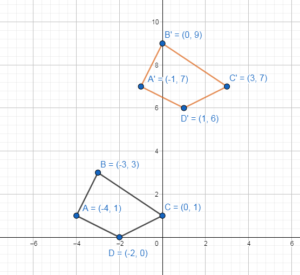
Graph the polygon with the given vertices and its image after a reflection in the given line.
Question 4.
A(- 5, 6), B(- 7, 8), c(- 3, 11); x – axis
Answer:
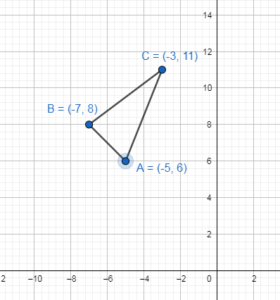
Now we will apply reflection in the x-axis to the ΔABC.
A(-5, 6) → A'(-5, -6)
B(-7, 8) → B'(-7, -8)
C(-3, 11) → C'(-3, -11)
The vertices are A'(-5, -6), B'(-7, -8) and C'(-3, -11)
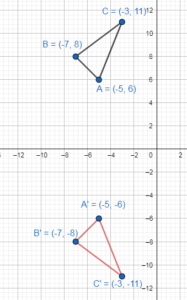
Question 5.
D(- 5, – 1), E(- 2, 1), F(- 1, – 3); y = x
Answer:
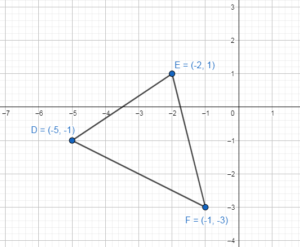
Apply reflection in the line y = x to the ΔDEF
D(- 5, – 1) → D'(-1, -5)
E(- 2, 1) → E'(1, -2)
F(- 1, – 3) → F'(-3, -1)
D'(-1, -5), E'(1, -2) and F'(-3, -1).
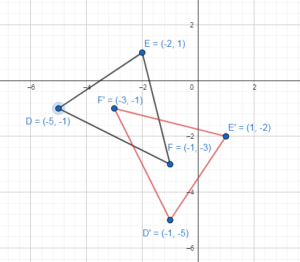
Question 6.
J(- 1, 4), K(2, 5), L(5, 2), M(4, – 1); x = 3
Answer:
J(- 1, 4), K(2, 5), L(5, 2), M(4, – 1); x = 3
J(- 1, 4) → J'(7, 4)
K(2, 5) → K'(4, 5)
L(5, 2) → L'(1, 2)
M(4, – 1) → M'(2, -1)
J'(7, 4), K'(4, 5), L'(1, 2) and M'(2, -1)
Question 7.
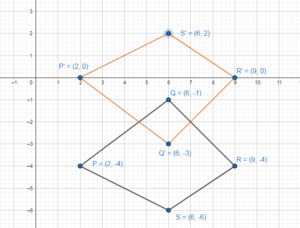
P(2, – 4), Q(6, – 1), R(9, – 4), S(6, – 6); y = – 2
Answer:
P(2, – 4), Q(6, – 1), R(9, – 4), S(6, – 6)
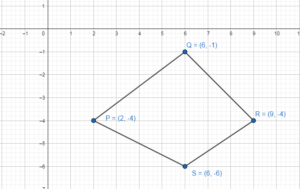
P(2, – 4) → P'(2, 0)
Q(6, – 1) → Q'(6, -3)
R(9, – 4) → R'(9, 0)
S(6, – 6) → S'(6, 2)
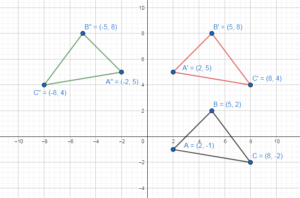
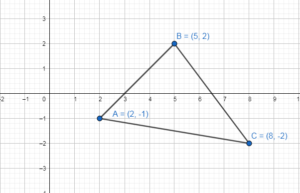
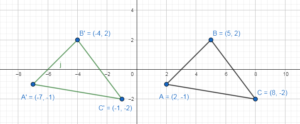
Graph ∆ABC with vertices A(2, – 1), B(5, 2), and C(8, – 2) and its image after the glide reflection.
Question 8.
Translation: (x, y) → (x, y + 6)
Reflection: in the y – axis
Answer:
A(2, – 1), B(5, 2), and C(8, – 2)
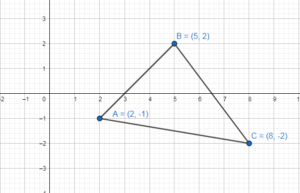
Translation: (x, y) → (x, y + 6)
A(2, -1) → (2, -1 + 6) = A'(2, 5)
B(5, 2) → (5, 2 + 6) = B'(5, 8)
C(8, – 2) → (8, -2 + 6) = C'(8, 4)
A'(2, 5), B'(5, 8) and C'(8, 4)
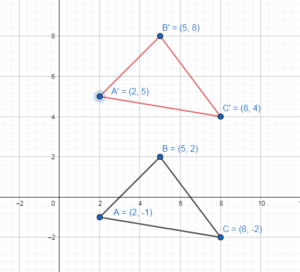
A'(2, 5) → A”(-2, 5)
B'(5, 8) → B”(-5, 8)
C'(8, 4) → C”(-8, 4)
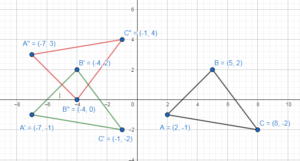
Question 9.
Translation: (x, y) → (x – 9, y)
Reflection: in the line y = 1
Answer:
A(2, – 1), B(5, 2), and C(8, – 2)
Translation: (x, y) → (x – 9, y)
A(2, – 1) → (2 – 9, -1) = A'(-7, -1)
B(5, 2) → (5 – 9, 2) = B'(-4, 2)
C(8, – 2) → (8 – 9, -2) = C'(-1, -2)
Apply reflection in the line y = 1 to the triangle A’B’C’
A'(-7, -1) → A”(-7, 3)
B'(-4, 2) → B”(-4, 0)
C'(-1, -2) → C”(-1, 4)
Determine the number of lines of symmetry for the figure.
Question 10.

Answer: The hexagon has 6 lines of symmetry.
Question 11.
Answer: The figure has no lines of symmetry. It cannot be reflected anyway.
Question 12.

Answer: The figure has two lines of symmetry.
Question 13.
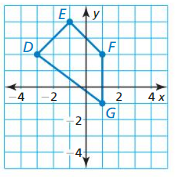
Answer: The figure has only 1 line of symmetry.
Graph the polygon and its image after a rotation of the given number of degrees about the origin.
Question 14.
90°
Answer: ABC with the vertices are A(1, 1), B(2, 4) and C(4, 1)
A(1, 1) through an angle 90° about the origin, A'(-1, 1)
B(2, 4) through an angle 90° about the origin, B'(-4, 2)
C(4, 1) through an angle 90° about the origin, C'(-1, 4)
Question 15.
270°
Answer:
Rotate D(-3, 2) through an angle 270° about the origin, we get D'(2, 3)
Rotate E(-1, 4) through an angle 270° about the origin, we get E'(4, 1)
Rotate F(1, 2) through an angle 270° about the origin, we get F'(2, -1)
Rotate G(1, -1) through an angle 270° about the origin, we get G'(-1, -1)
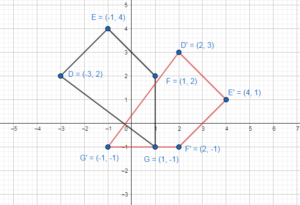
Question 16.
180°
Answer:
Rotating 180° (a, b) → (-a, -b)
H(-4, 1) → H'(4, -1)
I(-2, 2) → I'(2, -2)
J(-1, -2) → J'(1, 2)
K(-4, -4) → K'(4, 4)
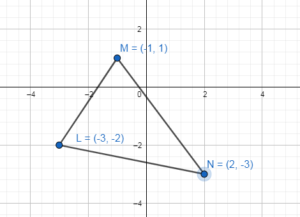
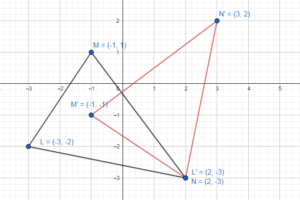
Graph ∆LMN with vertices L(- 3, – 2), M (- 1, 1), and N(2, – 3) and its image after
the composition.
Question 17.
Translation: (x, y) → (x – 4, y + 3)
Rotation: 180° about the origin
Answer:
L(- 3, – 2), M (- 1, 1), and N(2, – 3)
Translation: (x, y) → (x – 4, y + 3)
L(- 3, – 2) → (-3 – 4, -2 + 3) = L'(-7, 1)
M (- 1, 1) → (-1 – 4, 1 + 3) = M'(-5, 4)
N(2, – 3) → (2 – 4, -3 + 3) = N'(-2, 0)
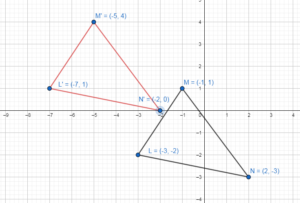
L'(-7, 1) through an angle 180° about the origin, we will get L”(7, -1).
M'(-5, 4) through an angle 180° about the origin, we will get M”(5, -4).
N'(-2, 0) through an angle 180° about the origin, we will get N”(2, 0).
L”(7, -1), M”(5, -4) and N”(2, 0)
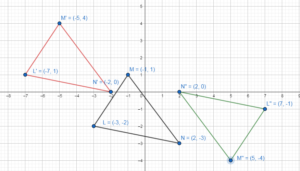
Question 18.
Rotation: 90° about the origin
Reflection: in the y-axis
Answer:
L(- 3, – 2), M (- 1, 1), and N(2, – 3)
L(- 3, – 2) through an angle 90° about the origin, we will get L'(2, -3)
M (- 1, 1) through an angle 90° about the origin, we will get M'(-1, -1)
N(2, – 3) through an angle 90° about the origin, we will get N'(3, 2)
L'(2, -3), M'(-1, -1) and N'(3, 2)
L” which is in the same place on opposite sides y-axis with respect to the point L'(2, -3)
L”(-2, -3)
M'(-1, -1) = M”(1, -1)
N'(3, 2) = N”(-3, 2)
L”(-2, -3), M”(1, -1), and N”(-3, 2) will be vertices of the triangle L”M”N”
Question 19.
The figure shows a game in which the object is to create solid rows using the pieces given. Using only translations and rotations, describe the transformations for each piece at the top that will form two solid rows at the bottom.
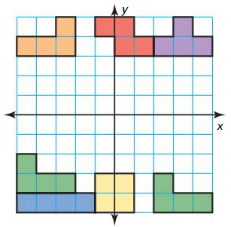
Answer:
Figure A can be moved on to its location A at the bottom of the chart by a rotation 90° anticlockwise followed by a translation of 4 units horizontally towards the right and 6 units downwards.
Figure B can be moved on to its location B at the bottom of the chart by translation of 3 units horizontally towards the right and 7 units downwards.
Figure C can be moved on to its location C at the bottom of the chart by a rotation 180° anticlockwise followed by a translation of 5 units horizontally towards the right and 7 units downwards.
4.4 Congruence and Transformations
Exploration 1
Reflections in Parallel Lines
Work with a partner. Use dynamic geometry software to draw any scalene triangle and label it ∆ABC.
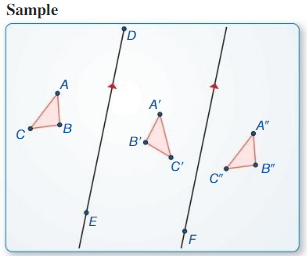
a. Draw an line ![]() . Reflect ∆ ABC in
. Reflect ∆ ABC in ![]() to form ∆A’B’C’.
to form ∆A’B’C’.
Answer:
b. Draw a line parallel to ![]() . Reflect ∆A’B’C’ in the new line to form ∆A”B”C”.
. Reflect ∆A’B’C’ in the new line to form ∆A”B”C”.
Answer:
c. Draw the line through point A that is perpendicular to ![]() . What do you notice?
. What do you notice?
Answer:
d. Find the distance between points A and A”. Find the distance between the two parallel lines. What do You notice?
Answer:
e. Hide ∆A’B’C’. Is there a single transformation that maps ∆ABC to ∆A”B”C”? Explain.
Answer:
f. Make conjectures based on your answers in parts (c)-(e). Test our conjectures by changing ∆ABC and the parallel lines.
CONSTRUCTING VIABLE ARGUMENTS
To be proficient in math, you need to make conjectures and justify your conclusions.
Answer:
Exploration 2
Reflections in Intersecting Lines
Work with a partner: Use dynamic geometry software to draw any scalene triangle and label it ∆ABC.
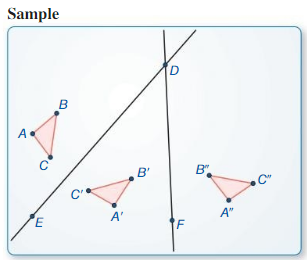
a. Draw an line ![]() . Reflect ∆ABC in
. Reflect ∆ABC in ![]() to form ∆A’B’C’.
to form ∆A’B’C’.
Answer:
b. Draw any line ![]() so that angle EDF is less than or equal to 90°. Reflect ∆A’B’C’ in
so that angle EDF is less than or equal to 90°. Reflect ∆A’B’C’ in ![]() to form ∆A”B”C”.
to form ∆A”B”C”.
Answer:
c. Find the measure of ∠EDF. Rotate ∆ABC counterclockwise about point D using an angle twice the measure of ∠EDF.
Answer:
d. Make a conjecture about a figure reflected in two intersecting lines. Test your conjecture by changing ∆ABC and the lines.
Answer:
Communicate your Answer
Question 3.
What conjectures can you make about a figure reflected in two lines?
Answer: The line of reflection is the perpendicular bisector of every segment joining a point in the original figure with its image.
Question 4.
Point Q is reflected in two parallel lines, ![]() and
and ![]() . to form Q’ and The distance from
. to form Q’ and The distance from ![]() to
to ![]() is 3.2 inches. What is the distance QQ”?
is 3.2 inches. What is the distance QQ”?
Answer:
Lesson 4.4 Congruence and Transformations
Monitoring Progress
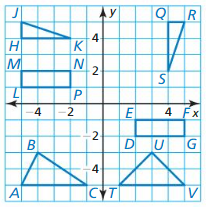
Question 1.
Identify any congruent figures in the coordinate plane. Explain.
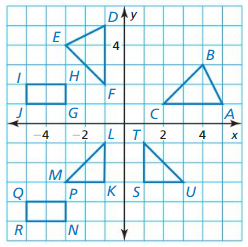
Answer:
A figure shown below is given, and it required to find congruent figure in coordinate plane, identify congruent figures in the coordinate plane by identifying the rigid motion or composition of rigid motions that maps one of the figures onto the other. using different transformation like translations, reflections, and rotations.
Rectangle NPQR is the translation of rectangle GHIJ 6 units down.
So, rectangle NPQR and GHIJ are congruent.
ΔKLM is a reflection of ΔSTU in the y-axis. So, ΔKLM and ΔSTU is congruent.
ΔDEF is 90° rotation of ΔABC about the origin.
So, ΔDEF and ΔABC are congruent.
Question 2.
In Example 2. describe another congruence transformation that maps ▱ABCD to ▱EFGH.
Answer:
Reflected over the x-axis and then translate 5 units left.
Question 3.
Describe a congruence transformation that maps △JKL to △MNP.
Answer:
J(-1, 2)
K(-3, 4)
L(-4, 2)
M(4, -2)
N(2, -4)
P(1, -2)
Reflect over the y-axis and translate 5 units right.
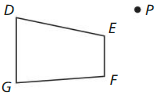
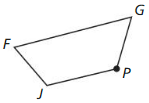
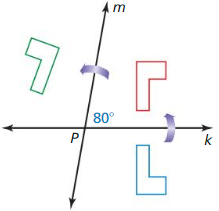
Use the figure. The distance between line k and line m is 1.6 centimeters.
Question 4.
The preimage is reflected in line k, then in line m. Describe a single transformation that maps the blue figure to the green figure.
Answer: Translation 3.2 cm to the right.
Question 5.
What is the relationship between \(\overline{P P’}\) and line k? Explain.
Answer: \(\overline{P P’}\) is perpendicular to line k by reflections in parallel lines.
Question 6.
What is the distance between P and P”?
Answer: 3.2 cm
Question 7.
In the diagram. the preimage is reflected in line k, then in line m. Describe a single transformation that maps the blue figure onto the green figure.
Answer: 160° rotation about point P.
Question 8.
A rotation of 76° maps C to C’. To map C to C’ Using two reflections, what is the measure of the angle formed by the intersecting lines of reflection?
Answer: 38°
Exercise 4.4 Congruence and Transformations
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
Two geometric figures are __________ if and only if there is a rigid motion or a composition of rigid motions that moves one of the figures onto the other.
Answer:
Two geometric figures are congruent if and only if there is a rigid motion or a composition of rigid motions that moves one of the figures onto the other.
Question 2.
VOCABULARY
Why is the term congruence transformation used to refer to a rigid motion?
Answer: preimage and image are congruent.
Monitoring Progress and Modeling with Mathematics
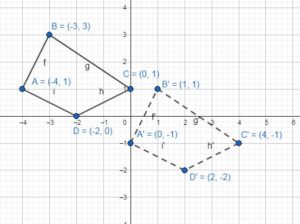
In Exercises 3 and 4, identify an congruent figures in the coordinate plane. Explain.
Question 3.
Answer:

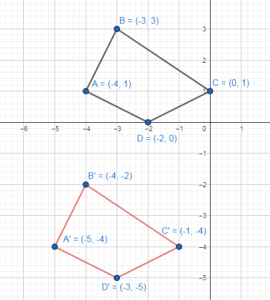
Question 4.
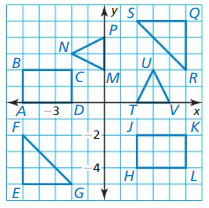
Answer:
Rectangle ABCD ≅ Rectangle HJKL
Both rectangle are 3 units length and 2 units width.
Rectangle HJKL is the image Rectangle ABCD after translating the second 7 units right and 4 units Down.
ΔMNP ≅ ΔTUV
Both triangles are isosceles with 2 units base and 2 units altitude.
ΔMNP is the image of ΔTUV after rotating the second 90°
Rotating 90° is (a, b) → (-b, a)
T(2, 0) → M(0, 2)
U(3, 2) → N(-2, 3)
V(4, 0) → P(0, 4)
ΔQRS ≅ ΔEFG
Both triangles are right isosceles with 3 units length.
ΔEFG is the image of ΔQRS after rotating the second 180°
Rotating 180° is (a, b) → (-a, -b)
Q(5, 5) → E(-5, -5)
R(5, 2) → F(-5, -2)
S(2, 5) → G(-2, -5)
In Exercises 5 and 6, describe a congruence transformation that maps the blue preimage to the green image.
Question 5.
Answer:
Question 6.
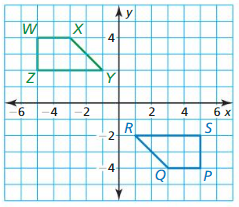
Answer:
The congruent transformation is 180° rotation about the origin.
180° rotation: (a, b) → (-a, -b)
P(5, -4) → W(-5, 4)
Q(3, -4) → X(-3, 4)
R(1, -2) → Y(-1, 2)
S(5, -2) → Z(-5, 2)
PQRS ≅ WXYZ
In Exercises 7-10. determine whether the polygons with the given vertices are congruent. Use transformations to explain your reasoning.
Question 7.
Q(2, 4), R(5, 4), S(4, 1) and T(6, 4), U(9, 4), V(8, 1)
Answer:
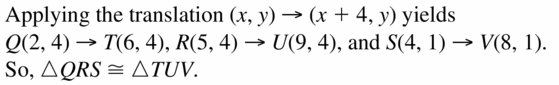
Question 8.
W(- 3, 1), X(2, 1), Y(4, -,4),,Z(- 5, – 4) and C(- 1, – 3) D(- 1, 2), E(4, 4), F(4, – 5)
Answer:
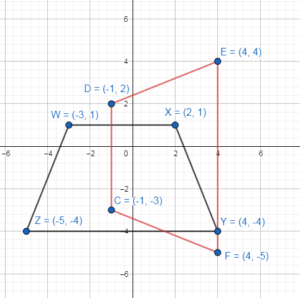
We have to check whether two polygons are congruent.
Now Rotate W(-3, 1) through an angle 90° about the origin, we will get C(-1, -3)
Now Rotate Y(4, -4) through an angle 90° about the origin, we will get E(4, 4)
Now Rotate X(2, 1) through an angle 90° about the origin, we will get D(-1, 2)
Now Rotate Z(-5, -4) through an angle 90° about the origin, we will get F(4, -5)
These two polygons are congruent when we apply rotation.
Question 9.
J(1, 1), K(3, 2), L(4, 1) and M(6, 1), N(5, 2), P(2, 1)
Answer:

Question 10.
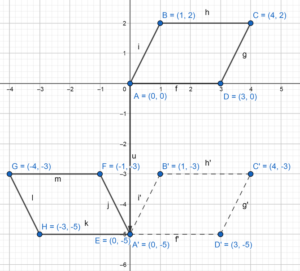
A(0, 0), B(1, 2), C(4, 2), D(3, 0) and E(0, – 5), F( – 1, – 3), G(- 4, – 3), H(- 3, – 5)
Answer:
A(0, 0), B(1, 2), C(4, 2), D(3, 0)
(x, y) → (x, y – 5)
A(0, 0) → A'(0, -5)
B(1, 2) → B'(1, -3)
C(4, 2) → C'(4, -3)
D(3, 0) → D'(3, -5)
Then reflecting the image A’B’C’D’ in the y-axis with the rule
(x, y) → (-x, y)
A'(0, -5) → A”(0, -5) ≅ E
B'(1, -3) → B”(-1, -3) ≅ F
C'(4, -3) → C”(-4, -3) ≅ G
D'(3, -5) → D”(-3, -5) ≅ H
So, ABCD ≅ EFGH
In Exercises 11-14, k || m, ∆ABC is reflected in line k, and ∆A’B’C” is reflected in line in.
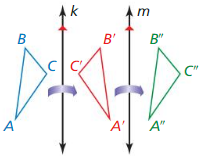
Question 11.
A translation maps ∆ABC onto which triangle?
Answer:
![]()
Question 12.
Which lines are perpendicular to \(\overline{A A”}\)?
Answer: The lines k and m are perpendicular
Question 13.
If the distance between k and m is 2.6 inches. what is the length of \(\overline{C C”}\)?
Answer:
![]()
Question 14.
Is the distance from B’ to in the same as the distance from B” to m? Explain.
Answer:
The lines k and m are parallel.
The triangle ABC is reflected in the line k.
The triangle ABC is reflected in the line m.
Let us apply reflection in the line m to the triangle A’B’C’
Point A’ which is in the same place on opposite sides from the line m with respect to the point A”
Point B’ which is in the same place on opposite sides from the line m with respect to the point B”
Point C’ which is in the same place on opposite sides from the line m with respect to the point C”
When we join point B and point B”, then we get \(\overline{B B”}\)”
The distance from B’ to m is the same as the distance from B” to m.
In Exercises 15 and 16, find the angle of rotation that maps A onto A”.
Question 15.
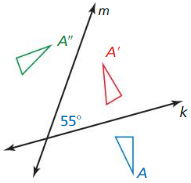
Answer:
![]()
Question 16.
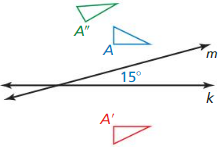
Answer:
In the intersection of the line m and the line n there is a point that we will mark with M.
When we join point A and point M, then we get \(\overline{A M}\)
When we join point A” and point M, then we get \(\overline{A” M}\)
Now observe at the angle ∠AMA’
∠AMA” = 2 × 15 = 30
Question 17.
ERROR ANALYSIS
Describe and correct the error in describing the congruence transformation.
Answer:
Question 18.
ERROR ANALYSIS
Describe and correct the error in using the Reflections in Intersecting Lines Theorem
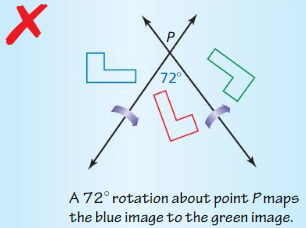
Answer:
When a figure is reflected in two intersecting lines, then the image is a rotation of the preimage about the point of intersection of the 2 reflecting lines through an angle between the intersecting lines.
This means that the blue figure should be rotated about the point of intersection by
72° × 2 = 144° anticlockwise to obtain the image of given preimage.
The solution shown here is incorrect because the reflection is done in the first line first, followed by the reflection in the second line, which is incorrect.
In Exercises 19 – 22, find the measure of the acute or right angle formed by intersecting lines so that C can be mapped to C’ using two reflections.
Question 19.
A rotation of 84° maps C to C’.
Answer:

Question 20.
A rotation of 24° maps C to C’.
Answer:
By using the theorem we can find the measure of the angle formed by two intersecting lines.
In the intersection of the line m and the line n there is a point that we will mark with M.
When we join point C and point M, then we get \(\overline{C M}\)
When we join point C’ and point M, then we get \(\overline{C’ M}\)
Now observe at the angle ∠CMC’
∠CMC’ = 24
84/2 = 12
Question 21.
The rotation (x, y) → (- x, – y) maps C to C’.
Answer:

Question 22.
The rotation (x, y) → (y, – x) maps C to C’.
Answer:
The rotation (x, y) → (y, – x) is a 270° counterclockwise rotation, that is equivalent to 90° clockwise rotation.
The reflection on intersecting lines theorem considers the acute or right angle of the intersecting lines.
So, we will consider that the rotation is 90° clockwise
The angle of intersection is 45°
Question 23.
REASONING
Use the Reflection in Parallel Lines Theorem (Theorem 4.2) to explain how you can make a glide reflection using three reflections. How are the lines of reflection related?
Answer:

Question 24.
DRAWING CONCLUSIONS
The pattern shown is called a tessellation.

a. What transformations did the artist use when creating this tessellation?
Answer: The artist used translation and rotation in creating the tessellation.
b. Are the individual figures in the tessellation congruent? Explain your reasoning.
Answer: The individual figures are congruent to connect each other.
CRITICAL THINKING
In Exercises 25-28, tell whether the statement is away, sometime or never true. Explain your reasoning.
Question 25.
A Congruence transformation changes the size of a figure.
Answer: Never; A congruence transformation is a rigid motion that preserves length and angle measurement.
Question 26.
If two figures are Congruent, then there is a rigid motion or a composition of rigid motions that maps one figure onto the other.
Answer:
This statement is always true, because if two figures are congruent.
Then there is a grid motion or a composition of rigid motions that maps one figure onto the other.
Question 27.
The composition of two reflections results in the same image as a rotation.
Answer:
Sometimes; Reflecting in y =x and then y = x is not a rotation. Reflecting in the y-axis and then the x-axis is a rotation of 180°
Question 28.
A translation results in the same image as the composition of two reflections.
Answer: The statement is sometimes true because depends on the position.
Question 29.
REASONING
During a presentation, a marketing representative uses a projector so everyone in the auditorium can view the advertisement. Is this projection a congruence transformation? Explain your reasoning.
Answer:
No; the preimage is smaller than the projected image.
Question 30.
HOW DO YOU SEE IT?
What type of congruence transformation can be used to verify each statement about the stained glass window?
a. Triangle 5 is congruent to Triangle 8.
Answer: Triangle 5 can be mapped on to triangle 8 by a translation towards right.
b. Triangle 1 is congruent to Triangle 4.
Answer: Triangle 1 and Triangle 4 are congruent as they are reflection of one another in the line perpendicular to their common smaller acute angle vertex.
c. Triangle 2 is congruent to Triangle 7.
Answer: Triangle 2 can be mapped on to triangle 7 by 90° clockwise rotation.
d. Pen1aon 3 is congruent to Pentagon 6.
Answer: Pentagon 3 can be mapped on to pentagon 6 by a reflection in the horizontal followed by a rotation.
Question 31.
PROVING A THEOREM
Prove the Reflections in Parallel Lines Theorem (Theorem 4.2).
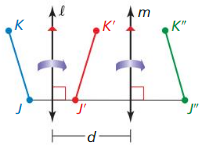
Given A reflection in line l maps \(\overline{J K}\) to \(\overline{J’ K’}\).
a reflection in line in maps \(\overline{J’ K’}\) to \(\overline{J” K”}\).
and l || m.
Prove a. \(\overline{K K”}\) is perpendicular to l and m. b. KK” = 2d, where d is the distance between l and m.
Answer:


Question 32.
THOUGHT PROVOKING
A tessellation is the covering of a plane with congruent figures so that there are no gaps or overlaps (see Exercise 24). Draw a tessellation that involves two or more types of transformations. Describe the transformations that are used to create the tessellation.
Answer:

A tessellation using equuilateral triangles transformation types used are
180° rotation to construct opposite triangles.
Translation to construct adjacent triangles.
Question 33.
MAKING AN ARGUMENT
\(\overline{P Q}\), with endpoints P(1, 3) and Q(3, 2). is reflected in the y-axis. The image \(\overline{P’ Q’}\) is then reflected in the x-axis to produce the image \(\overline{P” Q”}\). One classmate says that \(\overline{P Q}\) is mapped to \(\overline{P” Q”}\) by the translation (x, y) → (x – 4, y – 5). Another classmate says that \(\overline{P Q}\) is mapped to \(\overline{P” Q”}\) by a (2 • 90)°, or 180°, rotation about the origin. Which classmate is correct? Explain your reasoning.
Answer:

Question 34.
CRITICAL THINKING
Does the order of reflections for a composition of two reflections in parallel lines matter? For example, is reflecting ∆XYZ in line l and then its image in line in the same as reflecting ∆XYZ in line in and then its image in line l ?
Answer:
Yes, the order of reflections for a composition of two reflections in parallel lines matter.
When reflecting ΔXYZ the places of the middle images ΔX’Y’Z’ and the final images ΔX”Y”Z” will differ between the two cases.
In this case the reflecting ΔXYZ in l then m, results middle image ΔX’Y’Z’ between l and m. and the final image ΔX”Y”Z” after the line m.
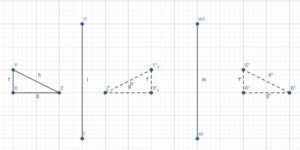
In this case the reflecting ΔXYZ in l then m, results middle image ΔX’Y’Z’ to the extreme right of the two lines l and m and the final image ΔX”Y”Z” to the extreme left to the two lines l and m.

CONSTRUCTION
In Exercises 35 and 36. copy the figure. Then use a compass and straightedge to construct two lines of reflection that produce a composition of reflections resulting in the same image as the given transformation.
Question 35.
Translation: ∆ABC → ∆A”B”C”

Answer:
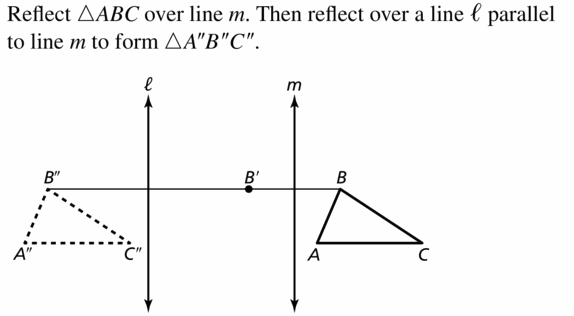
Question 36.
Rotation about P: ∆XYZ → ∆X”Y”Z”
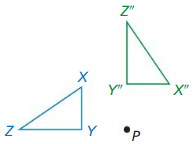
Answer:
Two construct the two reflections lines that produce ∆XYZ → ∆X”Y”Z equivalent to rotation about P.
Connecting \(\overline{P Y}\) and \(\overline{P Y”}\) and bisecting ∠YPY”
The bisector of ∠YPY” is the first line of reflection and \(\overline{P Y”}\) is the second one.
Maintaining Mathematical Proficiency
Solve the equation. Check your solution.
Question 37.
5x + 16 = – 3x
Answer:
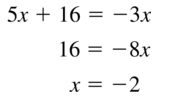
Question 38.
12 + 6m = 2m
Answer:
6m – 2m = 12
4m = 12
m = 12/4
m = 3
Question 39.
4b + 8 = 6b – 4
Answer:
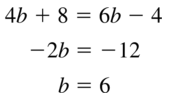
Question 40.
7w – 9 = 13 – 4w
Answer:
7w + 4w = 13 + 9
11w = 22
w = 22/11
w = 2
Question 41.
7(2n + 11) = 4n
Answer:
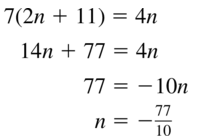
Question 42.
-2(8 – y) = – 6y
Answer:
-2(8 – y) = – 6y
-16 + 2y = -6y
-16 = -6y – 2y
-16 = -8y
y = 2
Question 43.
Last year. the track team’s yard sale earned $500. This year. the yard sale earned $625. What is the percent of increase?
Answer:
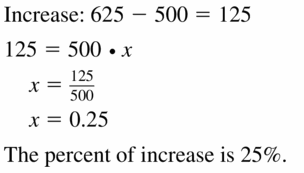
4.5 Dilations
Exploration 1
Dilating a Triangle in a Coordinate Plane
Work with a partner: Use dynamic geometry software to draw any triangle and label
it ∆ABC.
a. Dilate ∆ABC using a scale factor of 2 and a center of dilation at the origin to form ∆A’B’C’. Compare the coordinates, side lengths. and angle measures of ∆ABC and ∆A’B’C’.
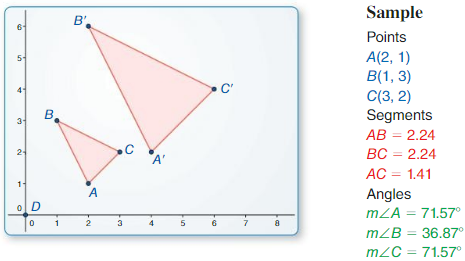
Answer:
b. Repeat part (a) using a scale factor of \(\frac{1}{2}\)
LOOKING FOR STRUCTURE
To be proficient in math, you need to look closely to discern a pattern or structure.
Answer:
c. What do the results of parts (a) and (b) suggest about the coordinates, side lengths, and angle measures of the image of ∆ABC after a dilation with a scale factor of k?
Answer:
Exploration 2
Dilating Lines in a Coordinate Plane
Work with a partner. Use dynamic geometry software to draw ![]() that passes through the origin and
that passes through the origin and ![]() that does not pass through the origin.
that does not pass through the origin.
a. Dilate ![]() using a scale factor of 3 and a center of dilation at the origin. Describe the image.
using a scale factor of 3 and a center of dilation at the origin. Describe the image.
Answer:
b. Dilate ![]() using a scale factor of 3 and a center of dilation at the origin. Describe the image.
using a scale factor of 3 and a center of dilation at the origin. Describe the image.
Answer:
c. Repeat parts (a) and (b) using a scale factor of \(\frac{1}{4}\)
Answer:
d. What do you notice about dilations of lines passing through the center of dilation and dilations of lines not passing through the center of dilation?
Answer:
Communicate Your Answer
Question 3.
What does it mean to dilate a figure?
Answer:
Dilatation of a figure means to enlarge and reduce the figure with a fixed point and a scale factor.
Question 4.
Repeat Exploration 1 using a center of dilation at a point other than the origin.
Answer:
Given vertices of a triangle ABC
A(2, 1), B(1, 3) and C(3, 2)
k = 2 and O(1, 2)
OA’ = 2OA
OB’ = 2OB
OC’ = 2OC
which is A'(3, 0), B'(1, 4) and C'(5, 2)
Lesson 4.5 Dilations
Monitoring Progress
Question 1.
In a dilation. CP’ = 3 and CP = 12. Find the scale factor. Then tell whether the dilation is a reduction or an enlargement.
Answer:
Given,
In a dilation. CP’ = 3 and CP = 12.
3/12 = 1/4
k = 1/4
The dilation is a reduction.
Graph ∆PQR and its image alter a dilation with scale factor k.
Question 2.
P(- 2, – 1), Q(- 1, 0), R(0, – L); k = 4
Answer:
Use the coordinate rule for a dilation with k = 4 to find the coordinates of the vertices of the image.
(x, y) → (4x, 4y)
P(-2, -1) → P'(4(-2), 4(-1)) = P'(-8, -4)
Q(-1, 0) → Q'(-1(4), 0(4)) = Q'(-4, 0)
R(0, – 1) → R'(4(0), 4(-1)) = R'(0, -4)
Question 3.
P(5, – 5), Q( 10, – 5), R( 10, 5); k = 0.4
Answer:
Question 4.
Graph ∆PQR with vertices P(1, 2), Q(3, 1). and R( 1, – 3) and its image after a dilation with a scale factor of – 2.
Answer:
P'(-2, -4)
Q'(-6, -2)
R'(-2, 6)
Question 5.
Suppose a figure containing the origin is dilated. Explain why the corresponding point in the image of the figure is also the origin
Answer:
According to the coordinate rule for dilations. if the origin P(0, 0) is the preimage of a point, then its image after a dilation centered at the origin with a scale factor k is the point P'(k0, k0) which is also the origin.
Question 6.
An optometrist dilates the pupils of a patient’s eyes to get a better look at the back of the eyes. A pupil dilates from 4.5 millimeters to 8 millimeters. What is the scale factor of this dilation?
Answer:
Given,
An optometrist dilates the pupils of a patient’s eyes to get a better look at the back of the eyes.
A pupil dilates from 4.5 millimeters to 8 millimeters.
= 8/4.5 = 80/45 = k
Question 7.
The image of a spider seen through the magnifying glass in Example 6 is shown at the left. Find the actual length of the spider.

Answer:
Given,
The image of spider = 12.6 cm
The factor = 6
Let x be the length of the spider and x’ be the length of the spider after magnification.
Let K be the factor of dilation or magnification.
K = x’/x
K = 6
x’ = 12.6
6 = 12.6/x
6x = 12.6
6x/6 = 12.6/6
x = 2.1
The length of the spider is 2.1 centimeters.
Exercise 4.5 Dilations
Vocabulary and Core Concept Check
Question 1.
COMPLETE THE SENTENCE
If P(x. y) is the preimage of a point, then its image after a dilation centered at the origin (0, 0) with scale factor k is the point _________.
Answer:
If P(x. y) is the preimage of a point, then its image after a dilation centered at the origin (0, 0) with scale factor k is the point P'(kx, ky).
Question 2.
WHICH ONE DOESNT BELONG?
Which scale factor does not belong with the other three? Explain your reasoning.
\(\frac{5}{4}\) 60% 115% 2
Answer:
2 scale factor does not belong with the other 3. Because it is an integer while the others are fractions.
Monitoring Progress Modeling with Mathematics
In Exercises 3-6. find the scale factor of the dilation. Then tell whether the dilation is a reduction or an enlargement.
Question 3.
Answer:
![]()
Question 4.
Answer:
To find the scale factor put P’/P
24/9 = 8/3, which is enlargement.
Question 5.
Answer:
To find the scale factor put P’/P
9/15 = 3/5, which is a reduction.
Question 6.
Answer:
To find the scale factor put P’/P
28/8 = 7/2
If P’ is greater than P than it is an enlargement.
CONSTRUCTION
In Exercises 7-10. copy the diagram. Then use a compass and straightedge to construct a dilation of ∆LMN with the given center and scale factor k.
Question 7.
Center C, k = 2
Answer:
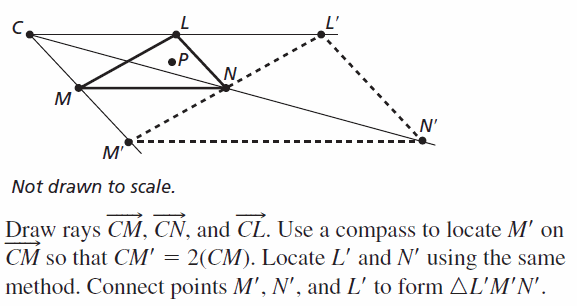
Question 8.
Center P, k = 3
Answer:
Question 9.
Center M, k = \(\frac{1}{2}\)
Answer:
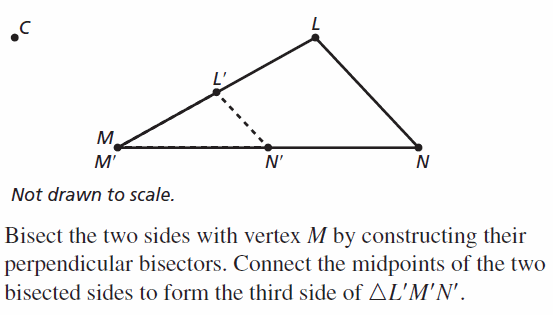
Question 10.
Center C. k = 25%
Answer:
CONSTRUCTION
In Exercises 11-14, copy the diagram. Then use a coin pass and straightedge to construct a dilation of quadrilateral RSTU with the given center and scale factor k.
Question 11.
Center C, k = 3
Answer:
Question 12.
Center P, k = \(\frac{1}{3}\)
Answer:
Question 13.
Center P, k = 0.25
Answer:
Question 14.
Center C, k = 75%
Answer:
In Exercises 15-18, graph the polygon and its image after a dilation with scale factor k.
Question 15.
X(6, – 1), Y(- 2, – 4), Z(1, 2); k = 3
Answer:
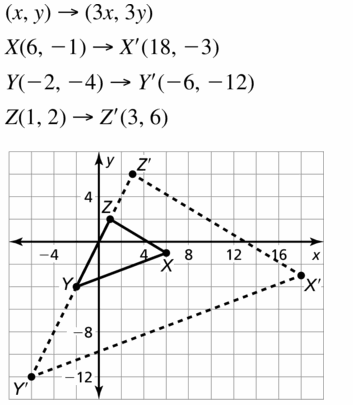
Question 16.
A(0, 5), B(- 10, – 5), C(5, – 5); k = 12o%
Answer:
Question 17.
T(9, – 3), U(6, 0), V(3, 9), W(0. 0); k = \(\frac{2}{3}\)
Answer:
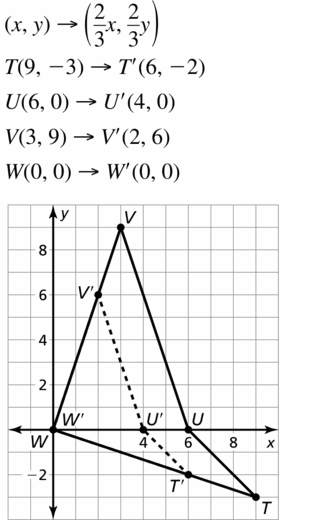
Question 18.
J(4, 0), K(- 8, 4), L(0, – 4), M(12, – 8);k = 0. 25
Answer:
J(4, 0) → J'(4 × 1/4, 0 × 1/4) = (1, 0)
K(-8, 4) → K'(-8 × 1/4, 4 × 1/4) = (-2, 1)
L(0, -4) → L'(0 × 1/4, -4 × 1/4) = (0, -1)
M(12, -8) → M'(12 × 1/4, -8 × 1/4) = (3, -2)
In Exercises 19-22, graph the polygon and its image after a dilation with scale factor k.
Question 19.
B(- 5, – 10), C(- 10, 15), D(0, 5); k = 3
Answer:
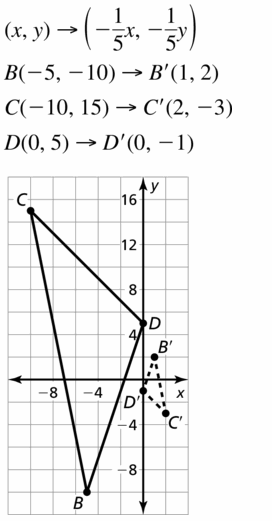
Question 20.
L(0, 0), M(- 4, 1), N(- 3, – 6); k = – 3
Answer:
Question 21.
R(- 7, – 1), S(2, 5), T(- 2, – 3), U(- 3,- 3); k = – 4
Answer:
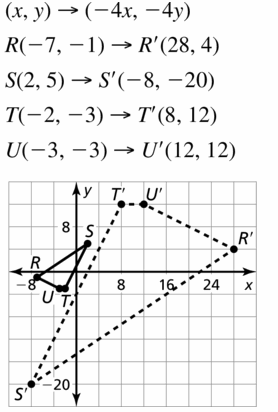
Question 22.
W(8, – 2), X(6, 0), Y(- 6, 4), Z(- 2, 2); k = – 0.5
Answer:
We need to use the coordinate rule for dilation with scale factor k = -0.5 to find the coordinates of the vertices.
(x, y) → (-0.5x, -0.5y)
W(8, -2) → W'(-0.5 × 8, -0.5 × (-2)) = W'(-4, 1)
X(6, 0) → X'(-0.5 × 6, -0.5 × 0) = X'(-3, 0)
Y(-6, 4) → Y'(-0.5 × (-6), -0.5 × 4) Y'(3, -2)
Z(-2, 2) → Z'(-0.5 × (-2). -0.5 × 2) = Z'(1, -1)
ERROR ANALYSIS
In Exercises 23 and 24, describe and correct the error in finding the scale factor of the dilation.
Question 23.
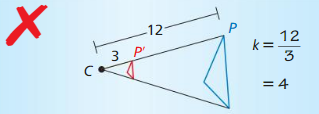
Answer:
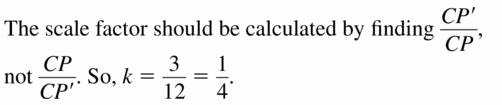
Question 24.
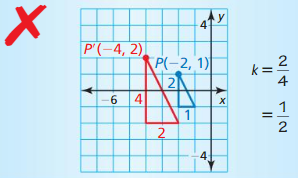
Answer:
A side length of the original triangle in blue is 2, and a side length of its image is 4.
The scale factor is a ratio of a side length of the image triangle to a side length of the original triangle.
scale factor k = 4/2 = 2
In Exercises 25-28, the red figure is the image of the blue figure after a dilation with center C. Find the scale factor of the dilation. Then find the value of the variable.
Question 25.
Answer:

Question 26.
Answer:
To find the scale factor put P’/P
28/14 = 2
12 × 1/2 = 6
Question 27.
Answer:

Question 28.
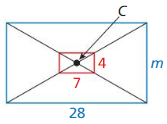
Answer:
The length of the original rectangle is 28
The length of its image after dilation with the center C and scale facator k is 7.
k = 7/28
k = 1/4
k = length of the image/length of the actual image
4/m = 1/4
1/m = 1/16
m = 16
Question 29.
FINDING A SCALE FACTOR
You receive wallet-sized photos of your school picture. The photo is 2.5 inches by 3.5 inches. You decide to dilate the photo to 5 inches by 7 inches at the store. What is the scale factor of this dilation?
Answer:
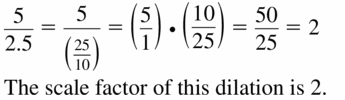
Question 30.
FINDING A SCALE FACTOR
Your visually impaired friend asked you to enlarge your notes from class so he can study. You took notes on 8.5-inch by 11-inch paper. The enlarged copy has a smaller side with a length of 10 inches. What is the scale factor of this dilation?
Answer:
The scale factor is a ratio of a side length of the copy image to a side length of the original notes.
k = 10/8.5
k = 100/85
k = 20/17
In Exercises 31-34, you are using a magnifying glass. Use the length of the insect and the magnification level to determine the length of the image seen through the magnifying glass.
Question 31.
emperor moth
Magnification: 5×

Answer:
The length of the image of the emperor moth is
5 × 60 = 300 millimeters
Question 32.
ladybug
Magnification: 10×

Answer:
image length = 4.5 mm × 10
= 45 mm
Thus the image length of ladybug is 45mm.
Question 33.
dragonfly
Magnification: 20×

Answer:
The length of the image of the dragonfly is
20 × 47 = 940 millimeters
Question 34.
carpenter ant
Magnification: 15×

Answer:
Carpenter ant length = 12mm
Magnification = 15x
The length of the image = 15 × 12 = 180 mm
Now convert from mm to cm
180 mm = 18 cm
Question 35.
ANALYZING RELATIONSHIPS
Use the given actual and magnified lengths to determine which of the following insects were looked at using the same magnifying in glass. Explain your reasoning.

Answer:

Question 36.
THOUGHT PROVOKING
Draw ∆ABC and ∆A’B’C’ so that ∆A’B’C’ is a dilation of ∆ABC. Find the center of dilation and explain how you found it.
Answer:
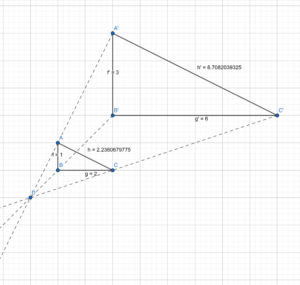
The point of concurrency of the 3 lines connecting each point to its image is the center of dilation.
Question 37.
REASONING
Your friend prints a 4-inch by 6-inch photo for you from the school dance. All you have is an 8-inch by 10-inch frame. Can you dilate the photo to fit the frame? Explain your reasoning.
Answer:
No, the scale factor for the shorter sides is 8/4 = 2, but the scale factor for the longer sides is 10/6 = 5/3.
The scale factor for both sides has to be the same or the picture will be disturbed.
Question 38.
HOW DO YOU SEE IT?
Point C is the center of dilation of the images. The scale factor is \(\frac{1}{3}\). Which figure is the original figure? Which figure is the dilated figure? Explain your reasoning.

Answer:
The larger star is the original figure while the smaller star is the dilated image.
Since 1/3 is less than one but more than 0, the image should be reduced thus making the smaller star the dilated figure.
Question 39.
MATHEMATICAL CONNECTIONS
The larger triangle is a dilation of the smaller triangle. Find the values of x and y.
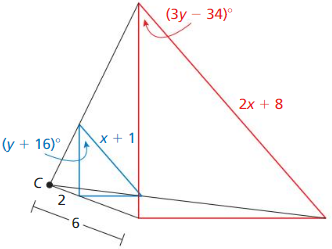
Answer:
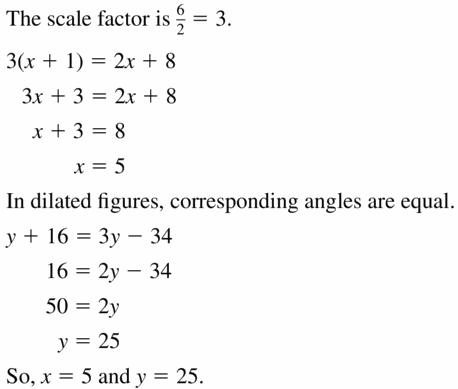
Question 40.
WRITING
Explain why a scale factor of 2 is the same as 200%.
Answer:
to convert a percentage into a whole number, divide by 100.
200% = 200/100 = 2
In Exercises 41-44, determine whether the dilated figure or the original figure is closer to the center of dilation. Use the given location of the center of dilation and scale factor k.
Question 41.
Center of dilation: inside the figure; k = 3
Answer:
With a scale factor of 3, this indicates that the dilated figure is larger than the original (3 > 1).
So, the original figure is closer to the center of dilation, which is inside both.
Question 42.
Center of dilation: inside the figure; k = \(\frac{1}{2}\)
Answer:
Since k < 1, Then the dilation is the reduction and the original image is closest to the center of dilation.
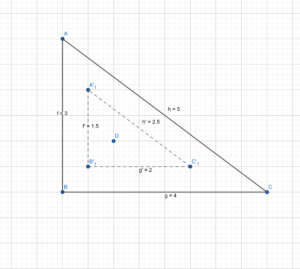
Question 43.
Center of dilation: outside the figure; k = 120%
Answer:
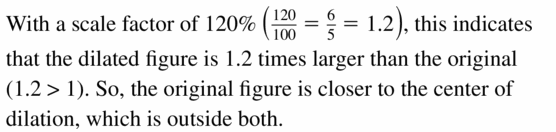
Question 44.
Center of dilation: outside the figure; k = 0. 1
Answer:
Since k < 1, Then the dilation is the enlargement and the original image is closest to the center of dilation.
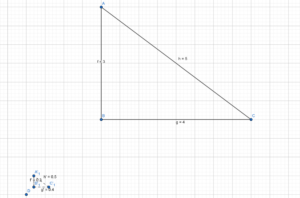
Question 45.
ANALYZING RELATIONSHIPS
Dilate the line through 0(0, 0) and A(1, 2) using a scale factor of 2.
a. What do you notice about the lengths of \(\overline{O’ A’}\) and \(\overline{O A}\)?
b. What do you notice about ![]()
Answer:
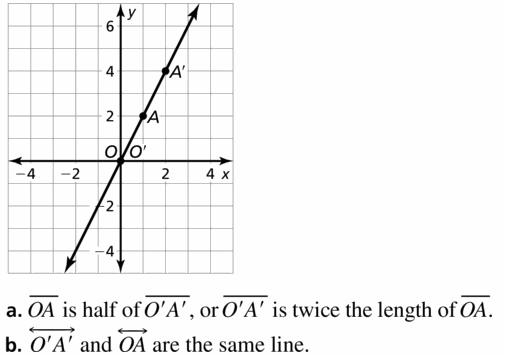
Question 46.
ANALYZING RELATIONSHIPS
Dilate the line through A(0, 1) and B( 1, 2) using a scale factor of \(\frac{1}{2}\).
a. What do you notice about the lengths of \(\overline{A’ B’}\) and \(\overline{A B}\)?
Answer:
It is clear that the length of \(\overline{O’ B’}\) is half the length of \(\overline{O B}\)
b. What do you notice about ![]() ?
?
Answer:
\(\overline{O’ B’}\) ia parallel to \(\overline{O B}\)
Question 47.
ATTENDING TO PRECISION
You are making a blueprint of your house. You measure the lengths of the walls of your room to be 11 feet by 12 feet. When you draw your room on the blueprint, the lengths of the walls are 8.25 inches by 9 inches. What scale factor dilates your room to the blueprint?
Answer:

Question 48.
MAKING AN ARGUMENT
Your friend claims that dilating a figure by 1 is the same as dilating a figure by – 1 because the original figure will not be enlarged or reduced. Is your friend correct? Explain your reasoning.
Answer:
Dilating a figure with scale factor 1 is not the same as a dilating a figure with scale factor -1.
Question 49.
USING STRUCTURE
Rectangle WXYZ has vertices W(- 3, – 1), X(- 3, 3), Y(5, 3), and Z(5, – 1).
a. Find the perimeter and area of the rectangle.
b. Dilate the rectangle using a scale factor of 3. Find the perimeter and area of the dilated rectangle. Compare with the original rectangle. What do you notice?
c. Repeat part (b) using a scale factor of \(\frac{1}{4}\).
d. Make a conjecture for how the perimeter and area change when a figure is dilated.
Answer:
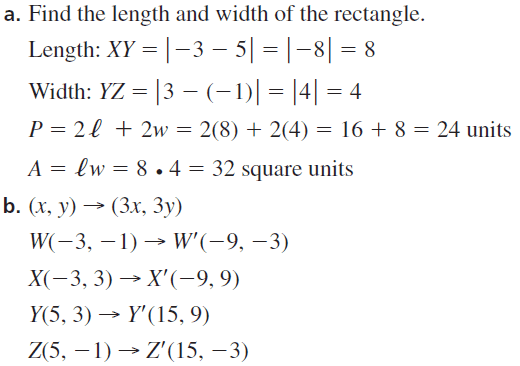

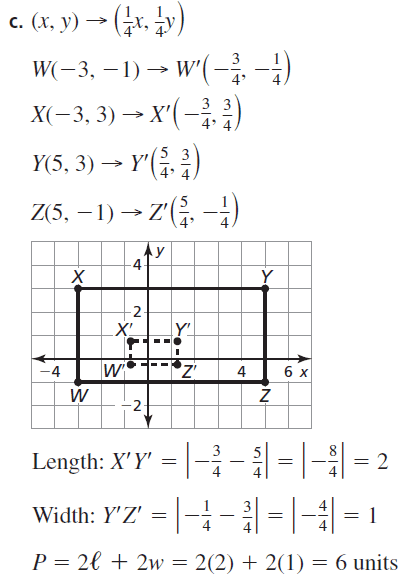

Question 50.
REASONING
You put a reduction of a page on the original page. Explain why there is a point that is in the same place on both pages.
Answer:
The center of dilation is the common point on both pages, so that must be present, that is on the same place on both pages.
Question 51.
REASONING
∆ABC has vertices A(4, 2), B(4, 6), and C(7, 2). Find the coordinates of the vertices of the image alter a dilation with center (4, 0) and a scale factor of 2.
Answer:
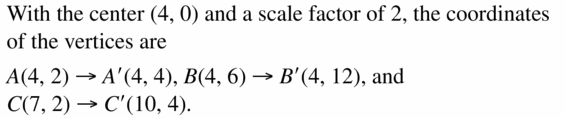
Maintaining Mathematical Proficiency
The vertices of ∆ABC are A(2,- 1), B(0, 4), and C(- 3, 5). Find the coordinates of the vertices of the image after the translation.
Question 52.
(x, y) → (x, y – 4)
Answer:
translation (x, y) → (x, y – 4)
The vertices of ∆ABC are A(2,- 1), B(0, 4), and C(- 3, 5)
A(2,- 1) → A'(2, -5)
B(0, 4) → B'(0, 0)
C(-3, 5) → C'(-3, 1)
Question 53.
(x, y) → (x – 1, y + 3)
Answer:
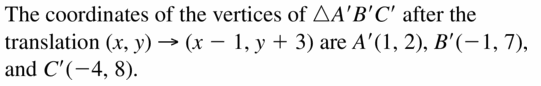
Question 54.
(x, y) → (x + 3, y – 1)
Answer:
translation: (x, y) → (x + 3, y – 1)
A(2, -1) → (x + 3, y – 1)
A(2, -1) → (2 + 3, -1 – 1) = A'(5, -2)
B(0, 4) → (x + 3, y – 1)
B(0, 4) → (0 + 3, 4 – 1) = B'(3, 3)
C(-3, 5) → (x + 3, y – 1)
C(-3, 5) → (-3 + 3, 5 – 1) = C'(0, 4)
Question 55.
(x, y) → (x – 2, y)
Answer:
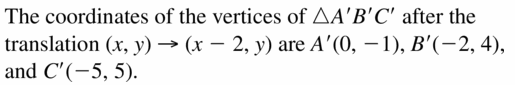
Question 56.
(x, y) → (x + 1, y – 2)
Answer:
(x, y) → (x – 2, y)
A(2, -1) → A'(3, -3)
B(0, 4) → B'(1, 2)
C(-3, 5) → C'(-2, 3)
Question 57.
(x, y) → (x – 3y + 1)
Answer:
4.6 Similarity and Transformations
Exploration 1
Dilations and similarity
Work with a partner.
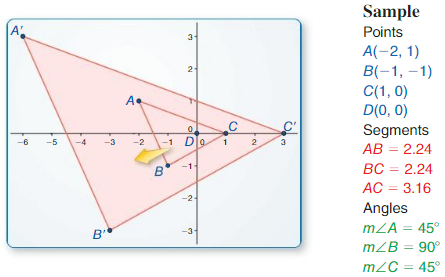
a. Use dynamic geometry software to draw any triangle and label it ∆ABC.
Answer:
We have a triangle ABC with vertices A(2, 1), B(1, 3) and C(3, 2).
The image of the graph of ΔABC along with its dilated figure by scale factor 2 that is ΔA’B’C’ are A'(4,2), B'(2, 6) and C'(6, 4)
Thus each coordinate of ΔA’B’C’ are twice than the coordinates of corresponding vertices ΔABC.
Also the side lengths of dilated image ΔA’B’C’ are double than the side lengths of the original image ΔABC.
But the measure of ∠A, ∠B and ∠C are same as the measure of ∠A’, ∠B’ and ∠C’ respectively.
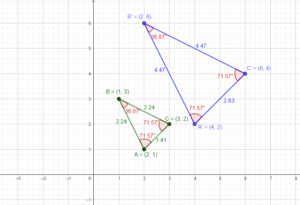
b. Dilate the triangle using a scale factor of 3. Is the image similar to the original triangle? Justify your answer.
ATTENDING TO PRECISION
To be proficient in math, you need to use clear definitions in discussions with others and in your own reasoning.
Answer:
We have a triangle ABC with vertices A(2, 1), B(1, 3) and C(3, 2).
The image of the graph of ΔABC along with its dilated figure by scale factor 1/2 that is ΔA”B”C”
It can be observed that the coordinates of ΔA”B”C” are A”(1, 0.5), B”(0.5, 1.5) and C”(1.5, 1)
Thus each coordinate of vertices ΔA”B”C” are half than the coordinates of corresponding vertices of ΔABC.
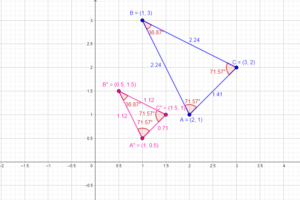
Exploration 2
Rigid Motions and Similarity
Work with a partner.
a. Use dynamic geometry software to draw any triangle.
Answer:
b. Copy the triangle and translate it 3 units left and 4 units up. Is the image similar to the original triangle? Justify your answer.
Answer:
c. Reflect the triangle in the y-axis. Is the image similar to the original triangle? Justify your answer.
Answer:
d. Rotate the original triangle 90° counterclockwise about the origin. Is the image similar to the original triangle? Justify your answer.
Answer:
Communicate Your Answer
Question 3.
When a figure is translated, reflected, rotated, or dilated in the plane, is the image always similar to the original figure? Explain your reasoning.
Answer:
When a figure is translated, reflected, rotated, or dilated in the plane, the image is always similar to the original figure.
Two figures are similar if and only if one figure can be obtained from the other by a single transformation, or a sequence of transformations, including translations, reflections, rotations, and/or dilations or equivalently corresponding angles are equal and sides are proportional.
Question 4.
A figure undergoes a composition of transformations. which includes translations.
reflections, rotations, and dilations. Is the image similar to the original figure?
Explain your reasoning.
Answer:
Translation:
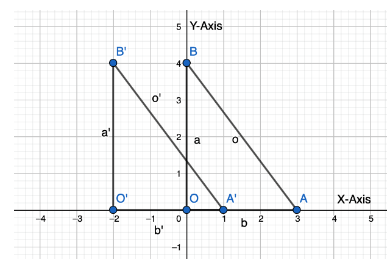
AB = A’B’
OA = O’A’
OB = O’B’
Rotation:
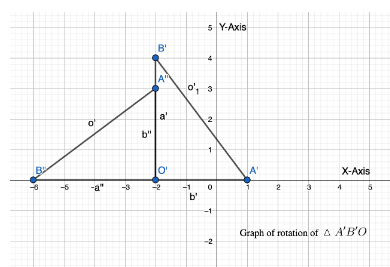
A”B” = A’B’
A”O” = A’O’
B”O” = B’O’
Reflection:
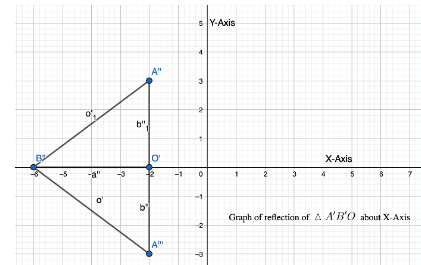
A”B” = A”‘B”
A”O” =’ = A”‘O’
B”O’ = B’O’
Since dilation is done by an amount of 3 units
A”‘B” = bA””B”‘
A”‘O’ = 3A””O’
B”O’ = 3B”‘O’
AB = 3A””B”‘
AO = 3A””O’
BO = 3B”‘O’
AB/A””B”‘ = AO/A””O’ = BO/B”‘O’
ΔABO is similar to ΔA””B”‘O’
Lesson 4.6 Similarity and Transformations
Monitoring Progress
Question 1.
Graph \(\overline{C D}\) with endpoints C(- 2, 2) and D(2, 2) and its image after the similarity transformation.
Rotation: 90° about the origin
Dilation: (x, y) → \(\left(\frac{1}{2} x, \frac{1}{2} y\right)\)
Answer:
Rotation: 90° about the origin
Dilation: (x, y) → \(\left(\frac{1}{2} x, \frac{1}{2} y\right)\)
C'(-2, -2)
D'(-2, 2)
C”(-1, -1)
D”(-1, 1)
Question 2.
Graph ∆FGH with vertices F(1, 2), G(4, 4), and H(2, 0) and its image after the similarity transformation.
Reflection: in the x-axis
Dilation: (x, y) → (1.5x, 1.5y)
Answer:
Reflection: in the x-axis is (-b, a)
Dilation: (x, y) → (1.5x, 1.5y)
F'(1, -2)
G'(4, -4)
H'(2, 0)
F”(1.5, -3)
G”(6, -6)
H”(3, 0)
Question 3.
In Example 2, describe another similarity transformation that maps trapezoid PQRS to trapezoid WXYZ.
Answer:
Sample answer: Reflection in the x-axis followed by a dilation with a scale factor of -1/3
Question 4.
Describe a similarity transformation that maps quadrilateral DEFG to quadrilateral STUV.
Answer:
Sample answer: dilation with a scale factor of 1/2 followed by a 180° rotation about the origin.
Question 5.
Prove that ∆JKL is similar to ∆MNP.
Given Right isosceles ∆JKL with leg length t, right isosceles ∆MNP with leg length ν,
\(\overline{L J}\) || \(\overline{P M}\)
Prove ∆JKL is similar to ∆MNP.
Answer:
\(\overline{L J}\) || \(\overline{P M}\)
According to the definition of translation, the original figure does not change any shape or size, it only moves in a particular direction.
So, the line segment KL maps the line segment NP of ∆MNP.
∠KLJ maps the ∠NPM as it is given that both the triangles are right isosceles triangles.
So, each angle measure 90 degrees.
dilation factor k = PM/PJ
The length of the line segment PM is v and the length of the line segment LJ is t.
k – PM/PJ
k = v/t
After applying the dilation, the line segment PJ maps PM and the line segment PK maps PN.
Therefore, on applying translation and dilation the given ∆JKL maps the ∆MNP.
So, ∆JKL is similar to ∆MNP.
Exercise 4.6 Similarity and Transformations
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
What is the difference between similar figures and congruent figures?
Answer:
Congruent figures have the same size and shape. Similar figures have the same shape, but not necessarily the same size.
Question 2.
COMPLETE THE SENTENCE
A transformation that produces a similar figure. such as a dilation.
is called a _________ .
Answer: A transformation that produces a similar figure. such as a dilation is called a similarity transformation.
Monitoring Progress and Modeling with Mathematics
In Exercises 3-6, graph ∆FGH with vertices F(- 2, 2), G(- 2, – 4), and H(- 4, – 4) and its image after the similarity transformation.
Question 3.
Translation: (x, y) → (x + 3, y + 1)
Dilation: (x, y) → (2x, 2y)
Answer:
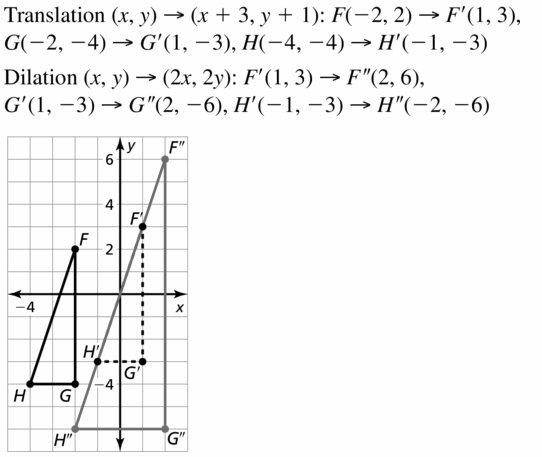
Question 4.
Dilation: (x, y) → \(\left(\frac{1}{2} x, \frac{1}{2} y\right)\)
Reflection: in the y-axis
Answer:
Dilation: (x, y) → \(\left(\frac{1}{2} x, \frac{1}{2} y\right)\)
F(-2, 2) → F'(-1, 1)
G(-2, -4) → G'(-1, -2)
H(-4, -4) → F'(-2, -2)
Reflection: in the y-axis
F'(-1, 1) → F”(1, 1)
G'(-1, -2) → G”(1, -2)
H'(-2, -2) → H”(2, -2)
Question 5.
Rotation: 90° about the origin
Dilation: (x, y) → (3x, 3y)
Answer:
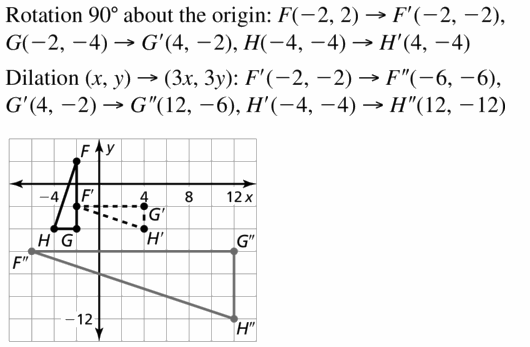
Question 6.
Dilation: (x, y) → \(\left(\frac{3}{4} x, \frac{3}{4} y\right)\)
Reflection: in the x-axis
Answer:
First draw ΔFGH with vertices F(-2, 2), G(-2, -4) and H(-4, -4)
Dilation: (x, y) → \(\left(\frac{3}{4} x, \frac{3}{4} y\right)\)
Scale factor is \(\frac{3}{4}\)
F(-2, 2) = F'(-\(\frac{3}{2}\), \(\frac{3}{2}\))
G(-2, -4) = G'(-\(\frac{3}{2}\), -3)
H(-4, -4) = H'(-3, -3)
Reflection: in the x-axis
F'(-\(\frac{3}{2}\), \(\frac{3}{2}\)) → F”(-\(\frac{3}{2}\), – \(\frac{3}{2}\))
G'(-\(\frac{3}{2}\), -3) → G”(-\(\frac{3}{2}\), 3)
H'(-3, -3) → H”(-3, 3)
In Exercises 7 and 8. describe a similarity transformation that maps the blue preimage to the green image.
Question 7.
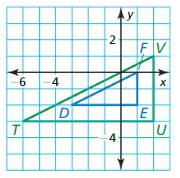
Answer:

Question 8.
Answer:
The similarity transformation that maps the blue preimage to green image is:
Reflection on y-axis. Then dilation with the scale factor is 1/2 about the center point (0, 0)
The length of \(\overline{J K}\) = 4 units
The length of \(\overline{J” K”}\) = 2 units
Scale factor =\(\overline{J” K”}\) / \(\overline{J K}\) = 2/4 = 1/2
In Exercises 9-12, determine whether the polygons with the given vertices are similar. Use transformations to explain your reasoning.
Question 9.
A6, 0), B(9, 6), C(12, 6) and D(0, 3), E( 1, 5), F(2. 5)
Answer:

Question 10.
Q(- 1, 0), R(- 2, 2), S(1, 3), T(2, 1) and W(0, 2), X(4, 4), Y(6, – 2), Z(2, – 4)
Answer:
The length of a segment with two points (x1, y1) and (x2, y2)
= √(y2 – y1)² + (x2 – x1)²
The length of \(\overline{R S}\) = √(3 – 2)² + (1 – (-2))²
= √1² + 3²
= √10
The length of \(\overline{X Y}\) = √(-2 – 4)² + (6 – 4)²
= √(-6)² + 2²
= √36 + 4 = √40
= 2 × √10
\(\overline{X Y}\) = 2 × \(\overline{R S}\)
The length of \(\overline{S T}\) = √(1 – 3)² + (2 – 1)²
= √4 + 1
= √5
The length of \(\overline{Y Z}\) = √(-4 – (-2))² + (2 – 6)²
= √(-2)² + (-4)²
= √4 + 16 = √20
= 2 × √5
\(\overline{Y Z}\) = 2 × \(\overline{S T}\)
So, Quadrilateral WXYZ is a symmetry transformation of Quadrilateral QRST with a scale factor 2.
By dilation quadrilateral QRST from the origin and with a scale factor of 2, we get the image Q’R’S’T’
Q'(-2, 0) → W(0, 2)
R'(-4, 4) → X(4, 4)
S'(2, 6) → Y(6, -2)
T'(4, 2) → Z(2, -4)
The symmetry transformation of the two figures is 270° rotation and silation with a scale factor of 2.
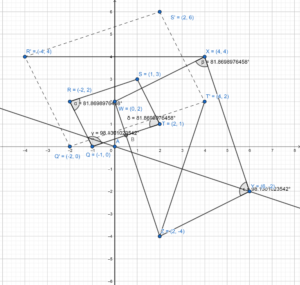
Question 11.
G(- 2, 3), H(4, 3), I(4, 0) and J(1, 0), K(6, – 2), L(1, – 2)
Answer:

Question 12.
D(- 4, 3), E(- 2, 3), F(- 1, 1), G(- 4, 1) and L(1, – 1), M(3, – 1), N(6, – 3), P(1, – 3)
Answer:
\(\overline{L P}\) = 2 units
\(\overline{D G}\) = 2 units
The ratio = 2/2 = 1
The long leg:
\(\overline{P N}\) = 5 units
\(\overline{G F}\) = 3 units
The ratio = 5/3
Since the ratio is not a constant, then the figures are not similar.
In Exercises 13 and 14, prove that the figures are similar.
Question 13.
Given Right isosceles ∆ABC with leg length j.
right isosceles ∆RST with leg length k.
\(\overline{C A}\) || \(\overline{R T}\)
Prove ∆ABC is similar to ∆RST.
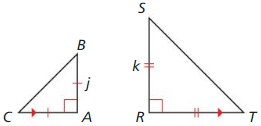
Answer:
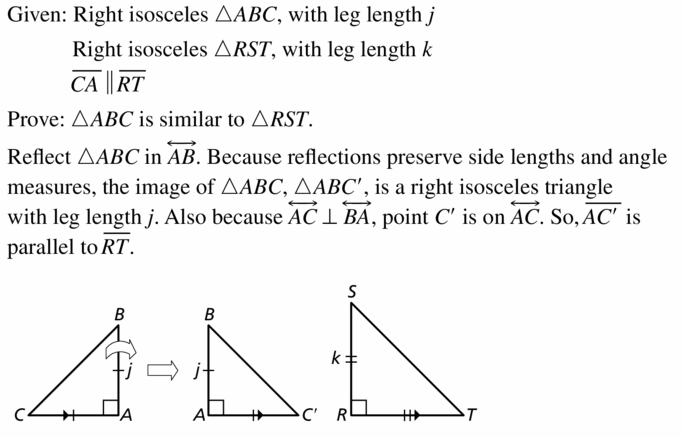
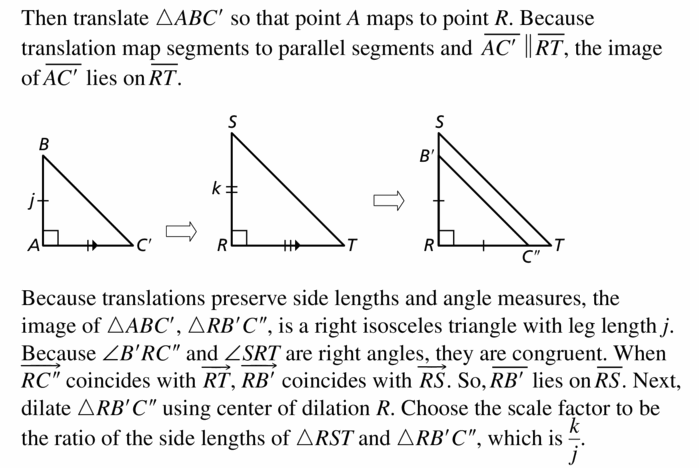
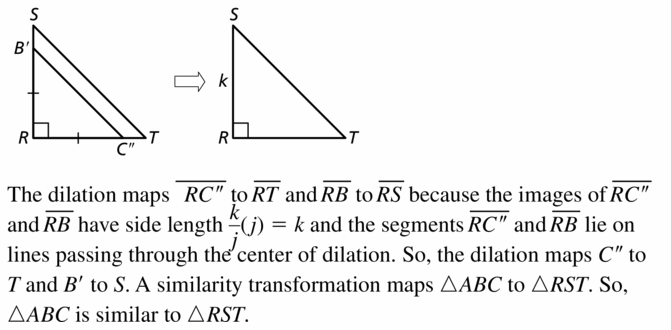
Question 14.
Given Rectangle JKLM with side lengths x and y, rectangle QRST with side lengths 2x and 2y
Prove Rectangle JKLM is similar to rectangle QRST.
Answer:
It can be seen that both the dimensions of QRST are 2 times that of JKLM and that they are both rectangles so the 2 rectangles must be similar.
QRST are 2y/y = 2x/x = 2 times larger than that of JKLM
Therefore the 2 rectangles are similar.
Question 15.
MODELING WITH MATHEMATICS
Determine whether the regular-sized stop sign and the stop sign sticker are similar. Use transformations to explain your reasoning.
Answer:

Question 16.
ERROR ANALYSIS
Describe and correct the error in comparing the figures.
Answer:
Two figures are similar if they are the same shape, if their corresponding angles are congruent, and the ratios of the lengths of their corresponding sides are equal.
Length of longer side of a figure A/Length of longer side of a figure B = 6/4 = 3/2
Length of shorter side of a figure A/Length of shorter side of a figure B = 4/2 = 2
When two figures are similar, the ratios of the lengths of their corresponding sides are equal, but this case the ratios of the lengths of their corresponding sides are not equal, so figure A and B are not similar.
Question 17.
MAKING AN ARGUMENT
A member of the homecoming decorating committee gives a printing company a banner that is 3 inches by 14 inches to enlarge. The committee member claims the banner she receives is distorted. Do you think the printing company distorted the image she gave it? Explain.

Answer:
No. The scale factor is 6 for both dimensions. So, the enlarged banner is proportional to the smaller one.
Question 18.
HOW DO YOU SEE IT?
Determine whether each pair of figures is similar. Explain your reasoning.
a.
Answer: The above figure is similar because the right sun can be obtained by shrinking the left sum.
b.

Answer:
Not similar, because both figures appear to have the same height, but the right heart appears to be wider than the left heart and thus it is not possible to obtain one of the hearts by shrinking one of the other hearts.
Question 19.
ANALYZING RELATIONSHIPS
Graph a polygon in a coordinate plane. Use a similarity transformation involving a dilation (where k is a whole number) and a translation to graph a second polygon. Then describe a similarity transformation that maps the second polygon onto the first.
Answer:

Question 20.
THOUGHT PROVOKING
Is the composition of a rotation and a dilation commutative? (In other words. do you obtain the same image regardless of the order in which you perform the transformations?) Justify your answer.
Answer:
Assuming we have a point A(a, b) on the coordinate plane.
Assuming the dilation and rotation center is the origin.
On dilating it with the scale factor k then rotating with 90° for instance.
Dilating first: A(a, b) → A'(ka, kb)
Then rotating 90°: A'(ka, kb) → A”(-kb, ka)
Question 21.
MATHEMATICAL CONNECTIONS
Quadrilateral JKLM is mapped to quadrilateral J’K’L’M’ using the dilation (x, y) → \(\left(\frac{3}{2} x, \frac{3}{2} y\right)\). Then quadrilateral J’K’L’M is mapped to quadrilateral J”K”L”M” using the translation (x, y) → (x + 3, y – 4). The vertices of quadrilateral J’K’L’M’ are J(- 12, 0), K(- 12, 18), L(- 6, 18), and M(- 6, 0), Find the coordinates of the vertices of quadrilateral JKLM and quadrilateral J”K”L”M”. Are quadrilateral JKLM and quadrilateral J”K”L”M” similar? Explain.
Answer:

Question 22.
REPEATED REASONING
Use the diagram.
a. Connect the midpoints of the sides of ∆QRS to make another triangle. Is this triangle similar to ∆QRS? Use transformations to support your answer.
Answer:
The midpoints of the line segments are algebraically evaluated using midpoint formula and triangle ABC is plotted.
It can be seen that the 2 triangles are similar as the corresponding side lengths of ABC are half in length of that QRS.
b. Repeat part (a) for two other triangles. What conjecture can you make?
Answer:

The midpoints of the line segments are algebraically evaluated using midpoint formula and triangle STU is plotted.
It can be seen that the 2 triangles are similar as the corresponding side lengths of STU are half in length of that MNP.
The midpoints of the line segments are algebraically evaluated using midpoint formula and triangle EFG is plotted.
It can be seen that the 2 triangles are similar as the corresponding side lengths of EFG are half in length of that KLM.
The triangle formed inside a bigger triangle by joining the midpoints of the line segments bigger triangle is also similar to the bigger triangle.
Maintaining Mathematical Proficiency
Classify the angle as acute, obtuse, right, or straight.
Question 23.
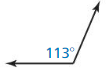
Answer:
![]()
Question 24.
![]()
Answer: Straight angle
Question 25.
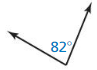
Answer:
![]()
Question 26.
Answer: Right angle
Transformations Chapter Review
4.1 Translations
Graph ∆XYZ with vertices X(2, 3), Y(- 3, 2), and Z(- 4, – 3) and its image after the translation.
Question 1.
(x, y) → (x, y + 2)
Answer:
Given,
(x, y) → (x, y + 2)
(2, 3) → (2, 3 + 2)
(2, 3) → (2, 5)
x = -3 and y = 2 in the translation to find Y’
(x, y) → (x, y + 2)
(-3, 2) → (-3, 2 + 2)
(-3, 2) → (-3, 4)
x = -3 and y = 2 in the translation to find Z’
(x, y) → (x, y + 2)
(-4, -3) → (-4, -3 + 2)
(-4, -3) → (-4, -1)
Then we will graph the triangle X’Y’Z’ with vertices X'(2, 5), Y'(-3, 4) and Z'(-4, -1)
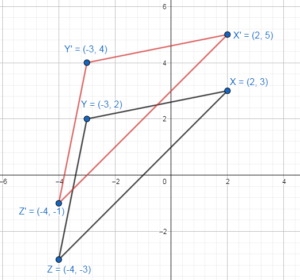
Question 2.
(x, y) → (x – 3, y)
Answer:
Given,
(x, y) → (x – 3, y)
Substitute x = 2 and y = 3 in the translation to find X’
(2, 3) → (2 – 3, 3)
(2, 3) → (-1, 3)
Substitute x = -3 and y = 2 in the translation to find Y’
(x, y) → (x – 3, y)
(-3, 2) → (-3 – 3, 2)
(-3, 2) → (-6, 2)
Substitute x = -4 and y = -3 in the translation to find Z’
(x, y) → (x – 3, y)
(-4, -3) → (-4 – 3, -3)
(-4, -3) → (-7, -3)
Then we will graph the triangle X’Y’Z’ with vertices X'(-1, 3), Y'(-6, 2) and Z'(-7, -3)
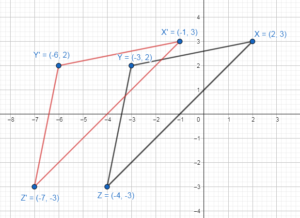
Question 3.
(x, y) → (x + 3, y – 1)
Answer:
Given,
(x, y) → (x + 3, y – 1)
Substitute x = 2 and y = 3 in the translation to find X’
(x, y) → (x + 3, y – 1)
(2, 3) → (2 + 3, 3 – 1)
(2, 3) → (5, 2)
Substitute x = -3 and y = 2 in the translation to find Y’
(x, y) → (x + 3, y – 1)
(-3, 2) → (-3 + 3, 2 – 1)
(-3, 2) → (0, 1)
Substitute x = -4 and y = -3 in the translation to find Z’
(x, y) → (x + 3, y – 1)
(-4, -3) → (-4 + 3, -3 – 1)
(-4, -3) → (-1, -4)
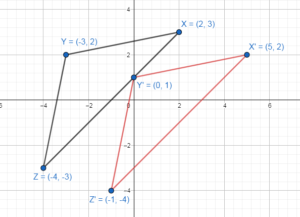
Question 4.
(x, y) → (x + 4, y + 1)
Answer:
Given,
(x, y) → (x + 4, y + 1)
Substitute x = 2 and y = 3 in the translation to find X’
(x, y) → (x + 4, y + 1)
(2, 3) → (2 + 4, 3 + 1)
(2, 3) → (6, 4)
Substitute x = -3 and y = 2 in the translation to find Y’
(x, y) → (x + 4, y + 1)
(-3, 2) → (-3 + 4, 2 + 1)
(-3, 2) → (1, 3)
Substitute x = -4 and y = -3 in the translation to find Z’
(x, y) → (x + 4, y + 1)
(-4, -3) → (-4 + 4, -3 + 1)
(-4, -3) → (0, -2)
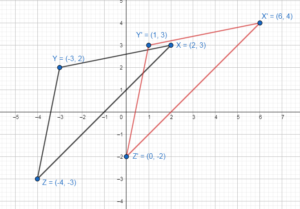
Graph ∆PQR with vertices P(0, – 4), Q(1, 3), and R(2, – 5) and its image after the composition.
Question 5.
Translation: (x, y) → (x + 1, y + 2)
Translation: (x, y) → (x – 4, y + 1)
Answer:
Substitute x = 0 and y = -4 from point P(0, -4) in the translation to find P’
(x, y) → (x + 1, y + 2)
(0, -4) → (0 + 1, -4 + 2)
(0, -4) → (1, -2)
Substitute x = 1 and y = 3 from point Q(1, 3) in the translation to find Q’
(x, y) → (x + 1, y + 2)
(1, 3) → (1 + 1, 3 + 2)
(1, 3) → (2, 5)
Substitute x = 2 and y = -5 from point R(2, -5) in the translation to find R’
(x, y) → (x + 1, y + 2)
(2, -5) → (2 + 1, -5 + 2)
(2, -5) → (3, -3)
P’Q’R’ with vertices P(1, -2), Q'(2, 5) and R'(3, -3)
Translation: (x, y) → (x – 4, y + 1)
Substitute x = 1 and y = -2 from point P'(1, -2) in the translation to find P”
(x, y) → (x – 4, y + 1)
(1, -2) → (1 – 4, -2 + 1)
(1, -2) → (-3, -1)
Substitute x = 2 and y = 5 from point Q'(2, 5) in the translation to find Q”
(x, y) → (x – 4, y + 1)
(2, 5) → (2 – 4, 5 + 1)
(2, 5) → (-2, 6)
Substitute x = 3 and y = -3 from point R'(3, -3) in the translation to find R”
(x, y) → (x – 4, y + 1)
(3, -3) → (3 – 4, -3 + 1)
(3, -3) → (-1, -2)
P”Q”R” with vertices P”(-3, -1), Q”(-2, 6) and R”(-1, -2)
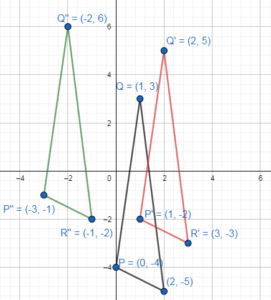
Question 6.
Translation: (x, y) → (x, y + 3)
Translation: (x, y) → (x – 1, y + 1)
Answer:
Given,
Translation: (x, y) → (x, y + 3)
x = 0 and y = -4 from P(0, -4) in the translation to find P1
(x, y) → (x, y + 3)
(0, -4) → (0, -4 + 3)
(0, -4) → (0, -1)
Substitute x = 1 and y = 3 from point Q(1, 3) in the translation to find Q’
(x, y) → (x, y + 3)
(1, 3) → (1, 3 + 3)
(1, 3) → (1, 6)
Substitute x = 2 and y = -5 from point R(2, -5) in the translation to find R’
(x, y) → (x, y + 3)
(2, -5) → (2, -5 + 3)
(2, -5) → (2, -2)
P’Q’R’ with vertices P(0, -1), Q'(1, 6) and R'(2, -2)
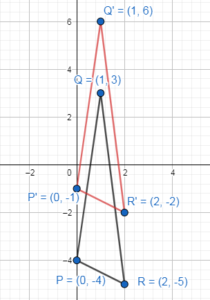
Substitute x = 0 and y = -1 from point P'(0, -1) in the translation to find P”
Translation: (x, y) → (x – 1, y + 1)
(x, y) → (x – 1, y + 1)
(0, -1) → (0 – 1, -1 + 1)
(0, -1) → (-1, 0)
Substitute x =1 and y = 6 from point Q'(1, 6) in the translation to find Q”
(x, y) → (x – 1, y + 1)
(1, 6) → (1 – 1, 6 + 1)
(1, 6) → (0, 7)
Substitute x = 2 and y = -2 from point R'(2, -2) in the translation to find R”
(x, y) → (x – 1, y + 1)
(2, -2) → (2 – 1, -2 + 1)
(2, -2) → (1, -1)
P”Q”R” with vertices P”(-1, 0), Q”(0, 7) and R”(1, -1)
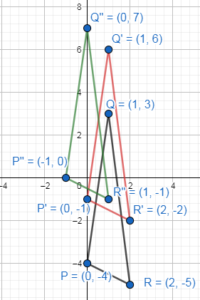
4.2 Reflections
Graph the polygon and its image after a reflection in the given line.
Question 7.
x = 4
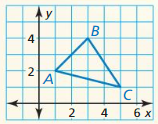
Answer:
x = 4 to the triangle ABC.
We will find a point A’
The coordinates of this point are A'(7, 2)
Find B’:
The coordinates of this point are B'(5, 4)
Find C’:
The coordinates of this point are C'(3, 1)
When the point is reflect in the line x = 4 the x-coordinate changes, the y-coordinate remains the same.
A'(7, 2), B'(5, 4) and C'(3, 1)
Question 8.
y = 3
Answer:
y = 3 to the triangle EFGH.
We will find a point E’
The coordinates of this point are E'(1, 3)
Find F’:
The coordinates of this point are F'(4, 3)
Find G’:
The coordinates of this point are G'(5, 6)
Find H’:
The coordinates of this point are H'(2, 6)
E’ and F’ have the same coordinate like points E and F.
E’F’G’H’ with vertices E'(1, 3), F'(4, 3), G'(5, 6) and H'(2, 6)
Question 9.
How many lines of symmetry does the figure have?
Answer: The above figure has 2 lines of symmetry.
4.3 Rotations
Question 10.
A(- 3, – 1), B(2, 2), C(3, – 3); 90°
Answer:
A(-3, -1) through an angle 90° about the origin, we will get the point A'(1, -3)
B(2, 2) through an angle 90° about the origin, we will get the point B'(-2, 2)
C(3, -3) through an angle 90° about the origin, we will get the point C'(3, 3)
Graph the polygon A’B’C’ with the vertices A'(1, -3), B'(-2, 2) and C'(3, 3)
Question 11.
W(- 2, – 1), X(- 1, 3), Y(3, 3), Z(3, – 3); 180°
Answer:
Given the vertices
W(- 2, – 1), X(- 1, 3), Y(3, 3), Z(3, – 3); 180°
Now you have to rotate W(2, 1) through an angle 180° about the origin, we will get the point W'(2, 1)
We will also X(1, 3) through an angle 180° about the origin, we will get the point X'(1, -3)
We will also Y(3, 3) through an angle 180° about the origin, we will get the point Y'(-3, -3)
At the end we will rotate Z(3, 3) through an angle 180° about the origin, we will get the point Z'(-3, 3)
The x-coordinates of new points change sign, the y-coordinate of new points change sign.
W'(2, 1), X'(1, -3), Y'(-3, -3), Z'(-3, 3)
Question 12.
Graph \(\overline{X Y}\) with endpoints X(5, – 2) and Y(3, – 3) and its image after a reflection in the x-axis and then a rotation of 270° about the origin.
Answer:
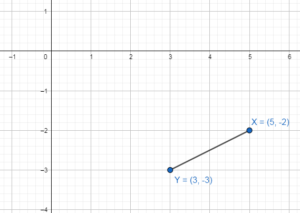
Now we will apply reflection in the x-axis to the \(\overline{X Y}\)
We will find the point X’ which is in the same place on the opposite sides x-axis with respect to the point X.
The coordinates of this point are X'(5, 2)
We will find the point Y’ which is in the same place on the opposite sides x-axis with respect to the point Y.
The coordinates of this point are Y'(3, 3)
Graph \(\overline{X’ Y’}\) with end points X'(5, 2) and Y'(3, 3)
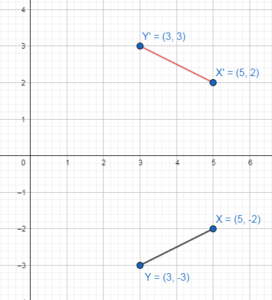
Determine whether the figure has rotational symmetry. If so, describe any rotations that map the figure onto itself.
Now we have to rotate X'(5, 2) through an angle 270° about the origin, we will get the point X”(2, -5)
Now we have to rotate Y'(3, 3) through an angle 270° about the origin, we will get the point Y”(3, -3)
Graph \(\overline{X” Y”}\) with end points X”(2, -5) and Y”(3, -3)
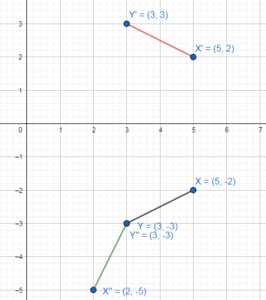
Question 13.

Answer:
The above figure has 6 rotations that can map the figure onto itself.
Question 14.
Answer:
A pentagon has a rotational symmetry.
It has 5 rotations that can map the figure onto itself.
4.4 Congruence and Transformations
Describe a congruence transformation that maps ∆DEF to ∆JKL.
Question 15.
D(2, – 1), E(4, 1), F(1, 2) and J(- 2, – 4), K(- 4, – 2), L(- 1, – 1)
Answer:
Graphing ∆DEF and ∆JKL.
On reflecting ∆DEF on y-axis, we obtain ∆D’E’F’ with the vertices.
D(-2, – 1), E(-4, 1), F(-1, 2)
On translating ∆D’E’F’ 3 units down
D'(-2, – 1) → D”(-2, -4) ≅ J
E'(-4, 1) → E”(-4, -2) ≅ K
F'(-1, 2) → F”(-1, -1) ≅ L
The congruence transformation that maps ∆DEF and ∆JKL is reflecting on the y-axis. then translating 3 units downwards.
Question 16.
D(- 3, – 4), E(- 5, – 1), F(- 1, 1) and J(1, 4), K(- 1, 1), L(3, – 1)
Answer:
Graphing ∆DEF and ∆JKL.
On reflecting ∆DEF on y-axis, we obtain ∆D’E’F’ with the vertices.
D'(- 3, 4), E'(- 5, 1), F'(- 1, -1)
On translating ∆D’E’F’ 3 units down
D'(-3, 4) → D”(1, 4) ≅ J
E'(-5, 1) → E”(-1, 1) ≅ K
F'(-1, -1) → F”(3, -1) ≅ L
The congruence transformation that maps ∆DEF and ∆JKL is reflecting on the y-axis. then translating 4 units right.
Question 17.
Which transformation is the same as reflecting an object in two Parallel lines? in two intersecting lines?
Answer:
Reflection in 2 parallel lines can be represented by a single translation of the preimage to form the image.
Reflection in 2 intersecting lines can be represented by a single rotation of preimage to form the image about the point of intersecting of the 2 lines and through the angle twice that of angle between 2 intersecting lines.
4.5 Dilations
Graph the triangle and its image after a dilation with scale factor k.
Question 18.
P(2, 2), Q(4, 4), R(8, 2); k = \(\frac{1}{2}\)
Answer:
dilation (x, y) → (\(\frac{1}{2}\)x, \(\frac{1}{2}\)y)
P(2, 2), Q(4, 4), R(8, 2)
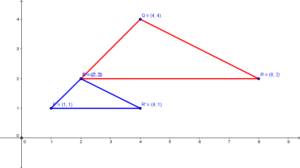
Question 19.
X(- 3, 2), Y(2, 3), Z(1, – 1); k = – 3
Answer:
We need to use the coordinate rule for dilation with scale factor k = -3 to find the coordinates of the vertices.
(x, y) → (-3x, -3y)
X(-3, 2) → X'(-3 . (-3), -3 . 2) = X'(9, -6)
Y(2, 3) → Y'(-3 . 2, -3 . 3) = Y'(-6, -9)
Z(1, -1) → Z'(-3 . 1, -3 . (-1)) = Z'(-3, 3)
Question 20.
You are using a magnifying glass that shows the image of an object that is eight times the object’s actual size. The image length is 15.2 centimeters. Find the actual length of the object.
Answer:
Given,
You are using a magnifying glass that shows the image of an object that is eight times the object’s actual size.
The image length is 15.2 centimeters.
15.2/8 = 1.9 centimeters
4.6 Similarity and Transformations
Describe a similarity transformation that maps ∆ABC to ∆RST.
Question 21.
A(1, 0), B(- 2, – 1), C(- 1, – 2) and R(- 3, 0), S(6, – 3), T(3, – 6)
Answer:
\(\overline{A C}\) = √(-2 – 0)² + (-1 – 1)² = √8 = 2 × √2
\(\overline{R T}\) = √(-6 – 0)² + (3 – (-3))² = √72 = 6 × √2
The ratio \(\overline{R T}\)/\(\overline{A C}\) = 6 × √2/2 × √2 = 3
\(\overline{B C}\) = √(-2 + 1)² + (-1 + 2)² = √2
\(\overline{S T}\) = √(-6 + 3)² + (3 – 6)² = √18 = 3 × √2
The ratio \(\overline{S T}\)/\(\overline{B C}\) = 3 × √2/ √2 = 3
\(\overline{A B}\) = √(-1 – 0)² + (-2 – 1)² = √10
\(\overline{R S}\) = √(-3 – 0)² + (6 + 3)² = √90= 3 × √10
The ratio \(\overline{R S}\)/\(\overline{A B}\) = 3 × √10/ √10 = 3
∆RST is a dilation of ∆ABC with a scale factor 3.
By dilating ∆ABC with a scale factor of 3
A(1, 0) → A'(3, 0)
B(-2, -1) → B'(-6, -3)
C(-1, -2) → C'(-3, -6)
On reflecting ∆A’B’C’ about the y-axis:
A'(3, 0) → A”(-3, 0) ≅ R
B'(-6, -3) → B”(6, -3) ≅ S
C'(-3, -6) → C”(3, -6) ≅ T
The similarity transformation that maps ∆ABC to ∆RST is dilating with a scale factor of 3.
Question 22.
A(6, 4), B(- 2, 0), C(- 4, 2) and R(2, 3), S(0, – 1), T(1, – 2)
Answer:
\(\overline{A B}\) = √(0 – 4)² + (-2 – 6)² = √80 = 4 × √5
\(\overline{R S}\) = √(-1 – 3)² + (0 – 2)² = √20 = 2 × √5
The ratio \(\overline{R S}\)/\(\overline{A B}\) = 2 × √5/4 × √5 = 1/2
\(\overline{B C}\) = √(2 – 0)² + (-4 + 2)² = √8 = 2 × √2
\(\overline{S T}\) = √(-2 + 1)² + (1 – 0)² = √2
The ratio \(\overline{S T}\)/\(\overline{B C}\) =√2/ 2 × √2 = 1/2
\(\overline{A C}\) = √(2 – 4)² + (-4 – 6)² = √104 = 2 × √26
\(\overline{R T}\) = √(-2 – 3)² + (1 – 2)² = √26
The ratio \(\overline{R T}\)/\(\overline{A C}\) =√26 / 2 × √26 = 1/2
∆RST is a dilation of ∆ABC with a scale factor 1/2
By dilating ∆ABC with a scale factor of 1/2
A(6, 4) → A'(3, 2)
B(-2, 0) → B'(-1, 0)
C(-4, 2) → C'(-2, 1)
On reflecting ∆A’B’C’ about the line y = x
A'(3, 2) → A”(-3, 0) ≅ R
B'(-1, 0) → B”(0, -1) ≅ S
C'(-2, 1) → C”(1, -2) ≅ T
The similarity transformation that maps ∆ABC to ∆RST is dilating with a scale factor of 1/2
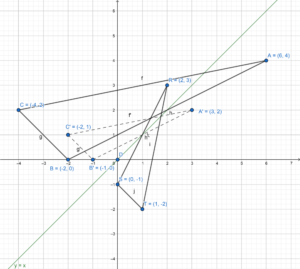
Question 23.
A(3, – 2), B(0, 4), C(- 1, – 3) and R(- 4, – 6), S(8, 0), T(- 6, 2)
Answer:
\(\overline{A B}\) = √(4 + 2)² + (0 – 3)² = √45 = 3 × √5
\(\overline{R S}\) = √(0 + 6)² + (8 + 4)² = √180 = 6 × √5
The ratio \(\overline{R S}\)/\(\overline{A B}\) = 6 × √5/3 × √5 = 2
\(\overline{B C}\) = √(-3 – 4)² + (-1 – 0)² = √50 = 5 × √2
\(\overline{S T}\) = √(2 – 0)² + (-6 – 8)² = √200 = 10 × √2
The ratio \(\overline{S T}\)/\(\overline{B C}\) =10 × √2/ 5 × √2 = 2
\(\overline{A C}\) = √(-3 + 2)² + (-1 – 3)² = √17
\(\overline{R T}\) = √(2 + 6)² + (-6 + 4)² = √68 = 2 × √17
The ratio \(\overline{R T}\)/\(\overline{A C}\) =2 × √17 / √17 = 2
∆RST is a dilation of ∆ABC with a scale factor 2
By dilating ∆ABC with a scale factor of 2
A(3, 2) → A'(-2, -3)
B(0, 4) → B'(4, 0)
C(-1, -3) → C'(-3, 1)
On reflecting ∆A’B’C’ about the line y = x
A'(-2, -3) → A”(-4, -6) ≅ R
B'(4, 0) → B”(8, 0) ≅ S
C'(-3, 1) → C”(-6, 2) ≅ T
The similarity transformation that maps ∆ABC to ∆RST is dilating with a scale factor of 2.
Transformations Test
Graph ∆RST with vertices R(- 4, 1), S(- 2, 2), and T(3, – 2) and its image after the translation.
Question 1.
(x, y) → (x – 4, y + 1)
Answer:
Given,
(x, y) → (x – 4, y + 1)
Substitute x = -4 and y = 1 in the translation to find R’
(x, y) → (x – 4, y + 1)
(-4, 1) → (-4 – 4, 1 + 1)
(-4, 1) → (-8, 2)
Substitute x = -2 and y = 2 in the translation to find S’
(x, y) → (x – 4, y + 1)
(-2, 2) → (-2 – 4, 2 + 1)
(-2, 2) → (-6, 3)
Substitute x = 3 and y = -2 in the translation to find T’
(x, y) → (x – 4, y + 1)
(3, -2) → (3 – 4, -2 + 1)
(3, -2) → (-1, -1)
R'(-8, 2), S'(-6, 3) and T'(-1, -1)
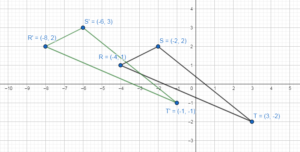
Question 2.
(x, y) → (x + 2, y – 2)
Answer:
Given,
(x, y) → (x + 2, y – 2)
Substitute x = -4 and y = 1 in the translation to find R’
(x, y) → (x + 2, y – 2)
(-4, 1) → (-4 + 2, 1 – 2)
(-4, 1) → (-2, -1)
Substitute x = -2 and y = 2 in the translation to find S’
(x, y) → (x + 2, y – 2)
(-2, 2) → (-2 + 2, 2 – 2)
(-2, 2) → (0, 0)
Substitute x = 3 and y = -2 in the translation to find T’
(x, y) → (x + 2, y – 2)
(3, -2) → (3 + 2, -2 – 2)
(3, -2) → (5, -4)
R’S’T’ with vertices R'(-2, -1), S'(0, 0) and T'(5, -4)
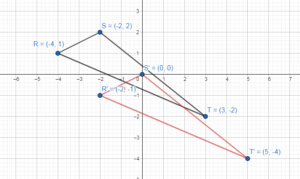
Graph the polygon with the given vertices and its image after a rotation of the given number of degrees about the origin.
Question 3.
D(- 1, – 1), E(- 3, 2), F(1, 4); 270°
Answer:
Rotate D(-1, -1) through an angle 270° about the origin we get D'(-1, 1)
Rotate E(-3, 2) through an angle 270° about the origin we get E'(2, 3)
Rotate F(1, 4) through an angle 270° about the origin we get F'(4, -1)
D'(-1, 1), E'(2, 3) and F'(4, -1)
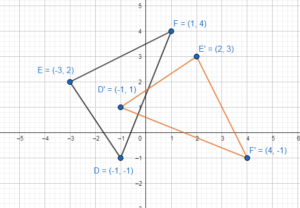
Question 4.
J(- 1, 1), K(3, 3), L(4, – 3), M(0, – 2); 90°
Answer:
Given,
J(- 1, 1), K(3, 3), L(4, – 3), M(0, – 2); 90°
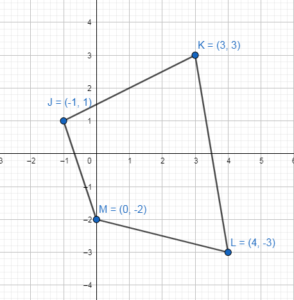
Rotate J(-1, 1) through an angle 90° about the origin we get J'(-1, -1)
Rotate K(3, 3) through an angle 90° about the origin we get K'(-3, 3)
Rotate L(4, -3) through an angle 90° about the origin we get L'(3, 4)
Rotate M(0, -2) through an angle 90° about the origin we get M'(2, 0)
J'(-1, -1), K'(-3, 3), L'(3, 4) and M'(2, 0)
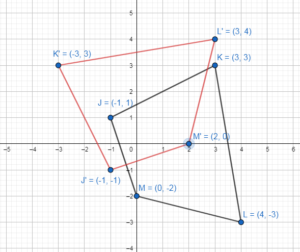
Determine whether the polygons with the given vertices are congruent or similar. Use transformations to explain your reasoning.
Question 5.
Q(2, 4), R(5, 4), S(6, 2), T(1, 2) and W(6, – 12), X(15, – 12), Y(18, – 6), Z(3, -,6)
Answer:
First we will graph the given points QRST and WXYZ
Q(2, 4), R(5, 4), S(6, 2), T(1, 2) and W(6, – 12), X(15, – 12), Y(18, – 6), Z(3, -,6)
k = 15/5
k = 3
Thus the scale factor is 3.
(x, y) → (3x, 3y)
x = 2 and y = 4 from point Q(2, 4) in the translation to find the Q’
(x, y) → (3x, 3y)
(2, 4) → (3(2), 3(4))
(2, 4) → (6, 12)
x = 5 and y = 4 from point R(5, 4) in the translation to find the R’
(x, y) → (3x, 3y)
(5, 4) → (3(5), 3(4))
(5, 4) → (15, 12)
x = 6 and y = 2 from point S(6, 2) in the translation to find the S’
(x, y) → (3x, 3y)
(6, 2) → (3(6), 3(2))
(6, 2) → (18, 6)
x = 1 and y = 2 from point T(1, 2) in the translation to find the T’
(x, y) → (3x, 3y)
(1, 2) → (3(1), 3(2))
(1, 2) → (3, 6)
Q'(6, 12), R'(15, 12), S'(18, 6) and T'(3, 6)
Now find Q” which is in the same place on opposite sides x-axis with respect to the point Q’.
The coordinates of this point are Q”(6, -12)
Now find R” which is in the same place on opposite sides x-axis with respect to the point R’.
The coordinates of this point are R”(15, -12)
Now find S” which is in the same place on opposite sides x-axis with respect to the point S’.
The coordinates of this point are S”(18, -6)
Now find T” which is in the same place on opposite sides x-axis with respect to the point T’.
The coordinates of this point are T”(3, -6)
Q”(6, -12), R”(15, -12), S”(18, -6) and T”(3, -6)
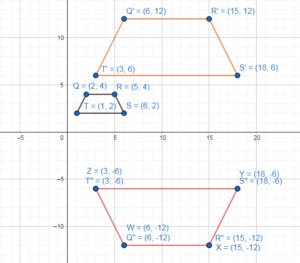
The sides of polygons WXYZ and QRST do not have equal length.
WXYZ and QRST are not congruent they are similar.
Question 6.
A(- 6, 6), B(- 6, 2), C(- 2, – 4) and D(9, 7), E(5, 7), F(- 1, 3)
Answer:
Given,
A(- 6, 6), B(- 6, 2), C(- 2, – 4) and D(9, 7), E(5, 7), F(- 1, 3)
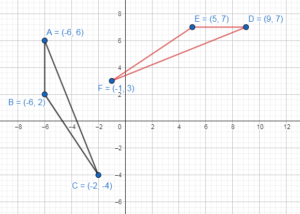
Rotate A(-6, 6) through an angle 270° about the origin, we will get the point A'(6, 6)
Rotate B(-6, 2) through an angle 270° about the origin, we will get the point B'(2, 6)
Rotate C(-2, -4) through an angle 270° about the origin, we will get the point C'(-4, 2)
A'(6, 6), B'(2, 6) and C'(-4, 2)
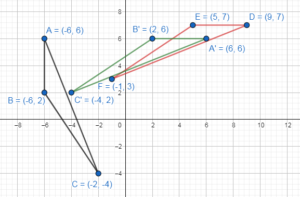
(x, y) → (x + 3, y + 1)
x = 6 and y = 6 from point A'(6, 6) in the translation to find A”
(x, y) → (x + 3, y + 1)
(6, 6) → (6 + 3, 6 + 1) = (9, 7)
x = 2 and y = 6 from point B'(2, 6) in the translation to find B”
(x, y) → (x + 3, y + 1)
(2, 6) → (2 + 3, 6 + 1) = (5, 7)
x = -4 and y = 2 from point C'(-4, 2) in the translation to find C”
(x, y) → (x + 3, y + 1)
(-4, 2) → (-4 + 3, 2 + 1) = (-1, 3)
A”(9, 7), B”(5, 7) and C”(-1, 3)
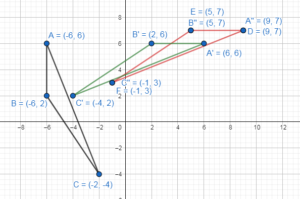
Determine whether the object has line symmetry and whether it has rotational symmetry.
Identify all lines of symmetry and angles of rotation that map the figure onto itself.
Question 7.

Answer:
It can be cut one directly down the middle from the top and from the side. It has rotational symmetry when rotated 180°
2 lines of symmetry and yes it has rotation symmetry.
Question 8.

Answer:

Question 9.

Answer:
The above figure is a four of diamond and because of the 4 written on it the figure has no line of symmetry by a rotational symmetry of 180° about the center of the card.
Question 10.
Draw a diagram using a coordinate plane. two parallel lines, and a parallelogram that demonstrates the Reflections in Parallel Lines Theorem (Theorem 4.2).
Answer:
If AB and CD are parallel, then a reflection in AB followed by a reflection in CD is the same as a translation.
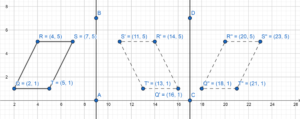
QRST can be translated 16 units right to construct Q”R”S”T”
Question 11.
A rectangle with vertices W(- 2, 4), X(2, 4), Y(2, 2), and Z(- 2, 2) is reflected in the y-axis. Your friend says that the image. rectangle W’X’ Y’Z. is exactly the same as the preimage. Is your friend correct? Explain your reasoning.
Answer:
Reflection is a transformation that does not affect the shape or size of an image with respect to its preimage, therefore, the friend is correct as WXYZ and W’X’Y’Z’ will be the same in shape and size.
Question 12.
Write a composition of transformations that maps ∆ABC Onto ∆CDB in the tesselation shown. Is the composition a congruence transformation? Explain your reasoning.
Answer:
The composition of transformation the maps ∆ABC Onto ∆CDB is reflecting ∆ABC on the x-axis.
Then translating its image with the rule
(a, b) → (a + 1, b + 2)
Question 13.
There is one slice of a large pizza and one slice of a small pizza in the box.
a. Describe a similarity transformation that maps pizza slice ABC to pizza slice DEF.
Answer:
Rule of given dilation is (x, y) → (1/2x, 1/b2y)
A(0, 0) → A'(0, 0)
B(2, 4) → B'(1, 2)
C(4, 2) → C'(2, 1)
The second similarity transformation is reflection across x-axis.
A'(0, 0) → A”(0, 0)
B'(1, 2) → B”(1, -2)
C'(2, 1) → C”(2, -1)
b. What is one possible scale factor for a medium slice of pizza? Explain your reasoning.
Answer:
If we use a dilation of a scale factor of 1/2 we will get a small pizza slice.
Thus a medium slice of pizza we will get if we use a dilation of a scale factor k which is in between 1 and 1/2.
This means the following inequality must apply
1/2 < k < 1
1/2 < k < 2/2
k = 1.5/2 = 3/4
Question 14.
The original photograph shown is 4 inches by 6 inches.

a. What transformations can you use to produce the new photograph?
Answer:
There are 2 types of transformations
1. Enlargement
2. Reflection on the vertical axis
b. You dilate the original photograph b a scale factor of \(\frac{1}{2}\). What are the dimensions of the new photograph?
Answer:
New dimension = scale factor . old dimension
4 . 1/2 = 2 and 6 . 1/2 = 3
Dimensions of new photograph: 2 inches by 3 inches
c. YOU have a frame that holds photos that are 8.5 inches by 11 inches. Can you dilate the original photograph to fit the frame? Explain your reasoning.
Answer:
8.5/4 = 2.125 and 11/6 = 1.833
Since the scale factors for both the dimensions are different, it will not be possible to dilate the photo to fit the frame.
Transformations Cumulative Assessment
Question 1.
Which composition 0f transformations maps ∆ABC to ∆DEF?
(A) Rotation: 90° counterclockwise about the origin
Translation: (x, y) → (x + 4, y – 3)
(B) Translation: (x, y) → (x – 4, y – 3)
Rotation: 90° counterclockwise about the origin
(C) Translation: (x, y) → (x + 4, y – 3)
Rotation: 90° counterclockwise about the origin
(b) Rotation: 90° counterclockwise about the origin
Translation: (x, y) → (x – 4, y – 3)
Answer: Option B is correct answer
Explanation:
The ΔABC with vertices A(-1, 2), B(3, 4) and C(2, 2).
(x, y) → (x – 4, y – 3)
(-1, 2) → (-1 – 4, 2 – 3) = (-5, -1)
x = 3 and y = 4 from point B(3, 4) in the translation to find B’
(x, y) → (x – 4, y – 3)
(3, 4) → (3 – 4, 4 – 3) = (-1, 1)
x = 2 and y = 2 from point C(2, 2) in the translation to find C’
(x, y) → (x – 4, y – 3)
(2, 2) → (2 – 4, 2 – 3) = (-2, -1)
Rotate A’ through an angle 90° about the origin, we will get the point D(1, -5)
Rotate B’ through an angle 90° about the origin, we will get the point E(-1, -1)
Rotate C’ through an angle 90° about the origin, we will get the point F(1, -2)
Thus the correct answer is option B.
Question 2.
Use the diagrams to describe the steps you would take to construct a line perpendicular to line m through point P. which is not on line m.
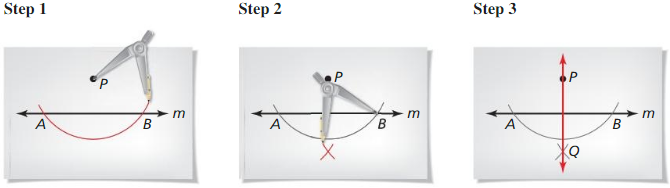
Answer:
Step 1: The fixed end of the compass is placed on P and an arc is drawn through the given line such that this intersects the given line at 2 points, A and B such that A and B are equidistant from P.
Measure this distance A and B, open the compass to a length greater than half of AB.
Place the fixed end at A and mark an ac below the given line.
Step 2: Without changing the length of the compass, move the fixed end to B and mark another arc below the given line. This point is labeled Q.
Step 3: Join P and Q by a straight line. Here PQ is perpendicular to the given line.
Question 3.
Your friend claims that she can find the perimeter of the school crossing sign without using the Distance Formula. Do you support your friend’s claim? Explain your reasoning.
Answer:
It can be seen that each unit here is equal to 1 unit.
Therefore the straight-lined perimeter can be evaluated by counting the number of boxes.
E = C = 2 units
D = 4 units
A = B and these form the hypotenuse of right isosceles triangles with side lengths of 2 units.
Therefore A = B = 2√2 units.
The perimeter of the sign is 2(2√2) + 4 + 2(2)
= 8 + 4√2 = 13.657 units
Question 4.
Graph the directed line segment ST with endpoints S(- 3, – 2) and T(4, 5). Then find the coordinates of point P along the directed line segment ST so that the ratio of SP to PT is 3 to 4.
Answer:
Graph the directed line segment ST with endpoints S(- 3, – 2) and T(4, 5).
4 – (-3) = 4 + 3 = 7
The point P along the directed line segment ST so that the ratio of SP to PT is 3 to 4.
P = -3 + 3 = 0
P = (0, 1)
Question 5.
The graph shows quadrilateral WXYZ and quadrilateral ABCD.
a. Write a composition of transformations that maps quadrilateral WXYZ to
quadrilateral ABCD.
Answer:
It can be seen that ABCD and WXYZ are symmetrical about the line y = -x
It can be concluded that WXYZ can be mapped on to ABCD by reflection in the line y = -x
b. Are the quadrilaterals congruent? Explain your reasoning.
Answer:
Reflection is a transformation that does not change the size of an image with respect to its preimage.
So it can be said that the quadrilateral ABCD and WXYZ are congruent.
Question 6.
Which equation represents the line passing through the point (- 6, 3) that is parallel to
the line y = – \(\frac{1}{3}\)x – 5?
(A) y = 3x + 21
(B) y = –\(\frac{1}{3}\)x – 5
(C) y = 3x – 15
() y = –\(\frac{1}{3}\)x + 1
Answer:
y = mx + c
y = –\(\frac{1}{3}\)x – 5
Slope = –\(\frac{1}{3}\)
point (-6, 3)
y = –\(\frac{1}{3}\)x + n
3 = –\(\frac{1}{3}\) (-6) + n
n = 1
y = –\(\frac{1}{3}\)x + 1
Thus the correct answer is option D.
Question 7.
Which scale factor(s) would create a dilation of \(\overline{A B}\) that is shorter than \(\overline{A B}\)? Select all that apply.

Answer:
In order to create a dilation of AB that is shorter than AB, the dilation factor must greater than 0 but less than 1
Therefore the possible values of the dilation factor here are 1/3, 1/2 and 3/4
Question 8.
List one possible set of coordinates of the vertices of quadrilateral ABCD for each description.
a. A reflection in the y-axis maps quadrilateral ABCD onto itself.
Answer:
If the preimage and image of the figure are same after the reflection in the y-axis, then this implies that the line of symmetry of the quadrilateral is the y-axis.
Thus the coordinates can be A(-1, 2), B(1, 2), C(1, -2) and D(-1, -2)
b. A reflection in the x-axis maps quadrilateral ABCD onto itself
Answer:
If the preimage and image of a figure are same after reflection in the x-axis then this implies that the line of symmetry of the quadrilateral is the x-axis.
The coordinates can be A(-1, 2), B(1, 2), C(1, -2) and D(-1, -2)
c. A rotation of 90° about the origin maps quadrilateral ABCD onto itself.
Answer:
If the preimage and image of a figure are same after reflection 90° about the origin then this implies that the quadrilateral has a rotational symmetry.
The coordinates can be A(-1, 1), B(1, 1), C(1, -1) and D(-1, -1)
d. A rotation of 180° about the origin maps quadrilateral ABCD onto itself.
Answer:
If the preimage and image of a figure are same after reflection 180° about the origin then this implies that the quadrilateral has a rotational symmetry.
The coordinates can be A(-1, 2), B(1, 2), C(1, -2) and D(-1, -2)
