Hello students!!! Are you looking for the Big Ideas Math Grade 8 Answer Key on various sites? If yes, then finally you are on the right page. The students of 8th Grade can get the easy and detailed solutions for Big Ideas Math Answers 8th Std Chapter 2 transformations. Download Big Ideas Math Answers Grade 8 Chapter 2 Transformations pdf for free and start your preparation to secure the highest marks in the exams.
Big Ideas Math Book 8th Grade Answer Key Chapter 2 Transformations
Our main aim is to provide the step by step explanations for all the students of Grade 8. The solutions of Middle School Big Ideas Math Grade 8 key Chapter 2 Transformations are prepared by the math experts. Just tap the links given below and practice the problems and improve your skills.
Performance
Lesson: 1 Translations
Lesson: 2 Reflections
Lesson: 3 Rotations
Lesson: 4 Congruent Figures
Lesson: 5 Dilations
Lesson: 6 Similar Figures
Lesson: 7 Perimeters and Areas of Similar Figures
- Lesson 2.7 Perimeters and Areas of Similar Figures
- Perimeters and Areas of Similar Figures Homework & Practice 2.7
Chapter 2: Transformations
- Transformations Connecting Concepts
- Transformations Practice Test
- Transformations Cumulative Practice
Transformations STEAM Video/Performance
STEAM Video
Shadow Puppets
Some puppets are controlled using strings or wires. How else can a puppet be controlled?

Watch the STEAM Video “Shadow Puppets.” Then answer the following questions.
Question 1.
Tory and Robert are using a light source to display puppets on a screen. Tory wants to show the pig jumping from the floor to the window. Should she use a translation, reflection, rotation, or dilation? Explain.

Answer:
In the situation given, if we translate first, we move the pre-image closer to the center of dilation than if we translate second. That will result in a different image.
Question 2.
How can Tory show the pig getting smaller as it jumps out the window?
Performance Task
Master Puppeteer
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given the coordinates of a kite being used bya puppeteer.

You will be asked to identify transformations for given movements of the kite. When might a puppeteer want to use a reflection?
Transformations Getting Ready for Chapter 2
Getting Ready for Chapter 2
Chapter Exploration

Question 1.
Work with a partner. Form each triangle on a geoboard.
- Which of the triangles are congruent to the triangle at the right?
- Measure the sides of each triangle with a ruler. Record your results in a table.
- Write a conclusion about the side lengths of triangles that are congruent.

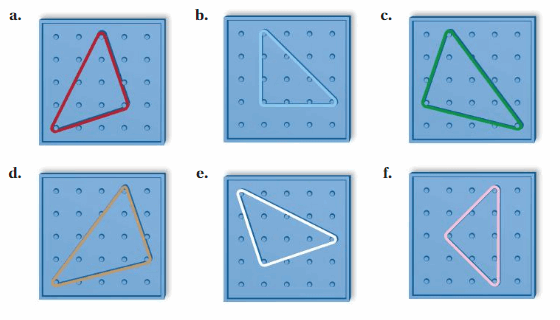
Answer: option d
When two triangles are congruent they will have exactly the same three sides and exactly the same three angles. The equal sides and angles may not be in the same position
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what the terms might mean and record your thoughts.
Lesson 2.1 Translations
EXPLORATION 1
Work with a partner.
a. For each figure below, draw the figurein a coordinate plane. Then copy the figureonto a piece of transparent paper and slide the copy to a new location in the coordinate plane. Describe the location of the copy compared to the location of the original.
- point
- triangle
- line segment
- rectangle
- line

b. When you slide figures, what do you notice about sides, angles, and parallel lines?
c. Describe the location of each point below compared to the point A(x, y).
B(x + 1, y + 2)
C(x – 3, y + 4)
D(x – 2, y + 3)
E(x + 4, y – 1)
d. You copy a point with coordinates (x, y) and slide it horizontally a units and vertically b units. What are the coordinates of the copy?
2.1 Lesson
Try It
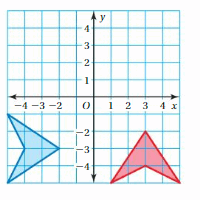
Tell whether the blue figure is a translation of the red figure.
Question 1.
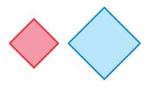
Answer:
Here in the given figure, we can see that the shape of both red and blue figures is the same but the size is different. The red figure slide to form a blue figure but it is not the same size. So blue figure is not the translation of red figure.
Question 2.
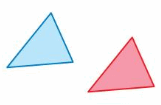
Answer:
Here in the given figure, we can see that the shape of both red and blue figures is the same and also the size is the same. The red figure slide to form exactly blue figure. So blue figure is the translation of red figure.
Try It
Question 3.
WHAT IF?
The red triangle is translated 4 units left and 2 units up. What are the coordinates of the image?
Answer:
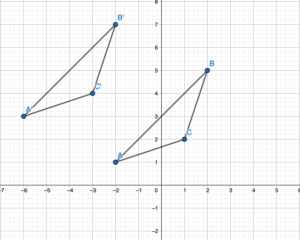
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if shift is Right and Vertical Up and the value of a and b will be negative if shift is left and vertical Down.
Given: A(-2,1) B(2,5), C(1,2) and a = -4, b = 2
A'(-2+a, -2+b) = A'(-2-4, 1+2) = A'(-6,3)
B'(2+a, 5+b) = B'(2-4, 5+2) = B'(-2,7)
A'(1+a, 2+b) = C'(1-4, 2+2) = C'(-3,4)
Hence the coordinate of image are A'(-6,3), B'(-2,7), C'(-3,4).
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
IDENTIFYING A TRANSLATION
Tell whether the blue figure is a translation of the red figure.
Question 4.
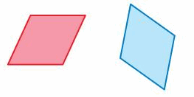
Answer:
Here in the given figure, we can see that the shape of both red and blue figures is the same but the size is different. The red figure slide to form a blue figure but it is not the same size. So blue figure is not the translation of red figure.
Question 5.
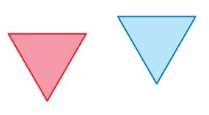
Answer:
Here in the given figure, we can see that the shape of both red and blue figures is the same, and also the size is the same. The red figure slide to form the exactly blue figure. So blue figure is the translation of red figure.
Question 6.
The vertices of a triangle are A(2, 2), B (0, 2), and C (3, 0). Translate the triangle 1 unit left and 2 units up. What are the coordinates of the image?
Answer:
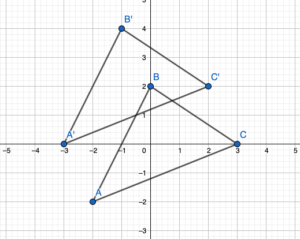
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if shift is Right and Vertical Up and the value of a and b will be negative if shift is left and vertical Down.
Given: A(2,2) B(0,2), C(3,0) and a = -1, b = 2
A'(2+a, 2+b) = A'(2-1, 2+2) = A'(1,4)
B'(0+a, 2+b) = B'(0-1, 2+2) = B'(-1,4)
A'(3+a, 0+b) = C'(3-1, 0+2) = C'(2,2)
Hence the coordinate of image are A'(1,4), B'(-1,4), C'(2,2).
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
A neighborhood planner uses a coordinate plane to design a new neighborhood. The coordinates A(1, -1), B(1, -2), and C (2, -1) represent House A, House B, and House C. The planner decides to place a playground centered at the origin, and moves the houses to make space. House A is now located at A'(3, -4). What are the new coordinates of House B and House C when each house is moved using the same translation? Justify your answer.
Answer:
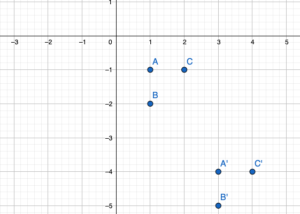
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if shift is Right and Vertical Up and the value of a and b will be negative if shift is left and vertical Down.
Given: A(1,-1) B(1,-2), C(2,1) and A'(3,-4)
A'(1+a, -1+b) = A'(3,-4) So, a = 2, b = -3
New coordinates of the houses are
B'(1+a, -2+b) = B'(1+2, -2-3) = B'(3,-5)
C'(2+a, -1+b) = C'(2+2, -1-3) = C'(4,-4)
Hence the coordinate of image are B'(3,-5),C'(4,-4)
Question 8.
The locations of a quarterback and a wide receiver on a football field are represented in a coordinate plane. The quarterback throws the football to the point (6, -2). Use a translation to describe a path the wide receiver can take to catch the pass.
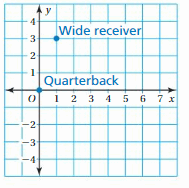
Answer:
Coordinate of Receiver: (1,3) and football point:(-6,-2)
Horizontal shift: a = x2-x1 = 6 – 1 = 5
Verrical shift: b = y2 – y1 = -2 – 3 = -5
Hence the path which receiver will take 5 unit right and 5 unit down.
Translations Homework & Practice 2.1
Review & Refresh
Solve the equation for y.
Question 1.
6x + y = 12
Answer:
Given
6x + y = 12
Subtract 6x from both sides
y = 12 – 6x
Now arranging the terms
y = -6x + 12
y = 6 (-x + 2)
Thus y = 6(-x + 2)
Question 2.
9 = x + 3y
Answer:
Given,
9 = x + 3y
3y = 9 – x
Dividing by 3 on both sides
y = (9 – x)/3
y = \(\frac{9}{3}\) – \(\frac{x}{3}\)
Now arranging the terms
y = – \(\frac{x}{3}\) + 3
Thus y = – \(\frac{x}{3}\) + 3
Question 3.
\(\frac{1}{3}\)x + 2y = 8
Answer:
Given,
\(\frac{1}{3}\)x + 2y = 8
Subtracting x/3 from both sides
2y = 8 – \(\frac{x}{3}\)
Now arranging the terms
2y = – \(\frac{x}{3}\) + 8
y = – \(\frac{x}{6}\) + 4
Question 4.
You put $550 in an account that earns 4.4% simple interest per year. How much interest do you earn in 6 months?
A. $1.21
B. $12.10
C. $121.00
D. $145.20
Answer: $12.10
Explanation:
Given:
You put $550 in an account that earns 4.4% simple interest per year.
Principal amount: P = $550
Rate of Interest: r = 4.4%
Time: t = 6 months = 0.5 year
We know that formula for Simple Interest is SI = prt/100
SI = (550 × 4.4 × 0.5)/100
SI = 1210/100
SI = 12.10
Hence the simple interest is $12.10
Thus the correct answer is option B.
Concepts, Skills, & Problem Solving
DESCRIBING RELATIONSHIPS
For each figure, describe the location of the blue figurerelative to the location of the red figure. (See Exploration 1, p. 43.)
Question 5.
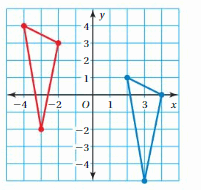
Answer: The path which the receiver will take is 6 units right and 3 units down.
Explanation:
Coordinate of Point A: (-3,2) and Point A’: (3,-5)
Horizontal shift: a = x2 – x1 = 3 – (-3) = 3 + 3 = 6
Vertical shift: b = y2 – y1 = -5 – (-2) = -5 + 2 = -3
Hence, The path which the receiver will take is 6 units right and 3 units down.
Question 6.
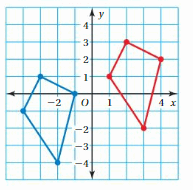
Answer: The path which receive will take is 5 units left and 2 units down.
Explanation:
Coordinate of point A: (3,-2) and point A’: (-2,-4)
Horizontal shift: a = x2 – x1 = -2 – (3) = -2 – 3 = -5
Vertical shift: b = y2 – y1 = -4 – (-2) = -4 + 2 = -2
Hence, The path which receive will take is 5 unit left and 2 unit down.
IDENTIFYING A TRANSLATION
Tell whether the blue figure is a translation of the red figure.
Question 7.
Answer:
Blue figure is the translation of red figure.
Explanation:
Here in the given figure, we can see that the shape of both blue and red figures are the same, and also the size of both the figure are the same. Also, the orientation of the blue figure is the same as the red figure. This means that the red figure sides to form the blue figure. So, the blue figure slides to form the red figure.
Question 8.
Answer:
Blue figure is not the translation of the red figure.
Explanation:
Here in the given figure, we can see that the shape of both blue and red figures are the same, and also the size of both the figure are the same. But the orientation of the blue figure is different from the red figure. This means that the blue figure is not the translation of the red figure.
Question 9.
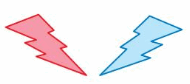
Answer:
Blue figure is not the translation of the red figure.
Explanation:
Here in the given figure, we can see that the shape of both blue and red figures are the same, and also the size of both the figure are the same. But the orientation of the blue figure is different from the red figure. This means that the blue figure is not the translation of the red figure. The blue figure is the mirror image of the red figure.
Question 10.
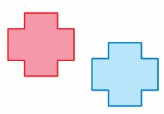
Answer:
Blue figure is the translation of red-figure.
Here in the given figure, we can see that the shape of both blue and red-figure are the same, and also the size of both the figure are the same. Also, the orientation of the blue figure is the same as the red figure. This means that the red figure slides to form the blue figure. so the figure slides to form the red figure.
Question 11.
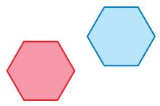
Answer:
Blue figure is the translation of red-figure.
Explanation:
Here in the given figure, we can see that the shape of both blue and red figures are the same, and also the size of both the figures are the same. Also, the orientation of the both figure is the same as the red figure. This means that the red figure slides to form the blue figure. So blue figure slides to form the red figure.
Question 12.
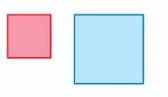
Answer: Blue figure is not the translation of the red-figure.
Explanation:
Here in the given figure we can see that the shape of both blue and red figure are same and the size of both the figure are not same. The red figure are smaller as compared to the blue figure. This means that blue figure is not the translation of red figure.
TRANSLATE A FIGURE
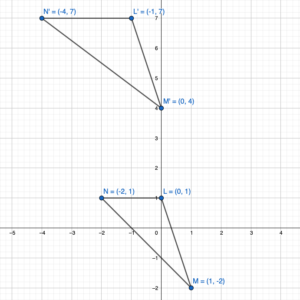
The vertices of a triangle are L(0, 1), M(1, -2), and N(-2, 1). Draw the figure and its image after the translation.
Question 13.
1 unit left and 6 units up
Answer:
explanation:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to the x-coordinate and ‘b’ is added to the y-coordinates of the vertices.
A(x,y) – A'(x+a, y+b)
The value ‘a’ and ‘b’ will be positive if the shift is Right and Vertical up and the value of ‘a’ and ‘b’ will be negative if the shift is left and vertical down.
Given:L(0,1),M(1,-2),N(-2,1)anda=-1,b=6
L'(0+a,1+b)=l'(0-1,1+6)=L'(-1,7)
M'(1+a,-2+b)=M'(1-1,1+6)=M'(0,4)
N'(-2+a,1+b)=N'(-3-1,1+6)=N'(-4,7)
Hence,the coordinate of image are L'(-1,7),M'(0,4),N'(-4,7)
Question 14.
5 units right
Answer:
We know that to translate a figure ‘a’ units horizontal and ‘b’ units vertically in the coordinate plane, ‘a’ is added to X-coordinate and ‘b’ is added to Y-coordinate of the vertices.
a(x,y),=A'(x+a,y+b)
the value ‘a’ and ‘b’ will be positive if the shift is right and vertical up and the value of ‘a’ and ‘b’ will be negative if shift is left and vertical down.
Given:L(0,1),M(1,-2),N(-2,1)and a=5,b=0
L(0+a,1+b)=L'(0+5,1+0)=L'(5,1)
M'(1+a,-2=b)=M'(1+5,-2+0)=M'(6,-2)
N'(-2+a,1+b)=N'(-2+5,1+0)=N'(3,1)
Hence the coordinate of image are L'(5,1),M'(6,-2),N'(3,1).
Question 15.
(x + 2, y + 3)
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
the value of a and b will be positive if the shift is Right and vertical Up and the value of a and b will be negative if the shift is left and vertical down.
Given: L(0,1), M(1,-2), N(-2,1) and (x+2,y+3)
So the value of: a = 2 and b = 3
L'(o + a, 1 + b) = L'(0 + 2,1 + 3) = L'(2,4)
M'(1+a, -2 + b) = M'(1 + 2, -2 + 3) = M'(3, 1)
N'(-2 + a, 1 + b) = N'(-2 + 2, 1 + 3) = N'(0, 4)
Hence the coordinate of the image is L'(2,4), M'(3,1), N'(0,4)
Question 16.
(x – 3, y – 4)
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
the value of a and b will be positive if the shift is Right and vertical Up and the value of a and b will be negative if the shift is left and vertical down.
Given: L(0,1), M(1,-2), N(-2,1) and (x-3, y-4)
So the value of a = -3 and b = -4
L'(0 + a, 1 + b) = L'(0-3,1-4) = L'(-3,-3)
M'(1 + a, -2 + b) = M'(1 – 3, -2-4) = M'(-2,-6)
N'(-2 + a, 1 + b) = N'(-2 – 3, 1 – 4) = N'(-5, -3)
Hence the coordinate of the image are L'(-3,-3), M'(-2,-6), N'(-5, -3)
Question 17.
YOU BE THE TEACHER
Your friend translates point A 2 units down and 1 unit right. Is your friend correct? Explain your reasoning.
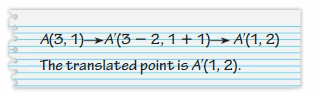
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to the y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
the value of a and b will be positive if the shift is Right and vertical Up and the value of a and b will be negative if the shift is left and vertical down.
Given points,
A(3, 1) and a = 1, b = -2
A'(3+a, 1+b) = A'(3+1, 1-2) = A'(4, -1)
So, the point A’ translated by my friend is wrong. He has reversed the x and y coordinate for translation.
Hence the correct translate point is A'(4,-1)
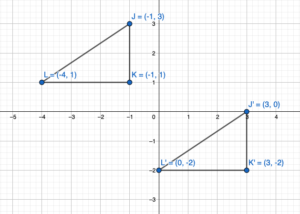
Question 18.
TRANSLATING A FIGURE
Translate the triangle 4 units right and 3 units down. What are the coordinates of the image?
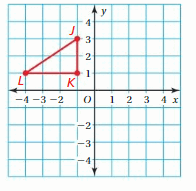
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
the value of a and b will be positive if the shift is Right and vertical Up and the value of a and b will be negative if the shift is left and vertical down.
Given points from graph: J(-1,3), K(-1,1), L(-4,1)
and a = 4, b = -3
J'(-1 + a, 3 + b) = J'(-1+4,3-3) = J'(3,0)
K'(-1 + a, 1 + b) = K'(-1 + 4, 1 – 3) = K'(3,-2)
L'(-4 + a, 1 + b) = L'(-4 + 4, 1 – 3) = L'(0,-2)
Hence the coordinate of image is J'(3,0), K'(3,-2), L'(0,-2)
Question 19.
TRANSLATING A FIGURE
Translate the figure 2 units left and 4 units down. What are the coordinates of the image?
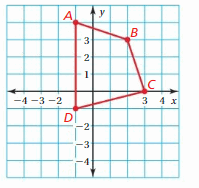
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
the value of a and b will be positive if the shift is Right and vertical Up and the value of a and b will be negative if the shift is left and vertical down.
Given: A(-1,4), B(2,3), C(3,0), D(-1,-1)
and a = -2, b = -4
A'(-1+a, 4+b) = A'(-1-2, 4-4) = A'(-3,0)
B'(2+a, 3+b) = B'(2-2, 3-4) = B'(0,-1)
C'(3+a, 0+b) = C'(3-2, 0-4) = C'(1,-4)
D'(-1+a, -1+b) = D'(-1-2, -1-4) = D'(-3,-5)
The coordinate of image are A'(-3,0), B'(0,-1), C'(1,-4), D'(-3,-5)
DESCRIBING A TRANSLATION
Describe the translation of the point to its image.
Question 20.
(3, 2) → (1,0)
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
the value of a and b will be positive if the shift is Right and vertical Up and the value of a and b will be negative if the shift is left and vertical down.
Coordinate of the point A:(3,-2) and the image point A’:(1,0)
Horizontal shift: a = x2 – x1 = 1 – 3 = -2
Vertical shift: b = y2 – y1 = 0 – (-2) = 0 + 2 = 2
Hence the translation path will be 2 units left and 2 units up.
Question 21.
(-8, -4) → (-3, 5)
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
the value of a and b will be positive if the shift is Right and vertical Up and the value of a and b will be negative if the shift is left and vertical down.
Coordinate of the point A:(-8,-4) and the image point A’:(-3,5)
Horizontal shift: a = x2 – x1 = -3 – (-8) = 5
Vertical shift: b = y2 – y1 = 5 – (-4) = 9
Hence the translation path will be 5 units left and 9 units up.
Question 22.
REASONING
You can click and drag an icon on a computer’s desktop. Is this an example of a translation? Explain.
Answer:
Yes, the dragging of an icon on a computer’s desktop is an example of translation.
Because when dragging an icon on desktop the icon directly slides and is stored in its new position. While dragging the icon there is no change in shape and size of the icon, thus fulfilling the criteria of translation.
Question 23.
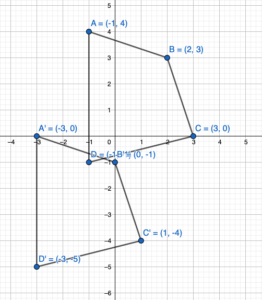
MODELING REAL LIFE
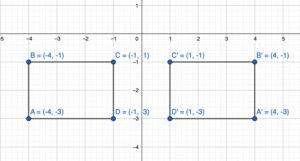
The proposed location for a new oil platform is represented in a coordinate plane by a rectangle with vertices A(1, 3), B(1, 4), C(4, 4), and D(4, -3). An inspector recommends moving the oil platform 4 units right and 2 units down. Find the coordinates of the image. Then draw the original figureand the image in the coordinate plane.
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to the y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
the value of a and b will be positive if the shift is Right and vertical Up and the value of a and b will be negative if the shift is left and vertical down.
Given: A(1,-3), B(1,4), C(4,4), D(4,-3) and a = 4, b = -2
A'(1+a, -3+b) = A'(1+4, -3-2) = A'(5,-5)
B'(1+a, 4+b) = B'(1+4, 4-2) = B'(5,2)
C'(4+a, 4+b) = C'(4+4, 4-2) = C'(8,2)
D'(4+a, -3+b) = D'(4+4, -3-2) = D'(8,-5)
Hence the coordinate of image are A'(5,-5), B'(5,2), C'(8,2), D'(8,-5)
Question 24.
PROBLEM SOLVING
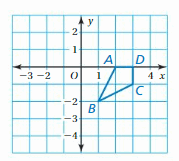
A school of fish translates from point F to point D.
a. Describe the translation of the school of fish.
b. Can the fishing boat make the same translation? Explain.
c. Describe a translation the fishing boat could make to get to point D.
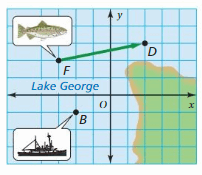
Answer:
a. Coordinate of the point F: (-3,2) and the point D: (2,3)
Horizontal shift: a = x2 – x1 = 2 – (-3) = 2 + 5 = 7
Vertical shift: b = y2 – y1 = 3 – 2 = 1
Hence the path of translation is 5 unit Right and 1 unit Up.
b. No, the fishing boat (point B) cannot make the same translation as by fish (point F). Because in path between from point B to point D the is an island which will interrupt the translation of fishing boat.
c. Coordinate of the point B:(-2,-1) and the point D: (2,3)
Horizontal shift: a = x2 – x1 = 2 – (-2) = 2 + 2 = 4
Verical shift: b = y2 – y1 = 3 -(-1) = 3 + 1 = 4
Hence the path of translation is 4 unit Right and 4 unit Up.
Question 25.
REASONING
The vertices of a triangle are A(0, -3), B(2, -1), and C(3, -3). You translate the triangle 5 units right and 2 units down. Then you translate the image 3 units left and 8 units down. Is the original triangle identical to the final image? Explain your reasoning.
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
the value of a and b will be positive if the shift is Right and vertical Up and the value of a and b will be negative if the shift is left and vertical down.
Given: A(0,-3), B(2,-1), C(3,-3) and a1 = 5, b1 = -2
A'(0+a, -3+b) = A'(0+5, -3-2) = A'(5,-5)
B'(2+a, -1+b) = B'(2+5, -1-2) = B'(7,-3)
C'(3+a, -3+b) = C'(3+5,-3-2) = C'(8,-5)
Hence the coordinate of the first image are A'(5,-5), B'(7,-3), C'(8,-5)
Given: A'(5,-5), B'(7,-3), C'(8,-5) and a2 = -3, b2 = -8
A”(5+a, -5+b) = A”(5-3, -5-8) = A”(2,-13)
B”(7+a, -3+b) = B”(7-3, -3-8) = B”(4,-11)
C”(8+a, -5+b) = C”(8-3,-5-8) = C”(5,-13)
Hence the coordinate of the first image are A”(2,-13), B”(4,-11), C”(5,-13)
a = a1+a2 = 5 – 3 = 2, and b = b1 + b2 = -2 – 8 = -10
A'(0+a, -3+b) = A'(0+2, -3-10) = A'(2,-13)
B'(2+a, -1+b) = B'(2+2, -1-10) = B'(4,-11)
C'(3+a, -3+b) = C'(3+2,-3-10) = C'(5,-13)
Hence the original triangle is identical to the final image. This is because we can use both the translation by finding the resultant translation.
For final translation we can use:(x+2, y-10)
Question 26.
DIG DEEPER!
In chess, a knight can move only in an L-shaped pattern:
- two vertical squares, then one horizontal square;
- two horizontal squares, then one vertical square;
- one vertical square, then two horizontal squares; or
- one horizontal square, then two vertical squares.
Write a series of translations to move the knight from g8 to g5.

Answer:
The series of translation to move knight from g8 to g5
1. Move 1 units Right to h8 and then 2 units Down to h6
2. Move 2 units Left to f6 and then 1 unit Up to f7
3. Move 2 units Down to f5 and then 1 unit Right to g5
Lesson 2.2 Reflections
Reflecting Figures
Work with a partner.
a. For each figure below, draw the figure in the coordinate plane. Then copy the axes and the figure onto a piece of transparent paper. Flip the transparent paper and align the origin and the axes with the coordinate plane. For each pair of figures, describe the line of symmetry.
- point
- triangle
- line segment
- rectangle
- line
b. When you reflect figures, what do you notice about sides, angles, and parallel lines?
c. Describe the relationship between each point below and the point A(4, 7) in terms of reflections.
d. A point with coordinates (x, y) is reflected in the x-axis. What are the coordinates of the image?
e. Repeat part(d) when the point is reflected in the y-axis
2.2 Lesson
Try It
Tell whether the blue figure is a reflection of the red figure.
Question 1.
Answer: Blue figure is not the reflection of the red figure
Explanation:
By seeing the above figure we can say that the blue figure is not the mirror image of the red figure. Thus Blue figure is not the reflection of the red figure.
Question 2.
Answer: Blue figure is the reflection of the red figure
Explanation:
By seeing the above figure we can say that the blue figure is the mirror image of the red figure. If the red figure is flipped it would form the shape of the blue figure. Thus Blue figure is the reflection of the red figure
Try It
Question 3.
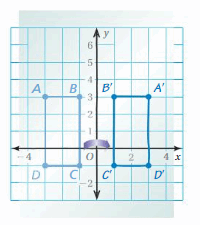
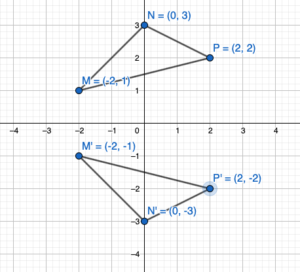
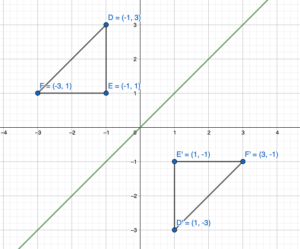
The vertices of a rectangle are A(-4, -3), B(-4, -1), C(-1, -1), and D(-1, -3). Draw the figure and its reflection in (a) the x-axis and (b) the y-axis.
Answer:
Given,
The vertices of a rectangle are A(-4, -3), B(-4, -1), C(-1, -1), and D(-1, -3).
Reflection about the x-axis:
A(x,y) = A'(x,-y)
A(-4, -3) = A'(-4,3)
B(-4, -1) = B'(-4,1)
C(-1, -1) = C'(-1,1)
D(-1, -3) = D'(-1,3)
Reflection through x-axis:
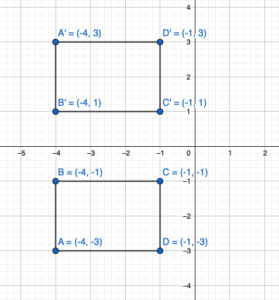
Reflection through y-axis:
A(x,y) = A'(-x,y)
A(-4, -3) = A'(4,-3)
B(-4, -1) = B'(4,-1)
C(-1, -1) = C'(1,-1)
D(-1, -3) = D'(1,-3)
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
REFLECTING A FIGURE
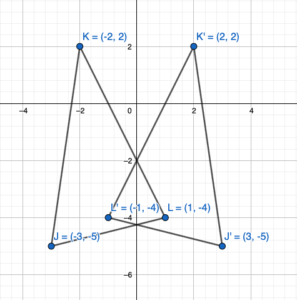
The vertices of a triangle are J(-3, -5), K(-2, 2), and L(1, -4). Draw the figure and its reflection in
(a) the x-axis and
(b) the y-axis.
Answer:
When a point is reflected about the x-axis then the y coordinate becomes the opposite.
A(x,y) = A'(x,-y)
The vertices of a triangle are J(-3, -5), K(-2, 2), and L(1, -4).
Reflection about the x-axis:
J(-3, -5) = J'(-3,5)
K(-2, 2) = K'(-2,-2)
L(1, -4) = L'(1,4)
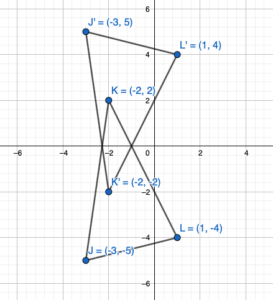
when a point is reflected about the y-axis then the x coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Reflection about the y-axis:
J(-3, -5) = J'(3,-5)
K(-2, 2) = K'(2,2)
L(1, -4) = L'(-1,-4)
Question 5.
WHICH ONE DOESN’T BELONG?
Which transformation does not belong with the other three? Explain your reasoning.

Answer: 3rd figure is different from other figures. Because all the other three pictures are reflections of each other except the third one. The third picture is pointed in the same direction but all the other three figures are in opposite direction.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
You design a logo using the figure shown at the left. You want both the x-axis and the y-axis to be lines of reflection. Describe how to use reflections to complete the design. Then draw the logo in the coordinate plane.
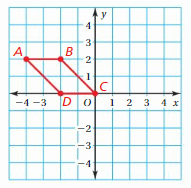
Answer:
When a point is reflected about the x-axis then the y coordinate becomes the opposite.
A(x,y) = A'(x,-y)
A(-4,2), B(-2,2), C(0,0), D(-2,0)
Reflection about the x-axis:
A(-4,2) = A'(-4,-2)
B(-2,2) = B'(-2,-2)
C(0,0) = C'(0,0)
D(-2,0) = D'(-2,0)
when a point is reflected about the y-axis then the x coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Reflection about the y-axis:
A(-4,2) = A”(4,2)
B(-2,2) = B”(2,2)
C(0,0) = C”(0,0)
D(-2,0) = D”(2,0)
Now to complete the Logo again we have to take a reflection of the image figure about the y-axis. In this way, the logo will be symmetric about both axis.
A”(4,2) = A”‘(4,-2)
B”(2,2) = B”‘(2,-2)
C”(0,0) = C”‘(0,0)
D”(2,0) = D”‘(-2,0)
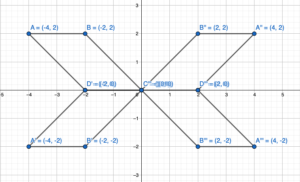
Question 7.
DIG DEEPER!
You hit the golf ball along the path shown, so that its final location is a reflection in the y-axis of its starting location.
a. Does the golf ball land in the hole? Explain.
b. Your friend tries the shot from the same starting location. He bounces the ball of the wall at the point (-0.5, 7) so that its path is a reflection. Does the golf ball land in the hole?
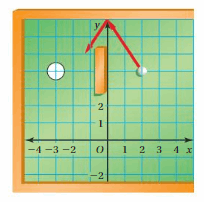
Answer:
a. Coordinates of the location of golf ball = (2,4)
Coordinates of location of hole = (-3,4)
Location of ball after reflection through y-axis = (2,4) = (-2,4)
But the location of the hole is (-3,4)
So the ball will not go into a hole and it will miss the hole by 1 unit.
Hence the ball will not go into the hole.
b. Yes, when the ball bounces at the point (-0.5,7) then it will land in the hole.
Reflections Homework & Practice 2.2
Review & Refresh
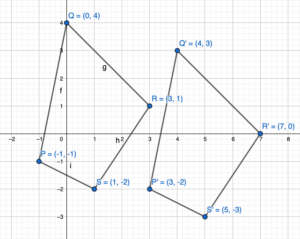
The vertices of a quadrilateral are P(-1, -1), Q(0, 4), R(3, 1), and S(1, -2). Draw the figure and its image after the translation.
Question 1.
7 units down
Answer:
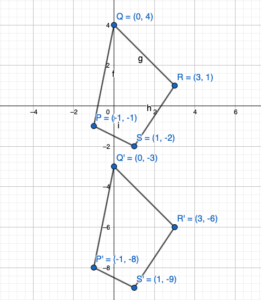
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinates of the vertices.
A(x,y) = A'(x+a,y+b)
the value ‘a’ and ‘b’ will be positive if shift is right and vertical up and the value of ‘a’ and ‘b’ will be negative if shift is left and vertical down.
Given,
P(-1,-1)
Q(0,4)
R(3,1)
S(1,-2) and a = 0, b = -7
P'(-1+a,-1+b) = P'(-1+0,-1-7) = P'(-1,-8)
Q'(0+a,4+b) = Q'(0+4,4-7) = Q'(4,-3)
R'(3+a, 1+b) = R'(3+0,1-7) = R'(3,-6)
S'(1+a,-2+b) = S'(1+0,-2-7) = S'(1,-9)
Thus the coordinate of the image is P'(-1,-8), Q'(4,-3), R'(3,-6), and S'(1,-9)
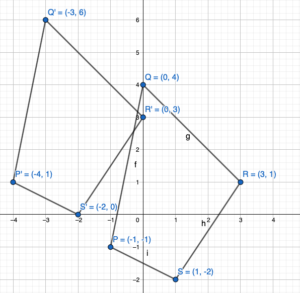
Question 2.
3 units left and 2 units up
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinates of the vertices.
A(x,y) = A'(x+a,y+b)
the value ‘a’ and ‘b’ will be positive if shift is right and vertical up and the value of ‘a’ and ‘b’ will be negative if shift is left and vertical down.
Given,
P(-1,-1)
Q(0,4)
R(3,1)
S(1,-2) and a = -3, b = 2
P'(-1+a,-1+b) = P'(-1-3,-1+2) = P'(-4,1)
Q'(0+a,4+b) = Q'(0-3,4+2) = Q'(-3,6)
R'(3+a, 1+b) = R'(3-2,1+2) = R'(0,3)
S'(1+a,-2+b) = S'(1-3,-2+2) = S'(-2,0)
Thus the coordinate of the image are P'(-4,1), Q'(-3,6), R'(0,3) and S'(-2,0)
Question 3.
(x + 4, y – 1)
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinates of the vertices.
A(x,y) = A'(x+a,y+b)
the value ‘a’ and ‘b’ will be positive if shift is right and vertical up and the value of ‘a’ and ‘b’ will be negative if shift is left and vertical down.
Given,
P(-1,-1)
Q(0,4)
R(3,1)
S(1,-2) and a = 4, b = -1
P'(-1+a,-1+b) = P'(-1+4,-1-1) = P'(3,-2)
Q'(0+a,4+b) = Q'(0+4,4-1) = Q'(4,3)
R'(3+a, 1+b) = R'(3+4,1-1) = R'(7,0)
S'(1+a,-2+b) = S'(1+4,-2-1) = S'(5,-3)
Thus the coordinate of the image are P'(3,-2), Q'(4,3), R'(7,0) and S'(5,-3)
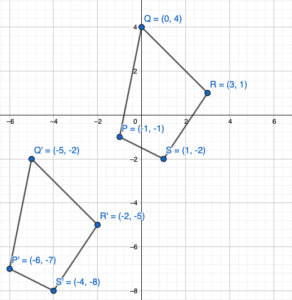
Question 4.
(x – 5, y – 6)
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinates of the vertices.
A(x,y) = A'(x+a,y+b)
the value ‘a’ and ‘b’ will be positive if shift is right and vertical up and the value of ‘a’ and ‘b’ will be negative if shift is left and vertical down.
Given,
P(-1,-1)
Q(0,4)
R(3,1)
S(1,-2) and a = -5, b = -6
P'(-1+a,-1+b) = P'(-1-5,-1-6) = P'(-6,-7)
Q'(0+a,4+b) = Q'(0-5,4-6) = Q'(-5,-2)
R'(3+a, 1+b) = R'(3-5,1-6) = R'(-2,-5)
S'(1+a,-2+b) = S'(1-5,-2-6) = S'(-4,-8)
Thus the coordinate of the image are P'(-6,-7), Q'(-5,-2), R'(-2,-5) and S'(-4,-8)
Tell whether the angles are complementary, supplementary or neither.
Question 5.
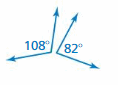
Answer:
108° + 82° = 190°
Thus the angle is neither supplementary nor complementary.
Question 6.
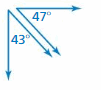
Answer: Complementary
Explanation:
43° + 47° = 90°
Two angles are called complementary when their measures add to 90 degrees.
Question 7.
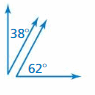
Answer:
38° + 62° = 100°
Hence the given angle is neither supplementary nor complementary.
Question 8.
36 is 75% of what number?
A. 27
B. 48
C. 54
D. 63
Answer: B. 48
Explanation:
Let x be the unknown value.
75% of x = 36
75% × x = 36
75/100 × x = 36
3/4x × x = 36
3x = 36 × 4
3x = 144
x = 144/3
x = 48
Thus the correct answer is option B.
Concepts, Skills, &Problem Solving
DESCRIBING RELATIONSHIPS
Describe the relationship between the given point and the point A(5, 3) in terms of reflections. (See Exploration 1, p. 49.)
Answer:
We know that when a point is reflected about x-axis then y-coordinate becomes the opposite.
P(x,y) = P'(x,-y)
We know that when a point is reflected about y-axis then x-coordinate becomes opposite.
P(x,y) = P'(-x,y)
Given: A(5,3), B(5,-3)
Hence the point A is reflected about the x-axis to get point B.
IDENTIFYING A REFLECTION
Tell whether the blue figure is a reflection of the red figure.
Question 12.
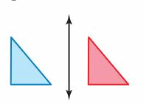
Answer: No
Explanation:
The blue figure is not the mirror image of the red figure. If the red figure were flipped then the right of the blue and red figure should be facing each other. So, the blue figure is not a reflection of red figure.
Question 13.
Answer: Yes
Explanation:
The blue figure is the mirror image of the red figure. If the red figure were flipped it will result in the blue figure. So, the blue figure is a reflection of red figure.
Question 14.
Answer: Yes
Explanation:
The blue figure is the mirror image of the red figure. If the red figure were flipped it will result in the blue figure. So, the blue figure is a reflection of red figure.
Question 15.
Answer: No
Explanation:
The blue figure is not the mirror image of the red figure. If the red figure were flipped then the right of the blue and red figure should be facing each other. So, the blue figure is not a reflection of red figure.
Question 16.
Answer: Yes
Explanation:
The blue figure is the mirror image of the red figure. If the red figure were flipped it will result in the blue figure. So, the blue figure is a reflection of red figure.
Question 17.
Answer: No
Explanation:
The blue figure is not the mirror image of the red figure. If the red figure were flipped then the right of the blue and red figure should be facing each other. So, the blue figure is not a reflection of red figure.
REFLECTING FIGURES
Draw the figure and its reflection in the x-axis. Identify the coordinates of the image.
Question 18.
A(3, 2), B(4, 4), C(1, 3)
Answer:
We know that when a point is reflected about the x-axis then y-coordinate becomes the opposite.
A(x,y) = A'(x,-y)
We know that when a point is reflected about the y-axis then the x-coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given,
A(3, 2), B(4, 4), C(1, 3)
Reflection about the x-axis:
A(3, 2) = A'(3,-2)
B(4, 4) = B'(4,-4)
C(1, 3) = C'(1,-3)
Thus the coordinate of the image are A'(3,-2), B'(4,-4), C'(1,-3)
Question 19.
M(-2, 1), N(0, 3), P(2, 2)
Answer:
We know that when a point is reflected about the x-axis then y-coordinate becomes the opposite.
A(x,y) = A'(x,-y)
We know that when a point is reflected about the y-axis then the x-coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given,
M(-2, 1), N(0, 3), P(2, 2)
Reflection about the x-axis:
M(-2, 1) = M'(-2,-1)
N(0, 3) = N'(0,-3)
P(2, 2) = P'(2,-2)
Thus the coordinate of the image are M'(-2,-1), N'(0,-3), P'(2,-2)
Question 20.
H(2, -2), J(4, -1), K(6, -3), L(5, -4)
Answer:
We know that when a point is reflected about the x-axis then y-coordinate becomes the opposite.
A(x,y) = A'(x,-y)
We know that when a point is reflected about the y-axis then the x-coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given,
H(2, -2), J(4, -1), K(6, -3), L(5, -4)
Reflection about the x-axis:
H(2, -2) = H'(-2,-1)
J(4, -1) = J'(4,1)
K(6, -3) = K'(6,3)
L(5, -4) = L'(5,4)
Thus the coordinate of the image are H'(-2,-1), J'(4,1), K'(6,3) and L'(5,4)

Question 21.
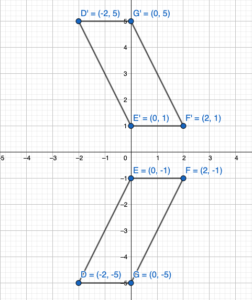
D(-2, -5), E(0, -1), F(2, -1), G(0, -5)
Answer:
We know that when a point is reflected about the x-axis then y-coordinate becomes the opposite.
A(x,y) = A'(x,-y)
We know that when a point is reflected about the y-axis then the x-coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given,
D(-2, -5), E(0, -1), F(2, -1), G(0, -5)
Reflection about the x-axis:
D(-2, -5) = D'(-2,5)
E(0, -1) = E'(0,1)
F(2, -1) = F'(2,1)
G(0, -5) = G'(0,5)
Thus the coordinate of the image are D'(-2,5), E'(0,1), F'(2,1), G'(0,5)
REFLECTING FIGURES
Draw the figure and its reflection in the y-axis. Identify the coordinates of the image.
Question 22.
Q(-4, 2), R(-2, 4), S(-1, 1)
Answer:
We know that when a point is reflected about the y-axis then the x-coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given,
Q(-4, 2), R(-2, 4), S(-1, 1)
Reflection about the x-axis:
Q(-4, 2) = Q'(4,2)
R(-2, 4) = R'(2,4)
S(-1, 1)= S'(1,1)
Thus the coordinate of the image is Q'(4,2), R'(2,4), S'(1,1)
Question 23.
T(4, -2), U(4, 2), V(6, -2)
Answer:
We know that when a point is reflected about the y-axis then the x-coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given,
T(4, -2), U(4, 2), V(6, -2)
Reflection about the y-axis
T(4,-2) = T'(-4,-2)
Y(4,2) = U'(-4,2)
V(6,-2) = V'(-6,-2)
Thus the coordinates of the figure are T'(-4,-2), U'(-4,2), V'(-6,-2)
Question 24.
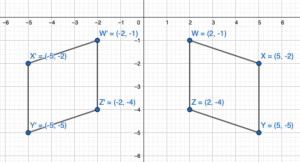
W(2, -1), X(5, -2), Y(5, -5), Z(2, -4)
Answer:
We know that when a point is reflected about the y-axis then the x-coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given,
W(2, -1), X(5, -2), Y(5, -5), Z(2, -4)
Reflection about the y-axis:
W(2,-1) = W'(-2,-1)
X(5,-2) = X'(-5,-2)
Y(5,-5) = Y'(-5,-5)
Z(2,-4) = Z'(-2,-4)
Thus the coordinates of the figure are W'(-2,-1), X'(-5,-2), Y'(-5,-5), Z'(-2,-4)
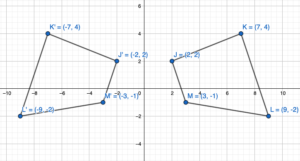
Question 25.
J(2, 2), K(7, 4), L(9, -2), M(3, -1)
Answer:
We know that when a point is reflected about the y-axis then the x-coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given,
J(2, 2), K(7, 4), L(9, -2), M(3, -1)
Reflection about the y-axis
J(2, 2) = J(-2,2)
K(7, 4) = K'(-7,4)
L(9, -2) = L'(-9,-2)
M(3, -1) = M'(-3,-1)
Thus the coordinates of the figure are J(-2,2), K'(-7,4), L'(-9,-2), M'(-3,-1)
Question 26.
REASONING
Which letters look the same when reflected in the line?

Answer:
The letters which will look the same after being reflected through horizontal line are
B, C, D, E, H, I, K, O, X
STRUCTURE
The coordinates of a point and its image after a reflection are given. Identify the line of reflection.
Question 27.
(2, -2) → (2, 2)
Answer:
When a point is reflected about the x-axis then the y coordinate becomes the opposite.
A(x,y) = A'(x,-y)
when a point is reflected about the y-axis then the x coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given A(2, -2) → A'(2, 2)
Here we can see that x-coordinate of both A & A’ is the same but the y-coordinate of A’ is just the opposite of A. This means that A’ is the reflection of A about the x-axis.
Hence the point A is reflected about the x-axis to get point A’.
Question 28.
(-4, 1) → (4, 1)
Answer:
When a point is reflected about the x-axis then the y coordinate becomes the opposite.
A(x,y) = A'(x,-y)
when a point is reflected about the y-axis then the x coordinate becomes the opposite.
A(x,y) = A'(-x,y)
Given A(-4, 1) → A'(4, 1)
Here we can see that y-coordinate of both A & A’ is the same but the x-coordinate of A’ is just the opposite of A. This means that A’ is the reflection of A about y-axis.
Hence the point A is reflected about the y-axis to get point A’.
Question 29.
(-2, -5) → (4, -5)
Answer:
Given,
A(-2, -5) → A'(4, -5)
We observe that y-coordinate of both A and A’ is same but the x-coordinate of A’ is not opposite of A. This means that A’ is the reflection of A about a line x = a.
a = (x2+x1)/2 = (4-2)/2 = 2/2 = 1
Hence the point (-2,-5) is reflected about the line x = 1 to get point (4,-5)
Question 30.
(-3, -4) → (-3, 0)
Answer:
Given,
B(-3, -4) → B'(-3, 0)
We observe that x-coordinate of both B and B’ is the same but the y-coordinate of B’ is not the opposite of B. This means that A’ is the reflection of A about a line x = a.
b = (y2+y1)/2 = (0-4)/2 = -4/2 = -2
Hence the point (-3,-4) is reflected about the line y = -2 to get point (-3,0)
TRANSFORMING FIGURES
Find the coordinates of the figure after the transformations.
Question 31.
Translate the triangle 1 unit right and 5 units down. Then reflect the image in the y-axis.
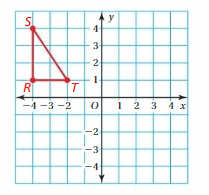
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if the shift is Right and Vertical Up and the value of a and b will be negative if the shift is left and vertical Down.
Given:
R(-4,1)
S(-4,4)
T(-2,1)
a = 1 and b = -5
R(-4,1) = R'(-4+a, 1+b) = R'(-4+1, 1-5) = R'(-3, -4)
S(-4,4) = S'(-4+a, 4+b) = S'(-4+1, 4-5) = S'(-3, -1)
T(-2,1) = T'(-2+a, 1+b) = T'(-2+1, 1-5) = T'(-1, -4)
Thus the coordinates of the image are R'(-3, -4), S'(-3, -1), T'(-1, -4)
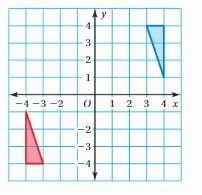
Question 32.
Reflect the trapezoid in the x-axis. Then translate the image 2 units left and 3 units up.
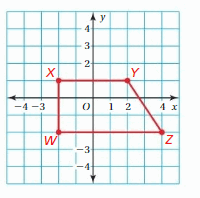
Answer:
When a point is reflected about the x-axis then the y coordinate becomes the opposite.
A(x,y) = A'(x,-y)
Given, W(-2,-2), X(-2,1), Y(2,1), and Z(4,-2)
Now reflection about the x-axis:
W(-2,-2) = W'(-2,2)
X(-2,1) = X'(-2,-1)
Y(2,1) = Y'(2,-1)
Z(4,-2) = Z'(4,2)
Thus the coordinates of the image: W'(-2,2), X'(-2,-1), Y'(2,-1), Z'(4,2)
Now translating the above image point:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to the y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if the shift is Right and Vertical Up and the value of a and b will be negative if the shift is left and vertical Down.
Given:
W(-2,-2), X(-2,1), Y(2,1), and Z(4,-2)
a = -2 and b = 3
W(-2,2) = W”(-2+a, 2+b) = W”(-2-2, 2+3) = W”(-4, 5)
X(-2,-1) = X”(-2+a, -1+b) = X”(-2-2, -1+3) = X”(-4, 2)
Y(2,-1) = Y”(2+a, -1+b) = Y”(2-2, -1+3) = Y”(0, 2)
Z(4,2) = Z”(4+a, 2+b) = Z”(4-2, 2+3) = Z”(2, 5)
Thus the coordinates of the image: W”(-4, 5), X”(-4, 2), Y”(0, 2), Z”(2, 5)
Question 33.
REASONING
In Exercises 31 and 32, is the original figure identical to the final image? Explain.
Answer: Yes, in exercises 31 and 32 the original figure is identical to the final image. Because the type of transformation used is reflection and translation. The shape and size of the image figure do not change when there is reflection or translation. The only position of the image changes in both cases when compared to the position of the original figure.
Question 34.
CRITICAL THINKING
Hold a mirror to the left side of the photo of the vehicle.
a. What word do you see in the mirror?
Answer: The word which we will see in the mirror will be AMBULANCE. Because the word is written in mirror image form on the vehicle.
b. Why do you think it is written that way on the front of the vehicle?

Answer: Ambulance
Explanation:
It is written in that way because the ambulance will be behind any vehicle then the word “AMBULANCE” will correctly appear in the Rear-view mirror of the front vehicle.
Question 35.
DIG DEEPER!
Reflect the triangle in the line y = x. How are the x- and y-coordinates of the image related to the x- and y-coordinates of the original triangle?
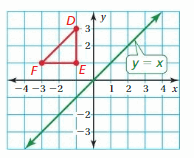
Answer:
When a point is reflected about the line y = x then both x and y-coordinate become opposite.
A(x, y) = A'(-x, -y)
Given,
D(-1,-3)
E(-1,1)
F(-3,1)
Reflection about the line y = x
D(-1,-3) = D'(1,-3)
E(-1,1) = E'(1,-1)
F(-3,1) = F'(3,-1)
Hence the coordinates of the image: D'(1,-3), E'(1,-1), F'(3,-1)
Lesson 2.3 Rotations
EXPLORATION 1
Work with a partner.
a. For each figurebelow, draw the figure in the coordinate plane. Then copy the axes and the figure onto a piece of transparent paper. Turn the transparent paper and align the origin and the axes with the coordinate plane. For each pair of figures, describe the angle of rotation.

- point
- triangle
- line segment
- rectangle
b. When you rotate figures, what do you notice about sides, angles, and parallel lines?
c. Describe the relationship between each point below and the point A(3, 6) in terms of rotations.
d. What are the coordinates of a point P(x, y) after a rotation 90° counterclockwise about the origin? 180°? 270°?
2.3 Lesson
Try It
Tell whether the blue figure is a rotation of the red figure about the origin. If so, give the angle and direction of rotation.
Question 1.
Answer: Yes blue figure is the rotation of red figure about the origin.
Explanation:
When we rotate the red figure 180 degrees clockwise or anti-clockwise about the origin we will get the same figure as the blue figure.
Question 2.
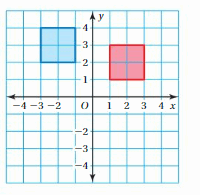
Answer: Blue figure is not the rotation of the red figure.
Explanation:
When the red figure is rotated about the origin in any direction the distance of the center point of both the red figure and the blue figure will be the same from the origin point (0,0). The distance between the center of the object and the center of rotation always remains the same.
Thus Blue figure is not the rotation of the red figure.
Try It
The vertices of a figure are given. Rotate the figure as described. Find the coordinates of the image.
Question 3.
J(-4, -4), K(-4, 2), L(-1, 0), M(-2, -3); 180° about the origin
Answer:
When a point is rotated 180 degrees about the origin then both x and y-coordinates become opposite.
A(x, y) = A'(-x, -y)
Given, J(-4, -4), K(-4, 2), L(-1, 0), M(-2, -3)
Rotation about the origin
J(-4, -4) = J'(4,4)
K(-4, 2) = K'(4,-2)
L(-1, 0) = L'(1,0)
M(-2, -3) = M'(2,3)
Hence the coordinate of the image are J'(4,4), K'(4,-2), L'(1,0), M'(2,3)
Question 4.
P(-3, 2), Q(6, 1), R(-1, -5); 90° counterclockwise about the origin
Answer:
When a point is rotated 90 degrees about the origin then both x and y-coordinates become opposite.
A(x, y) = A'(-y, x)
Given,
P(-3, 2), Q(6, 1), R(-1, -5)
Rotation about the origin
P(-3, 2) = P'(-2,-3)
Q(6, 1) = Q'(-1,6)
R(-1, -5) = R'(5,-1)
Hence the coordinate of the image is P'(-2,-3), Q'(-1,6), R'(5,-1)
Question 5.
A(5, 3), B(4, -1), C(1, -1); 90° clockwise about the origin
Answer:
When a point is rotated 270 degrees counterclockwise about the origin then both x and y-coordinates gets interchanged and the x-coordinate becomes the opposite.
A(x, y) = A'(y, -x)
Given,
A(5, 3), B(4, -1), C(1, -1)
Rotation about the origin
A(5, 3) = A'(3,-5)
B(4, -1) = B'(-1,-4)
C(1, -1) = C'(-1,-1)
Hence the coordinate of the image are A'(3,-5), B'(-1,-4), C'(-1,-1)
Try It
Question 6.
The vertices of a triangle are P(-1, 2), Q(-1, 0), and R(2, 0). Rotate the triangle 180° about the origin, and then reflect it in the x-axis. What are the coordinates of the image?
Answer:
When a point is rotated 180 degrees about the origin then both x and y-coordinates become opposite.
A(x, y) = A'(-x, -y)
Given,
P(-1, 2), Q(-1, 0), and R(2, 0)
Rotation about the origin
P(-1, 2) = P'(1,-2)
Q(-1, 0) = Q'(1,0)
R(2, 0) = R'(-2,0)
Hence the coordinate of the image is P'(1,-2), Q'(1,0), R'(-2,0)
Now reflecting above image point about x-axis:
When a point is reflected about the x-axis then the y-coordinate becomes opposite.
A(x, y) = A'(x, -y)
Given,
P'(1,-2), Q'(1,0), R'(-2,0)
Rotation about the origin
P'(1,-2) = P”(1,2)
Q'(1,0) = Q”(1,0)
R'(-2,0) = R”(-2,0)
Hence the coordinate of the image are P'(1,2), Q'(1,0), R'(-2,0)
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
IDENTIFYING A ROTATION
Tell whether the blue figure is a rotation of the red figure about point P. If so, give the angle and direction of rotation.
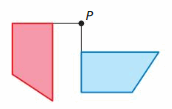
Answer:
Yes, the blue figure is the rotation of the red figure about the origin.
Explanation:
Because when we will rotate the red figure 90 degrees anti-clockwise about the origin we will get the same figure as the blue figure.
By this, we can say that the blue figure is the result of the rotation of red figure by 90 degrees in the clock or anti-clockwise direction.
Question 8.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
The statement which different from all other 3 statement is:
What are the coordinates of the image after a 270 degrees clockwise rotation about the origin?
Now coordinate of both the image are:
The rotation of an object 90 degrees clockwise is equal to the rotation of 270 degrees counterclockwise.
we know that when a point is rotated 270 degrees counterclockwise about origin then both coordinate gets interchanges and x-coordinate becomes opposite.
A(x, y) = A'(y, -x)
Given,
A(2, 4)
B(4, 4)
C(4, 1)
Rotating 90 degrees clockwise about the origin
A(2,4) = A'(4,-2)
B(4, 4) = B'(4,-4)
C(4, 1) = C'(1,-4)
Hence the coordinate of the image are: A'(4,-2), B'(4,-4), C'(1,-4)
Image of statement which different from all 3 statement
The rotation of an object 270 degrees clockwise is equal to the rotation of 90 degrees counterclockwise.
we know that when a point is rotated 90 degrees counterclockwise about origin then both coordinate gets interchanges and x-coordinate becomes opposite
P(x, y) = P'(-y, x)
Given,
A(2, 4)
B(4, 4)
C(4, 1)
Rotating 90 degrees clockwise about the origin
A(2, 4) = A'(-4, 2)
B(4, 4) = B'(-4, 4)
C(4, 1) = C'(-1, 4)
Hence the coordinate of the image are: A'(4,-2), B'(-4,4), C'(-1,4)
Third statement “what are the coordinates of the image after a 270 degrees clockwise rotation about origin?” is different.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
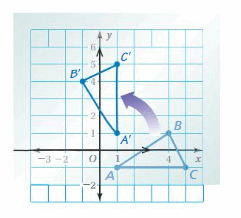
You move the red game piece to the indicated location using a rotation about the origin, followed by a translation. What are the coordinates of the vertices of the game piece after the rotation? Justify your answer.
Answer:
To move the red game piece in the indicated location the game piee should be rotated 90 degrees in clockwise direction. The rotation of red game piece 90 degrees clockwise is same as the rotation of 270 degrees counterclockwise.
we know that when a point is rotated 270 degrees counterclockwise about origin then both coordinate gets interchanges and x-coordinate becomes opposite.
A(x,y) = A'(y, -x)
Conner point of red game piece:
A(0,-1), B(0,0), C(1,0), D(1,1), E(-2,1), F(-2,0), G(-1,0), H(-1,-1)
Rotating 90 degrees clockwise about the origin:
A(0,-1) = A'(-1,0)
B(0,0) = B'(0,0)
C(1,0) = C'(0,-1)
D(1,1) = D'(1,-1)
E(-2,1) = E'(1,2)
F(-2,0) = F'(0,2)
G(-1,0) = G'(0,1)
H(-1,-1) = H'(-1,1)
Hence the coordinate of corner of red game piece are A'(-1,0), B'(0,0), C'(0,-1), D'(1,-1), E'(1,2), F'(0,2), G'(0,1), H'(-1,1)
Question 10.
DIG DEEPER!
Skytypingis a technique that airplanes use to write messages in the sky. The coordinate plane shows a message typed in the sky over a city, where the positive y-axis represents north. What does the message say? How can you transform the message so that it is read from north to south?
Answer: HELLO
Explanation:
The message above on the coordinate plane can be transformed from north to south by rotating the image 90 degrees anticlockwise.
Rotations Homework & Practice 2.3
Review & Refresh
Tell whether the blue figure is a reflection of the red figure.
Question 1.
Answer: Yes, the blue figure is the reflection of red figure.
Explanation:
Because the blue figure is the exact mirror image of the red figure. If the red figure will be flipped it will result in the blue figure. So, the blue figure is the reflection of red figure.
Question 2.
Answer: No, the blue figure is not the reflection of red figure.
Explanation:
Because the blue figure is not the mirror image of the red figure. If the red figure will be flipped it will not result in the blue figure. So blue figure is not reflection of red figure.
Find the circumference of the object. Use 3.14 or \(\frac{22}{7}\) for π.
Question 3.
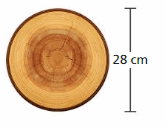
Answer:
Given diameter of disk D = 28 cm
Circumference of the circular disk is π × D
C = π × 28
C = 22/7 × 28
C = 22 × 4
C = 88 cm
Thus the circumference is 88 cm.
Question 4.

Answer:
Given the diameter of disk D = 11.4 in
Circumference of the circular disk is π × D
C = π × 11.4
C = 22/7 × 11.4
C = 3.14 × 11.4
C = 35.796 in
Thus the circumference is 35.796 in
Question 5.
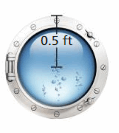
Answer:
Given diameter of disk r = 0.5 ft
Circumference of the circular disk is 2π × r
C = 2π × 0.5
C = 6.28 × 0.5
C = 3.14 ft
Thus the circumference is 3.14 ft
Concepts, Skills, &Problem Solving
DESCRIBING RELATIONSHIPS
Describe the relationship between the given point and the point (2, 7) in terms of rotations. (See Exploration 1, p. 55.)
Question 6.
B(7, -2)
Answer:
Given,
A(7, 2) = B(7, -2)
Here we can see that after rotation x and y coordinate are interchanged and the y-coordinate is opposite. And we know that when a point is rotated 270 degrees counterclockwise about origin then both coordinates get interchanged and the x-coordinate becomes opposite.
P(x, y) = P'(y, -x)
Hence the above rotation is 270 degrees counterclockwise about the origin.
Question 7.
C(-7, 2)
Answer:
Given,
A(7, 2) = C(-7, 2)
Here we can see that after rotation x and y coordinate are interchanged and the y-coordinate is opposite. And we know that when a point is rotated 270 degrees counterclockwise about origin then both coordinate gets interchanged and x-coordinate becomes opposite.
P(x, y) = P'(-y, x)
Hence the above rotation is 90 degrees counterclockwise about the origin.
Question 8.
D(-2, -7)
Answer:
Given,
A(2, 7) = C(-2, -7)
Here we can see that after rotation x and y coordinate are interchanged and the y-coordinate is opposite. And we know that when a point is rotated 270 degrees counterclockwise about origin then both coordinate gets interchanged and x-coordinate becomes opposite.
P(x, y) = P'(-x, -y)
Hence the above rotation is 180 degrees counterclockwise about the origin.
IDENTIFYING A ROTATION
Tell whether the blue figure is a rotation of the red figure about the origin. If so, give the angle and direction of rotation.
Question 9.
Answer: No the blue figure is not the rotation of the red figure.
Explanation:
Because if the blue triangle were the result of the rotation of the red triangle then the hypotenuse of the blue triangle should have been parallel to the x-axis. so, it is not the case of rotation.
Question 10.
Answer: Yes, the blue figure is the result of the rotation of the red figure.
Explanation:
Because if the red figure is rotated 90 degrees in a counterclockwise direction it will result in a blue figure.
Question 11.
Answer: Yes, the blue figure is the result of the rotation of the red figure.
Explanation:
If the red figure is rotated 180 degrees in counterclockwise or clockwise direction it will result in blue figure.
Question 12.
Answer: Yes, the blue figure is the result of the rotation of the red figure.
Explanation:
If the red figure is rotated 90 degrees in a clockwise direction it will result in blue figure.
ROTATING A FIGURE
The vertices of a figure are given. Rotate the figure as described. Find the coordinates of the image.
Question 13.
A(2, -2), B(4, -1), C(4, -3), D(2, -4)
90° counterclockwise about the origin
Answer:
We know that when a point is rotated 90 degrees counterclockwise about the origin then both coordinates gets interchanged and y-coordinate becomes opposite.
P(x, y) = P'(-y, x)
Given,
A(2, -2), B(4, -1), C(4, -3), D(2, -4)
Rotating 90 degrees counterclockwise about the origin
A(2, -2) = A'(2,2)
B(4, -1) = B'(1,4)
C(4, -3) = C'(3,4)
D(2, -4) = D'(4,2)
Hence the coordinates of the image are A'(2,2), B'(1,4), C'(3,4), D'(4,2)
Question 14.
F(1, 2), G(3, 5), H(3, 2) 180° about the origin
Answer:
We know that when a point is rotated 180 degrees counterclockwise or clockwise direction about the origin then both coordinates gets interchanged and y-coordinate becomes opposite.
P(x, y) = P'(-x, -y)
Given,
F(1, 2), G(3, 5), H(3, 2)
Rotating 180 degrees about the origin
F(1, 2) = F'(-1,-2)
G(3, 5) = G'(-3,-5)
H(3, 2) = H'(-3,-2)
Hence the coordinates of the image are F'(-1,-2), G'(-3,-5), H'(-3,-2)
Question 15.
J(-4, 1), K(-2, 1), L(-4, -3)
90° clockwise about the origin
Answer:
The rotation of an object 90 degrees clockwise is equal to the rotation of 270 degrees counterclockwise.
We know that when a point is rotated 270 degrees counterclockwise about the origin then both coordinates gets interchanged and y-coordinate becomes opposite.
P(x, y) = P'(y, -x)
Given,
J(-4, 1), K(-2, 1), L(-4, -3)
Rotating 90 degrees clockwise about the origin
J(-4, 1) = J'(1,4)
K(-2, 1) = K'(1,2)
L(-4, -3) = L'(-3,4)
Hence the coordinates of the image are J'(1,4), K'(1,2), L'(-3,4)
Question 16.
P(-3, 4), Q(-1, 4), R(-2, 1), S(-4, 1)
270° clockwise about the origin
Answer:
The rotation of an object 270 degrees clockwise is equal to the rotation of 90 degrees counterclockwise.
We know that when a point is rotated 90 degrees counterclockwise about the origin then both coordinates gets interchanged and y-coordinate becomes opposite.
P(x, y) = P'(-y, x)
Given,
P(-3, 4), Q(-1, 4), R(-2, 1), S(-4, 1)
Rotating 90 degrees clockwise about the origin
P(-3, 4) = P'(-4,-3)
Q(-1, 4) = Q'(-4,-1)
R(-2, 1) = R'(-1,-2)
S(-4, 1) = S'(-1,-4)
Hence the coordinates of the image are P'(-4,-3), Q'(-4,-1), R'(-1,-2), S'(-1,-4)
Question 17.
W(-6, -2), X(-2, -2), Y(-2, -6), Z(-5, -6)
270° counterclockwise about the origin
Answer:
We know that when a point is rotated 270 degrees counterclockwise about the origin then both coordinates gets interchanged and y-coordinate becomes opposite.
P(x, y) = P'(y, -x)
Given,
W(-6, -2), X(-2, -2), Y(-2, -6), Z(-5, -6)
Rotating 90 degrees clockwise about the origin
W(-6, -2) = W'(-2,6)
X(-2, -2) = X'(-2,2)
Y(-2, -6) = Y'(-6,2)
Z(-5, -6) = Z'(-6,5)
Hence the coordinates of the image are W'(-2,6), X'(-2,2), Y'(-6,2), Z'(-6,5)
Question 18.
A(1, -1), B(5, -6), C(1, -6)
90° counterclockwise about the origin
Answer:
We know that when a point is rotated 90 degrees counterclockwise about the origin then both coordinates gets interchanged and y-coordinate becomes opposite.
P(x, y) = P'(-y, x)
Given,
A(1, -1), B(5, -6), C(1, -6)
Rotating 90 degrees clockwise about the origin
A(1, -1) = A'(1,1)
B(5, -6) = B'(6,5)
C(1, -6) = C'(6,1)
Hence the coordinates of the image are A'(1,1), B'(6,5), C'(6,1)
Question 19.
YOU BE THE TEACHER
The vertices of a triangle are A(4, 4), B(1, -2), and C(-3, 0). Your friend finds the coordinates of the image after a rotation 90° clockwise about the origin. Is your friend correct? Explain your reasoning.

Answer:
We know that when a point is rotated 270 degrees counterclockwise about the origin then both coordinates gets interchanged and y-coordinate becomes opposite.
P(x, y) = P'(y, -x)
Given,
A(4, 4), B(1, -2), and C(-3, 0).
Rotating 90 degrees clockwise about the origin
A(4, 4) = A'(4,-4)
B(1, -2) = B'(-2,-1)
C(-3,0) = C'(0,3)
Hence the coordinates of the image are A'(4,-4), B'(-2,-1), C'(0,3)
By this I can say that my friend is not correct.
Question 20.
PROBLEM SOLVING
A game show contestant spins the prize wheel shown. The arrow remains in a fixed position while the wheel rotates. The wheel stops spinning, resulting in an image that is a rotation 270° clockwise about the center of the wheel. What is the result?
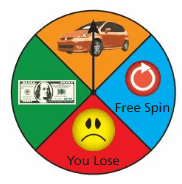
Answer: Free spin
Explanation:
The arrow is located at 90 degrees in the counterclockwise direction of free spin. So when the wheel is rotated 270 degrees in a clockwise direction the arrow will be on the free spin column.
PATTERN
A figure has rotational symmetry if a rotation of 180° or less produces an image that fits exactly on the original figure. Determine whether the figure has rotational symmetry. Explain your reasoning.
Question 21.
Answer: Yes the given figure has rotational symmetry.
Explanation:
The given figure in the problem is rotated 120 degrees in any direction clockwise or counterclockwise then it will produce the same identical image. Since 120 degrees is less than 180 degrees so it will have rotational symmetry.
Question 22.

Answer: No the given figure does not have rotational symmetry.
Explanation:
The given figure in the problem will produce the same identical image only when it is rotated 360 degrees. Since 360 degrees is greater than 180 degrees so it will not have rotational symmetry.
Question 23.

Answer: Yes the given figure has rotational symmetry.
Explanation:
The given figure in the problem will produce the same identical image only when it is rotated 180 degrees. Since the maximum angle for rotational symmetry is 180 degrees so it will have rotational symmetry.
USING MORE THAN ONE TRANSFORMATION
The vertices of a figure are given. Find the coordinates of the image after the transformations given.
Question 24.
R(-7, -5), S(-1, -2), T(-1, -5)
Rotate 90° counterclockwise about the origin. Then translate 3 units left and 8 units up.
Answer:
We know that when a point is rotated 90 degrees counterclockwise about origin then both coordinates gets interchanges and y-coordinate becomes opposite.
P(x,y) = P'(-y,x)
Given, R(-7, -5), S(-1, -2), T(-1, -5)
Rotating 90 degrees counterclockwise about the origin
R(-7,-5) = R'(5,-7)
S(-1, -2) = S'(2,-1)
T(-1, -5) = T'(5,-1)
The coordinate of the image are R'(5,-7), S'(2,-1), T'(5,-1)
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if shift is Right and Vertical Up and the value of a and b will be negative if shift is left and vertical Down.
Given, R'(5,-7), S'(2,-1), T'(5,-1) and a = -3, b = 8
R'(5+a, -7+b) = R”(5-3, -7+8) = R”(2,1)
S'(2+a, -1+b) = R”(2-3, -1+8) = S”(-1,7)
R'(5+a, -1+b) = R”(5-3, -1+8) = T”(2,7)
The coordinate of the image are R”(2,1), S”(-1,7), T”(2,7)
Question 25.
J(-4, 4), K(-3, 4), L(-1, 1), M(-4, 1) Reflect in the x-axis, and then rotate 180° about the origin.
Answer:
We know that when a point is reflected about x-axis then y-coordinate becomes opposite.
A(x, y) = A'(x, -y)
Given J(-4, 4), K(-3, 4), L(-1, 1), M(-4, 1)
Reflection about the x-axis:
J(-4, 4) = J'(-4,-4)
K(-3, 4) = K'(-3,-4)
L(-1, 1) = L'(-1,-1)
M(-4, 1) = M'(-4,-1)
The coordinate of the image are J'(-4,-4), K'(-3,-4), L'(-1,-1), M'(-4,-1)
Now rotating the above image 180 degrees about the origin.
We know that when a point is reflected about x-axis then y-coordinate becomes opposite.
A(x, y) = A'(-x, -y)
J'(-4,-4), K'(-3,-4), L'(-1,-1), M'(-4,-1)
Rotating 180 degrees about the origin:
J'(-4,-4) = J”(4,4)
K'(-3,-4) = K”(3,4)
L'(-1,-1) = L”(1,1)
M'(-4,-1) = M”(4,1)
The coordinate of the image are J”(4,4), K”(3,4), L”(1,1), M”(4,1)
CRITICAL THINKING
Describe two different sequences of transformations in which the blue figure is the image of the red figure.
Question 26.
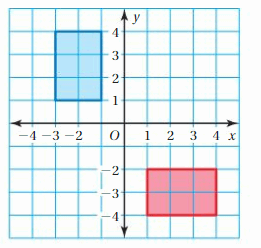
Answer:
Two different ways of translating a red figure in to blue figure:
1. First rotate the red figure 90 degrees in the counterclockwise direction and then translate that image 5 units towards the left to get the blue figure.
2. First rotate the red figure 90 degrees in a clockwise direction and then translate that image 1 unit towards the Right and 5 units Up to get the blue figure.
Question 27.
Answer:
Two different ways of translating a red figure in to blue figure:
1. First rotate the red figure 90 degrees in the counterclockwise direction and then translate that image 1 unit towards the left and 1 Down to get the blue figure.
2. First rotate the image in the x-axis and then translate that image 4 units towards the left and 2 units Up to get the blue figure.
Question 28.
REASONING
A trapezoid has vertices A(-6, -2), B(-3, -2), C(-1, -4), and D(-6, -4).
a. Rotate the trapezoid 180° about the origin. What are the coordinates of the image?
Answer:
A(x, y) = A'(-x, -y)
Given,
A(-6, -2), B(-3, -2), C(-1, -4), and D(-6, -4).
Rotating 180 degrees about the origin:
A(-6, -2) = A'(6,2)
B(-3, -2) = B'(3,2)
C(-1, -4) = C'(1,4)
D(-6, -4) = D'(6,4)
The coordinates of the image of trapezoid vertices are A'(6,2), B'(3,2), C'(1,4), D'(6,4)
b. Describe a way to obtain the same image without using rotations.
Answer:
In the above question, we can see that the coordinates of all the vertices of the trapezoid are negative and all the coordinates of the image vertices are positive. So there is another way to get the vertices of the image.
First, reflect the trapezoid in the x-axis and then in the y-axis or first reflect the trapezoid in the y-axis and then in the x-axis.
ROTATING A FIGURE
The vertices of a figure are given. Rotate the figure as described. Find the coordinates of the image.
Question 29.
D(2, 1), E(2, -2), F(-1, 4)
90° counterclockwise about vertex D
Answer:
P(x, y) = P'(-(y – b) + a, (x -a) + b)
Given,
D(2, 1), E(2, -2), F(-1, 4)
(a, b) = (2, 1)
Rotation about the point D(2,1)
D(2, 1) = D'(2,1)
E(2, -2) = E'(-(-2-1) + 2, (2 – 2) + 1) = E'(5, 1)
F(-1, 4) = F'(-(4 – 1) + 2, (-1 – 2) + 1) = F'(-1, -2)
Hence the coordinate of the image: D'(2,1), E'(5, 1), F'(-1, -2)
Question 30.
L(-4, -3), M(-1, -1), N(2, -2)
180° about vertex M
Answer:
When a point is rotated 180 degrees counterclockwise about a given point (a, b) then its both x and y coordinate becomes opposite and ‘b’ and ‘a’ are subtracted from x and y coordinate respectively.
P(x, y) = P'(-(x – a) + b, -(y – b) + a)
Given,
L(-4, -3), M(-1, -1), N(2, -2)
Rotation about the point M(-1, -1):
L(-4, -3) = L'(-(-4 + 1) – 1, -(-3 + 1) – 1) = L'(2, 1)
M(-1, -1) = M'(-1, -1)
N(2, -2) = N'(-(2 + 1) – 1, -(-2 + 1) – 1) = N'(-4, 0)
Hence the coordinate of the image are L'(2, 1), M'(-1, -1), N'(-4, 0)
Question 31.
W(-5, 0), X(-1, 4), Y(3, -1), Z(0, -4)
270° counterclockwise about vertex W
Answer:
When a point is rotated 270 degrees counterclockwise about a given point (a, b) then its both x and y coordinate becomes opposite and ‘b’ and ‘a’ are subtracted from x and y coordinate respectively.
P(x, y) = P'(-(x – a) + b, -(y – b) + a)
Given,
W(-5, 0), X(-1, 4), Y(3, -1), Z(0, -4)
Rotation about the point W(-5, 0):
W(-5, 0) = W'(-5, 0)
X(-1, 4) = X'((4 – 0) – 5, -(-1 + 5) + 0) = X'(-1, -4)
Y(3, -1) = Y'((-1 – 0) – 5, -(3 + 5) + 0) = Y'(-6, -8)
Z(0, -4) = Z'((-4 – 0) – 5, -(0 + 5) + 0) = Z'(-9, -5)
Hence the coordinate of the image are W'(-5, 0), X'(-1, -4), Y'(-6, -8), Z'(-9, -5)
Question 32.
D(-3, -4), E(-5, 2), F(1, -1), G(3, -7)
270° clockwise about vertex E.
Answer:
When a point is rotated 90 degrees counterclockwise about a given point (a, b) then its both x and y coordinate becomes opposite and ‘b’ and ‘a’ are subtracted from x and y coordinate respectively.
P(x, y) = P'(-(x – a) + b, -(y – b) + a)
Given,
D(-3, -4), E(-5, 2), F(1, -1), G(3, -7)
Rotation about the point E(-5, 2):
D(-3, -4) = D'(-(-4 – 2) – 5, -(-3 + 5) + 2) = D'(1, 4)
E(-5, 2) = E'(-5, 2)
F(1, -1) = F'(-(-1 – 2) – 5, (1 + 5) + 2) = F'(-2, 8)
G(3, -7) = G'(-(-7 – 2) – 5, (3 + 5) + 2) = G'(4, 10)
Hence the coordinate of the image are D'(1, 4), E'(-5, 2), F'(-2, 8), G'(4, 10)
Question 33.
LOGIC
You want to find the treasure located on the map at ![]() . You are located at
. You are located at ![]() . The following transformations will lead you to the treasure, but they are not in the correct order. Find the correct order. Use each transformation exactly once.
. The following transformations will lead you to the treasure, but they are not in the correct order. Find the correct order. Use each transformation exactly once.
- Rotate 180° about the origin.
- Reflect in the y-axis.
- Rotate 90° counterclockwise about the origin.
- Translate 1 unit right and 1 unit up.

Answer:
The correct order of transformation to get the treasure are:
- Rotate 180° about the origin.
- Rotate 90° counterclockwise about the origin.
- Reflect in the y-axis.
- Translate 1 unit right and 1 unit up.
Question 34.
DIG DEEPER!
You rotate a triangle 90° counterclockwise about the origin. Then you translate its image 1 unit left and 2 units down. The vertices of the final image are (-5, 0), (-2, 2), and (-2, -1). What are the vertices of the original triangle?
Answer:
When a point is rotated 90 degrees counterclockwise about a given point (a, b) then its both x and y coordinate becomes opposite.
Let the three vertices of the triangle be: (x1, y1), (x2, y2), (x3, y3)
P(x, y) = P'(-y, x)
Rotating 90 degrees counterclockwise about the origin:
A(x1, y1) = A'(-y1, x1)
B(x2, y2) = B'(-y2, x2)
C(x3, y3) = C'(-y3, x3)
Now translating the image of the vertex for the final image
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to the y-coordinate of the vertices.
A(x, y) = A'(x + a, y + b)
Given,
A'(-y1, x1), B'(-y2, x2), C'(-y3, x3) and a = -1, b = -2
A'(-y1 + a, x1 + b) = A”(-y1 – 1, x1 – 2)
B'(-y2 + a, x2 + b) = B”(-y2 – 1, x2 – 2)
C'(-y3 + a, x3 + b) = C”(-y3 – 1, x3 – 2)
The given coordinate of vertex point of final image are: (-5, 0), (-2, 2) and (-2, -1)
Now comparing the coordinate of the final image
(-y1 – 1, x1 – 2) = (-5, 0) so y1 = 4 and x1 = 2
(-y2 – 1, x2 – 2) = (-2, 2) so y2 = 1 and x2 = 4
(-y3 – 1, x3 – 2) = (-2, 1) so y3 = 1 and x3 = 1
Hence the vertices of original triangle are (2, 4), (4, 1) and (1, 1)
Lesson 2.4 Congruent Figures
EXPLORATION 1
Work with a partner.
a. For each pair of figures whose vertices are given below, draw the figures in a coordinate plane. Then copy one of the figures onto a piece of transparent paper. Use transformations to try to obtain one of the figures from the other figure.
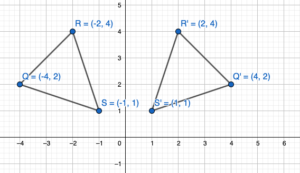
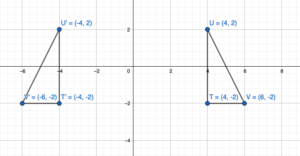
- A(-5, 1), B(-5, -4), C(-2, -4) and D(1, 4), E(1, -1), F(-2, -1)
- G(1, 2), H(2, -6), J(5, 0) and L(-1, -2), M(-2, 6), N(-5, 0)
- P(0, 0), Q(2, 2), R(4, -2) and X(0, 0), Y(3, 3), Z(6, -3)
- A(0, 4), B(3, 8), C(6, 4), D(3, 0) and
F(-4, -3), G(-8, 0), H(-4, 3), J(0, 0) - P(-2, 1), Q(-1, -2), R(1, -2), S(1, 1) and
W(7, 1), X(5, -2), Y(3, -2), Z(3, 1)
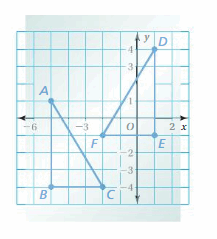

b. Which pairs of figures in part(a) are identical? Explain your reasoning.
c. FigureA and FigureB are identical. Do you think there must be a sequence of transformations that obtains Figure A from Figure B? Explain your reasoning.
2.4 Lesson
Try It
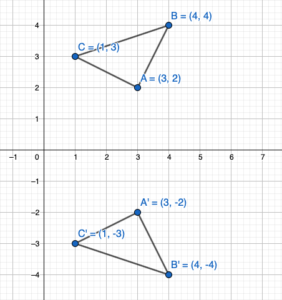
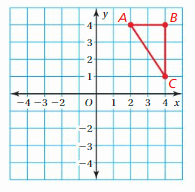
Question 1.
A triangle has vertices X(0, 4), Y(4, 4), and Z(4, 2). Is △XYZ congruent to any of the triangles in Example 1? Explain.
Answer:
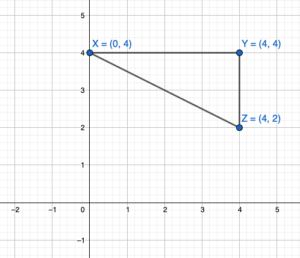
After plotting the triangle XYZ on the coordinate plane we can say that the triangle XYZ is congruent to triangle PQR among all the given triangle in the figure. In fact, if triangle PQR is rotated 90 degrees clockwise of 270 degrees counterclockwise it will result in the triangle XYZ.
Try It
Question 2.
Describing a different Sequence of rigid motions between the figures.
Answer:
Different sequence of rigid motion to get the blue figure from the red figure are:
1. First rotate the red figure 90 degrees clockwise and the origin.
2. Then translate the image 4 units Right and 1 unit Up.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
IDENTIFYING CONGRUENT FIGURES
Use the coordinate plane shown.
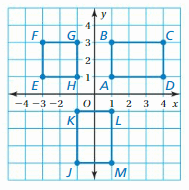
a. Identify any congruent figures.
Answer: a. After seeing the figure we can say that triangle ABCD is congruent to triangle JKLM.
b. A rectangle has vertices W(4, 1), X(4, 2), Y(1, 2), and Z(-1, -1). Is Rectangle WXYZ congruent to any of the rectangles in the coordinate plane? Explain.
Answer:
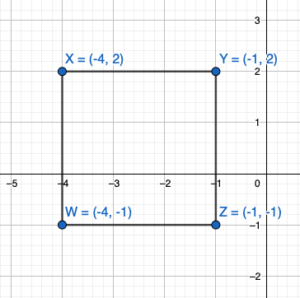
Rectangle WXYZ is not congruent to any of the rectangles in the given figure because rectangle WXYZ is square of 3 units sides and the other rectangle in the figure does not have all the sides of 3 units.
RIGID MOTIONS
The red figure is congruent to the blue figure. Describe a sequence of rigid motions between the figures.
Question 4.
Answer:
The sequence of the rigid motions from the red-figure to the blue figure:
1. First we will rotate the red figure 180 degrees clockwise or anticlockwise about the origin because the given red figure in the 4th quadrant and the blue figure is in the 2nd quadrant.
2. Then we will translate the image 1 unit left because one vertex (-1,-4) of red figure is on the negative side of the x-axis.
Question 5.
Answer:
The sequence of the rigid motions from red figure to blue figure:
1. First we will rotate the red figure 90 degrees clockwise about the origin because the given red figure in the 1st quadrant.
2. Then we will translate the image 3 units right and 1 unit down.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
In the coordinate plane at the left, each grid line represents 50 feet. Each figure represents a pasture.
a. Are the figures congruent? Use rigid motions to justify your answer.
Answer: No the blue figure and red figure are not congruent.
Explanation:
By reflecting the red figure about the y-axis and translating the image 4 units Up we will not the same blue figure. So both figure are not congruent to each other.
b. How many feet of fencing do you need to enclose each pasture?
Answer:
Given the length of each grid line = 50 feet
Total feet of fencing = 50 × total number of grid line along the boundary
For red figure fencing: 50 × 12 = 600 feet
For blue figure fencing: 50 × 12 = 600 feet
Question 7.
A home decorator uses a computer to design a floor tile. How can the decorator transform the tile as shown?
Answer:
First, rotate the given tiles about 90 degrees in the clockwise direction and then take the mirror image about the vertical axis.
Congruent Figures Homework & Practice 2.4
Review & Refresh
The vertices of a figure are given. Rotate the figure as described. Find the coordinates of the image.
Question 1.
A(1, 3), B(2, 5), C(3, 5), D(2, 3)
90° counterclockwise about the origin
Answer:
When a point is rotated 90 degrees about the origin then both x and y-coordinates become opposite.
A(x, y) = A'(-y, x)
Given,
A(1, 3), B(2, 5), C(3, 5), D(2, 3)
Rotating 90 degrees counterclockwise about the origin:
A(1, 3) = A'(-3, 1)
B(2, 5) = B'(-5, 2)
C(3, 5) = C'(-5, 3)
D(2, 3) = D'(-3, 2)
Hence the coordinate of the image are A'(-3, 1), B'(-5, 2), C'(-5, 3), D'(-3, 2)
Question 2.
F(-2, 1), G(-1, 3), H(3, 1)
180° about the origin
Answer:
When a point is rotated 180 degrees about the origin then both x and y-coordinates become opposite.
A(x, y) = A'(-x, -y)
Given,
F(-2, 1), G(-1, 3), H(3, 1)
Rotating 90 degrees counterclockwise about the origin:
F(-2, 1) = F'(2,-1)
G(-1, 3) = G'(1,-3)
H(3, 1) = H'(-3,-1)
Hence the coordinate of the image are F'(2,-1), G'(1,-3), H'(-3,-1)
Factor the expression using the greatest common factor.
Question 3.
4n – 32
Answer:
4n – 32
Take 4 as a common factor.
4(n – 8)
Thus the greatest common factor is 4(n – 8)
Question 4.
3w + 66
Answer:
3w + 66
Take 3 as a common factor.
3(w + 22)
Thus the greatest common factor is 3(w + 22)
Question 5.
2y – 18
Answer:
2y – 18
Take 2 as a common factor.
2(y – 9)
Thus the greatest common factor is 2(y – 9).
Concepts, Skills, & Problem Solving
TRANSFORMING FIGURES
The vertices of a pair of figures are given. Determine whether the figures are identical. (See Exploration 1, p. 63.)
Question 6.
G(0, 0), H(3, 2), J(1, -2) and L(-1, 0), M(2, 2), N(0, -3)
Answer:
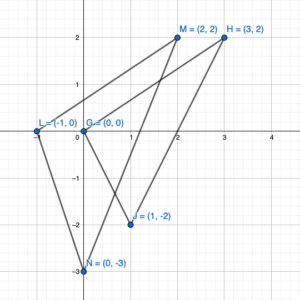
After plotting the triangles GHJ and LMN we can say that the triangle LMN are bigger compared to the other triangle. Thus both the triangles are not identical.
Question 7.
A(-2, -1), B(-2, 2), C(-1, 1), D(-1, -2) and F(-2, 0), G(-1, 1), H(2, 1), J(1, 0)
Answer:
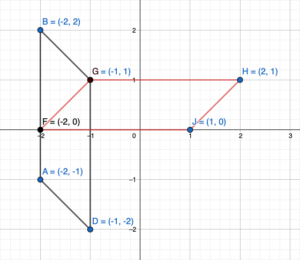
By seeing both the quadrilaterals ABCD and FGHJ we can say that they are identical.
IDENTIFYING CONGRUENT FIGURES
Identify any congruent figures in the coordinate plane.
Question 8.
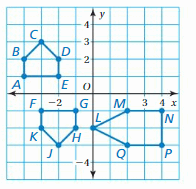
Answer:
On observing the diagram in the given figure we can see that the shape and size of pentagon ABCDE and pentagon FKJHG are the same. The length of each side of both the pentagon is the same. Thus they are congruent.
Question 9.
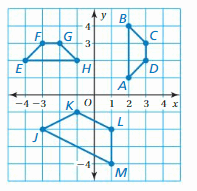
Answer:
By seeing the above figure we can say that the shape and size of parallelogram EFGH and parallelogram BCDA are the same. The length of each side of both the parallelogram are same. Parallelogram BCDA can be obtained by rotating parallelogram EFGH 90 degrees clockwise and translating its image. Hence the parallelogram, EFGH is congruent to BCDA.
DESCRIBING A SEQUENCE OF RIGID MOTIONS
The red figure is congruent to the blue figure. Describe a sequence of rigid motions between the figures.
Question 10.
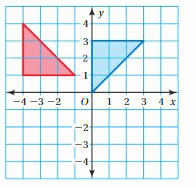
Answer:
The sequence of rigid motions between the red and blue figures are:
1. First we will rotate the red figure 90 degrees clockwise about the origin because the given red figure is in the 2nd quadrant and the blue figure is in the 1st quadrant.
2. Then we will translate the image 1 unit left and 1 unit Down because one vertex of the red figure is at (-1, 1)
Question 11.
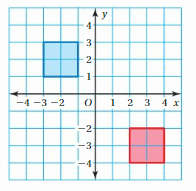
Answer:
The sequence of rigid motions between the red and blue figures are:
1. First we will rotate the red figure 180 degrees clockwise or anticlockwise about the origin because the given red figure is in 4th quadrant and the blue figure is in the 2nd quadrant.
2. Then we will translate the image 1 unit Right and 1 unit Down because one vertex of red figure is at (2, -2)
Question 12.
YOU BE THE TEACHER
Your friend describes a sequence of rigid motions between the figures. Is your friend correct? Explain your reasoning.
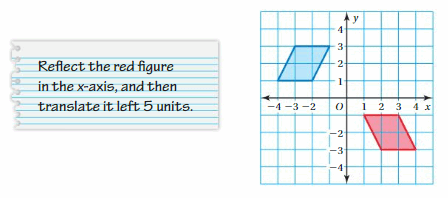
Answer:
When a point is reflected about x-axis then the y-coordinate becomes opposite.
A(x, y) = A'(x, -y)
Coordinates of red figure are A(1, -1), B(3, -1), C(4, -3), D(2, -3)
Reflection about the x-axis:
A(1, -1) = A'(1, 1)
B(3, -1) = B'(3, 1)
C(4, -3) = C'(4, 3)
D(2, -3) = D'(2, 3)
Now translating the above image point 5 unit left.
Coordinate of the vertex of blue figure are: A”(-4, 1), B”(3,1), C”(-1, 3), D”(-3,3)
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if the shift is Right and Vertical Up and the value of a and b will be negative if the shift is left and vertical Down.
Given:
A(1, 1), B(3, 1), C(4, 3), D(2, 3) and a = -5, b = 0
A”(1+a, 1+b) = A”(1-5, 1+0) = A”(-4, 1)
B”(3+a, 1+b) = B”(3-5, 1+0) = B”(-2,1)
C”(4+a,3+b) = C”(4-5, 3+0) = C”(-1, 3)
D”(2+a,3+b) = D”(2-5, 3+0) = D”(-3,3)
Hence the coordinate of image are A”(-4, 1), B”(-2,1), C”(-1, 3), D”(-3,3)
Since the coordinate of the vertex of the blue is the same in both ways.
We can say that the blue figure is obtained by the rigid motion of the red figure.
NAMING CORRESPONDING PARTS
The figures are congruent. Name the corresponding angles and the corresponding sides.
Question 13.
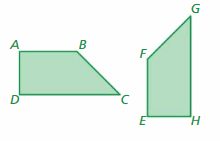
Answer:
Corresponding sides of the congruent figure are
AD = EH
AB = EF
BC = FG
CD = GH
Corresponding angles of the congruent figure are
∠A = ∠E
∠B = ∠F
∠C = ∠G
∠D = ∠H
Question 14.
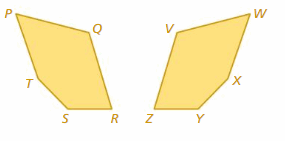
Answer:
Corresponding sides of the congruent figure are
PQ = WV
QR = VZ
RS = ZY
ST = YX
TP = XW
Corresponding angles of the congruent figure are
∠P = ∠W
∠Q = ∠V
∠R = ∠Z
∠S = ∠Y
∠T = ∠X
Question 15.
MODELING REAL LIFE
You use a computer program to transform an emoji. How can you transform the emoji as shown?
Answer:
First, take the reflection of that emoji about vertical line and then rotate that image 90 degrees clockwise to get that given emoji.
Question 16.
CRITICAL THINKING
Two figures are congruent. Are the areas of the two figures the same? the perimeters? Explain your reasoning.
Answer:
- The size of both figures should be the same.
- The shape of both the figures should be the same.
- All the corresponding angles should be the same.
- Both the area and perimeter of two congruent figures are the same.
Question 17.
DIG DEEPER!
The houses are identical.
a. What is the length of side LM?
Answer:
Length of LM = length of CD
length of CD = 32 feet
So, the length of LM is 32 feet
b.Which angle of JKLMN corresponds to ∠D?
Answer:
∠D = ∠M
Thus ∠M corresponds to ∠D
c. Side AB is congruent to side AE. What is the length of side AB? What is the perimeter of ABCDE?
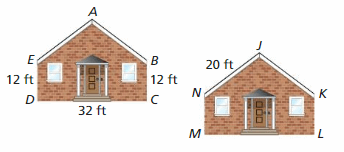 .
.
Answer:
AE = JN
The length of JN is 20 ft
So, the length of AE = 20 ft
Perimeter of ABCDE = AB + BC + CD + DE + EA
Perimeter of ABCDE = 20 + 12 + 32 + 12 + 20 = 96 feet
Thus the Perimeter of ABCDE is 96 feet
Question 18.
REASONING
Two constellations are represented by the figures in the coordinate plane shown. Are the figures congruent? Justify your answer.
Answer:
The above figure can be tranformed into below figure by rotating the figure 180 degrees clockwise or counterclockwise about the origin and translating the image 8 units Right and 8 units Up to get the above figure.
Lesson 2.5 Dilations

EXPLORATION 1
Work with a partner. Use geometry software.
a. Draw a polygon in the coordinate plane. Then dilate the polygon with respect to the origin. Describe the scale factor of the image.

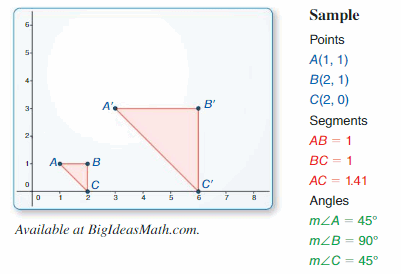
b. Compare the image and the original polygon in part(a). What do you notice about the sides? the angles?
c. Describe the relationship between each point below and the point A(x, y) in terms of dilations.
![]()
d. What are the coordinates of a point P(x, y) after a dilation with respect to the origin by a scale factor of k?
2.5 Lesson
Try It
Tell whether the blue figure is a dilation of the red figure.
Question 1.
Answer:
No the blue figure is not the dilation of the red figure.
Explanation:
Blue and red figure has same size and same shape but the blue figure is reflection about vertical axis. So, the lines corresponding vertices of both figure does not meet at a point. This means that the blue figure is not the dilation of the red figure.
Question 2.
Answer: Yes, the blue figure is a dilation of the red figure.
Explanation:
We observe that all the angles of red figure are congruent to the angles of red figure. Also their will be lines connecting the corresponding verrtices meeting at a point. This means that blue figure is dilation of the red figure.
Try It
Question 3.
WHAT IF?
Triangle ABC is dilated by a scale factor of 2. What are the coordinates of the image?
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given points of the triangle: A (1, 3), B (2, 3), C (2, 1) and scale factor = 2
Dilating the figure by scale factor of 2
A (1, 3) = A'(1 . 2, 3 . 2) = A'(2, 6)
B (2, 3) = B'(2 . 2, 3 . 2) = B'(4, 6)
C (2, 1) = C'(2 . 2, 1 . 2) = C'(4, 2)
Hence the coordinates of the image are A'(2, 6), B'(4, 6), C'(4, 2)
Try It
Question 4.
WHAT IF?
Rectangle WXYZ is dilated by a scale factor of \(\frac{1}{4}\). What are the coordinates of the image?
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given points of the rectangle: W(-4, -6), X(-4, 8), Y(4, 8), Z(4, -6)
scale factor = 0.25
W(-4, -6) = W'(-4 × 0.25, -6 × 0.25) = W'(-1, -1.5)
X(-4, 8) = X'(-4 × 0.25, 8 × 0.25) = X'(-1, 2)
Y(4, 8) = Y'(4 × 0.25, 8 × 0.25) = Y'(1, 2)
Z(4, -6) = Z'(4 × 0.25, -6 × 0.25) = Z'(1, -1.5)
Hence the coordinates of the image are W'(-1, -1.5), X'(-1, 2), Y'(1, 2), Z'(1, -1.5)
Try It
Question 5.
WHAT IF?
Trapezoid ABCDis dilated using a scale factor of 3, and then rotated 180° about the origin. What are the coordinates of the image?
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
a is the scaling factor
Given points of trapezoid: A(-2, -1), B(-1,1), C(0,1), D(0,-1) scale factor = 3
Dilating the figure by scale factor of 3
A(-2, 1) = A'(-2 . 3, -1 . 3) = A'(-6, -3)
B(-1, 1) = B'(-1 . 3, 1 . 3) = B'(-3, 3)
C(0, 1) = C'(0 . 3, 1 . 3) = C'(0, 3)
D(0, -1) = D'(0 . 3, -1 . 3) = D'(0, -3)
Thus the coodrinate of the image are A'(-6, -3), B'(-3, 3), C'(0, 3), D'(0, -3)
when a point is rotated 180 degrees about the origin then both x and y coordinate becomes opposite.
P(x, y) = P'(-x, -y)
Image points: A'(-6, -3), B'(-3, 3), C'(0, 3), D'(0, -3)
Rotating 180 degrees about the origin:
A'(-6, -3) = A”(6, 3)
B'(-3, 3) = B”(3, -3)
C'(0, 3) = C”(0, -3)
D'(0, -3) = D”(0, 3)
Thus the coodrinate of the image are A”(6, 3), B”(3, -3), C”(0, -3), D”(0, 3)
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
IDENTIFYING A DILATION
Tell whether the blue figure is a dilation of the red figure.
Question 6.
Answer: Yes, the blue figure is a dilation of the red figure.
Explanation:
We observe that all the angles of red figure are congruent to the angles of red figure. Also their will be lines connecting the corresponding vertices meeting at a point. This means that blue figure is dilation of the red figure.
Question 7.
Answer: No the blue figure is not the dilation of the red figure.
Explanation:
Blue and red figure has same size and same shape but the blue figure is reflection about vertical axis. So, the lines corresponding vertices of both figure does not meet at a point. This means that the blue figure is not the dilation of the red figure.
Question 8.
DILATING A FIGURE
The vertices of a rectangle are J(4, 8), K(12, 8), L(12, 4), and M(4, 4). Draw the image after a dilation with a scale factor of \(\frac{1}{4}\). Identify the type of dilation.
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
a is scale factor
Given, vertices of a rectangle are J(4, 8), K(12, 8), L(12, 4), and M(4, 4), scale factor = 0.25
J(4, 8) = J'(4 × 0.25, 8 × 0.25) = J'(1, 2)
K(12, 8) = K'(12 × 0.25, 8 × 0.25) = K'(3, 2)
L(12, 4) = L'(12 × 0.25, 4 × 0.25) = L'(3, 1)
M(4, 4) = M'(4 × 0.25, 4 × 0.25) = M'(1, 1)
Hence the coordinates of the image are J'(1, 2), K'(3, 2), L'(3, 1), M'(1, 1)
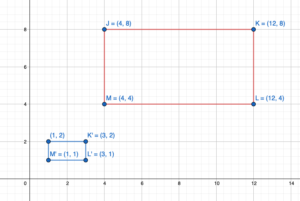
Question 9.
VOCABULARY
How is a dilation different from other transformations?
Answer:
The difference between dilation and other transformations are
- In the case of dilate the size of the figure after the dilation either decrease or increase but the shape of the figure before and after dilation remains same. Also after the dilation the corresponding angles will be congruent.
- In case of other transformations such as Rotation, translation, reflection the shape and size of figure before and after transformation remains the same.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
A photograph is dilated to fit in a frame, so that its area after the dilation is 9 times greater than the area of the original photograph. What is the scale factor of the dilation? Explain.
Answer: The scale factor of length and breadth will be 3.
Explanation:
Given,
The area after the dilation is 9 times greater than the area of the original photograph.
Area = length × breadth
p = 3 × 3
Hence the scale factor of length and breadth will be 3.
Question 11.
DIG DEEPER!
The location of a water treatment plant is mapped using a coordinate plane, where each unit represents 1 foot. The plant has vertices (0, 0), (0, 180), (240, 180), and (240, 0). You dilate the figure with a scale factor of \(\frac{1}{3}\). What are the coordinates of the image? What do you need to change so that the image accurately represents the location of the plant? Explain your reasoning.

Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
a is the scaling factor
Location of water treatment plant: A(0, 0), B(0, 180), C(240, 180), D(240, 0)
scale factor = \(\frac{1}{3}\)
Dilating the figure by scale factor of \(\frac{1}{3}\)
A(0, 0) = A'(0 × \(\frac{1}{3}\), 0 × \(\frac{1}{3}\)) = A'(0, 0)
B(0, 180) = B'(0 × \(\frac{1}{3}\), 180 × \(\frac{1}{3}\)) = B'(0, 60)
C(240, 180) = C'(240 × \(\frac{1}{3}\), 180 × \(\frac{1}{3}\)) = C'(80, 60)
D(240, 0) = D'(240 × \(\frac{1}{3}\), 0 × \(\frac{1}{3}\)) = D'(80, 0)
Hence the coordinates of the image are A'(0, 0), B'(0, 60), C'(80, 60), D'(80, 0)
Dilations Homework & Practice 2.5
Review & Refresh
The red figure is congruent to the blue figure. Describe a sequence of rigid motions between the figures.
Question 1.
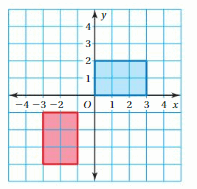
Answer:
Sequence of rigid motion between the red and blue figure are
1. First rotate the blue figure 90 degrees in counterclockwise direction about the orgin because blue figure in 1st quadrant and red figure is in 3rd quadrant.
2. Then translate the image 1 unit left and 4 units down.
Question 2.
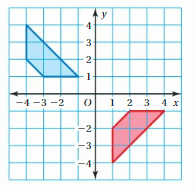
Answer:
Sequence of rigid motion between the red and blue figure are
1. First reflect the blue fiure about x-axis. The image after the reflection will lies in the 3rd quadrant with same orientation.
2. Then translate the image 5 units Right.
Tell whether the ratios form a proportion.
Question 3.
3 : 5 and 15 : 20
Answer:
When two ratios are equal then it is called as proportion.
Given,
Given 3 : 5 and 15 : 20
3/5 and 15/20
3/5 and 3/4
Since the above two ratio are not equal hence they are not proportion
Question 4.
2 to 3 and 12 to 18
Answer:
When two ratios are equal then it is called as proportion.
Given,
2 to 3 and 12 to 18
2/3 and 12/18
2/3 and 2/3
Since the above two ratio are equal hence they are proportion.
Question 5.
7 : 28 and 12 : 48
Answer:
When two ratios are equal then it is called as proportion.
Given,
7 : 28 and 12 : 48
7/28 and 12/48
1/4 and 1/4
Since the above two ratio are equal hence they are proportion.
Concepts, Skills, &Problem Solving
DESCRIBING RELATIONSHIPS
Describe the relationship between the given point and the point A(8, 12) in terms of dilations. (See Exploration 1, p. 69.)
Question 6.
B(16, 24)
Answer:
Given a point and its image: A(8,12), B(16, 24)
Here we can see that both x-coordinate and y-coordinate of image point have increased to double.
This means that in this case, the image figure has become larger by the scale factor of 2 with respect to the origin.
Hence the dilation scale factor is 2.
Question 7.
C(2, 3)
Answer:
Given a point and its image: A(8,12), C(2, 3)
Here we can see that both x-coordinate and y-coordinate of image point has decreased to one-fourth.
This means that in this case, the image figure has become smaller by the scale factor of 0.25 with respect to the origin.
Thus the dilation scale factor is 1/4.
Question 8.
D(6, 9)
Answer:
Given a point and its image: A(8,12), D(6, 9)
Here we can see that both x-coordinate and y-coordinate of image point has decreased to three-fourth.
This means that in this case the image figure has become smaller by the scale factor of 0.75 with respect to the origin.
Thus the dilation scale factor is 3/4.
IDENTIFYING A DILATION
Tell whether the blue figure is a dilation of the red figure.
Question 9.
Answer: Yes, the blue figure is a dilation of the red figure.
Explanation:
We observe that all the angles of the red figure are congruent to the angles of the red figure. Also there will be lines connecting the corresponding vertices meeting at a point. This means that blue figure is a dilation of the red figure.
Question 10.
Answer: Yes, the blue figure is a dilation of the red figure.
Explanation:
We observe that all the angles of the red figure are congruent to the angles of the red figure. Also there will be lines connecting the corresponding vertices meeting at a point. This means that blue figure is a dilation of the red figure.
Question 11.
Answer: No the blue figure is not the dilation of the red figure.
Explanation:
The Blue and red figure has same size and same shape but the blue figure is a reflection of vertical axis. So, the lines corresponding vertices of both figure does not meet at a point. This means that the blue figure is not the dilation of the red figure.
Question 12.
Answer: Yes, the blue figure is a dilation of the red figure.
Explanation:
We observe that all the angles of red figure are congruent to the angles of red figure. Also their will be lines connecting the corresponding vertices meeting at a point. This means that blue figure is dilation of the red figure.
Question 13.
Answer: Yes, the blue figure is a dilation of the red figure.
Explanation:
We observe that all the angles of red figure are congruent to the angles of red figure. Also their will be lines connecting the corresponding vertices meeting at a point. This means that blue figure is dilation of the red figure.
Question 14.
Answer: No the blue figure is not the dilation of the red figure.
Explanation:
Blue and red figure has same size and same shape but the blue figure is reflection about vertical axis. So, the lines corresponding vertices of both figure does not meet at a point. This means that the blue figure is not the dilation of the red figure.
DILATING A FIGURE
The vertices of a figure are given. Draw the figure and its image after a dilation with the given scale factor. Identify the type of dilation.
Question 15.
A(1, 1), B(1, 4), C(3, 1); k = 4
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given points of the triangle: A(1, 1), B(1, 4), C(3, 1) and scale factor = 4
Dilating the figure by scale factor by 4
A(1, 1) = A'(1 × 4, 1 × 4) = A'(4, 4)
B(1, 4) = B'(1 × 4, 4 × 4) = B'(4, 16)
C(3, 1) = C'(3 × 4, 1 × 4) = C'(12, 4)
Hence the coordinate of the image are A'(4, 4), B'(4, 16), C'(12, 4)
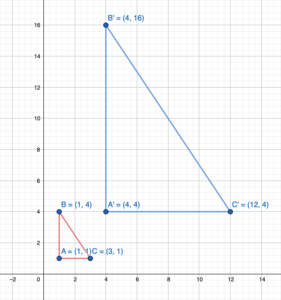
Question 16.
D(0, 2), E(6, 2), F(6, 4); k = 0.5
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given points of the triangle: D(0, 2), E(6, 2), F(6, 4) and scale factor = 0.5
Dilating the figure by scale factor by 0.5
D(0, 2) = D'(0 × 0.25, 2 × 0.25) = D'(0, 1)
E(6, 2) = E'(6 × 0.25, 2 × 0.25) = E'(3, 1)
F(6, 4) = F'(6 × 0.25, 4 × 0.25) = F'(3, 2)
Hence the coordinate of the image are D'(0, 1), E'(3, 1), F'(3, 2)
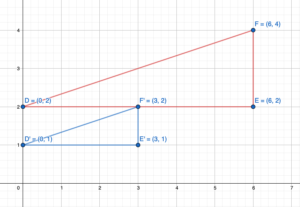
Question 17.
G(-2, -2), H(-2, 6), J(2, 6); k = 0.25
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given points of the triangle: G(-2, -2), H(-2, 6), J(2, 6) and scale factor = 0.25
G(-2, -2) = G'(-2 × 0.25, -2 × 0.25) = G'(-0.5, -0.5)
H(-2, 6) = H'(-2 × 0.25,6 × 0.25) = H'(-0.5, 1.5)
J(2, 6) = G'(2 × 0.25, 6 × 0.25) = J'(0.5, 1.5)
Hence the coordinate of the image are G'(-0.5, -0.5), H'(-0.5, 1.5), J'(0.5, 1.5)
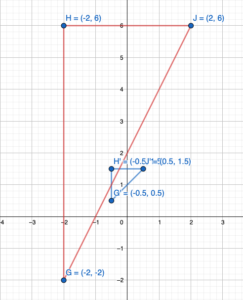
Question 18.
M(2, 3), N(5, 3), P(5, 1); k = 3
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given points of the triangle: M(2, 3), N(5, 3), P(5, 1) and scale factor = 3
M(2, 3) = M'(2 × 3, 3 × 3) = M'(6, 9)
N(5, 3) = N'(5 × 3, 3 × 3) = N'(15, 9)
P(5, 1) = P'(5 × 3, 1 × 3) = P'(15, 3)
Hence the coordinate of the image are M'(6, 9), N'(15, 9), P'(15, 3)
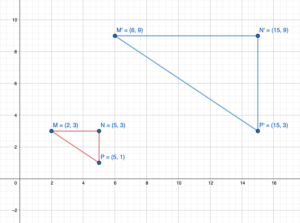
Question 19.
Q(-3, 0), R(-3, 6), T(4, 6), U(4, 0); k = \(\frac{1}{3}\)
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given,
Q(-3, 0), R(-3, 6), T(4, 6), U(4, 0) and scale factor = \(\frac{1}{3}\)
Q(-3, 0) = Q'(-3 × \(\frac{1}{3}\), 0 × \(\frac{1}{3}\)) = Q'(-1, 0)
R(-3, 6) = R'(-3 × \(\frac{1}{3}\), 6 × \(\frac{1}{3}\)) = R'(-1, 2)
T(4, 6) = T'(4 × \(\frac{1}{3}\), 6 × \(\frac{1}{3}\)) = T'(4/3, 2)
U(4, 0) = U'(4 × \(\frac{1}{3}\), 0 × \(\frac{1}{3}\)) = U'(4/3, 0)
Hence the coordinate of the image are Q'(-1, 0), R'(-1, 2), T'(4/3, 2), U'(4/3, 0)
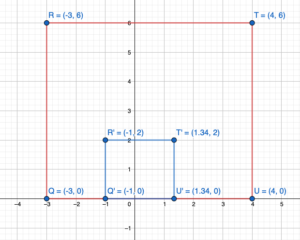
Question 20.
V(-2, -2), W(-2, 3), X(5, 3), Y(5, -2); k = 5
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given,
V(-2, -2), W(-2, 3), X(5, 3), Y(5, -2), scaling factor = 5
Dilating the figure by scale factor of 5
V(-2, -2) = V'(-2 × 5, -2 × 5) = V'(-10, -10)
W(-2, 3) = W'(-2 × 5, 3 × 5) = W'(-10, 15)
X(5, 3) = X'(5 × 5, 3 × 5) = X'(25, 15)
Y(5, -2) = Y'(5 × 5, -2 × 5) = Y'(25, -10)
Hence the coordinate of the image are V'(-10, -10),W'(-10, 15), X'(25, 15), Y'(25, -10)
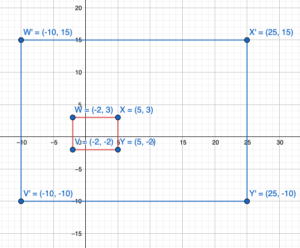
Question 21.
YOU BE THE TEACHER
Your friend finds the coordinates of the image of △ABC after a dilation with a scale factor of 2. Is your friend correct? Explain your reasoning.

Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given,
The points of triangle: A(2, 5), B(2, 0), C(4, 0)
scale factor = 2
Dilating the figure by scale factor of 2
A(2, 5) = A'(2 × 2, 5 × 2) = A'(4, 10)
B(2, 0) = B'(2 × 2, 0 × 2) = B'(4, 0)
C(4, 0) = C'(4 × 2, 0 × 2) = C'(8, 0)
Hence the coordinate of the image are A'(4, 10), B'(4, 0), C'(8, 0)
By this, we can say that my friend is correct.
FINDING A SCALE FACTOR
The blue figure is a dilation of the red figure. Identify the type of dilation and find the scale factor.
Question 22.
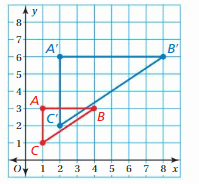
Answer:
Scale factor = side length of image/side length of original figure
Scale factor = A’B’/AB = 6/3 = 2
Scale factor = 2
Hence, type of dilation is enlargement with scale factor of 2.
Question 23.
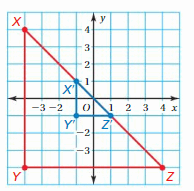
Answer:
Scale factor = side length of image/side length of original figure
Scale factor = X’Y’/XY= 2/8 = 1/4
Scale factor = 1/4
Hence, the type of dilation is reduction with the scale factor of 1/4
Question 24.
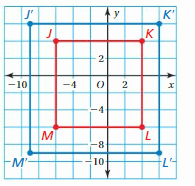
Answer:
Scale factor = side length of image/side length of the original figure
Scale factor = J’K’/JK = 15/10 = 3/2
Scale factor = 3/2
Hence, the type of dilation is reduction with the scale factor of 3/2
Question 25.
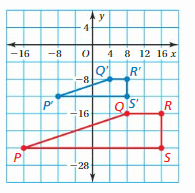
Answer:
Scale factor = side length of image/side length of original figure
Scale factor = Q’R’/QR = 4/8 = 1/2
Scale factor = 1/2
Hence, type of dilation is reduction with scale factor of 1/2
USING MORE THAN ONE TRANSFORMATION
The vertices of a figure are given. Find the coordinates of the image after the transformations given.
Question 26.
A(-5, 3), B(-2, 3), C(-2, 1), D(-5, 1)
Reflect in the y-axis. Then dilate using a scale factor of 2.
Answer:
We know that when a point is reflected about y-axis then is x-coordinate becomes opposite.
A(-5, 3), B(-2, 3), C(-2, 1), D(-5, 1)
A(x, y) = A'(-x, y)
A(-5, 3) = A'(5, 3)
B(-2, 3) = B'(2, 3)
C(-2, 1) = C'(2, 1)
D(-5, 1) = D'(5, 1)
Coordinate of the image are A'(5, 3), B'(2, 3), C'(2, 1), D'(5, 1)
A(-5, 3), B(-2, 3), C(-2, 1), D(-5, 1)
Reflect in the y-axis. Then dilate using a scale factor of 2
A'(5, 3) = A”(5 × 2, 3 × 2) = A”(10, 6)
B'(2, 3) = B”(2 × 2, 3 × 2) = B”(4, 6)
C'(2, 1) = C”(2 × 2, 1 × 2) = C”(4, 2)
D'(5, 1) = D”(5 × 2, 1 × 2) = D”(10, 2)
Coordinate of the image are A”(10, 6), B”(4, 6), C”(4, 2), D”(10, 2)
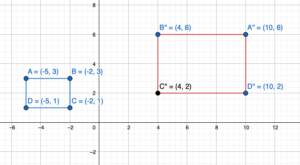
Question 27.
F(-9, -9), G(-3, -6), H(-3, -9).
Dilate using a scale factor of \(\frac{2}{3}\). Then translate 6 units up.
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given,
F(-9, -9), G(-3, -6), H(-3, -9) and scale factor of \(\frac{2}{3}\)
Dilating the figure by scale factor of \(\frac{2}{3}\)
F(-9, -9) = F'(-9 × 2/3, -9 × 2/3) = F'(-6, -6)
G(-3, -6) = G'(-3 × 2/3, -6 × 2/3) = G'(-2, -4)
H(-3, -9) = H'(-3 × 2/3, -9 × 2/3) = H'(-2, -6)
Coordinate of the image are F'(-6, -6), G'(-2, -4), H'(-2, -6)
Now translating above image 6 units up
F'(-6, -6), G'(-2, -4), H'(-2, -6) and a = 0, b = 6
F”(-6 + a, -6 + b) = F”(-6 + 0, -6 + 6) = F”(-6, 0)
G”(-2 + a, -4 + b) = G”(-2 + 0, -4 + 6) = G”(-2, 2)
H”(-2 + a, -6 + b) = H”(-2 + 0, -6 + 6) = H”(-2, 0)
Coordinate of the image are F”(-6, 0), G”(-2, 2), H”(-2, 0)
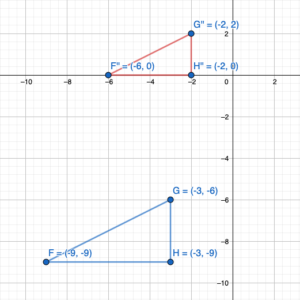
Question 28.
J(1, 1), K(3, 4), L(5, 1)
Rotate 90° clockwise about the origin. Then dilate using a scale factor of 3.
Answer:
The rotation of an object 90 degrees clockwise is equal to the rotation of 270 degrees counterclockwise.
When a point is rotated 270 degrees counterclockwise about the origin then both x and y-coordinates gets interchanged and the x-coordinate becomes the opposite.
A(x, y) = A'(y, -x)
J(1, 1), K(3, 4), L(5, 1)
Rotate 90° clockwise about the origin.
J(1, 1) = J'(1, -1)
K(3, 4) = K'(4, -3)
L(5, 1) = L'(1, -5)
Coordinate of the image are J'(1, -1), K'(4, -3), L'(1, -5)
Now dilate using a scale factor of 3.
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
J'(1, -1) = J”(1 . 3, -1 . 3) = J”(3, -3)
K'(4, -3) = K”(4 . 3, -3 . 3) = K”(12, -9)
L'(1, -5) = L”(1 . 3, -5 . 3) = L”(3, -15)
Coordinate of the image are J”(3, -3), K”(12, -9), L”(3, -15)
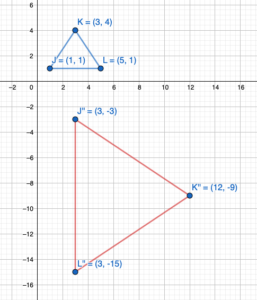
Question 29.
LOGIC
You can use a flashlight and a shadow puppet (your hands) to project shadows on the wall.
a. Identify the type of dilation.p
Answer: The type of dilation is an enlargement
b. What does the flashlight represent?
Answer: Flashlight represents center of dilation because all the line connecting shadow and hand meet at the flashlight.
c. The length of the ears on the shadow puppet is 3 inches. The length of the ears on the shadow is 4 inches. What is the scale factor?
Answer: Scale factor = length of ears on shadow/length of ears on puppet
Scale factor = 4/3
d. Describe what happens as the shadow puppet moves closer to the flashlight. How does this affect the scale factor?

Answer:
As the flashlight will move closer the shadow will become larger. Also, the scale factor will increase.
Question 30.
REASONING
A triangle is dilated using a scale factor of 3. The image is then dilated using a scale factor of \(\frac{1}{2}\). What scale factor can you use to dilate the original triangle to obtain the final image? Explain.
Answer:
Given the first scale factor of triangle S1 = 3
Given second scale factor of triangle S2 = 1/2
We know that the final scale factor S = S1 × S2
Final Scale factor S = 3 × 1/2 = 3/2
Hence, the scale factor of the final image will be the multiplication of the first and second dilation scale factor and the final scale factor will be 3/2.
CRITICAL THINKING
The coordinate notation shows how the coordinates of a figure are related to the coordinates of its image after transformations. What are the transformations? Are the figure and its image congruent? Explain.
Question 31.
(x, y) → (2x + 4, 2y – 3)
Answer:
Given, (x, y) → (2x + 4, 2y – 3)
We can see that both x-coordinate and y-coordinate has been multiplied by 2 this means that the point has been dilated by the scale factor of 2.
Also, 4 has been added to x-coordinate while 3 is added to y-coordinate which means that obtained after the dilation has been translated 4 unit Right and 3 units Down.
The final image will not be congruent because after the dilation the size of the image either increases or decreases that depend on the type of dilation.
Question 32.
(x, y) → (-x – 1, y – 2)
Answer:
Given, (x, y) → (-x – 1, y – 2)
We can see that 1 has been subtracted from x-coordinate while 2 is subtracted from y-coordinate which means that will image has translated 1 unit left and 2 units down. And also x-coordinate is opposite which means the image has been reflected about the y-axis.
Hence, transforms translation of 1 unit left and 2 units down followed by reflection about y-axis.
Question 33.
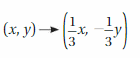
Answer:
Given, (x, y) → (1/3x, -1/3y)
We can see that both x-coordinate and y-coordinate has been multiplied by 2 this means that the point has been dilated by the scale factor of 1/3. Also, y-coordinate is opposite which means that image obtained after the dilation has been reflected about the x-axis.
Thus transforms are dilation with the scale factor of 1/3 followed by reflection about the x-axis.
STRUCTURE
The blue figure is a transformation of the red figure. Use coordinate notation to describe the transformation. Explain your reasoning.
Question 34.
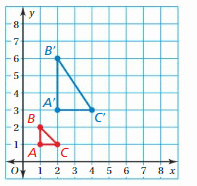
Answer:
Coordinates of original figure A(1, 1) B(1, 2), C(2, 1)
Coordinates of red figure A'(2, 3) B'(2, 6), C'(4, 3)
Scale factor of x-coordinate = x-coordinate of image/x-coordinate of image = 2/1 = 2
Scale factor of y-coordinate = y-coordinate of image/y-coordinate of image = 3/1 = 3
Thus to transfer the red-figure into the blue figure x-coordinate of all the points has been multiplied by 2 and the y-coordinate of all the points has been multiplied by 3.
Question 35.
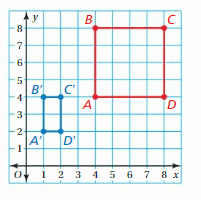
Answer:
Coordinates of original figure A(4, 4) B(4, 8), C(8, 8), D(8, 4)
Coordinates of red figure A'(1, 2) B'(1, 4), C'(2, 4), D'(2. 2)
Scale factor of x-coordinate = x-coordinate of image/x-coordinate of image = 1/4 = 0.25
Scale factor of y-coordinate = y-coordinate of image/y-coordinate of image = 2/4 = 1/2 = 0.5
Thus to transfer the red figure into the blue figure x-coordinate of all the points has been multiplied by 0.25 and the y-coordinate of all the points has been multiplied by 0.50
Question 36.
NUMBER SENSE
You dilate a figure using a scale factor of 2, and then translate it 3 units right. Your friend translates the same figure 3 units right and then dilates it using a scale factor of 2. Are the images congruent? Explain.
Answer:
Blue the final image in both the case will be of the same shape and size.
Yes, the image in both cases will be the same.
Question 37.
PROBLEM SOLVING
The vertices of a trapezoid are A(-2, 3), B(2, 3), C(5, -2), and D(-2, -2). Dilate the trapezoid with respect to vertex A using a scale factor of 2. What are the coordinates of the image? Explain the method you used.
Answer:
When the points of a given figure are dilated about a point we simply multiply the distance of each side by the given scale factor. The coordinate of one point remains the same about which dilation occurs.
The vertices of a trapezoid are A(-2, 3), B(2, 3), C(5, -2), and D(-2, -2).
Scale factor = 2
So, here the coordinate of point A(-2, 3) will remains the same but all the other coordinates of points B’, C’, D’ will change according to the distance between each side of the trapezoid.
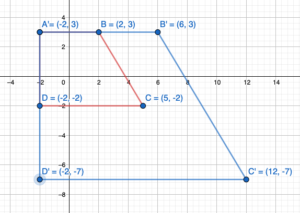
Image of the figure after dilating by a scale factor of 2
A(-2, 3) = A'(-2, 3)
B(2, 3) = B'(6, 3)
C(5, -2) = C'(12, -7)
D(-2, -2) = D'(-2, -7)
Thus the coordinate of the image are A'(-2, 3), B'(6, 3), C'(12, -7), D'(-2, -7)
Question 38.
DIG DEEPER!
A figure is dilated using a scale factor of -1. How can you obtain the image without using a dilation? Explain your reasoning.
Answer:
When a figure is dilated using a scale factor of -1 then both the x and y-coordinate of the image will become opposite.
Example:
A'(x . -1, y . -1) = A'(-x, -y)
But there are two ways to get the same image:
1. By rotating the figure 180 degrees clockwise or anticlockwise
A(x, y) rotating 180 degrees about the origin = A'(-x, -y)
2. By rotating the figure about the x-axis and y axis
A(x, y) reflecting about the origin = A'(-x, -y)
Lesson 2.6 Similar Figures
EXPLORATION 1
Work with a partner. Use geometry software.
a. For each pair of figures whose vertices are given below, draw the figures in a coordinate plane. Use dilations and rigid motions to try to obtain one of the figures from the other figure.
- A(-3, 6), B(0, -3), C(3, 6) and G(-1, 2), H(0, 1), J(1, 2)
- D(0, 0), E(3, 0), F(3, 3) and L(0, 0), M(0, 6), N(-6, 6)
- P(1, 0), Q(4, 2), R(7, 0) and X(-1, 0), Y(-4, 6), Z(-7, 0)
- A(-3, 2), B(-1, 2), C(-1, -1), D(-3, -1) and F(6, 4), G(2, 4), H(2, -2), J(6, -2)
- P(-2, 2), Q(-1, -1), R(1, -1), S(2, 2) and W(2, 8), X(3, 3), Y(7, 3), Z(8, 8)

b. Is a scale drawing represented by any of the pairs of figures in part(a)? Explain your reasoning.
c. Figure A is a scale drawing of Figure B. Do you think there must be a sequence of transformations that obtains Figure A from Figure B? Explain your reasoning.
2.6 Lesson
Try It
Question 1.
A triangle has vertices D(0, 4), E(5, 4), and F(5, 0). Is △DEF similar to △ABC and △JKL in Example 1? Explain.
Answer:
Given coordinate of the triangle ABC: A(0, 3), B(3, 3), C(3, 0)
Given coordinate of the triangle DEF: D(0, 4), E(5, 4), F(5, 0)
Given coordinate of the triangle JKL: J(0, 6), K(6, 6), L(6, 0)
Here we can see that there is no fixed relation between the coordinate between triangle ABC and DEF or triangle ABC and JKL. So no triangle is dilation with the triangle ABC.
Hence, triangle ABC is not similar △DEF and △JKL.
Try It
Question 2.
Can you reflect the red figure first, and then perform the dilation to obtain the blue figure? Explain.
Answer:
Because the final image will not depend on the order of transformation. When we will first reflect red figure then the image will be of the same size and after the dilation of the image obtained after reflection we will get the same image so we can use any two method but the final image will be the same
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
IDENTIFYING SIMILAR FIGURES
In the coordinate plane at the left, determine whether Rectangle ABCD is similar to Rectangle EFGH. Explain your reasoning.
Answer: No rectangle ABCD is not similar to rectangle EFGH
Explanation:
Because the orientation of rectangle ABCD is not the same as the rectangle EFGH. Also, rectangle ABCD is not dilated with rectangle EFGH. So there is no similarity transformation between rectangle ABCD and rectangle EFGH.
Question 4.
SIMILARITY TRANSFORMATION
The red triangle is similar to the blue triangle. Describe a similarity transformation between the figures.
Answer:
Coordinate of left vertex of the red triangle: A(5, 5)
Coordinate of the same vertex after dilation: A'(10, 10)
Now coordinate left vertex of the blue triangle: A”(0, 2)
So, the value of a = 0 – 10 = -10 and b = 2 – 10 = -8
It is given that the red triangle is similar to the blue triangle so the steps of transformation:
First, dilate the figure by the scale factor of 2 and then translate the image 10 units left and 8 units down.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
A medical supplier sells gauze in large and small rectangular sheets. A large sheet has a length of 9 inches and an area of 45 square inches. A small sheet has a length of 4 inches and a width of 3 inches. Are the sheets similar? Justify your answer.
Answer:
Condition for the rectangular sheets to be similar is that all the corresponding sides of bigger and smaller rectangular sheets should be in proportional.
Area of larger rectangular sheets a = 45 sq in
length of larger rectangular sheets l1 = 9 in
Width = a/l = 45/9 = 5 in
length of smaller rectangular sheets l2 = 4 in
width of smaller rectangular sheets b2 = 3 in
condition for similarity l1/l2 = b1/b2
9/4 ≠ 5/3
These sheets are not similar
Question 6.
The sail on a souvenir boat is similar in shape to the sail on a sailboat. The sail on the sailboat is in the shape of a right triangle with a base of 9 feet and a height of 24 feet. The height of the souvenir’s sail is 3 inches. What is the base of the souvenir’s sail?

Answer:
Given,
The base of sail on sailboat b1 = 9 ft
height of sail on sailboat h1 = 24 ft
Given height of sail on souvenir boat: h2 = 3in = 0.25 ft
h1/h2 = b1/b2
24/0.25 = 9/h2
h2 = (9 × 0.25)/24 = 0.9375 ft = 1.125 in
Thus the height of sail of a souvenir boat is 1.125 in
Question 7.
DIG DEEPER!
A coordinate plane is used to represent a cheerleading formation. The vertices of the formation are A(4, 4), B(0, 8), C(4, 4), and D(0, 6). A choreographer creates a new formation similar to the original formation. Three vertices of the new formation are J(-2, -2), K(0, -4), and L(2, -2). What is the location of the fourth vertex? Explain.
Answer:
The vertices of the formation are A(4, 4), B(0, 8), C(4, 4), and D(0, 6). A choreographer creates a new formation similar to the original formation.
We observe the image point carefully that both the x and y coordinate of the image point is just half of the original point and each y-coordinate is opposite.
A(4, 4) = J(-2, -2)
B(0, 8) = K(0, -4)
C(4, 4) = L(2, -2)
D(0, 6) = M(x, y)
This means that the point A, B, C are dilated by using a scale factor of 0.5 and the image obtained from the dilation is reflected about the x-axis.
So, the image point is D(0, 6) = M(0, -3)
Similar Figures Homework & Practice 2.6
Review & Refresh
Tell whether the blue figure is a dilation of the red figure.
Question 1.
Answer: No
Explanation:
Because the shape and size of both red and blue figure are the same which is not the property of dilation. The blue figure is the result of the reflection of the red figure 180 degrees in the clockwise or counterclockwise direction.
Question 2.

Answer: Yes
Explanation:
When we see both red and blue figures closely we observe that all the angles of the red figure are congruent to the blue figure. Also, there will be the lines connecting corresponding vertices meeting at a point. This means that the blue figure is a dilation of red figure.
Question 3.
You solve the equation S = lw + 2wh for w. Which equation is correct?

Answer: Option C
Explanation:
S = lw + 2wh
lw + 2wh = S
Taking w as a common factor
w(l + 2h) = s
w = s/(l + 2h)
Thus the correct answer is option C.
Concepts, Skills, &Problem Solving
TRANSFORMING FIGURES
The vertices of a pair of figures are given. Determine whether a scale drawing is represented by the pair of figures. (See Exploration 1, p. 77.)
Question 4.
A(-8, -2), B(-4, 2), C(-4, -2) and G(2, -1), H(4, -1), J(2, -3)
Answer: Yes
Explanation:
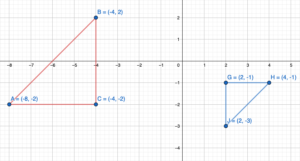
After plotting both triangles we see that the original figure is exactly double of the image. Each side of the original triangle is double the length of the image triangle. So given vertices pair represent a scale drawing.
Scale factor = 2
Question 5.
A(0, 3), B(3, 4), C(5, 3), D(3, 2) and F(-4, 4), G(-1, 5), H(5, 3), J(3, 2)
Answer: No
Explanation:
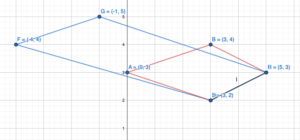
After plotting both given figures we can see that there is no transformation relation between the original figure and the image figure. So, the given vertices pair does not represent a scale drawing.
IDENTIFYING SIMILAR FIGURES
Determine whether the figures are similar. Explain your reasoning.(See Exploration 1, p. 77.)
Question 6.
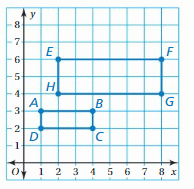
Answer: Rectangle ABCD is similar to rectangle EFGH.
Explanation:
Because when you see both the given figure we can see that all the corresponding angles of rectangle ABCD and rectangle EFGH are equal. And also the corresponding sides of both rectangle are in proportional.
∠A = ∠E, ∠B = ∠F, ∠C = ∠G, ∠D = ∠H
AB/EF = BC/FG = GH/CD = DA/HE = 1/2
Hence rectangle ABCD is similar to rectangle EFGH.
Question 7.
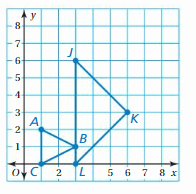
Answer: Both the triangle are not similar
Explanation:
Because when you see both the given figure we can see that all the corresponding angles of triangle ABC and triangle JKL are equal. And also the corresponding sides of both triangles are not proportional.
AB/JK ≠ KL/BC ≠ CA/LJ
Hence triangle ABC is not similar to triangle JKL
IDENTIFYING SIMILAR FIGURES
Draw the figures with the given vertices in a coordinate plane. Which figures are similar? Explain your reasoning.
Question 8.
Rectangle A: (0, 0), (4, 0), (4, 2), (0, 2)
Rectangle B: (0, 0), (6, 0), (6, 3), (0, 3)
Rectangle C: (0, 0), (4, 0), (4, 2), (0, 2)
Answer: Rectangle A and B are similar
Explanation:
Rectangle A: (0, 0), (4, 0), (4, 2), (0, 2)
Rectangle B: (0, 0), (6, 0), (6, 3), (0, 3)
Rectangle C: (0, 0), (4, 0), (4, 2), (0, 2)
By seeing the above figure we can say that rectangle A and rectangle B are similar and rectangle A and Rectangle C are congruent.
Question 9.
FigureA: (4, 2), (2, 2), (2, 0), (4, 0)
Figure B: (1, 4), (4, 4), (4, 1), (1, 1)
Figure C: (2, 1), (5, 1), (5, 3), (2, 3)
Answer: Rectangle A and B are similar
Explanation:
FigureA: (4, 2), (2, 2), (2, 0), (4, 0)
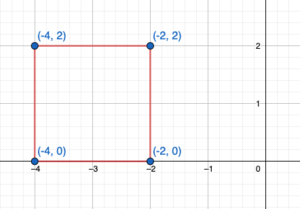
Figure B: (1, 4), (4, 4), (4, 1), (1, 1)
Figure C: (2, 1), (5, 1), (5, 3), (2, 3)
Rectangles A and B are similar because in rectangle A and B all the corresponding angles are equal and also all the corresponding sides are equal.
DESCRIBING A SIMILARITY TRANSFORMATION
The red figure is similar to the blue figure. Describe a similarity transformation between the figures.
Question 10.
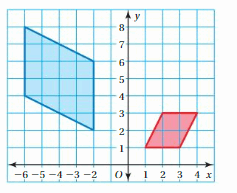
Answer:
1. First rotate the red figure 90 degrees anticlockwise because the red figure is in the first quadrant and the blue figure is in the second quadrant.
2. Then dilate the image obtained after the rotation by the scale factor of 2 because the blue figure is double the size of the red figure.
Scale factor = side of the image/side of the original figure = 4/2 = 2
Question 11.
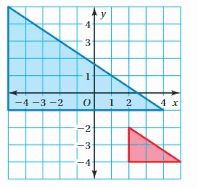
Answer:
First, dilate the red figure by the scale figure of 3 because the blue figure is triple the size of red figure.
scale factor = side of image/side of original figure = 6/2 = 3
Question 12.
MODELING REAL LIFE
A barrier in the shape of a rectangle is used to retain oil spills. On a blueprint, a similar barrier is 9 inches long and 2 inches wide. The width of the actual barrier is 1.2 miles. What is the length of the actual barrier?

Answer:
Given,
Width of the actual barrier = 1.2 miles
Width of the barrier in the blueprint = 2 inches
2 inch dimension of blueprint = 1.2 miles of original
So, 1 inch dimension of blueprint = 1.2/2 = 0.6 miles.
Since the length of the barrier in the blueprint = 9 inches,
Thus the length of the actual barrier = 9(0.6) = 5.4 miles.
Question 13.
LOGIC
Are the following figures always, sometimes, or never similar? Explain.
a. two triangles
b. two squares
c. two rectangles
Answer:
a. Two triangles sometimes two triangles are similar when all the corresponding angles are equal and all the corresponding sides lengths are in proportion.
b. Two squares always two square are similar only when all the sides are proportional and all the angles are equal.
c. Two rectangles are similar when all the corresponding angles are equal but the lengths of the corresponding sides are not always in proportion.
Question 14.
CRITICAL THINKING
Can you draw two quadrilaterals each having two 130° angles and two 50° angles that are not similar? Justify your answer.
Answer:
Quadrilateral 1: 50°, 50°, 130°, 130° (trapezoid)
Quadrilateral 2: 50°, 130°, 50°, 130° (parallelogram)
Question 15.
REASONING
The sign is rectangular.
a. You increase each side length by 20%. Is the new sign similar to the original? Explain your reasoning.
Answer:
Given,
You increase each side length by 20%
Scale factor = 1 + percentage increase/100 = 1 + 20/100 = 1.2
b. You increase each side length by 6 inches. Is the new sign similar to the original? Explain your reasoning.
Answer:
No, because when length and width are of a different size then adding 6 inches on each side will not increase the figure in a fixed proportion. So the corresponding length will be not proportional. This means that both the figure will be not in dilation, hence not similar.
Question 16.
DIG DEEPER!
A person standing 20 feet from a streetlight casts a shadow as shown. How many times taller is the streetlight than the person? Assume the triangles are similar.
Answer:
Length of shadow l1 = 10 ft
height of man b1 = 6 ft
Total length of bigger triangle l2 = 20 + 10 = 30 ft
l1/l2 = b1/b2
10/30 = 6/b2
b2 = 180/10
b2 = 18 ft
The ratio of the height of streetlight and man is: 18/6 = 3
Hence, the streetlight is 3 times taller than that person.
Question 17.
GEOMETRY
Use a ruler to draw two different isosceles triangles similar to the one shown. Measure the heights of each triangle.
a. Are the ratios of the corresponding heights equivalent to the ratios of the corresponding side lengths?
Answer:
b1/b2 = h1/h2
6/3 = 4/2 = 2
Hence the ratio of corresponding heights is equivalent to the ratio of corresponding side lengths.
b. Do you think this is true for all similar triangles? Explain.
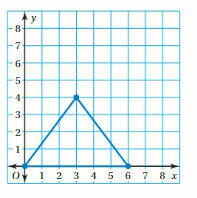
Answer:
Yes, this will be true for all the similar triangles because the heights of the two similar triangles are multiplied by the same amount as the sides.
Question 18.
CRITICAL THINKING
Given △ABC ∼ △DEF and △DEF ∼ △JKL, is △ABC ∼ △JKL? Justify your answer.
Answer:
When △ABC is similar to △DEF and △DEF is similar to △JKL, then △ABC is similar to △JKL.
Lesson 2.7 Perimeters and Areas of Similar Figures
EXPLORATION 1
Work with a partner. Draw a rectangle in the coordinate plane.
a. Dilate your rectangle using each indicated scale factor k. Then complete the table for the perimeter P of each rectangle. Describe the pattern.

b. Compare the ratios of the perimeters to the ratios of the corresponding side lengths. What do you notice?
c. Repeat part(a) to complete the table for the area A of each rectangle. Describe the pattern.
d. Compare the ratios of the areas to the ratios of the corresponding side lengths. What do you notice?

e. The rectangles shown are similar. You know the perimeter and the area of the red rectangle and a pair of corresponding side lengths. How can you find the perimeter of the blue rectangle? the area of the blue rectangle?
2.7 Lesson
Try It
Question 1.
The height of Figure A is 9 feet. The height of a similar Figure B is 15 feet. What is the value of the ratio of the perimeter of A to the perimeter of B?
Answer: The ratio of the perimeter of A to B is 3/5
Explanation:
We know that when two figures are similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of figure A/Perimeter of figure B = Height of figure A/Height of figure B
Perimeter of figure A/Perimeter of figure B = 9/15 = 3/5
Thus the ratio of the perimeter of A to B is 3/5
Try It
Question 2.
The base of Triangle P is 8 meters. The base of a similar Triangle Q is 7 meters. What is the value of the ratio of the area of P to the area of Q?
Answer:
We know that when two figures are similar then the value of the ratio of their area is equal to the square of the value of the ratio of their corresponding side lengths.
The base of Triangle P is 8 meters. The base of a similar Triangle Q is 7 meters.
b1 = 8 m
b2 = 7 m
Area of triangle P/Area of triangle Q = base of triangle P/base of triangle Q
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
COMPARING PERIMETERS OF SIMILAR FIGURES
Find the value of the ratio (red to blue) of the perimeters of the similar figures.
Question 3.

Answer:
We know that when two figures is similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of figure A/Perimeter of figure B = Side length of figure A/Side length of figure B
l1 = 9
l2 = 7
Perimeter of red figure/Perimeter of blue figure = Side length of red figure/Side length of blue figure
Perimeter of red figure/Perimeter of blue figure = 9/7
Thus the ratio of the perimeter of red to blue figure is 9/7
Question 4.
Answer:
We know that when two figures is similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of figure A/Perimeter of figure B = Side length of figure A/Side length of figure B
b1 = 8
b2 = 10
Perimeter of red figure/Perimeter of blue figure = base length of red figure/base length of blue figure
Perimeter of red figure/Perimeter of blue figure = 8/10 = 4/5
Thus the ratio of the perimeter of red to blue triangle is 4/5
COMPARING AREAS OF SIMILAR FIGURES
Find the value of the ratio (red to blue) of the areas of the similar figures.
Question 5.
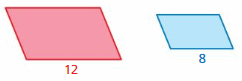
Answer:
We know that when two figures is similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of figure A/Perimeter of figure B = (Side length of figure A/Side length of figure B)²
l1 = 12
l2 = 8
Perimeter of red figure/Perimeter of blue figure = side length of red figure/side length of blue figure
Perimeter of red figure/Perimeter of blue figure = (12/8)² = (3/2)² = 9/4
Thus the ratio of the perimeter of red to blue figure is 9/4
Question 6.
Answer:
We know that when two figures is similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Area of figure A/Area of figure B = (Side length of A/Side length of B)²
l1 = 12
l2 = 8
Area of red figure/Area of blue figure = side length of red figure/side length of blue figure
Area of red figure/Area of blue figure = (4/5)² = 16/225
Thus the ratio of the perimeter of red to blue triangle is 16/225
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
Two similar triangular regions are prepared for development.

a. It costs $6 per foot to install fencing. How much does it cost to surround the forest with a fence?
Answer:
Given,
It costs $6 per foot to install fencing.
Perimeter of grassland/perimeter of forest = Height of grassland/Height of forest
h1 = 60 yards
The perimeter of grassland = 240 yards
Height of forest h2 = 45 yards
Perimeter of grassland/perimeter of forest = 60/45
240/ perimeter of forest = 60/45
the perimeter of forest = 180 yards
Convert from yards to feet
180 yards = 540 feet
Thus the cost of fencing forest = 6 × 540 = $3,240
b. The cost to prepare 1 square yard of grassland is $15 and the cost to prepare 1 square yard of forest is $25. Which region costs more to prepare? Justify your answer.
Answer:
Perimeter of grassland/perimeter of forest = (Height of grassland/Height of forest)²
Height of grassland h1 = 60 yard
Height of forest h2 = 45 yards
Area of grassland = 2400 yd²
Cost to prepare 1 sq yd of grassland = $15
Cost to prepare 1 sq yd of forest = $25
Area of forest = (2400 × 9)/16
Thus the area of forest is 1350 yd²
Cost to prepare grassland = $15 × 2400 = $36,000
Cost to prepare of forest = $25 × 1350 = $33,750
Thus the grassland will cost more to prepare.
Question 8.
DIG DEEPER!
You buy a new television with a screen similar in shape to your old television screen, but with an area four times greater. The size of a television screen is often described using the distance between opposite corners of the screen. Your old television has a 30-inch screen. What is the size of your new television screen? Explain.
Answer:
Area of ΔABC/Area of ΔDEF = (Side length of AB/Side length of DE)²
Let the area of the screen of old television be x
Let the area of the screen of new television be 4x
l1 = 30 in
Area of the screen of new television/Area of the screen of new television= (distance of the screen of new television/distance of the screen of old television)²
4x/x = (distance of the screen of new television/30)²
distance of the screen of new television = 30 × 2 = 60 inch
Hence the distance of the screen of the new television is 60 inches.
Perimeters and Areas of Similar Figures Homework & Practice 2.7
Review & Refresh
The red figure is similar to the blue figure. Describe a similarity transformation between the figures.
Question 1.
Answer:
First, dilate the red figure using the scale factor of 3 because the side lengths of the blue figure are 3 times the side length of the red figure.
Scale factor = 6/2 = 3
Now reflect the image obtained after a dilation about the y-axis because both red and blue triangle is facing each other.
Question 2.
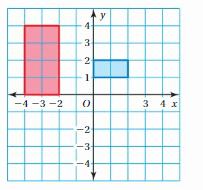
Answer:
First, dilate the red figure using the scale factor of 0.5 because the side lengths of the blue figure are 3 times the side length of the red figure.
Scale factor = 2/4 = 0.5
Then rotate the image obtained after dilation in direction 90 degrees clockwise about the origin.
Find the area of the figure.
Question 3.
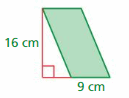
Answer:
We know that the formula for the area of trapezoid = Base × height
h = 16 cm
b = 9 cm
Area of figure = 16 × 9 = 144 sq. cm
Hence the area of the given figure is 144 sq. cm
Question 4.
Answer:
h = 5 in
b = 3 in
We know that,
A = 1/2 × b × h
A = 1/2 × 5 × 3
A = 7.5 sq. cm
Thus the area of the given figure is 7.5 sq. cm
Question 5.
Answer:
h = 5 km
b1 = 6 km
b2 = 8 km
We know that,
Area of trapezoid = 1/2 × h × (b1 + b2)
A = 1/2 × 5 × 14 = 35 sq. km
Hence the area of the trapezoid is 35 sq. km
Concepts, Skills, &Problem Solving
COMPARING SIMILAR FIGURES
Dilate the figure using the indicated scale factor k. What is the value of the ratio (new to original) of the perimeters? the areas? (See Exploration 1, p. 83.)
Question 6.
a triangle with vertices (0, 0), (0, 2), and (2, 0); k = 3
Answer:
When the points of a given figure are dilated we simply multiply each x-coordinate and y-coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
where a is the scale factor
Given a triangle with vertices (0, 0), (0, 2), and (2, 0); k = 3
A(0, 0) = A'(0 . 3, 0 . 3) = A'(0, 0)
B(0, 2) = B'(0 . 3, 2 . 3) = B'(0, 6)
C(2, 0) = C'(2 . 3, 0 . 3) = C'(6, 0)
The coordinates of the image are A'(0, 0), B'(0, 6), C'(6, 0)
AB = √(2 – 0)² – (0 – 0)² = 2
A’B’ = √(6 – 0)² – (0 – 0)² = 6
We know that when two figure are similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of new triangle/Perimeter of the original triangle = Distance of A’B’/Distance of AB = 6/2 = 3
Area of new triangle/Area of the original triangle = (Distance of A’B’/Distance of AB)² = (6/2)² = 3² = 9
Question 7.
a square with vertices (0, 0), (0, 4), (4, 4), and (4, 0); k = 0.5
Answer:
When the points of a given figure are dilated we simply multiply each x-coordinate and y-coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
where a is the scale factor
a square with vertices (0, 0), (0, 4), (4, 4), and (4, 0); k = 0.5
A(0, 0) = A'(0 . 0.5, 0 . 0.5) = A'(0, 0)
B(0, 4) = B'(0 . 0.5, 4 . 0.5) = B'(0, 2)
C(4, 4) = C'(4 . 0.5, 4 . 0.5) = C'(2, 2)
D(4, 0) = D'(4 . 0.5, 0 . 0.5) = D'(2, 0)
Coordinates of the image are A'(0, 0), B'(0, 2), C'(2, 2), D'(2, 0)
AB = √(4 – 0)² + (0 – 0)² = 4
A’B’ = √(2 – 0)² + (0 – 0)² = 2
We know that when two figure are similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of new square/Perimeter of the original square = Distance of A’B’/Distance of AB = 2/4 = 1/2
Area of new square /Area of the original square = (Distance of A’B’/Distance of AB)² = (2/4)² = 1/4
PERIMETERS AND AREAS OF SIMILAR FIGURES
Find the values of the ratios (red to blue) of the perimeters and areas of the similar figures.
Question 8.
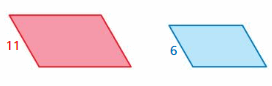
Answer:
We know that when two figure are similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of red figure/Perimeter of the blue figure = Distance of red figure/Distance of blue figure= 11/6
Area of red figure /Area of the blue figure = (Distance of red figure/Distance of blue figure)² = (11/6)² = 121/36
Question 9.
Answer:
We know that when two figure are similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of red figure/Perimeter of the blue figure = Distance of red figure/Distance of blue figure= 5/8
Area of red figure /Area of the blue figure = (Distance of red figure/Distance of blue figure)² = (5/8)² = 25/64
Question 10.
Answer:
We know that when two figure are similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of red figure/Perimeter of the blue figure = Distance of red figure/Distance of blue figure= 4/7
Area of red figure /Area of the blue figure = (Distance of red figure/Distance of blue figure)² = (4/7)² = 16/49
Question 11.
Answer:
We know that when two figure are similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of red figure/Perimeter of the blue figure = Distance of red figure/Distance of blue figure = 14/9
Area of red figure /Area of the blue figure = (Distance of red figure/Distance of blue figure)² = (14/9)² = 196/81
USING SIMILAR FIGURES
The figures are similar. Find x.
Question 12.
The ratio of the perimeters is 7 : 10.
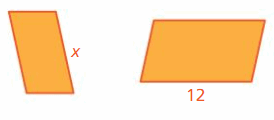
Answer:
We know that when two figure are similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of figure A/Perimeter of the figure B = Distance of figure A/Distance of figure B
7/10 = x/12
x = 84/10
x = 8.4
Thus the value of x is 8.4
Question 13.
The ratio of the perimeters is 8 : 5.
Answer:
We know that when two figure are similar then the value of the ratio of their perimeter is equal to the value of the ratio of their corresponding side lengths.
Perimeter of figure A/Perimeter of the figure B = Distance of figure A/Distance of figure B
8/5 = x/16
x = 25.6
Thus the value of x is 25.6
Question 14.
COMPARING AREAS
The playing surfaces of two foosball tables are similar. The ratio of the corresponding side lengths is 10:7. What is the ratio of the areas?
Answer:
Area of figure A /Area of figure B = (Distance of figure A/Distance of figure B)²
Area of figure A /Area of figure B = (10/7)²
Area of figure A /Area of figure B = 100/49
Hence, the ratio of their areas is 100/49
Question 15.
CRITICAL THINKING
The ratio of the side length of Square A to the side length of Square B is 4:9. The side length of Square A is 12 yards. What is the perimeter of Square B?
Answer:
Given,
The ratio of the side length of Square A to the side length of Square B is 4/9.
The side length of Square A is 12 yards.
side length of Square A/side length of Square B = 4/9
12 /side length of Square B = 4/9
side length of Square B = 27 yards
We know that,
The perimeter of the square is = 4s
The perimeter of the square B = 4 × 27 = 108 yards
Question 16.
MODELING REAL LIFE
The cost of the piece of fabric shown is $1.31. What would you expect to pay for a similar piece of fabric that is 18 inches by 42 inches?
Answer:
Given,
l = 21 in
w = 9 in
Area of the rectangle = l × w
A = 21 × 9 = 189 sq. in
The cost of the piece of fabric shown is $1.31
The cost of 1 sq. in of fabric = 1.31/189
l = 18 in
b = 42 in
Area of new fabric = 18 × 42 = 756 sq. in
Given the cost of new fabric = 1.31/189 × 756 = $5.24
Hence the cost of the new fabric is $5.24
Question 17.
PROBLEM SOLVING
A scale model of a merry-go-round and the actual merry-go-round are similar.
a. How many times greater is the base area of the actual merry-go-round than the base area of the scale model? Explain.
Answer:
Radius of model merry go round = 6 in
Radius of actual merry go round = 10 ft = 120 in
Area of base of actual merry/Area of base of model merry = (Radius of actual merry/Radius of model merry)²
Area of base of actual merry/Area of base of model merry = (120/6)² = 400
b. What is the base area of the actual merry-go-round in square feet?
Answer:
The radius of model merry go round = 6 in
Radius of actual merry go round = 10 ft = 120 in
Area of base of actual merry = 450 sq. in
Area of base of actual merry/Area of base of model merry = (Radius of actual merry/Radius of model merry)²
Area of base of actual merry/450 = (120/6)² = 400
Area of base of actual merry = 400 × 450 = 180000 sq. in = 1250 ft²
Question 18.
STRUCTURE
The circumference of Circle K is π. The circumference of Circle L is 4π. What is the value of the ratio of their circumferences? of their radii? of their areas?
Answer:
Given,
The circumference of Circle K is π
The circumference of Circle L is 4π.
circumference of Circle = 2πr
2πr = π
The radius of circle K r1 = 1/2
2πr = 4π
The radius of circle K r2 = 2
The ratio of their circumference = π/4π = 1/4
The ratio of radius of both circle = 1/4
The ratio of their area = π(r1)²/π(r2)² = 1/16
Question 19.
GEOMETRY
A triangle with an area of 10 square meters has a base of 4 meters. A similar triangle has an area of 90 square meters. What is the height of the larger triangle?
Answer:
Given,
A triangle with an area of 10 square meters has a base of 4 meters.
A similar triangle has an area of 90 square meters.
Area of the triangle = bh/2
h = 2a/b
h = (2 × 10)/4
h = 5 meters
Area of larger triangle/Area of smaller triangle = (height of larger triangle/height of smaller triangle)²
90/10 = (height of larger triangle/5)²
3 = (height of larger triangle/5)
Thus the height of larger triangle = 3 × 5 = 15 meters
Question 20.
PROBLEM SOLVING
You need two bottles of fertilizer to treat the flower garden shown. How many bottles do you need to treat a similar garden with a perimeter of 105 feet?

Answer:
The sides of the above figure are 4ft, 15 ft, 18 ft, 5 ft
Perimeter = 4ft + 15 ft + 18 ft + 5 ft = 42 ft
Number of bottle of fertilizer used in the above garden = 2
Number of bottle of fertilizer used in 1 ft = 2/42
Fertilizer used for 105 ft = 2/42 × 105 = 5
Thus 5 bottles will be used for 105 feet
Question 21.
REPEATED REASONING
Three square mirrors are used for a light reflection experiment. The ratio of the side length of Mirror A to the side length of Mirror B is 5 : 6. The ratio of the area of Mirror B to the area of Mirror C is 16 : 25. The perimeter of Mirror C is 280 centimeters. What is the area of Mirror A? Justify your answer.
Answer:
Given,
Three square mirrors are used for a light reflection experiment.
The ratio of the side length of Mirror A to the side length of Mirror B is 5 : 6 = 5/6
The ratio of the area of Mirror B to the area of Mirror C is 16 : 25 = 16/25
The perimeter of Mirror C is 280 centimeters
Side length of mirror C = Perimeter/4 = 280/4 = 70 cm
(Side length of mirror B/Side length of mirror C)² = Area of mirror A/Area of mirror B
(Side length of mirror B/Side length of mirror C)² = 16/25
(Side length of mirror B/Side length of mirror C) = 4/5
The side length of mirror B = 4/5 × Side length of mirror C
Side length of mirror B = 4/5 × 70 = 56 cm
A = s × s
A = 56 cm × 56 cm = 3136 sq. cm
Area of mirror A/Area of mirror B = (Side length of mirror A/Side length of mirror B)²
Area of mirror A/3136 = (5/6)²
Area of mirror A = 25/36 × 3136
Area of mirror A = 2177.7 sq. cm
Transformations Connecting Concepts
2 Connecting Concepts
Using the Problem-Solving Plan
Question 1.
A scale drawing of a helipad uses a scale of 1 ft : 20 ft. The scale drawing has an area of 6.25 square feet. What is the area of the actual helipad?
Understand the problem.
You know the scale of the drawing and the area of the helipad in the drawing. You are asked to find the area of the actual helipad.
Make a plan.
A scale drawing is similar to the actual object. So, use the scale 1 ft : 20 ft and the ratio 6.25 ft2 : A ft2 to write and solve a proportion that represents the area A of the actual helipad.
Solve and Check.
Use the plan to solve the problem. Then check your solution.

Answer: 125 sq. ft
Question 2.
The locations of three cargo ships are shown in the coordinate plane. Each ship travels at the same speed in the same direction. After 1 hour, the x- and y-coordinates of Ship A increase 80%. Use a translation to describe the change in the locations of the ships. Then find the new coordinates of each ship.

Question 3.
All circles are similar. A circle with a radius of 2 inches is dilated, resulting in a circle with a circumference of 22π inches. What is the scale factor? Justify your answer.
Answer:
Given,
A circle with a radius of 2 inches is dilated, resulting in a circle with a circumference of 22π inches.
C = 2π . r
22π = 2π . 2
p = 2π . 2
Thus the scale factor is 2.
Performance Task
Master Puppeteer
At the beginning of this chapter, you watched a STEAM Video called “Shadow Puppets.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Transformations Connecting Concepts
2 Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Graphic Organizers
You can use a Summary Triangle to explain a concept. Here is an example of Summary Triangle for translating a figure.
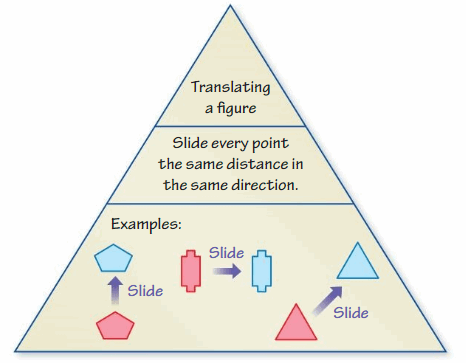
Choose and complete a graphic organizer to help you study the concept.
- reflecting a figure
- rotating a figure
- congruent figures
- dilating a figure
- similar figures
- perimeters of similar figures
- areas of similar figures

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

2.1 Translations (pp. 43–48)
Tell whether the blue figure is a translation of the red figure.
Question 1.
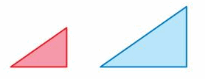
Answer: No
Explanation:
The answer is no because in the case of translation the size of the figure does not change, only the position of the figure changes. But here the size of the blue figure is larger as compared to the red figure so this is not the translation. Here the blue figure is the result of the dilation of red figure.
Question 2.
Answer: Yes
Explanation:
Yes, because in the case of translation the size of the figure does not change, only the position of the figure changes. Here the size of both blue figure and the red figure is the same but there is only a change in the position of the red figure to get blue figure. Here the blue figure is the result of the translation of the red figure.
Question 3.
The vertices of a quadrilateral are W(1, 2), X(1, 4), Y(4, 4), and Z(4, 2). Draw the figure and its image after a translation 3 units left and 2 units down.
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if shift is Right and Vertical Up and the value of a and b will be negative if shift is left and vertical Down.
Given: W(1, 2), X(1, 4), Y(4, 4), and Z(4, 2) and a = -3, b = -2
W'(1+a, 2+b) = W'(1-3, 2-2) = W'(-2,0)
X'(1+a, 4+b) = X'(1-3, 4-2) = X'(-2,2)
Y'(4+a, 4+b) = Y'(4-3, 4-2) = Y'(1, 2)
Z'(4+a, 2+b) = C'(4-3, 2-2) = Z'(1,0)
Hence the coordinate of image are W'(-2,0), X'(-2,2), Y'(1, 2), Z'(1,0)
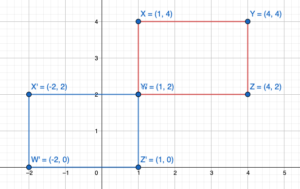
Question 4.
The vertices of a triangle are A(-1, -2), B(-2, 2), and C(-3, 0). Draw the figure and its image after a translation 5 units right and 1 unit up.
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if shift is Right and Vertical Up and the value of a and b will be negative if shift is left and vertical Down.
Given: A(-1, -2), B(-2, 2), and C(-3, 0) and a = 5, b = 1
A'(-1+a, -2+b) = A'(-1-5, -2+1) = A'(4,-1)
B'(-2+a, 2+b) = B'(-2+5, 2+1) = B'(3,3)
C'(-3+a, 0+b) = C'(-3+5, 0+1) = C'(2, 1)
Hence the coordinate of image are A'(4,-1), B'(3,3), C'(2, 1)
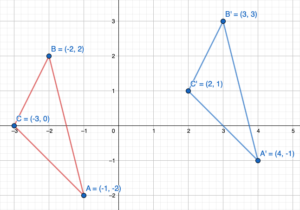
Question 5.
Your locker number is 20 and your friend’s locker number is 33. Describe the location of your friend’s locker relative to the location of your locker.

Answer:
The location of my friend’s locker is first 1 locker Down and then 3 locker Right.
Question 6.
Translate the triangle 4 units left and 1 unit down. What are the coordinates of the image?
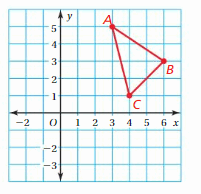
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if shift is Right and Vertical Up and the value of a and b will be negative if shift is left and vertical Down.
Given: A(3, 5), B(6, 3), and C(4, 1) and a = -4, b = -1
A'(3+a, 5+b) = A'(3-4, 5-1) = A'(-1,4)
B'(6+a, 3+b) = B'(6-4, 3-1) = B'(2,2)
C'(4+a, 1+b) = C'(4-4, 1-1) = C'(0, 0)
Hence the coordinate of image are A'(-1,4), B'(2,2), C'(0, 0)
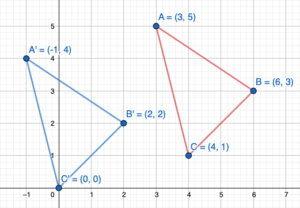
Question 7.
Describe a translation of the airplane from point A to point B.
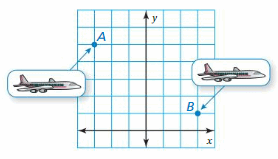
Answer:
First, move the aeroplane 6 units right from point A and then 4 units down.
2.2 Reflections (pp. 49 – 54)
Tell whether the blue figure is a reflection of the red figure.
Question 8.
Answer:
No, because in the above figure the plane of reflection is inclined at 45 degrees with the horizontal line. So, the reflected figure will be perpendicular to the original figure. But in the given figure both are facing each other. This means that the blue figure is not the reflection of red figure.
Question 9.
Answer:
The answer is no because the blue figure is not the mirror image of the red figure. The side of the red figure is not facing the side of the blue figure this means that the blue figure is not the reflection of red figure.
Question 10.
Answer:
The answer is yes because the blue figure is the mirror image of the red figure. The side of the red figure is facing the side of the blue figure this means that the blue figure is the reflection of red figure.
Draw the figure and its reflection in (a) the x-axis and (b) the y-axis. Identify the coordinates of the image.
Question 11.
A(2, 0), B(1, 5), C(4, 3)
Answer:
A(x, y) = A'(x, -y)
Given: A(2, 0), B(1, 5), C(4, 3)
Reflection about x-axis:
A(2, 0) = A'(2, 0)
B(1, 5) = B'(1, -5)
C(4, 3) = C'(4, -3)
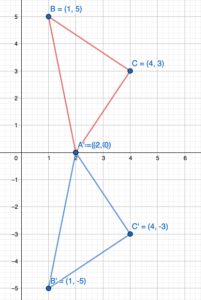
Reflection about y-axis:
A(x, y) = A'(-x, y)
A(2, 0) = A'(-2, 0)
B(1, 5) = B'(-1, 5)
C(4, 3) = C'(-4, 3)
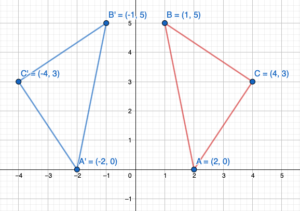
Question 12.
D(-5, -5), E(-5, 0), F(-2, -2), G(-2, -5)
Answer:
Given, D(-5, -5), E(-5, 0), F(-2, -2), G(-2, -5)
Reflection about x-axis:
A(x, y) = A'(x, -y)
D(-5, -5) = D'(-5, 5)
E(-5, 0) = E'(-5, 0)
F(-2, -2) = F'(-2, 2)
G(-2, -5) = G'(-2, 5)
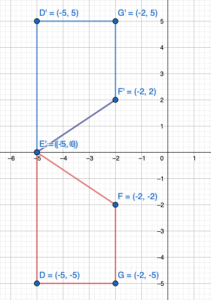
Reflection about y-axis:
A(x, y) = A'(-x, y)
D(-5, -5) = D(5, -5)
E(-5, 0) = E'(5, 0)
F(-2, -2) = F'(2, -2)
G(-2, -5) = G'(2, -5)
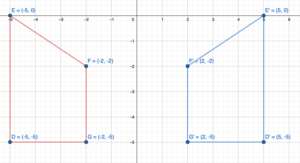
Question 13.
The vertices of a rectangle are E(-1, 1), F(-1, 3), G(-5, 3), and H(-5, 1). Find the coordinates of the figure after reflecting in the x-axis, and then translating 3 units right.
Answer:
We know that when a point is reflected about x-axis then y-coordinate becomes the opposite.
A(x, y) = A'(x, -y)
The vertices of a rectangle are E(-1, 1), F(-1, 3), G(-5, 3), and H(-5, 1).
Reflection about x-axis:
E(-1, 1) = E'(-1, -1)
F(-1, 3) = F'(-1, -3)
G(-5, 3) = G'(-5, 3)
H(-5, 1) = H'(-5, 1)
Thus the coordinates of the image are E'(-1, -1), F'(-1, -3), G'(-5, 3), H'(-5, 1)
Now translating the image 3 units Right.
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if shift is Right and Vertical Up and the value of a and b will be negative if shift is left and vertical Down.
Given: E'(-1, -1), F'(-1, -3), G'(-5, 3), H'(-5, 1) a = 3, b = 0
E”(-1 + a, -1 + b) = E”(-1 + 3, -1 + 0) = E”(2, -1)
F”(-1 + a, -3 + b) = F”(-1 + 3, -3 + 0) = F”(2, -3)
G”(-5 + a, 3 + b) = G”(-5 + 3, 3 + 0) = G”(-2, 3)
H”(-5 + a, 1 + b) = H”(-5 + 3, 1 + 0) = H”(-2, 1)
Thus the coordinates of the image are E”(2, -1), F”(2, -3), G”(-2, 3), H”(-2, 1)
The coordinates of a point and its image after a reflection are given. Identify the line of reflection.
Question 14.
(-1, -3) → (1, -3)
Answer:
Given,
(-1, -3) → (1, -3)
We can see that the y-coordinate of both points and its image are the same but the x-coordinate of the image is the opposite of its points.
Hence, Y-axis is the line of reflection.
Question 15.
(2, 1) → (2, -1)
Answer:
Given,
(2, 1) → (2, -1)
We can see that the x-coordinate of both points and its image are the same but the y-coordinate of the image is the opposite of its points.
Hence, X-axis is the line of reflection.
Question 16.
You perform an experiment involving angles of refraction with a laser pen. You point a laser pen from point L at a mirror along the red path and the image is a reflection in the y-axis.
a. Does the light reach a cat at point C? Explain.
Answer:
Yes, the light will reach at point C.
Because the coordinate of point L is (4, 3) and the coordinate of point C is (-4, 3) and it is given problems that laser is reflected about the y-axis.
So when point L(4, 3) is reflected about the y-axis its x-coordinates become opposite and y-coordinates remain the same.
So when point L(4, 3) is reflected about the y-axis its image will be point C(-4, -3)
b. You bounce the light off the mirror so its path is a reflection. What line of reflection is needed for the light to reach the cat?
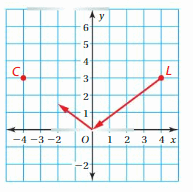
Answer: The line of reflection will be y-axis.
2.3 Rotations (pp. 55–62)
Tell whether the blue figure is a rotation of the red figure about the origin. If so, give the angle and the direction of rotation.
Question 17.
Answer:
The answer is no because the blue figure is the mirror image of the red figure. The blue figure is the result of the reflection of red figure about the y-axis. Also, both red and blue figure are facing each other with the y-axis in the center of both which remains that it is not the case of rotation.
Question 18.
Answer:
The answer is yes, because the red figure is in the 1st quadrant and the blue figure in third quadrant. Also, both blue and red figure are facing each other in opposite directions which blue figure is the result of the rotation of red figure.
When red figure is rotated 180 degrees counterclockwise it will result in a blue figure.
The vertices of a triangle are A(-4, 2), B(-2, 2), and (-3, 4). Rotate the triangle as described. Find the coordinates of the image.
Question 19.
180° about the origin
Answer:
We know that when a point is rotated 180 degrees about origin then both x coordinate and y coordinate becomes opposite.
A(x, y) = A'(-x, -y)
Given points: A(-4, 2), B(-2, 2), and C(-3, 4)
Rotated 180 degrees about origin:
A(-4, 2) = A'(4, -2)
B(-2, 2) = B'(2, -2)
C(-3, 4) = C'(3, -4)
The coordinate of the image are A'(4, -2), B'(2, -2), C'(3, -4)
Question 20.
270° clockwise about the origin
Answer:
We know that when a point is rotated 90 degrees counterclockwise about origin then both x coordinate and y coordinate becomes opposite.
P(x, y) = P'(-y, x)
Given points: A(-4, 2), B(-2, 2), and C(-3, 4)
Rotating 270 degrees clockwise about the origin:
A(-4, 2) = A'(-2, -4)
B(-2, 2) = B'(-2, -2)
C(-3, 4) = C'(-4, -3)
The coordinate of the image are A'(-2, -4), B'(-2, -2), C'(-4, -3)
Question 21.
A bicycle wheel is represented in a coordinate plane with the center of the wheel at the origin. Reflectors are placed on the bicycle wheel at points (7, 4) and (-5, -6). After a bike ride, the reflectors have rotated 90° counterclockwise about the origin. What are the locations of the reflectors at the end of the bike ride?
Answer:
We know that when a point is rotated 90 degrees counterclockwise about origin then both x coordinate and y coordinate becomes opposite.
P(x, y) = P'(-y, x)
Reflectors are placed on the bicycle wheel at points (7, 4) and (-5, -6)
A(7, 4) = A'(-4, 7)
B(-5, -6) = B'(6, -5)
Hence the new coordinate of the reflector are A'(-4, 7), B'(6, -5)
2.4 Congruent Figures (pp. 63–68)
Identify any congruent figures in the coordinate plane.
Question 22.
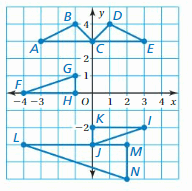
Answer:
AB = ED
BC = DC
CA = CE
∠A = ∠E
∠B = ∠D
∠C = ∠C
When we see both triangles ABC and EDC closely we observe that both the triangles are the mirror images of each other with the y-axis as the line of reflection. So all the corresponding sides are equal and also all the corresponding angles, this means that both the triangle are congruent.
Hence ΔABC is congruent to ΔEDC
GH = JK
HF = KI
FG = IJ
∠G = ∠J
∠H = ∠K
∠F = ∠I
So we can see that all the corresponding sides are equal and also all the corresponding angles. this means that both the triangles are congruent.
Hence ΔGHF is congruent to ΔJKI
Question 23.
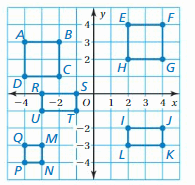
Answer:
When we observe square ABCD and square EFGH we can see that
AB = EF
BC = FG
CD = GH
DA = HE
∠A = ∠E
∠B = ∠F
∠C = ∠G
∠D = ∠H
We can see that all the corresponding sides are equal and also all the corresponding angles, this means that both are congruent.
RS = IJ
ST = JK
TU = KL
UR = LI
∠R = ∠I
∠S = ∠J
∠T = ∠K
∠L = ∠U
Hence rectangle RSTU is congruent to rectangle IJKL
The red figure is congruent to the blue figure. Describe a sequence of rigid motions between the figures.
Question 24.
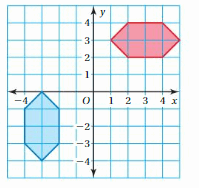
Answer:
First, rotate the blue figure 90° clockwise because the blue figure is in a vertical position but the red figure is in the horizontal position.
Translate the image 5 units right because the first image formed after the rotation will in the second quadrant but the red figure in the first quadrant.
Question 25.
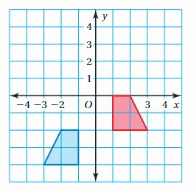
Answer:
First, reflect the blue figure about the y-axis because both red and blue figure is facing each other and they are the mirror image of each other.
Then translate the image 2 units up because the first image formed after reflection will be at the same distance from the x-axis but the red figure is touchung the x-axis.
Question 26.
The figures are congruent. Name the corresponding angles and the corresponding sides.
Answer:
Corresponding sides are
AB = KL
BC = LM
CA = MK
Corresponding angles
∠A = ∠K
∠B = ∠L
∠C = ∠M
Question 27.
Trapezoids EFGH and QRST are congruent.
a. What is the length of side QR ?
Answer:
Length of side:
QR = EF = 3 feet
b. Which angle in QRST corresponds to ∠H?
Answer:
The angle that corresponds to ∠H is ∠T
c. What is the perimeter of QRST ?
Answer:
Perimeter of QSRT = QR + RS + ST + TQ
= EF + FG + GH + HE
= 3 + 5 + 4 + 8
= 20 ft
2.5 Dilations (pp. 69–76)
Tell whether the blue figure is a dilation of the red figure.
Question 28.
Answer:
The answer is no because dilation the size of the image either increases or decreases that depend on the type of dilation. We can see that both the red and blue figure are of the same size which means that the blue figure is not dilation of the red figure.
Question 29.
Answer:
The answer is yes because both red and blue figures are of the same shape and all the corresponding angles are equal but the blue figure is larger than the red figure. And in dilation, the size of the image is either increases or decreases but the shape always remains the same. So blue figure is the result of dilation of red figure.
The vertices of a figure are given. Draw the figure and its image after a dilation with the given scale factor. Identify the type of dilation.
Question 30.
P(-3, -2), Q(-3, 0), R(0, 0); k = 4
Answer:
A(x, y) = A'(x . a, y . a)
Where a is the scaling factor
Given,
P(-3, -2), Q(-3, 0), R(0, 0); k = 4
P(-3, -2) = P'(-3 . 4, -2 . 4) = P'(-12, -8)
Q(-3, 0) = Q'(-3 . 4, 0 . 4) = Q'(-12, 0)
R(0, 0) = R'(0 . 4, 0 . 4) = R'(0, 0)
Thus the coordinates of the image: P'(-12, -8), Q'(-12, 0), R'(0, 0)
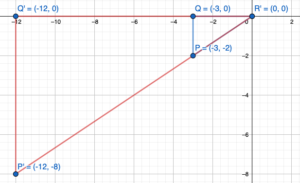
Question 31.
B(3, 3), C(3, 6), D(6, 6), E(6, 3); k = \(\frac{1}{3}\)
Answer:
A(x, y) = A'(x . a, y . a)
Where a is the scaling factor
Given,
B(3, 3), C(3, 6), D(6, 6), E(6, 3); k = \(\frac{1}{3}\)
B(3, 3) = B'(3 . \(\frac{1}{3}\), 3 . \(\frac{1}{3}\)) = B'(1, 1)
C(3, 6) = C'(3 . \(\frac{1}{3}\), 6 . \(\frac{1}{3}\)) = C'(1, 2)
D(6, 6) = D'(6 . \(\frac{1}{3}\), 6 . \(\frac{1}{3}\)) = D'(2, 2)
E(6, 3) = E'(6 . \(\frac{1}{3}\), 3 . \(\frac{1}{3}\)) = E'(2, 1)
Thus the coordinates of the image: B'(1, 1), C'(1, 2), D'(2, 2), E'(2, 1)
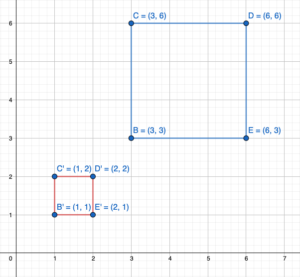
Question 32.
The blue figure is a dilation of the red figure. Identify the type of dilation and find the scale factor.
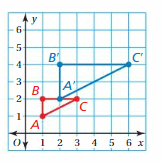
Answer:
AB = 1 unit
A’B’ = 2 units
scale factor = size of image figure/size of actual figure
scale factor = 2/1 = 2
We can see from the above figure that the size of the image figure are larger as compared to the size of the original image so it is the Enlargement dilation.
Question 33.
The vertices of a rectangle are Q(-6, 2), R(6, 2), S(6, -4), and T(-6, -4). Dilate the rectangle with respect to the origin using a scale factor of \(\frac{3}{2}\). Then translate it 5 units right and 1 unit down. What are the coordinates of the image?
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given points of the rectangle: Q(-6, 2), R(6, 2), S(6, -4), and T(-6, -4), scale factor = \(\frac{3}{2}\)
Q(-6, 2) = Q'(-6 . \(\frac{3}{2}\), 2 . \(\frac{3}{2}\)) = Q'(-9, 3)
R(6, 2) = R'(6 . \(\frac{3}{2}\), 2 . \(\frac{3}{2}\)) = R'(9, 3)
S(6, -4) = S'(6 . \(\frac{3}{2}\), -4 . \(\frac{3}{2}\)) = S'(9, 6)
T(-6, -4) = T'(-6 . \(\frac{3}{2}\), -4 . \(\frac{3}{2}\)) = T'(-9, -6)
Thus the coordinates of the image: Q'(-9, 3), R'(9, 3), S'(9, 6), T'(-9, -6)
Q'(-9, 3), R'(9, 3), S'(9, 6), T'(-9, -6) a = 5, b = -1
Q”(-9 + a, 3 + b) = Q”(-9 + 5, 3 – 1) = Q”(-4, 2)
R”(9 + a, 3 + b) = R”(9 + 5, 3 – 1) = R”(14, 2)
S”(9 + a, -6 + b) = S”(9 + 5, -6 – 1) = S”(14, -7)
T”(-9 + a, -6 + b) = T”(-9 + 5, -6 – 1) = T”(-4, -7)
Thus the coordinates of the image: Q”(-4, 2), R”(14, 2), S”(14, -7), T”(-4, -7)
2.6 Similar Figures
Question 34.
Determine whether the two figures are similar. Explain your reasoning.
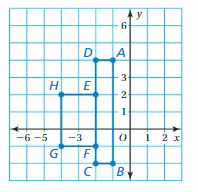
Answer:
No, the above two figures are not similar.
Question 35.
Draw figures with the given vertices in a coordinate plane. Which figures are similar? Explain your reasoning.
Triangle A: (-4, 4), (-2, 4), (-2, 0)
Triangle B: (-2, 2), (-1, 2), (-1, 0)
Triangle C: (6, 6), (3, 6), (3, 0)
Answer:
Triangle A: (-4, 4), (-2, 4), (-2, 0)
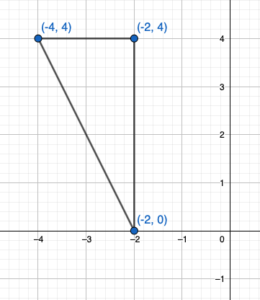
Triangle B: (-2, 2), (-1, 2), (-1, 0)
Triangle C: (6, 6), (3, 6), (3, 0)
The figures are similar. Find x.
Question 36.
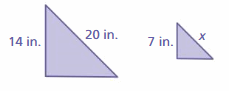
Answer:
Ratio of sides of larger triangle = Ratio of sides of smaller triangle
20/14 = x/7
x = 10
Thus the value of x is 7 inches.
Question 37.
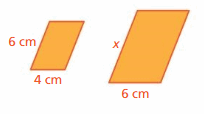
Answer:
Ratio of sides of larger parallelogram= Ratio of sides of smaller parallelogram
x/6 = 6/4
x = 9
Thus the value of x is 9 cm
2.7 Perimeters and Areas of Similar Figures (pp. 83-88)
Find the values of the ratios (red to blue) of the perimeters and areas of the similar figures.
Question 38.
Answer:
Perimeter of figure A/Perimeter of figure B = Side length of figure A/Side length of figure B
Perimeter of red figure/Perimeter of blue figure = 6/8 = 3/4
Hence the ratio of perimeter of red triangle to blue is 3/4
Area of figure A/Area of figure B = (Side length of A/Side length of B)²
Area of red figure/Area of blue figure = (6/8)² = 9/16
Thus the ratio of the perimeter of the red to the blue triangle is 9/16
Question 39.

Answer:
Perimeter of figure A/Perimeter of figure B = Side length of figure A/Side length of figure B
Perimeter of red figure/Perimeter of blue figure = 28/16 = 7/4
Hence the ratio of the perimeter of red rectangle to blue is 7/4
Area of figure A/Area of figure B = (Side length of A/Side length of B)²
Area of red figure/Area of blue figure = (28/16)² = 49/16
Thus the ratio of the perimeter of the red to the blue rectangle is 49/16
The figures are similar. Find x.
Question 40.
The ratio of the perimeters is 5 :7.
Answer:
5/7 = 12/x
x =(12 × 7)/5
x = 16.8 cm
Thus the value of x is 16.8 cm
Question 41.
The ratio of the perimeters is 6 : 5.
Answer:
6/5 = x/6
x = 36/5
x = 7.2
Thus the value of x is 7.2
Question 42.
Two photos are similar. The ratio of the corresponding side lengths is 3 : 4. What is the ratio of the areas?
Answer:
Area of photo A/Area of photo B = (Side length of photo A/Side length of photo B)²
Area of photo A/Area of photo B = (3/4)² = 9/16
Thus the ratio of the area of two photos is 9/16
Question 43.
The ratio of side lengths of Square A to Square B is 2 : 3. The perimeter of Square A is 16 inches. What is the area of Square B?
Answer:
Given,
The ratio of side lengths of Square A to Square B is 2 : 3.
The perimeter of Square A is 16 inches.
Perimeter of Square A/Perimeter of Square B = Side length of Square A/Side length of Square B
The perimeter of Square B = (16 × 3)/2
The perimeter of Square B = 24 inches
Side length of square B = Perimeter/4 = 24/4 = 6 inch
Area of square B = s × s = 6 × 6 = 36 sq. in
Question 44.
The TV screen is similar to the computer screen. What is the area of the TV screen?

Answer:
Area of computer screen = 108 sq. in
The side length of the computer screen = 12 in
The side length of the TV screen = 20 in
Area of TV screen = (25 × 108)/9
Area of TV screen = 300 sq. in
Hence the area of the TV screen is 300 sq. in
Transformations Practice Test
2 Practice Test
Triangles ABC and DEF are congruent.
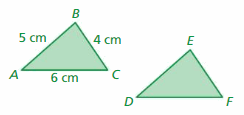
Question 1.
Which angle of DEF corresponds to ∠C ?
Answer:
Corresponding sides
Side AB = Side DE
Side BC = Side EF
Side CA = Side ED
Corresponding angles
∠A = ∠D
∠B = ∠E
∠C = ∠F
Thus the angle correspond to ∠C is ∠F
Question 2.
What is the perimeter of DEF ?
Answer:
Corresponding sides
Side AB = Side DE
Side BC = Side EF
Side CA = Side ED
Corresponding angles
∠A = ∠D
∠B = ∠E
∠C = ∠F
Perimeter of DEF = DE + EF + FD
= AB + BC + CA
= 5 + 4 + 6
= 15 cm
Thus the perimeter of the ΔDEF is 15 cm
Tell whether the blue figure is a translation, reflection, rotation, or dilation of the red figure.
Question 3.

Answer: The scale factor of a dilation is greater than 1 because the shape of the blue figure is larger than the red figure.
Question 4.
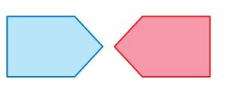
Answer:
The blue figure is the reflection of the red figure. Because the blue figure is the mirror image of red figure. Also, the shape and size of both red and blue figures are the same.
Question 5.
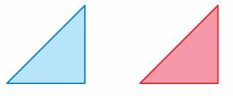
Answer:
The blue figure is the translation of the red figure. Because the shape and size of both red and blue figures are the same. And both the figure is not facing to each other. This means that the blue figure is the result of the translation of the red figure.
Question 6.
Answer:
The blue figure is the result of the rotation of the red figure. Because the shape and size of both the red and blue figure are the same but the figure is horizontal and the blue figure is vertical. This means that the blue figure is the result of the rotation of the term figure.
The vertices of a triangle are A(2, 5), B(1, 2), and C(3, 1). Find the coordinates of the image after the transformations given.
Question 7.
Reflect in the y-axis.
Answer:
A(x, y) = A'(-x, y)
A(2, 5), B(1, 2), C(3, 1)
Reflection about the y-axis:
A(2, 5) = A'(-2, 5)
B(1, 2) = B'(-1, 2)
C(3, 1) = C'(-3, 1)
Thus the coordinates of the image: A'(-2, 5), B'(-1, 2), C'(-3, 1)
Question 8.
Rotate 90° clockwise about the origin.
Answer:
A(x, y) = A'(x, -y)
Given, A(2, 5), B(1, 2), C(3, 1)
A(2, 5) = A'(2, -5)
B(1, 2) = B'(1, -2)
C(3, 1) = C'(3, -1)
Thus the coordinates of the image: A'(2, -5), B'(1, -2), C'(3, -1)
Question 9.
Reflect in the x-axis, and then rotate 90° counterclockwise about the origin.
Answer:
A(x, y) = A'(x, -y)
Given, A(2, 5), B(1, 2), C(3, 1)
A(2, 5) = A'(2, -5)
B(1, 2) = B'(1, -2)
C(3, 1) = C'(3, -1)
Thus the coordinates of the image: A'(2, -5), B'(1, -2), C'(3, -1)
A'(2, -5) = A”(2, 5)
B'(1, -2) = B”(1, 2)
C'(3, -1) = C”(3, 1)
Thus the coordinates of the image: A”(2, 5), B”(1, 2), C”(3, 1)
Question 10.
Dilate with respect to the origin using a scale factor of 2. Then translate 2 units left and 1 unit up.
Answer:
When the points of given figure are dilated we simply multiply each x and y coordinate by the given scale factor.
P(x, y) = P'(x . a, y . a)
Given points of the triangle: A(2, 5), B(1, 2), C(3, 1) and scale factor = 2
Dilating the figure by scale factor of 2
A (2, 5) = A'(2 . 2, 5 . 2) = A'(4, 10)
B (1, 2) = B'(1 . 2, 2 . 2) = B'(2, 4)
C (3, 1) = C'(3 . 2, 1 . 2) = C'(6, 2)
Hence the coordinates of the image are A'(4, 10), B'(2, 4), C'(6, 2)
Now translating image 2 unit left and 1 unit up.
Given: A'(4, 10), B'(2, 4), C'(6, 2) a = -2, b = 1
A”(4 + a, 10 + b) = A”(4 – 2, 10 + 1) = A”(2, 11)
B”(2 + a, 4 + b) = B”(2 – 2, 4 + 1) = B”(0, 5)
C”(6 + a, 2 + b) = C”(6 – 2, 2 + 1) = C”(4, 3)
Hence the coordinates of the image are A”(2, 11), B”(0, 5), C”(4, 3)
Question 11.
In a coordinate plane, draw Rectangle A: (-4, 4), (0, 4), (0, 2), (-4, 2); Rectangle B: (-2, 2), (0, 2), (0, 1), (-2, 1); and Rectangle C:(-6, 6), (0, 6), (0, 3), (-6, 3). Which figures are similar? Explain your reasoning.
Answer:
Rectangle A: (-4, 4), (0, 4), (0, 2), (-4, 2)
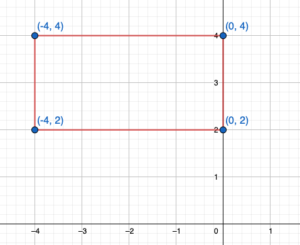
Rectangle B: (-2, 2), (0, 2), (0, 1), (-2, 1)
Rectangle C:(-6, 6), (0, 6), (0, 3), (-6, 3)
Question 12.
Translate a point (x, y) 3 units left and 5 units up. Then translate the image 5 units right and 2 units up. What are the coordinates of the point after the translations?
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to the y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if the shift is Right and Vertical Up and the value of a and b will be negative if the shift is left and vertical Down.
Given: A(x,y) and a = -3, b = 5
A'(x+a, y+b) = A'(x – 3, y + 5)
Now translating image 5 units right and 2 units up.
Image after first translation: A'(x – 3, y + 5) and a = 5, b = 2
A”(x – 3 + a, y + 5 + b) = A”(x – 3 + 5, y + 5 + 2) = A”(x + 2, y + 7)
Thus the final image will be A”(x + 2, y + 7)
Question 13.
The two figures are similar.
(a) Find the value of x.
Answer:
Ratio of sides of red figure = Ratio of sides of blue figure
x/14 = 10/8
x = (10 × 14)/8
x = 17.5
(b) Find the values of the ratios (red to blue) of the perimeters and of the areas.
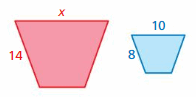
Answer:
Perimeter of red figure/Perimeter of blue figure = Side length of red figure/Side length of blue figure
Perimeter of red figure/Perimeter of blue figure = 14/8 = 7/4
Thus the ratio of the perimeter of red to blue figure is 7/4
Area of red figure/Area of blue figure = (side length of red figure/side length of blue figure)²
Area of red figure/Area of blue figure = (14/8)² = 49/16
Thus the ratio of the perimeter of red to blue triangle is 49/16
Question 14.
A wide-screen television measures 36 inches by 54 inches. A movie theater screen measures 42 feet by 63 feet. Are the screens similar? Explain.
Answer:
Given,
A wide-screen television measures 36/54 = 2/3
A movie theater screen measures 42/63 = 2/3
We can see that the ratio of corresponding sides of the television screen is equal to the ratio of corresponding sides of the movie theatre. So television screens and movie theatres are similar.
Question 15.
You want to use the rectangular piece of fabric shown to make a pair of curtains for your window. Name the types of congruent shapes you can make with one straight cut. Draw an example of each type.

Answer:
The types of congruent shapes that can be made with one straight cut
2 right triangles
2 rectangles
2 right trapezoid
Transformations Cumulative Practice
Cumulative Practice
Question 1.
A clockwise rotation of 90° is equivalent to a counterclockwise rotation of how many degrees?


Answer:
90° of clockwise rotation = (360 – 90)° of counterclockwise rotation
= 270° of counterclockwise rotation
Question 2.
The formula K = C + 273.15 converts temperatures from degrees Celsius C to Kelvin K. Which of the following formulas is not correct?
A. K – C = 273.
B. C = K – 273.15
C. C – K = -273.15
D. C = K + 273.15
Answer: C = K + 273.15
Question 3.
You want to solve the equation -3(x + 2) = 12x. What should you do first?
F. Subtract 2 from each side.
G. Add 3 to each side.
H. Multiply each side by -3.
I. Divide each side by -3.
Answer: I. Divide each side by -3.
Explanation:
-3(x + 2) = 12x
x + 2 = -4x
x = -4x – 2
x + 4x = -2
5x = -2
x = –\(\frac{2}{5}\)
Thus the correct answer is option I.
Question 4.
Which value of x makes the equation \(\frac{3}{4} x\) = 12 true?
A. 9
B. 11\(\frac{1}{4}\)
C. 16
D. 48
Answer: C. 16
Explanation:
\(\frac{3}{4} x\) = 12
3x = 12 × 4
3x = 48
x = \(\frac{48}{3}\)
x = 16
Thus the correct answer is option C.
Question 5.
A triangle is graphed in the coordinate plane. What are the coordinates of the image after a translation 3 units right and 2 units down?
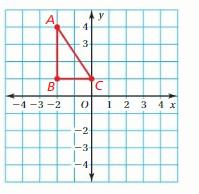
F. A'(1, 4), B'(1, 1), C'(3, 1)
G. A'(1, 2), B'(1, -1), C'(3, -1)
H. A'(-2, 2), B'(-2, -1), C'(0, -1)
I. A'(0, 1), B'(0, -2), C'(2, -2)
Answer:
We know that to translate a figure ‘a’ units horizontally and ‘b’ units vertically in the coordinate plane, ‘a’ is added to x-coordinate and ‘b’ is added to the y-coordinate of the vertices.
A(x,y) = A'(x+a, y+b)
The value a and b will be positive if the shift is Right and Vertical Up and the value of a and b will be negative if the shift is left and vertical Down.
A(-2, 4), B(-2, 1), C(0, 1) and a = 3, b = -2
A'(-2+a, 4+b) = A'(-2 + 3, 4 – 2) = A'(1, 2)
B'(-2+a, 1+b) = B'(-2 + 3, 1 – 2) = B'(1,-1)
C'(0+a, 1+b) = C'(0 + 3, 1 – 2) = C'(3, -1)
Coordinate of the image are: A'(1, 2), B'(1,-1), C'(3, -1)
Thus the correct answer is option G.
Question 6.
Your friend solved the equation in the box shown. What should your friend do to correct the error that he made?
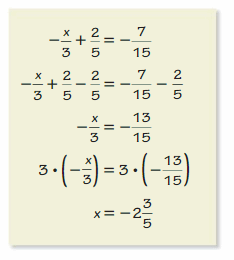
Answer:
–\(\frac{x}{3}\) + \(\frac{2}{5}\) = –\(\frac{7}{15}\)
–\(\frac{x}{3}\) = –\(\frac{13}{15}\)
x = 2\(\frac{3}{5}\)
Thus the correct answer is option C.
Question 7.
Your teacher dilates the rectangle using a scale factor of \(\frac{1}{2}\).
What is the area of the dilated rectangle in square inches?
Answer:
l = 10 in
b = 6 in
scale factor = \(\frac{1}{2}\)
New length after dilation = 10 × \(\frac{1}{2}\) = 5
New breadth after dilation = 6 × \(\frac{1}{2}\) = 3
Area of rectangle = l × b
A = 5 × 3 = 15 sq. in
The area of the dilated rectangle will be 5 in²
Question 8.
Your cousin earns $9.25 an hour at work. Last week she earned $222.00 How many hours did she work last week?
F. \(\frac{1}{24}\)
G. 22 hours
H. 24 hours
I. 212.75 hours
Answer: H. 24 hours
Explanation:
Given,
Your cousin earns $9.25 an hour at work.
Last week she earned $222.00
Total no. of working hour = total earning of week/rate of one hour
= \(\frac{222}{9.25}\)
= 24 hours
Thus the correct answer is option H.
Question 9.
Triangle EFG is a dilation of Triangle HIJ. Which proportion is not true for Triangle EFG and Triangle HIJ ?

Answer: \(\frac{EG}{HI}\) = \(\frac{FG}{IJ}\)
The correct answer is option B.
Question 10.
The red figure is congruent to the blue figure. Which of the following is a sequence of rigid motions between the figures?
F. Reflect the red triangle in the x-axis, and then translate it 3 units left.
G. Reflect the red triangle in the x-axis, and then translate it 3 units right.
H. Reflect the red triangle in the y-axis, and then translate it 3 units left.
I. Rotate the red triangle 90° clockwise about the origin.
Answer:
1. First red triangle is reflected about the x-axis because both red and blue triangles are the mirror image of each other and also the red triangle is in the 1st quadrant and the blue triangle is in 4th quadrant.
2. Then translate the image 3 unit left because the base of both red and blue triangles is not opposite to each other.
Thus the correct answer is option F.
Question 11.
Several transformations are used to create the pattern.
Part A
Describe the transformation of Triangle GLM to Triangle DGH
Answer:
Both ΔGLM and Δ DGH are of the same shape and size but their position are different so the transformation will be translated.
Part B
Describe the transformation of Triangle ALQ to Triangle GLM.
Answer:
The size of the triangle ALQ is four times the size of triangle GLM and the shape of both triangles is the same so the transformation will be dilation.
Part C
Triangle DFN is a dilation of Triangle GHM. Find the scale factor.

Answer:
The size of the triangle DFN is double the size of triangle GHM. So the scale factor of dilation will be 2.
Question 12.
A rectangle is graphed in the coordinate plane.
What are the coordinates of the image after a reflection in the y-axis?
A. J'(4, 1), K'(4, 3), L'( 1, 3), M'(-1, 1)
B. J'(-4, 1), K(-4, -3), L'(1, -3), M'(1, 1)
C. J'(1, 4), K'(3, 4), L'(3, -1), M'(1, -1)
D. J'(-4, 1), K'(-4, 3), L'(1, 3), M'(1, 1)
Answer:
We know that when a point is reflected about the y-axis then the x-coordinate becomes the opposite.
A(x, y) = A'(-x, y)
J(-4, 1), K(-4, 3), L(1, 3), M(1, 1)
Reflection about the y-axis:
J(-4, 1) = J'(4, 1)
K(-4, 3) = K'(4, 3)
L(1, 3) = L'(-1, 3)
M(1, 1) = M'(-1, 1)
Coordinate of image are: J'(4, 1), K'(4, 3), L'(-1, 3), M'(-1, 1)
Thus the correct answer is option A.
Conclusion:
I wish the information provided in the above article regarding the Big Ideas Math Grade 8 Chapter 2 Transformations Answer Key is beneficial for all middle school students. Make use of the given links and score good marks in the exams. Share this pdf with your friends and help them to overcome the difficulties in maths. And also bookmark our page to get the latest updates of all Big Ideas Math Grade 8 Answers.