Wondering how to ace up your preparation for Chapter 7 Polynomial Equations and Factoring? Then don’t be worried at all. Here comes the best & helpful guide ie., Big Ideas Math Algebra 1 Answers Chapter 7 Polynomial Equations and Factoring. By referring to this guide, you will find all Polynomial Equations and Factoring topics answers and solutions in an explanative way & understand each and every concept of polynomials and factoring so easily.
For better learnings, we have curated Big Ideas Math Book Algebra 1 Ch 7 Polynomial Equations and Factoring 7.1 to 7.8 Exercises Questions, Chapter Review, Chapter Test, Cumulative Assessment, etc. Also, check out the more Big Ideas Math Algebra 1 Answers to gain more marks in the examinations.
Big Ideas Math Book Algebra 1 Answer Key Chapter 7 Polynomial Equations and Factoring
Solving all practice questions, quizzes, and text questions provided here on Big Ideas Math Algebra 1 Answers Chapter 7 Polynomial Equations and Factoring aid in your preparation. Big Ideas math book Answers not only provides solutions to every chapter of Algebra 1 but also offering Grade K to High School Big Ideas Math Answers Solutions Common Core 2019 PDF Download.
So, download the pdf’s and start preparing math concepts covered in Common Core Edition 2019 Big Ideas Math Books and score better marks in the annual exams. To help you out in choosing the Topic-wise Ch 7 Big Ideas Math Book Algebra 1 Polynomial Equations and Factoring Exercises Answers, we have given direct links below. Click on the respective link and kickstart your learnings.
- Polynomial Equations and Factoring Maintaining Mathematical Proficiency – Page 355
- Polynomial Equations and Factoring Mathematical Practices – Page 356
- Lesson 7.1 Adding and Subtracting Polynomials – Page (357 to 364)
- Adding and Subtracting Polynomials 7.1 Exercises – Page (362 to 364)
- Lesson 7.2 Multiplying Polynomials – Page (365 to 370)
- Multiplying Polynomials 7.2 Exercises – Page (369 to 370)
- Lesson 7.3 Special Products of Polynomials – Page (371 to 376)
- Special Products of Polynomials 7.3 Exercises – Page (375 to 376)
- Lesson 7.4 Solving Polynomial Equations in Factored Form – Page (377 to 382)
- Solving Polynomial Equations in Factored Form 7.4 Exercises – Page (381 to 382)
- Polynomial Equations and Factoring Study Skills: Preparing for a Test – Page 383
- Polynomial Equations and Factoring 7.1–7.4 Quiz – Page 384
- Lesson 7.5 Factoring x2 + bx + c – Page (385 to 390)
- Factoring x2 + bx + c 7.5 Exercises – Page (389 to 390)
- Lesson 7.6 Factoring ax2 + bx + c – Page (391 to 396)
- Factoring ax2 + bx + c 7.6 Exercises – Page (395 to 396)
- Lesson 7.7 Factoring Special Products – Page (397 to 402)
- Factoring Special Products 7.7 Exercises – Page (401 to 402)
- Lesson 7.8 Factoring Polynomials Completely – Page (403 to 408)
- Factoring Polynomials Completely 7.8 Exercises – Page (407 to 408)
- Polynomial Equations and Factoring Performance Task: The View Matters – Page 409
- Polynomial Equations and Factoring Chapter Review – Page (410 to 412)
- Polynomial Equations and Factoring Chapter Test – Page 413
- Polynomial Equations and Factoring Cumulative Assessment – Page (414 to 415)
Polynomial Equations and Factoring Maintaining Mathematical Proficiency
Simplify the expression.
Question 1.
3x – 7 + 2x
Answer:
Given expression
3x – 7 + 2x
Combine the like terms
3x – 7 + 2x = 5x – 7
Question 2.
4r + 6 – 9r – 1
Answer:
Given expression
4r + 6 – 9r – 1
Combine the like terms
4r – 9r + 6 – 1 = -5r + 5 = -5(r – 1)
So, 4r + 6 – 9r – 1 = -5(r – 1)
Question 3.
-5t + 3 – t – 4 + 8t
Answer:
Given expression
-5t + 3 – t – 4 + 8t
Combine the like terms
-5t + 3 – t – 4 + 8t
= -5t – t + 8t + 3 – 4
= 2t – 1
So, -5t + 3 – t – 4 + 8t = 2t – 1
Question 4.
3(s – 1) + 5
Answer:
Given expression
3(s – 1) + 5
Combine the like terms
3(s – 1) + 5
= 3s – 3 + 5
= 3s + 2
So, 3(s – 1) + 5 = 3s + 2
Question 5.
2m – 7(3 – m)
Answer:
Given expression
2m – 7(3 – m)
Combine the like terms
= 2m – 21 + 7m
= 2m + 7m – 21
= 9m – 21
= 3(3m – 7)
So, 2m – 7(3 – m) = 3(3m – 7)
Question 6.
4(h + 6) – (h – 2)
Answer:
Given expression
4(h + 6) – (h – 2)
Combine the like terms
4(h + 6) – (h – 2)
= 4h + 24 – h + 2
= 4h – 4 + 24 + 2
= 3h + 25
So, 4(h + 6) – (h – 2) = 3h + 25.
Find the greatest common factor.
Question 7.
20, 36
Answer:
Factors of 20 = 1, 2, 4, 5, 10 and 20.
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 and 36.
The greatest common factor of 20 and 36 is 4.
Question 8.
42, 63
Answer:
Factors of 42 = 1, 2, 3, 6, 7, 14, 21, 42
Factors of 63 = 1, 3, 7, 9, 21, 63
The greatest common factor of 42 and 63 is 21.
Question 9.
54, 81
Answer:
Factors of 54 = 1, 2, 3, 6, 9, 18, 27, 54
Factors of 81 = 1, 3, 9, 27, 81
The greatest common factor of 54 and 81 is 27.
Question 10.
72, 84
Answer:
Factors of 72 = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 84 = 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
The greatest common factor of 72 and 84 is 12.
Question 11.
28, 64
Answer:
Factors of 28 = 1, 2, 4, 7, 14, 28
Factors of 64 = 1, 2, 4, 8, 16, 32, 64
The greatest common factor of 28 and 64 is 4.
Question 12.
30, 77
Answer:
Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30
Factors of 77 = 1, 7, 11, 77
The greatest common factor of 30 and 77 is 1.
Question 13.
ABSTRACT REASONING
Is it possible for two integers to have no common factors? Explain your reasoning.
Answer: No. Even if both integers are prime, they still share the common factor of 1.
Polynomial Equations and Factoring Mathematical Practices
Mathematically proficient students consider concrete models when solving a mathematics problem.
Monitoring Progress
Write the algebraic expression modeled by the algebra tiles.
Question 1.
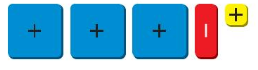
Answer:
x² + x² + x² – x² + 1
= 3x² – x² + 1
= 2x² + 1
Question 2.

Answer:
x – x² = x(1 – x)
Question 3.

Answer:
-x² – x – x
= -x² – 2x
= -x(x + 2)
Question 4.

Answer:
x + x² – 1
x² + x – 1
Question 5.
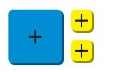
Answer:
x² + 1 + 1
= x² + 2
Question 6.

Answer:
x – 1 – 1 – 1 – 1 – 1 – 1
x – 6
Question 7.
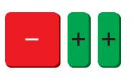
Answer:
-x² + x + x
-x² + 2x
x(-x + 2)
x(2 – x)
Question 8.

Answer:
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 9
Question 9.
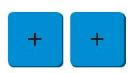
Answer:
x² + x² = 2x²
Lesson 7.1 Adding and Subtracting Polynomials
Essential Question How can you add and subtract polynomials?
EXPLORATION 1
Adding Polynomials
Work with a partner. Write the expression modeled by the algebra tiles in each step.
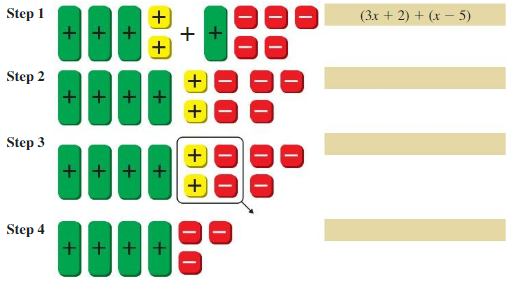
Answer:
Step 1: x + x + x + 1 + 1 + x – 1 – 1 – 1 – 1 – 1
= (3x + 2) + (x – 5)
Step 2: x + x + x + x + 1 + 1 – 1 – 1 – 1 – 1 – 1
Step 3: x + x + x + x + 1 + 1 – 1 – 1 – 1 – 1 – 1
Step 4: 4x – 3
EXPLORATION 2
Subtracting Polynomials
Work with a partner. Write the expression modeled by the algebra tiles in each step.
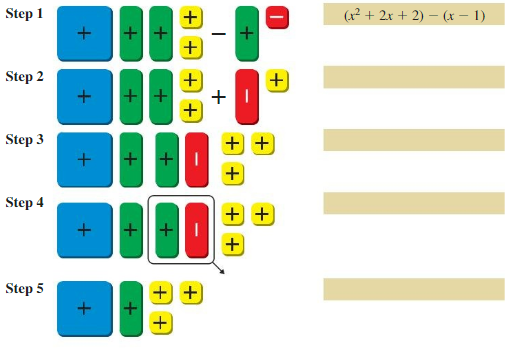
Answer:
Step 1: x² + x + x + 1 + 1 – x – 1
= (x² + 2x + 2) – (x – 1)
Step 2: x² + x + x + 1 + 1 + (-1 + 1)
x² + 2x + 2
Step 3: x² + x + x – 1 + 1 + 1 + 1
x² + 2x + 2
Step 4: x² + x + (x – x) + 1 + 1 + 1
x² + x + 3
Step 5: x² + x + 1 + 1 + 1
x² + x + 3
Communicate Your Answer
Question 3.
How can you add and subtract polynomials?

Answer:
Your first step is to change the subtraction problem to an addition problem. Then you add, just as you did in the adding polynomials lesson. Let’s take a look at an example. Once we change this problem to an addition problem, we will use the horizontal method for solving it.
Question 4.
Use your methods in Question 3 to find each sum or difference.
a. (x2 + 2x – 1) + (2x2 – 2x + 1)
b. (4x + 3) + (x – 2)
c. (x2 + 2) – (3x2 + 2x + 5)
d. (2x – 3x) – (x2 – 2x + 4)
Answer:
a. (x2 + 2x – 1) + (2x2 – 2x + 1)
Combine the like terms to add or subtract the polynomials
(x2 + 2x – 1) + (2x2 – 2x + 1)
x² + 2x² + 2x – 2x – 1 + 1
3x²
(x2 + 2x – 1) + (2x2 – 2x + 1) = 3x²
b. (4x + 3) + (x – 2)
Combine the like terms to add or subtract the polynomials
(4x + 3) + (x – 2)
4x + x + 3 – 2
5x + 1
c. (x2 + 2) – (3x2 + 2x + 5)
Combine the like terms to add or subtract the polynomials
(x2 + 2) – (3x2 + 2x + 5)
x² – 3x² – 2x + 2 – 5
-2x² – 2x – 3
-(2x² + 2x + 3)
d. (2x – 3x) – (x2 – 2x + 4)
Combine the like terms to add or subtract the polynomials
(2x – 3x) – (x2 – 2x + 4)
-x – x² + 2x – 4
-x² + x – 4
-(x² – x + 4)
Monitoring Progress
Find the degree of the monomial.
Question 1.
-3x4
Answer:
The degree of a monomial is the sum of the exponents of the variables.
-3x4 = The degree of the monomial is 4.
Question 2.
7c3d2
Answer:
7c3d2
The degree of c is 3
The degree of d is 2
The degree of the monomial = 3 + 2 = 5
Question 3.
\(\frac{5}{3}\)y
Answer:
\(\frac{5}{3}\)y
The degree of the monomial is 1.
Question 4.
-20.5
Answer:
Given monomial is -20.5
-20.5 is same as -20.5x0 since anything to the zero power is equal to 1.
Write the polynomial in standard form. Identify the degree and leading coefficient of the polynomial. Then classify the polynomial by the number of terms.
Question 5.
4 – 9z
Answer:
4 – 9z
The highest exponent in the polynomial is called a degree.
The degree is 1.
The coefficient is 9.
There are two terms in the given polynomial.
Question 6.
t2 – t2 – 10t
Answer:
t2 – t2 – 10t
The highest exponent in the polynomial is called a degree.
The degree is 2.
The coefficient is 10 and 1.
There are three terms in the given polynomial.
Question 7.
2.8x + x3
Answer:
The highest exponent in the polynomial is called a degree.
The degree is 3.
The coefficient is 2.8 and 1.
There are two terms in the given polynomial.
Find the sum or difference.
Question 8.
(b – 10) + (4b – 3)
Answer:
Given,
(b – 10) + (4b – 3)
b – 10 + 4b – 3
3b – 13
So, (b – 10) + (4b – 3) = 3b – 13.
Question 9.
(x2 – x – 2) + (7x2 – x)
Answer:
Given,
(x2 – x – 2) + (7x2 – x)
x² – x – 2 + 7x² – x
8x² – 2x – 2
So, (x2 – x – 2) + (7x2 – x) = 8x² – 2x – 2
Question 10.
(p2 + p + 3) – (-4p2 – p + 3)
Answer:
Given,
(p2 + p + 3) – (-4p2 – p + 3)
p² + p + 3 + 4p² + p – 3
5p² + 2p
(p2 + p + 3) – (-4p2 – p + 3) = 5p² + 2p
Question 11.
(-k + 5) – (3k2 – 6)
Answer:
Given,
(-k + 5) – (3k2 – 6)
-k + 5 – 3k² + 6
-3k² – k + 11
(-k + 5) – (3k2 – 6) = -3k² – k + 11
Question 12.
WHAT IF?
The polynomial -16t2 – 25t + 200 represents the height of the penny after t seconds.
a. Write a polynomial that represents the distance between the penny and the paintbrush after t seconds.
b. Interpret the coefficients of the polynomial in part (a).
Answer:
The coefficients of the polynomials are -16 and -25.
Adding and Subtracting Polynomials 7.1 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
When is a polynomial in one variable in standard form?
Answer:

Question 2.
OPEN-ENDED
Write a trinomial in one variable of degree 5 in standard form.
Answer:

Question 3.
VOCABULARY
How can you determine whether a set of numbers is closed under an operation?
Answer:

Question 4.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.
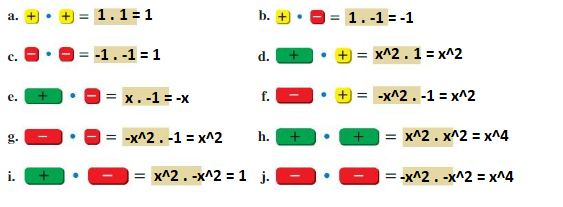
![]()
Answer:

In Exercises 5–12, find the degree of the monomial.
Question 5.
4g
Answer:

Question 6.
23x4
Answer:
The exponent is 4
Question 7.
-1.75k2
Answer:
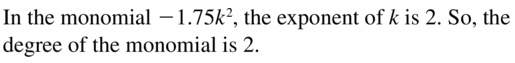
Question 8.
–\(\frac{4}{9}\)
Answer:
The degree of the monomial is 0
Question 9.
s8t
Answer:

Question 10.
8m2n4
Answer:
The degree of the monomial is 2+4=6
Question 11.
9xy3z7
Answer:
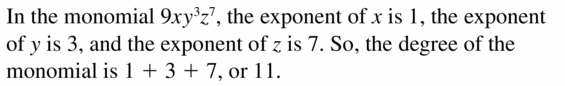
Question 12.
-3q4rs6
Answer:
The degree of the monomial is 4 +1+6=11
In Exercises 13–20, write the polynomial in standard form. Identify the degree and leading coefficient of the polynomial. Then classify the polynomial by the number of terms.
Question 13.
6c2 + 2c4 – c
Answer:

Question 14.
4w11 – w12
Answer:

Question 15.
7 + 3p2
Answer:

Question 16.
8d – 2 – 4d3
Answer:

Question 17.
3t8
Answer:

Question 18.
5z + 2z3 + 3z4
Answer:
The polynomial 5z + 2z3 + 3z4 is in standard form.
The greatest degree of the polynomial is 4. So, the degree is 4.
The leading coefficient is 3.
The polynomial has 3 terms, so it is a trinomial
Question 19.
πr2 – \(\frac{5}{7}\)r8 + 2r5
Answer:

Question 20.
\(\sqrt{7}\)n4
Answer:
The polynomial \(\sqrt{7}\)n4 is in standard form.
The degree of the polynomial is 4.
The coefficient is \(\sqrt{7}\).
The polynomial has 1 term, so it is a monomial.
Question 21.
MODELING WITH MATHEMATICS
The expression \(\frac{4}{3}\) πr3 represents the volume of a sphere with radius r. Why is this expression a monomial? What is its degree?

Answer:
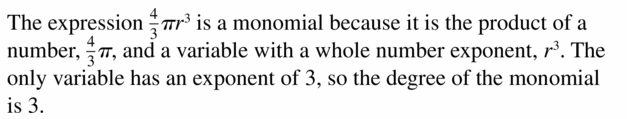
Question 22.
MODELING WITH MATHEMATICS
The amount of money you have after investing $400 for 8 years and $600 for 6 years at the same interest rate is represented by 400x8 + 600x6, where x is the growth factor. Classify the polynomial by the number of terms. What is its degree?
Answer:
Given,
The amount of money you have after investing $400 for 8 years and $600 for 6 years at the same interest rate is represented by 400x8 + 600x6, where x is the growth factor.
The polynomial 400x8 + 600x6 has a degree 8 and is a binomial.
In Exercises 23–30, find the sum.
Question 23.
(5y + 4) + (-2y + 6)
Answer:
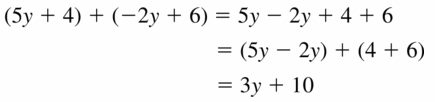
Question 24.
(-8x – 12) + (9x + 4)
Answer:
(-8x – 12) + (9x + 4)
= -8x – 12 + 9x + 4
= -8x + 9x – 12 + 4
= x – 8
Question 25.
(2n2 – 5n – 6) + (-n2 – 3n + 11)
Answer:
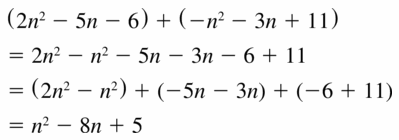
Question 26.
(-3p3 + 5p2 – 2p) + (-p3 – 8p2 – 15p)
Answer:
(-3p3 + 5p2 – 2p) + (-p3 – 8p2 – 15p)
= -3p³ + 5p² – 2p – p³ – 8p² – 15p
= -4p³ – 3p² – 17p
Question 27.
(3g2 – g) + (3g2 – 8g + 4)
Answer:
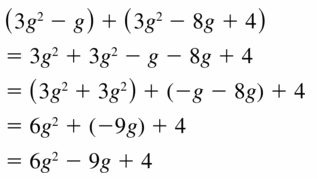
Question 28.
(9r2 + 4r – 7) + (3r2 – 3r)
Answer:
(9r2 + 4r – 7) + (3r2 – 3r)
= 9r² + 4r – 7 + 3r² – 3r
= 9r² + 3r² + 4r – 3r – 7
= 12r² + r – 7
Question 29.
(4a – a3 – 3) + (2a3 – 5a2 + 8)
Answer:
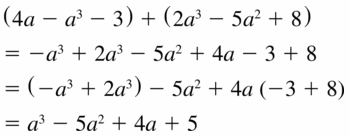
Question 30.
(s3 – 2s – 9) + (2s2 – 6s3 + s)
Answer:
(s3 – 2s – 9) + (2s2 – 6s3 + s)
s³ – 2s – 9 + 2s² – 6s³ + s
s³ – 6s³ + 2s² – 2s + s – 9
-5s³ + 2s² – s – 9
(s3 – 2s – 9) + (2s2 – 6s3 + s) = -5s³ + 2s² – s – 9
In Exercises 31–38, find the difference.
Question 31.
(d – 9) – (3d – 1)
Answer:
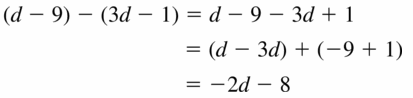
Question 32.
(6x + 9) – (7x + 1)
Answer:
(6x + 9) – (7x + 1)
6x + 9 – 7x – 1
6x – 7x + 9 – 1
-x + 8
(6x + 9) – (7x + 1) = -x + 8
Question 33.
(y2 – 4y + 9) – (3y2 – 6y – 9)
Answer:
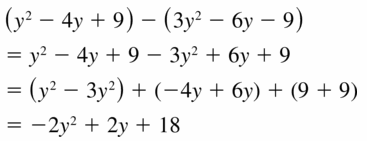
Question 34.
(4m2 – m + 2) – (-3m2 + 10m + 4)
Answer:
(4m2 – m + 2) – (-3m2 + 10m + 4)
4m² – m + 2 + 3m² – 10m – 4
4m² + 3m² – m – 10m + 2 – 4
7m² – 11m – 2
Question 35.
(k3 – 7k + 2) – (k2 – 12)
Answer:
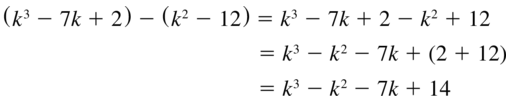
Question 36.
(-r – 10) – (-4r3 + r2 + 7r)
Answer:
(-r – 10) – (-4r3 + r2 + 7r)
-r – 10 + 4r³ – r² – 7r
4r³ – r² – 7r – r – 10
4r³ – r² – 8r – 10
Question 37.
(t4 – t2 + t) – (12 – 9t2 – 7t)
Answer:
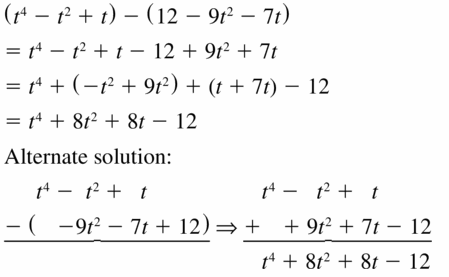
Question 38.
(4d – 6d3 + 3d2) – (10d3 + 7d – 2)
Answer:
(4d – 6d3 + 3d2) – (10d3 + 7d – 2)
4d – 6d³ + 3d² – 10d³ – 7d + 2
-16d³ + 3d² – 3d + 2
(4d – 6d3 + 3d2) – (10d3 + 7d – 2) = -16d³ + 3d² – 3d + 2
ERROR ANALYSIS In Exercises 39 and 40, describe and correct the error in finding the sum or difference.
Question 39.
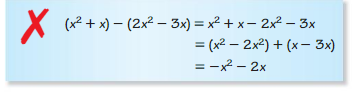
Answer:
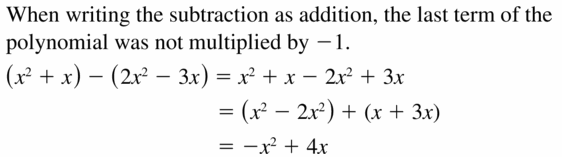
Question 40.
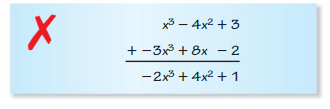
Answer:
(x³ – 4x² + 3) + (-3x³ + 8x – 2)
x³ – 3x³ – 4x² + 8x + 3 – 2
-2x³ – 4x² + 8x + 1
Question 41.
MODELING WITH MATHEMATICS
The cost (in dollars)of making b bracelets is represented by 4 + 5b. The cost (in dollars) of making b necklaces is represented by 8b + 6. Write a polynomial that represents how much more it costs to make b necklaces than b bracelets.

Answer:
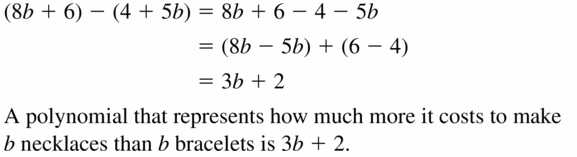
Question 42.
MODELING WITH MATHEMATICS
The number of individual memberships at a fitness center in m months is represented by 142 + 12m. The number of family memberships at the fitness center in m months is represented by 52 + 6m. Write a polynomial that represents the total number of memberships at the fitness center.
Answer:
Given,
The number of individual memberships at a fitness center in m months is represented by 142 + 12m.
The number of family memberships at the fitness center in m months is represented by 52 + 6m.
= 142 + 12m + 52 + 6m
= 18m + 194
So, the total number of memberships at the fitness center is 18m + 194.
In Exercises 43–46, find the sum or difference.
Question 43.
(2s2 – 5st – t2) – (s2 + 7st – t2)
Answer:
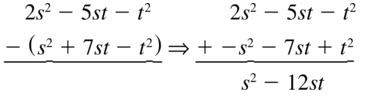
Question 44.
(a2 – 3ab + 2b2) + (-4a2 + 5ab – b2)
Answer:
(a2 – 3ab + 2b2) + (-4a2 + 5ab – b2)
a2 – 3ab + 2b2 -4a2 + 5ab – b2
-3a2 + b2 +2ab
So, (a2 – 3ab + 2b2) + (-4a2 + 5ab – b2) = -3a2 + b2 +2ab
Question 45.
(c2 – 6d2) + (c2 – 2cd + 2d2)
Answer:
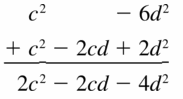
Question 46.
(-x2 + 9xy) – (x2 + 6xy – 8y2)
Answer:
(-x2 + 9xy) – (x2 + 6xy – 8y2)
-x2 + 9xy – x2 – 6xy + 8y2)
-2x2 + 3xy + 8y2
REASONING In Exercises 47–50, complete the statement with always, sometimes, or never. Explain your reasoning.
Question 47.
The terms of a polynomial are ________ monomials.
Answer:
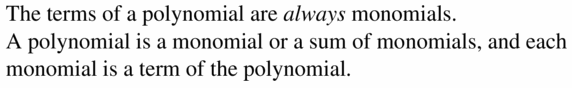
Question 48.
The difference of two trinomials is _________ a trinomial.
Answer: The difference of two trinomials is sometimes a trinomial.
Question 49.
A binomial is ________ a polynomial of degree 2.
Answer:
Question 50.
The sum of two polynomials is _________ a polynomial.
Answer: The sum of two polynomials is always a polynomial.
MODELING WITH MATHEMATICS The polynomial −16t2 – v0t – s0 represents the height (in feet) of an object, where v0 is the initial vertical velocity (in feet per second), s0 is the initial height of the object (in feet), and t is the time (in seconds). In Exercises 51 and 52, write a polynomial that represents the height of the object. Then nd the height of the object after 1 second.
Question 51.
You throw a water balloon from a building.
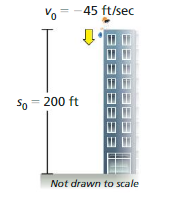
Answer:
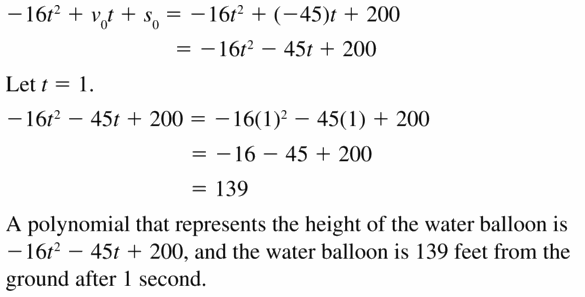
Question 52.
You bounce a tennis ball on a racket.
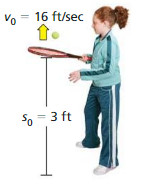
Answer:
v0 = 16 ft/sec
s0 = 3 ft
−16t2 – v0t – s0
-16t² – 16t – 3
-16(1)² – 16(1) – 3
-16 – 16 – 3
= -35 is less than 1.
Question 53.
MODELING WITH MATHEMATICS
You drop a ball from a height of 98 feet. At the same time, your friend throws a ball upward. The polynomials represent the heights (in feet) of the balls after t seconds.
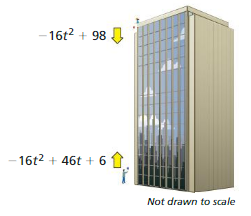
a. Write a polynomial that represents the distance between your ball and your friend’s ball after t seconds.
b. Interpret the coefficients of the polynomial in part (a).
Answer:

Question 54.
MODELING WITH MATHEMATICS
During a 7-year period, the amounts (in millions of dollars) spent each year on buying new vehicles N and used vehicles U by United States residents are modeled by the equations
N = -0.028t3 + 0.06t2+ 0.1t + 17
U = -0.38t2 + 1.5t + 42
where t = 1 represents the first year in the 7-year period.
a. Write a polynomial that represents the total amount spent each year on buying new and used vehicles in the 7-year period.
Answer:
N = -0.028t3 + 0.06t2+ 0.1t + 17
U = -0.38t2 + 1.5t + 42
S = N + U
S = -0.028t3 + 0.06t2+ 0.1t + 17 + (-0.38t2 + 1.5t + 42)
S = -0.028t3 + 0.06t2+ 0.1t + 17 – 0.38t2 + 1.5t + 42
S = -0.028t3 – 0.32t2 + 1.6t + 59
b. How much is spent on buying new and used vehicles in the fifth year?
Answer:
S = -0.028t3 – 0.32t2 + 1.6t + 59
t = 5
S = -0.028(5)3 – 0.32(5)2 + 1.6(5) + 59
S = -3.5 – 8 + 8 + 59
S = $55.5
Question 55.
MATHEMATICAL CONNECTIONS
Write the polynomial in standard form that represents the perimeter of the quadrilateral.
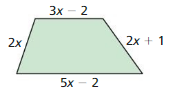
Answer:
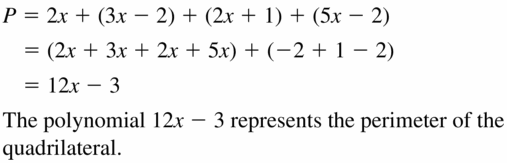
Question 56.
HOW DO YOU SEE IT?
The right side of the equation of each line is a polynomial.
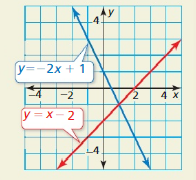
a. The absolute value of the difference of the two polynomials represents the vertical distance between points on the lines with the same x-value. Write this expression.
Answer:
(x – 2) – (-2x + 1)
= x – 2 + 2x – 1
= 3x – 3
= 3(x – 1)
It represents vertical distance between points on the lines with the same x value.
d = 3|x – 1|
b. When does the expression in part (a) equal 0? How does this value relate to the graph?
Answer:
d = 3(x – 1)
3(x – 1) = 0
x – 1 = 0
x = 1
It also represents the point of intersection of the two lines.
Question 57.
MAKING AN ARGUMENT
Your friend says that when adding polynomials, the order in which you add does not matter. Is your friend correct? Explain.
Answer:

Question 58.
THOUGHT PROVOKING
Write two polynomials whose sum is x2 and whose difference is 1.
Answer:
p(x) + q(x) = x²
p(x) – q(x) = 1
p(x) = ax² + b
q(x) = cx² + d
p(x) + q(x) = (a + c)x² + (b + d) = x²
a + c = 1
b + d = 0
p(x) – q(x) = (a – c)x² + (b – d) = 1
a – c = 0
b – d = 1
b = -d
b – d = 1
b + b = 1
2b = 1
b = 1/2
d = -b = -1/2
a + c = 1
a + a = 1
2a = 1
a = 1/2
a = 1/2 = c
p(x) = 1/2 x² + 1/2
q(x) = 1/2 x² – 1/2
Question 59.
REASONING
Determine whether the set is closed under the given operation. Explain.
a. the set of negative integers; multiplication
b. the set of whole numbers; addition
Answer:

Question 60.
PROBLEM SOLVING
You are building a multi-level deck.
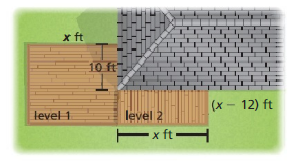
a. For each level, write a polynomial in standard form that represents the area of that level. Then write the polynomial in standard form that represents the total area of the deck.
Answer:
Let us find the area of level 1 of the deck.
Level 1 is a rectangle having length x and breadth 10 + (x – 12)
A = x(10 + (x – 12))
A = 10x + x² – 12x = x² – 2x
Level 2 is a rectangle having length x and breadth (x – 12)
A’ = x(x – 12)
A’ = x² – 12x
x² – 2x + x² – 12x = 2x² – 14x
Thus the polynomial represents the area of the deck.
b. What is the total area of the deck when x = 20?
Answer:
A = 2x² – 14x
x = 20
A = 2(20)² – 14(20)
A = 800 – 280
A = 520
The total area of the deck when x = 20 is 520 square feet.
c. A gallon of deck sealant covers 400 square feet. How many gallons of sealant do you need to cover the deck in part (b) once? Explain.
Answer:
A gallon of deck sealant covers 400 square feet.
400 sq. ft/ 1 gallon = 520 sq.ft/x gallons
400/1 = 520/x
x × 400 = 520
x = 520/400
x = 1.3
Question 61.
PROBLEM SOLVING
A hotel installs a new swimming pool and a new hot tub.
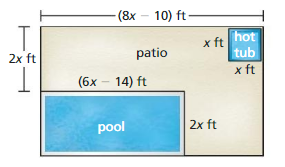
a. Write the polynomial in standard form that represents the area of the patio.
b. The patio will cost $10 per square foot. Determine the cost of the patio when x = 9.
Answer:

Maintaining Mathematical Proficiency
Simplify the expression.
Question 62.
2(x – 1) + 3(x + 2)
Answer:
2(x – 1) + 3(x + 2)
2x – 2 + 3x + 6
2x + 3x – 2 + 6
5x + 4
2(x – 1) + 3(x + 2) = 5x + 4
Question 63.
8(4y – 3) + 2(y – 5)
Answer:
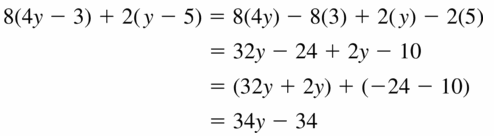
Question 64.
5(2r + 1) – 3(-4r + 2)
Answer:
5(2r + 1) – 3(-4r + 2)
10r + 5 + 12r – 6
10r + 12r + 5 – 6
22r – 1
5(2r + 1) – 3(-4r + 2) = 22r – 1
Lesson 7.2 Multiplying Polynomials
Essential Question How can you multiply two polynomials?
EXPLORATION 1
Multiplying Monomials Using Algebra Tiles
Work with a partner. Write each product. Explain your reasoning.
Answer:
EXPLORATION 2
Multiplying Binomials Using Algebra Tiles

Work with a partner. Write the product of two binomials modeled by each rectangular array of algebra tiles. In parts (c) and (d), first draw the rectangular array of algebra tiles that models each product.
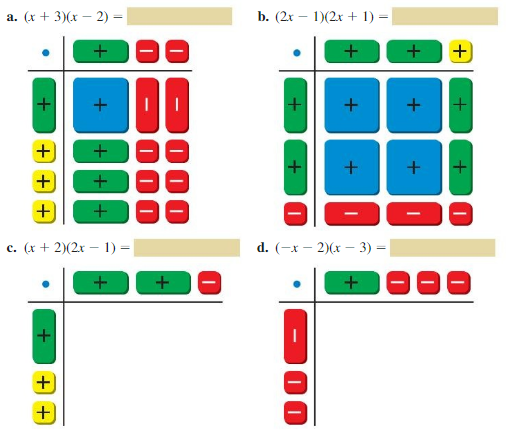
Answer:
a. (x + 3)(x – 2)
x(x – 2) + 3(x – 2)
x² – 2x + 3x – 6
x² + x – 6
(x + 3)(x – 2) = x² + x – 6
b. (2x – 1)(2x + 1)
2x(2x + 1) – 1(2x + 1)
4x² + 2x – 2x – 1
4x² – 1
(2x – 1)(2x + 1) = 4x² – 1
c. (x + 2)(2x – 1)
x(2x – 1) + 2(2x – 1)
2x² – x + 4x – 2
2x² + 3x – 2
(x + 2)(2x – 1) = 2x² + 3x – 2
d. (-x – 2)(x – 3)
-x(x – 3) – 2(x – 3)
-x² + 3x – 2x + 6
-x² + x + 6
So, (-x – 2)(x – 3) = -x² + x + 6
Communicate Your Answer
Question 3.
How can you multiply two polynomials?
Answer:
First, multiply each term in one polynomial by each term in the other polynomial using the distributive law. Add the powers of the same variables using the exponent rule. Then, simplify the resulting polynomial by adding or subtracting the like terms.
Question 4.
Give another example of multiplying two binomials using algebra tiles that is similar to those in Exploration 2.
Answer:
Example:
(x + 3)(x – 2)
x(x) + x(-2) + 3(x) + 3(-2)
x² – 2x + 3x – 6
x² + x – 6
Example 2:
(2x – 1)(2x + 1)
2x(2x) + 2x(1) – 1(2x) – 1(1)
4x² + 2x – 2x – 1
4x² – 1
Thus the simplified forms of the products of two binomials modeled by each rectangular array of algebra tiles are
(2x – 1)(2x + 1) = 4x² – 1
(x + 3)(x – 2) = x² + x – 6
Monitoring Progress
Use the Distributive Property to find the product.
Question 1.
(y + 4)(y + 1)
Answer:
Given,
(y + 4)(y + 1)
y(y + 1) + 4(y + 1)
y² + y + 4y + 4
y² + 5y + 4
So, (y + 4)(y + 1) = y² + 5y + 4
Question 2.
(z – 2)(z + 6)
Answer:
(z – 2)(z + 6)
z(z + 6) – 2(z + 6)
z² + 6z – 2z – 12
z² + 4z – 12
So, (z – 2)(z + 6) = z² + 4z – 12
Use a table to find the product.
Question 3.
(p + 3)(p – 8)
Answer:
(p + 3)(p – 8) = p(p – 8) + 3(p – 8)
= p² – 8p + 3p – 24
= p² – 5p – 24
So, (p + 3)(p – 8) = p² – 5p – 24
Question 4.
(r – 5)(2r – 1)
Answer:
(r – 5)(2r – 1) = r(2r – 1) – 5(2r – 1)
= 2r² – r – 10r + 5
= 2r² – 11r + 5
(r – 5)(2r – 1) = 2r² – 11r + 5
Use the FOIL Method to find the product.
Question 5.
(m – 3)(m – 7)
Answer:
(m – 3)(m – 7) = m(m) + m(-7) – 3(m) – 3(-7)
= m² – 7m – 3m + 21
= m² – 10m + 21
(m – 3)(m – 7) = m² – 10m + 21
Question 6.
(x – 4)(x + 2)
Answer:
(x – 4)(x + 2) = x(x + 2) -4(x + 2)
= x² + 2x – 4x
Question 7.
( 2u + \(\frac{1}{2}\))( u – \(\frac{3}{2}\))
Answer:
( 2u + \(\frac{1}{2}\))( u – \(\frac{3}{2}\)) = 2u(u) + 2u(\(\frac{3}{2}\)) + \(\frac{1}{2}\)(u) – (\(\frac{1}{2}\))(\(\frac{3}{2}\))
= 2u² + 3u + \(\frac{1}{2}\)u – \(\frac{3}{4}\)
= 2u² + 3\(\frac{1}{2}\)u – \(\frac{3}{4}\)
Question 8.
(n + 2)(n2 + 3)
Answer:
(n + 2)(n2 + 3)
= n(n2 + 3) + 2(n2 + 3)
= n³ + 3n + 2n² + 6
= n³ + 2n² + 3n + 6
So, (n + 2)(n2 + 3) =n³ + 2n² + 3n + 6
Find the product.
Question 9.
(x + 1)(x2 + 5x + 8)
Answer:
(x + 1)(x2 + 5x + 8)
= x(x2 + 5x + 8) + 1(x2 + 5x + 8)
= x³ + 5x² + 8x + x² + 5x + 8
= x³ + 6x² + 13x + 8
So, (x + 1)(x2 + 5x + 8) = x³ + 6x² + 13x + 8
Question 10.
(n – 3)(n2 – 2n + 4)
Answer:
(n – 3)(n2 – 2n + 4)
= n(n2 – 2n + 4) – 3(n2 – 2n + 4)
= n³ – 2n² + 4n – 3n² + 6n – 12
= n³ – 5n² + 10n – 12
(n – 3)(n2 – 2n + 4) = n³ – 5n² + 10n – 12
Question 11.
WHAT IF?
In Example 5(a), how does the polynomial change when the longer base is extended by 1 foot? Explain.
Answer:
Area of a trapezoid = 1/2 × h [b1 + b2]
= 1/2 (x – 7)[x + (x + 11)]
= 1/2 (x – 7)(2x + 11)
= 1/2[x(2x + 11) + (-7)(2x + 11)]
= 1/2(2x² + 11x – 14x – 77)
= 1/2(2x² – 4x – 77)
Multiplying Polynomials 7.2 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
Describe two ways to find the product of two binomials.
Answer:

Question 2.
WRITING
Explain how the letters of the word FOIL can help you to remember how to multiply two binomials.
Answer:
The multiplication of polynomials using the FOIL method involves multiplying the first, outer, inner and last terms together and calculating the value.
Example:
(x + 3)(x + 5) = x(x + 5) + 3(x + 5)
= x² + 5x + 3x + 15
= x² + 8x + 15
Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, use the Distributive Property to find the product.
Question 3.
(x + 1)(x + 3)
Answer:
Question 4.
(y + 6)(y + 4)
Answer:
(y + 6)(y + 4) = y(y + 4) + 6(y + 4)
= y² + 4y + 6y + 24
= y² + 10y + 24
So, (y + 6)(y + 4) = y² + 10y + 24
Question 5.
(z – 5)(z + 3)
Answer:
Question 6.
(a + 8)(a – 3)
Answer:
(a + 8)(a – 3) = a(a – 3) + 8(a – 3)
= a² – 3a + 8a – 24
= a² + 5a – 24
Question 7.
(g – 7)(g – 2)
Answer:
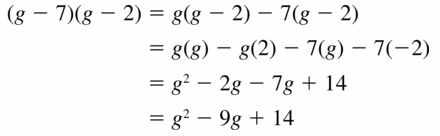
Question 8.
(n – 6)(n – 4)
Answer:
(n – 6)(n – 4) = n(n – 4) – 6(n – 4)
= n² – 4n – 6n + 24
= n² – 10n + 24
Question 9.
(3m + 1)(m + 9)
Answer:
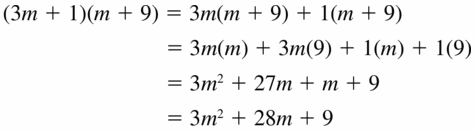
Question 10.
(5s + 6)(s – 2)
Answer:
(5s + 6)(s – 2) = 5s(s – 2) + 6(s – 2)
= 5s² – 10s + 6s – 12
= 5s² – 4s – 12
In Exercises 11–18, use a table to find the product.
Question 11.
(x + 3)(x + 2)
Answer:
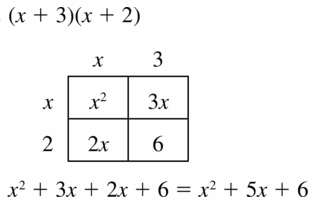
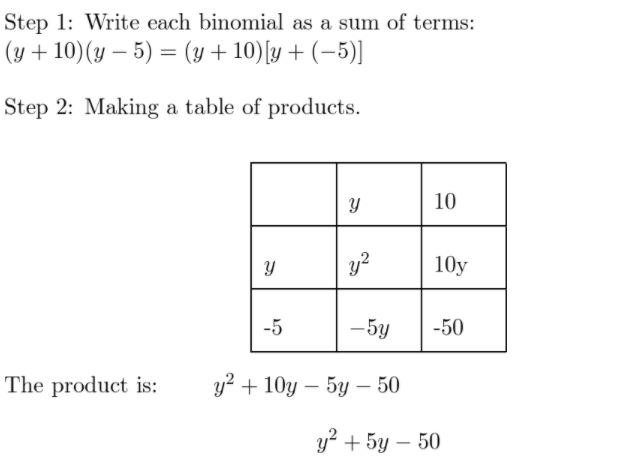
Question 12.
(y + 10)(y – 5)
Answer:
Question 13.
(h – 8)(h – 9)
Answer:
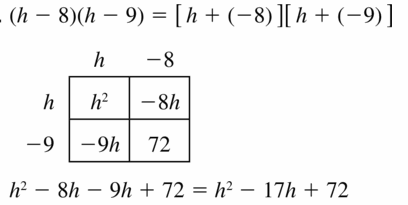
Question 14.
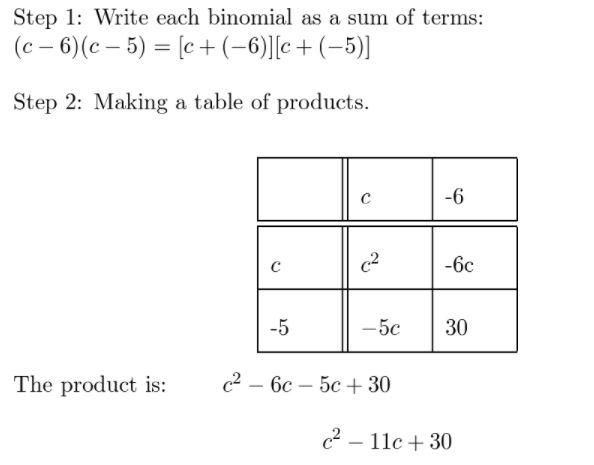
(c – 6)(c – 5)
Answer:
Question 15.
(3k – 1)(4k + 9)
Answer:
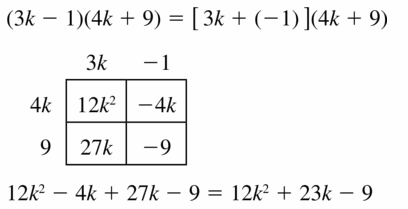
Question 16.
(5g + 3)(g + 8)
Answer:

Question 17.
(-3 + 2j)(4j – 7)
Answer:
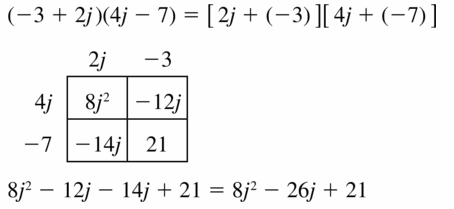
Question 18.
(5d – 12)(-7 + 3d)
Answer:

ERRORANALYSIS
In Exercises 19 and 20, describe and correct the error in finding the product of the binomials.
Question 19.
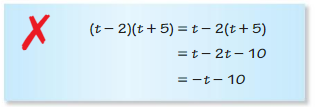
Answer:
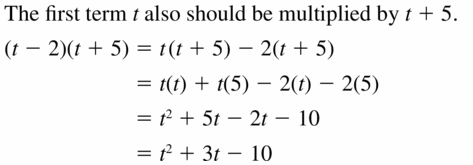
Question 20.

Answer:

In Exercises 21–30, use the FOIL Method to find the product.
Question 21.
(b + 3)(b + 7)
Answer:
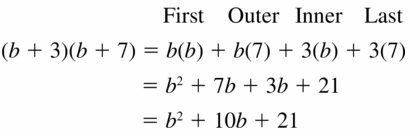
Question 22.
(w + 9)(w + 6)
Answer:
(w + 9)(w + 6) = w(w) + w(9) + w(6) + 9(6)
= w² + 9w + 6w + 54
= w² + 15w + 54
Question 23.
(k + 5)(k – 1)
Answer:
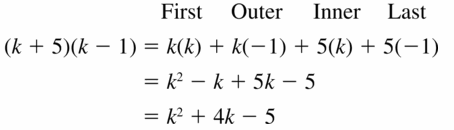
Question 24.
(x – 4)(x + 8)
Answer:
(x – 4)(x + 8) = x(x) + x(-4) + x(8) + 8(-4)
= x² – 4x + 8x – 32
= x² + 4x – 32
Question 25.
(q – \(\frac{3}{4}\)) (q + \(\frac{1}{4}\))
Answer:
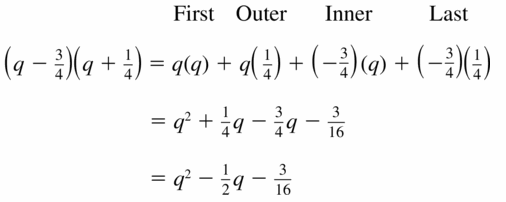
Question 26.
(z – \(\frac{5}{3}\)) (z – \(\frac{2}{3}\))
Answer:
(z – \(\frac{5}{3}\)) (z – \(\frac{2}{3}\)) = z(z) + z(\(\frac{2}{3}\)) – \(\frac{5}{3}\)(z) + (-\(\frac{2}{3}\))(-\(\frac{5}{3}\))
= z² + \(\frac{2}{3}\)z – \(\frac{5}{3}\)z + \(\frac{10}{9}\)
Question 27.
(9 – r)(2 – 3r)
Answer:
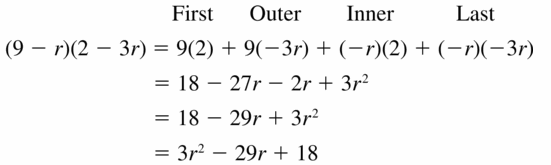
Question 28.
(8 – 4x)(2x + 6)
Answer:
(8 – 4x)(2x + 6) = 8(2x) – 4x(2x) – 4x(6) + 8(6)
= 16x – 8x² – 24x + 48
Question 29.
(w + 5)(w2 + 3w)
Answer:
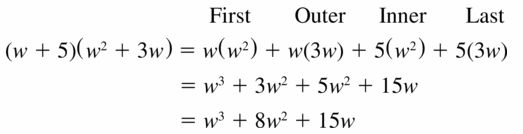
Question 30.
(v – 3)(v2 + 8v)
Answer:
(v – 3)(v2 + 8v) = v(v2) + v(8v) – 3(v2) – 3(8v)
= v³ + 8v² – 3v² – 24v
= v³ + 5v² – 24v
MATHEMATICAL CONNECTIONS In Exercises 31– 34, write a polynomial that represents the area of the shaded region.
Question 31.
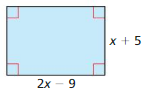
Answer:

Question 32.
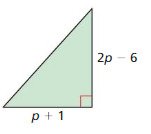
Answer:
A = length × width
A = (p + 1)(2p – 6)
= p(2p – 6) + 1(2p – 6)
= 2p² – 6p + 2p – 6
= 2p² – 4p – 6
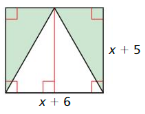
Question 33.
Answer:

Question 34.
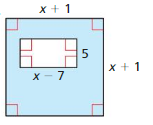
Answer:
Area of inner rectangle = 5(x – 7)
= 5x – 35
Area of square = s × s
A = (x + 1)(x + 1)
A = x² + 2x + 1
Total = x² + 2x + 1 – 5x + 35
= x² – 3x + 36
In Exercises 35–42, find the product.
Question 35.
(x + 4)(x2 + 3x + 2)
Answer:
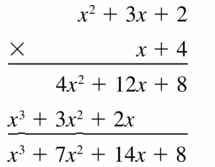
Question 36.
(f + 1)(f2 + 4f + 8)
Answer:
(f2 + 4f + 8)
× (f + 1)
f(f2 + 4f + 8) + 1(f2 + 4f + 8)
f³ + 4f² + 8f + f² + 4f + 8
Combine the like terms.
f³ + 5f² + 12f + 8
So, (f + 1)(f2 + 4f + 8) = f³ + 5f² + 12f + 8
Question 37.
(y + 3)( y2 + 8y – 2)
Answer:
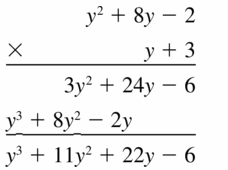
Question 38.
(t – 2)(t2 – 5t + 1)
Answer:
(t2 – 5t + 1)
× (t – 2)
t(t2 – 5t + 1) – 2(t2 – 5t + 1)
= t³ – 5t² + t – 2t² + 10t – 2
= t³ – 7t² + 11t – 2
Question 39.
(4 – b)(5b2 + 5b – 4)
Answer:
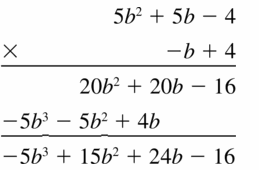
Question 40.
(d + 6)(2d2 – d + 7)
Answer:
(2d2 – d + 7)
× (d + 6)
= d(2d2 – d + 7) + 6(2d2 – d + 7)
= 2d³ – d² + 7d + 12d² – 6d + 42
= 2d³ – d² + 12d² + 7d – 6d + 42
= 2d³ + 11 d² + d + 42
Question 41.
(3e2 – 5e + 7)(6e + 1)
Answer:
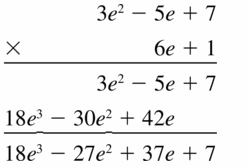
Question 42.
(6v2 + 2v – 9)(4 – 5v)
Answer:
(6v2 + 2v – 9)(4 – 5v)
4(6v2 + 2v – 9) – 5v(6v2 + 2v – 9)
24v² + 8v – 36 – 30v³ – 10v² + 45v
– 30v³ + 14v² + 53v – 36
Question 43.
MODELING WITH MATHEMATICS
The football field is rectangular.
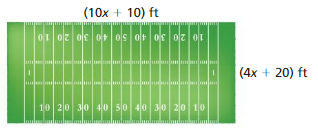
a. Write a polynomial that represents the area of the football field.
b. Find the area of the football field when the width is 160 feet.
Answer:

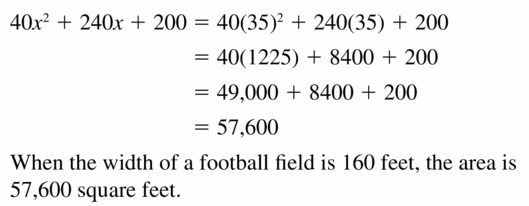
Question 44.
MODELING WITH MATHEMATICS
You design a frame to surround a rectangular photo. The width of the frame is the same on every side, as shown.
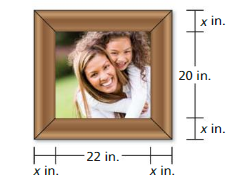
a. Write a polynomial that represents the combined area of the photo and the frame.
Answer:
Width = 2x inch
Combined length is equal to the sum of lengths of the photo and the frame.
So, the combined length = 22 + 2x
Combined width = 20 + 2x
Area = length × width
A = (22 + 2x)(20 + 2x)
A = 440 + 44x + 40x + 4x²
A = 4x² + 84x + 440
b. Find the combined area of the photo and the frame when the width of the frame is 4 inches.
Answer:
The combined length is equal to the sum of lengths of the photo and the frame.
So, the combined length = 22 + 2x
Combined width = 20 + 2x
Combined area of the photo and the frame is 4x² + 84x + 440
2x = 4
x = 2
A = 4x² + 84x + 440
x = 2
A = 4(2)² + 84(2) + 440
A = 16 + 168 + 440
A = 624 sq. in
So, the combined area is 624 sq. in.
Question 45.
WRITING
When multiplying two binomials, explain how the degree of the product is related to the degree of each binomial.
Answer:

Question 46.
THOUGHT PROVOKING
Write two polynomials that are not monomials whose product is a trinomial of degree 3.
Answer:
(x² – x)(x + 1)
= x²(x + 1) – x(x + 1)
= x²(x) + x²(1) – x(x) – x(1)
= x³ + x² – x – 1
So, this is trinomial has a degree 3.
Question 47.
MAKING AN ARGUMENT
Your friend says the FOIL Method can be used to multiply two trinomials. Is your friend correct? Explain your reasoning.
Answer:

Question 48.
HOW DO YOU SEE IT?
The table shows one method of finding the product of two binomials.

a. Write the two binomials being multiplied.
Answer:
The first binomial is -4x + 3
The second binomial is -8x – 9
b. Determine whether a, b, c, and d will be positive or negative when x > 0.
Answer:
The two binomials are -4x + 3 and -8x – 9
a: (-4x)(-8x) is positive
b: (3)(-8x) is negative
c: (-4x)(-9) is positive
d: (3)(-9) is negative
Hence, when x >0
a – positive
b – negative
c – positive
d – negative
Question 49.
COMPARING METHODS
You use the Distributive Property to multiply (x + 3)(x – 5). Your friend uses the FOIL Method to multiply (x – 5)(x + 3). Should your answers be equivalent? Justify your answer.
Answer:

Question 50.
USING STRUCTURE
The shipping container is a rectangular prism. Write a polynomial that represents the volume of the container.

Answer:
V = lbh
V = (4x – 3)(x + 1)(x + 2)
= (4x – 3)(x² + 2x + x + 2)
= (4x – 3)(x² + 3x + 2)
= 4x³ + 12x² + 8x – 3x² – 9x – 6
= 4x³ + 9x² – x – 6
V = 4x³ + 9x² – x – 6
Question 51.
ABSTRACT REASONING
The product of (x + m)(x + n) is x2 + bx + c.
a. What do you know about m and n when c > 0?
b. What do you know about m and n when c < 0?
Answer:
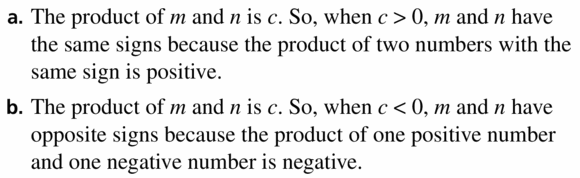
Maintaining Mathematical Proficiency
Write the absolute value function as a piecewise function.
Question 52.
y = |x| + 4
Answer:
y = x + 15 x > 0
y = -x + 15 x < 0
Question 53.
y = 6|x – 3|
Answer:
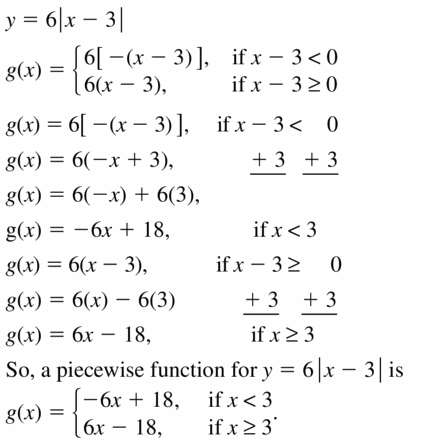
Question 54.
y = -4|x + 2|
Answer:
y = -4|x + 2|
-4(x+ 2)
= -4x – 8
y = -4(-(x + 2))
y = -4(-x – 2)
y = 4x + 8
Simplify the expression. Write your answer using only positive exponents.
Question 55.
102 • 109
Answer:
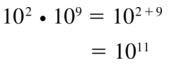
Question 56.
\(\frac{x^{5} \cdot x}{x^{8}}\)
Answer:
\(\frac{x^{5} \cdot x}{x^{8}}\)
= x6/x8
= 1/x²
Question 57.
(3z6)-3
Answer:
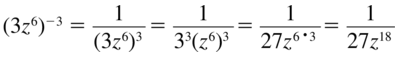
Question 58.
\(\left(\frac{2 y^{4}}{y^{3}}\right)^{-2}\)
Answer:
\(\left(\frac{2 y^{4}}{y^{3}}\right)^{-2}\)
(2y)-2
= 1/4y²
Lesson 7.3 Special Products of Polynomials
Essential Question What are the patterns in the special products (a+ b)(a – b), (a + b)2, and (a – b)2?
EXPLORATION 1
Finding a Sum and Difference Pattern
Work with a partner. Write the product of two binomials modeled by each rectangular array of algebra tiles.
Answer:
a. (x + 2)(x – 2) = x(x – 2) + 2(x – 2)
= x² – 2x + 2x – 4
= x² – 4
b. (2x – 1)(2x + 1)
= 2x(2x + 1) – 1(2x + 1)
= 4x² + 2x – 2x – 1
= 4x² – 1
EXPLORATION 2
Finding the Square of a Binomial Pattern
Work with a partner. Draw the rectangular array of algebra tiles that models each product of two binomials. Write the product.
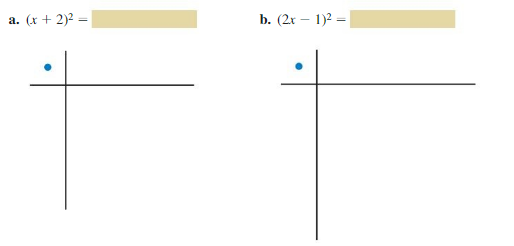
Answer:
Communicate Your Answer
Question 3.
What are the patterns in the special products (a + b)(a – b), (a + b)2, and (a – b)2?

Answer:
(a + b)(a – b)
Apply distributive property
a(a – b) + b(a – b)
a² – ab + ba – b²
(a + b)(a – b) = a² – b²
So, (a + b)(a – b) = a² – b²
(a + b)(a + b)
Apply distributive property
a(a + b) + b(a + b)
a² + ab + ba + b² = a² + 2ab + b²
(a – b)(a – b)
Apply distributive property
a(a – b) – b(a – b)
a² – ab – ba + b² = a² – 2ab + b²
Question 4.
Use the appropriate special product pattern to find each product. Check your answers using algebra tiles.
a. (x + 3)(x – 3)
b. (x – 4)(x + 4)
c. (3x + 1)(3x – 1)
d. (x + 3)2
e. (x – 2)2
f. (3x + 1)2
Answer:
a. (x + 3)(x – 3)
It is in the form of (a + b)(a – b) = a² – b²
(x + 3)(x – 3) = x² – 3²
= x² – 9
b. (x – 4)(x + 4)
It is in the form of (a + b)(a – b) = a² – b²
(x – 4)(x + 4) = x² – 4²
= x² – 16
c. (3x + 1)(3x – 1)
It is in the form of (a + b)(a – b) = a² – b²
(3x + 1)(3x – 1) = (3x)² – 1
= 9x² – 1
d. (x + 3)²
It is in the form of (a + b)2 = a² + 2ab + b²
= (x)² + (3)² + 2(x)(3)
= x² + 9 + 6x
e. (x – 2)²
It is in the form of (a – b)2 = a² – 2ab + b²
(x – 2)² = (x)² + (2)² + 2(x)(2)
= x² + 4 + 4x
f. (3x + 1)²
It is in the form of (a + b)2 = a² + 2ab + b²
= (3x)² + (1)² + 2(3x)(1)
= 9x² + 1 + 6x
Monitoring Progress
Find the product.
Question 1.
(x + 7)2
Answer:
(x + 7)²
It is in the form of (a + b)² = a² + b² + 2ab
(x + 7)² = x² + 7² + 2(x)(7)
= x² + 49 + 14x
So, (x + 7)² = x² + 49 + 14x
Question 2.
(7x – 3)2
Answer:
(7x – 3)²
It is in the form of (a – b)² = a² + b² – 2ab
(7x – 3)² = (7x)² + (3)² – 2(7x)(3)
= 49x² + 9 – 42x
= 49x² – 42x + 9
So, (7x – 3)² = 49x² – 42x + 9
Question 3.
(4x – y)2
Answer:
(4x – y)²
It is in the form of (a – b)² = a² + b² – 2ab
(4x – y)² = (4x)² + (y)² – 2(4x)(y)
= 16x² + y² – 8xy
So, (4x – y)² = 16x² + y² – 8xy
Question 4.
(3m + n)2
Answer:
(3m + n)²
It is in the form of (a + b)² = a² + b² + 2ab
(3m + n)² = (3m)² + (n)² + 2(3m)(n)
= 9m² + n² + 6mn
So, (3m + n)² = 9m² + n² + 6mn
Find the product.
Question 5.
(x + 10)(x – 10)
Answer:
Given,
(x + 10)(x – 10)
It is in the form of (a + b)(a – b) = a² – b²
(x + 10)(x – 10) = x² – (10)²
= x² – 100
So, (x + 10)(x – 10) = x² – 100
Question 6.
(2x + 1)(2x – 1)
Answer:
(2x + 1)(2x – 1)
It is in the form of (a + b)(a – b) = a² – b²
(2x + 1)(2x – 1) = (2x)² – (1)²
= 4x² – 1
(2x + 1)(2x – 1) = 4x² – 1
Question 7.
(x + 3y)(x – 3y)
Answer:
(x + 3y)(x – 3y)
It is in the form of (a + b)(a – b) = a² – b²
(x + 3y)(x – 3y) = (x)² – (3y)²
= x² – 9y²
(x + 3y)(x – 3y) = x² – 9y²
Question 8.
Describe how to use special product patterns to find 212.
Answer:
21² = (20 + 1)²
It is in the form of (a + b)² = a² + b² + 2ab
(20 + 1)² = (20)² + (1)² + 2(20)(1)
= 400 + 1 + 40
= 441
21² = (20 + 1)² = 441
Question 9.
Each of two dogs has one black gene (B) and one white gene (W). The Punnett square shows the possible gene combinations of an offspring and the resulting colors.
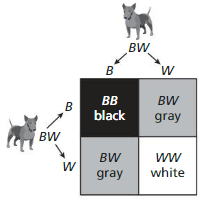
a. What percent of the possible gene combinations result in black?
Answer:
Given,
Each of two dogs has one black gene (B) and one white gene (W). The Punnett square shows the possible gene combinations of an offspring and the resulting colors.
3/4 = 75%
The possible gene combinations result in black is 75 percent.
b. Show how you could use a polynomial to model the possible gene combinations of the offspring.
Answer:
Given,
Each of two dogs has one black gene (B) and one white gene (W). The Punnett square shows the possible gene combinations of an offspring and the resulting colors.
0.5B + 0.5W
There is an equivalent chance that the offspring receives a black or a white gene from each parent.
(0.5B + 0.5W)²
So, to find the possible gene combinations of the offspring, we can solve this product using the square of the binomial pattern.
Special Products of Polynomials 7.3 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Explain how to use the square of a binomial pattern.
Answer:
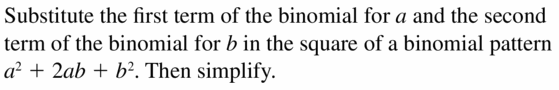
Question 2.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.

Answer:
(x + 2)(x – 3) does not belong with the other three. Because it is not in the form of (a + b)(a – b)
Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, find the product.
Question 3.
(x + 8)2
Answer:
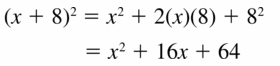
Question 4.
(a – 6)2
Answer:
(a – 6)2
It is in the form of (a – b)² = a² + b² – 2ab
(a – 6)² = a² + 6² – 2a(6)
= a² + 36 – 12a
So, (a – 6)2 = a² + 36 – 12a
Question 5.
(2f – 1)2
Answer:
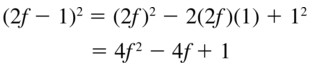
Question 6.
(5p + 2)2
Answer:
(5p + 2)2
It is in the form of (a + b)² = a² + b² + 2ab
(5p + 2)² = (5p)² + (2)² + 2(5p)(2)
= 25p² + 4 + 20p
So, (5p + 2)² = 25p² + 4 + 20p
Question 7.
(-7t + 4)2
Answer:
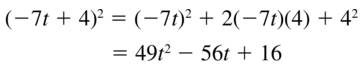
Question 8.
(-12 – n)2
Answer:
It is in the form of (a – b)² = a² + b² – 2ab
(-12 – n)² = (-12)² + n² – 2(-12)n
= 144 + n² + 24n
So, (-12 – n)² = 144 + n² + 24n
Question 9.
(2a + b)2
Answer:
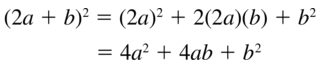
Question 10.
(6x – 3y)2
Answer:
(6x – 3y)2
It is in the form of (a – b)² = a² + b² – 2ab
(6x – 3y)² = (6x)² + (3y)² – 2(6x)(3y)
= 36x² + 9y² – 36xy
So, (6x – 3y)² = 36x² + 9y² – 36xy
MATHEMATICAL CONNECTIONS In Exercises 11–14, write a polynomial that represents the area of the square.
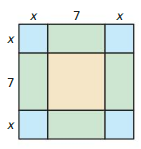
Question 11.
Answer:
Question 12.
Answer:
(x + x + 7)(x + x + 7) = (2x + 7)²
It is in the form of (a + b)² = a² + b² + 2ab
(2x + 7)² = (2x)² + 7² + 2(2x)(7)
= 4x² + 49 + 28x
(2x + 7)² = 4x² + 49 + 28x
Question 13.
Answer:
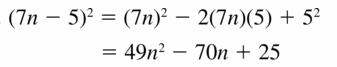
Question 14.
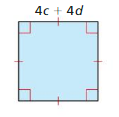
Answer:
A = s × s
A = (4c + 4d)(4c + 4d)
It is in the form of (a + b)² = a² + b² + 2ab
(4c + 4d)² = (4c)² + (4d)² + 2(4c)(4d)
= 16c² + 16d² + 32cd
(4c + 4d)² = 16c² + 16d² + 32cd
In Exercises 15–24, find the product.
Question 15.
(t – 7)(t + 7)
Answer:
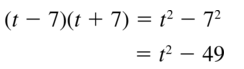
Question 16.
(m + 6)(m – 6)
Answer:
(m + 6)(m – 6)
It is in the form of (a + b)(a – b) = a² – b²
(m + 6)(m – 6) = m² – 6²
= m² – 36
Question 17.
(4x + 1)(4x – 1)
Answer:
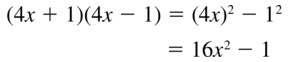
Question 18.
(2k – 4)(2k + 4)
Answer:
(2k – 4)(2k + 4)
It is in the form of (a + b)(a – b) = a² – b²
(2k – 4)(2k + 4) = (2k)² – (4)²
= 4k² – 16
Question 19.
(8 + 3a)(8 – 3a)
Answer:
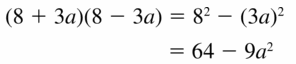
Question 20.
(\(\frac{1}{2}\) – c )(\(\frac{1}{2}\) + c )
Answer:
(\(\frac{1}{2}\) – c )(\(\frac{1}{2}\) + c )
It is in the form of (a + b)(a – b) = a² – b²
(\(\frac{1}{2}\) – c )(\(\frac{1}{2}\) + c ) = \(\frac{1}{2}\)² – c²
= \(\frac{1}{4}\) – c²
Question 21.
(p – 10q)(p + 10q)
Answer:
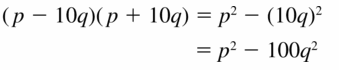
Question 22.
(7m + 8n)(7m – 8n)
Answer:
(7m + 8n)(7m – 8n)
It is in the form of (a + b)(a – b) = a² – b²
(7m + 8n)(7m – 8n) = (7m)² – (8n)²
49m² – 64n²
Question 23.
(-y + 4)(-y – 4)
Answer:
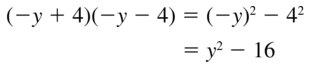
Question 24.
(-5g – 2h)(-5g + 2h)
Answer:
(-5g – 2h)(-5g + 2h)
It is in the form of (a + b)(a – b) = a² – b²
(-5g – 2h)(-5g + 2h) = (-5g)² – (2h)²
= 25g² – 4h²
In Exercises 25–30, use special product patterns to find the product.
Question 25.
16 • 24
Answer:
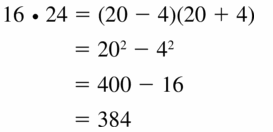
Question 26.
33 • 27
Answer:
33 • 27 = (30 + 3)(30 – 3)
It is in the form of (a + b)(a – b) = a² – b²
(30 + 3)(30 – 3) = 30² – 3²
= 900 – 9
= 891
Question 27.
422
Answer:
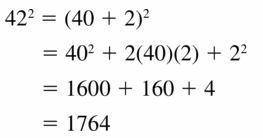
Question 28.
292
Answer:
29² = (30 – 1)²
It is in the form of (a – b)² = a² + b² – 2ab
(30 – 1)² = 30² + 1² – 2(30)(1)
= 900 + 1 – 60
= 841
Question 29.
30.52
Answer:
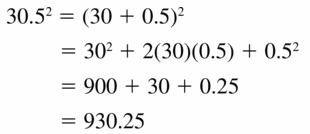
Question 30.
10\(\frac{1}{3}\) • 9\(\frac{2}{3}\)
Answer:
(10 – \(\frac{1}{3}\))(10 + \(\frac{1}{3}\))
It is in the form of (a + b)(a – b) = a² – b²
(10 – \(\frac{1}{3}\))(10 + \(\frac{1}{3}\)) = 10² – \(\frac{1}{3}\)²
= 100 – \(\frac{1}{9}\)
ERROR ANALYSIS In Exercises 31 and 32, describe and correct the error in finding the product.
Question 31.
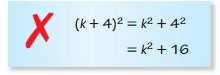
Answer:
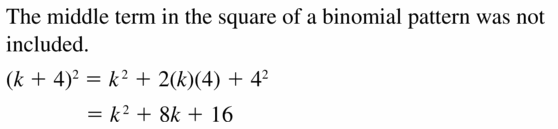
Question 32.
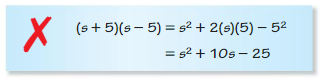
Answer:
(s + 5)(s – 5)
It is in the form of (a + b)(a – b) = a² – b²
(s + 5)(s – 5) = s² – 5²
= s² – 25
Question 33.
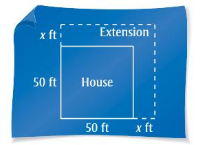
MODELING WITH MATHEMATICS
A contractor extends a house on two sides.
a. The area of the house after the renovation is represented by (x + 50)2. Find this product.
b. Use the polynomial in part (a) to fond the area when x = 15. What is the area of the extension?
Answer:

Question 34.
MODELING WITH MATHEMATICS
A square-shaped parking lot with 100-foot sides is reduced by x feet on one side and extended by x feet on an adjacent side.
a. The area of the new parking lot is represented by (100 – x)(100 + x). Find this product.
Answer:
(100 – x)(100 + x)
It is in the form of (a + b)(a – b) = a² – b²
(100 – x)(100 + x) = 100² – x²
= 10000 – x²
b. Does the area of the parking lot increase, decrease, or stay the same? Explain.
Answer:
The original area is 100 × 100 = 10,000 sq. ft
The new area is 10,000 – (10000 – x²) – x²
So, the area of the parking lot decreases and decreased by x²
c. Use the polynomial in part (a) to find the area of the new parking lot when x = 21.
Answer:
when x = 21
10000 – x²
= 10000 – 21²
= 10,000 – 441
= 9559 sq. ft
Question 35.
MODELING WITH MATHEMATICS
In deer, the gene N is for normal coloring and the gene a is for no coloring, or albino. Any gene combination with an N results in normal coloring. The Punnett square shows the possible gene combinations of an offspring and the resulting colors from parents that both have the gene combination Na.
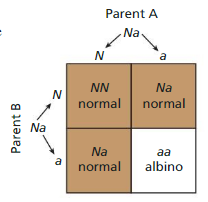
a. What percent of the possible gene combinations result in albino coloring?
b. Show how you could use a polynomial to model the possible gene combinations of the offspring.
Answer:

Question 36.
MODELING WITH MATHEMATICS
Your iris controls the amount of light that enters your eye by changing the size of your pupil.
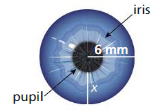
a. Write a polynomial that represents the area of your pupil. Write your answer in terms of π.
Answer:
r = 6 – x
A = π(6 – x)²
It is in the form of (a – b)² = a² + b² – 2ab
A = π(6² + x² – 2.6(x))
A = π(36 + x² – 12x)
A = π(x² – 12x + 36)
b. The width x of your iris decreases from 4millimeters to 2 millimeters when you enter a dark room. How many times greater is the area of your pupil after entering the room than before entering the room? Explain.
Answer:
Given,
The width x of your iris decreases from 4millimeters to 2 millimeters when you enter a dark room.
Area after entering/Area before entering = π(2² – 12(2) + 36)/π(4² – 12(4) + 36)
= 16π/4π
= 4
Question 37.
CRITICAL THINKING
Write two binomials that have the product x2 – 121. Explain.
Answer:

Question 38.
HOW DO YOU SEE IT?
In pea plants, any gene combination with a green gene (G) results in a green pod. The Punnett square shows the possible gene combinations of the offspring of two Gy pea plants and the resulting pod colors.
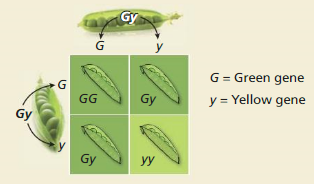
A polynomial that models the possible gene combinations of the offspring is
(0.5G + 0.5y)2 – 0.25G2 + 0.5Gy + 0.25y2.
Describe two ways to determine the percent of possible gene combinations that result in green pods.
Answer:
In Exercises 39–42, find the product.
Question 39.
(x2 + 1)(x2 – 1)
Answer:
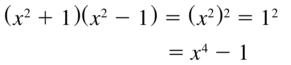
Question 40.
(y3 + 4)2
Answer:
(y3 + 4)²
It is in the form of (a + b)² = a² + b² + 2ab
(y3 + 4)² = (y³)² + 4² + 2y³(4)
= y6 + 16 + 8y³
Question 41.
(2m2 – 5n2)2
Answer:
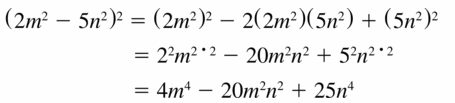
Question 42.
(r3 – 6t4)(r3 + 6t4)
Answer:
(r3 – 6t4)(r3 + 6t4)
It is in the form of (a + b)(a – b) = a² – b²
(r3 – 6t4)(r3 + 6t4) = (r3)² – (6t4)²
= r6 – 36t8
Question 43.
MAKING AN ARGUMENT
Your friend claims to be able to use a special product pattern to determine that (4\(\frac{1}{3}\))2 is equal to 16\(\frac{1}{9}\). Is your friend correct? Explain.
Answer:
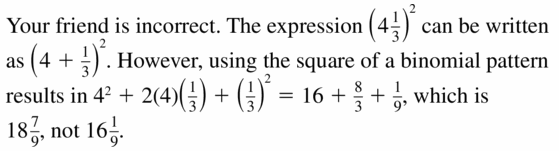
Question 44.
THOUGHT PROVOKING
The area (in square meters) of the surface of an artificial lake is represented by x2. Describe three ways to modify the dimensions of the lake so that the new area can be represented by the three types of special product patterns discussed in this section.
Answer:
Question 45.
REASONING
Find k so that 9x2 – 48x + k is the square of a binomial.
Answer:
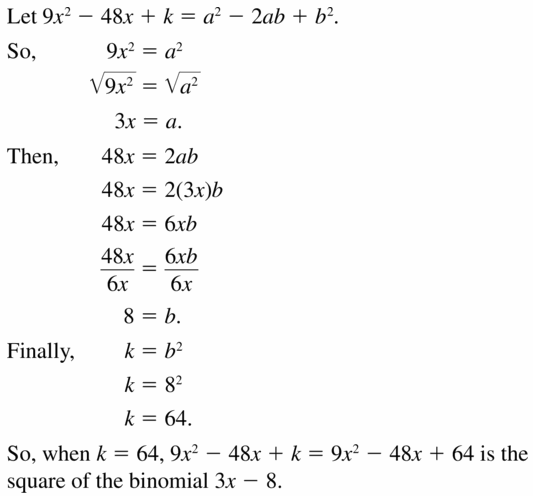
Question 46.
REPEATED REASONING
Find (x + 1)3 and (x + 2)3. Find a pattern in the terms and use it to write a pattern for the cube of a binomial (a + b)3.
Answer:
(x + 1)³ = (x)³ + (1)³ + 3(x)²(1) + 3(x)(1)²
x³ + 1 + 3x² + 3x
(x + 1)³ = x³ + 1 + 3x² + 3x
(x + 2)³ = (x)³ + (2)³ + 3(x)²(2) + 3(x)(2)²
x³ + 8 + 6x² + 12x
(x + 2)³ = x³ + 8 + 6x² + 12x
Question 47.
PROBLEM SOLVING
Find two numbers a and b such that (a + b)(a – b) < (a – b)2 < (a + b)2.
Answer:
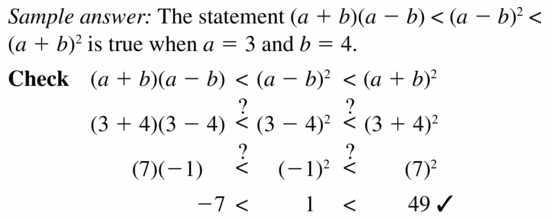
Maintaining Mathematical Proficiency
Factor the expression using the GCF.
Question 48.
12y – 18
Answer:
12y – 18 = 6(2y – 3)
Question 49.
9r + 27
Answer:
![]()
Question 50.
49s + 35t
Answer:
49s + 35t = 7(7s + 5t)
Question 51.
15x – 10y
Answer:
![]()
Lesson 7.4 Solving Polynomial Equations in Factored Form
Essential Question How can you solve a polynomial equation?
EXPLORATION 1
Matching Equivalent Forms of an Equation
Work with a partner. An equation is considered to be in factored form when the product of the factors is equal to 0. Match each factored form of the equation with its equivalent standard form and nonstandard form. Factored Form Standard Form Nonstandard Form

Answer:
a. (x – 1)(x – 3) = 0
x(x – 3) – 1(x – 3) = 0
x² – 3x – 1x + 3 = 0
x² – 4x + 3 = 0
a = C = 5
b. (x – 2)(x – 3) = 0
x(x – 3) – 2(x – 3) = 0
x² – 3x – 2x + 6 = 0
x² – 5x + 6 = 0
x² – 5x = -6
b = D = 1
c. (x + 1)(x – 2) = 0
x(x – 2) + 1(x – 2) = 0
x² – 2x + 1x – 2 = 0
x² – x – 2 = 0
c = A = 3
d. (x – 1)(x + 2) = 0
x(x + 2) – 1(x + 2) = 0
x² + 2x – 1x – 2 = 0
x² + x – 2 = 0
d = B = 4
e. (x + 1)(x – 3) = 0
x(x – 3) + 1(x – 3) = 0
x² – 3x + x – 3 = 0
x² – 2x – 3 = 0
e = E = 2
EXPLORATION 2
Writing a Conjecture

Work with a partner. Substitute 1, 2, 3, 4, 5, and 6 for x in each equation and determine whether the equation is true. Organize your results in a table. Write a conjecture describing what you discovered.
a. (x – 1)(x – 2) = 0
b. (x – 2)(x – 3) = 0
c. (x – 3)(x – 4) = 0
d. (x – 4)(x – 5) = 0
e. (x – 5)(x – 6) = 0
f. (x – 6)(x – 1) = 0
Answer:
a. (x – 1)(x – 2) = 0
x – 1 = 0 or x – 2 = 0
x = 1 or x = 2
x = 1, 2
b. (x – 2)(x – 3) = 0
x – 2 or x – 3 = 0
x = 2 or x = 3
x = 2, 3
c. (x – 3)(x – 4) = 0
x – 3 = 0 or x – 4 = 0
x = 3 or x = 4
x = 3, 4
d. (x – 4)(x – 5) = 0
x – 4 = 0 or x – 5 = 0
x = 4 or x = 5
x = 4, 5
e. (x – 5)(x – 6) = 0
x – 5 = 0 or x – 6 = 0
x = 5 or x = 6
x = 5, 6
f. (x – 6)(x – 1) = 0
x – 6 = 0 or x – 1 = 0
x = 6 or x = 1
x = 1, 6
EXPLORATION 3
Special Properties of 0 and 1
Work with a partner. The numbers 0 and 1 have special properties that are shared by no other numbers. For each of the following, decide whether the property is true for 0, 1, both, or neither. Explain your reasoning.
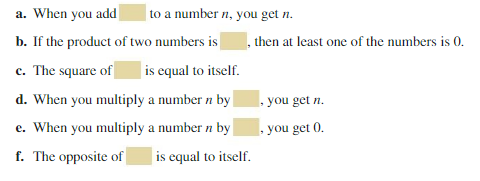
Answer:
a. When you add 0 to a number n, you get n.
b. If the product of two numbers is 0, then at least one of the numbers is 0.
c. The square of 1 is equal to itself.
d. When you multiply a number n by 1, you get n.
e. When you multiply a number n by 0, you get 0.
f. The opposite of 0 is equal to itself.
Communicate Your Answer
Question 4.
How can you solve a polynomial equation?
Answer:
Step 1: Write the equation in a correct form
Step 2: Use factoring strategies to factor in the problem.
Step 3: Use the zero product property and set each factor containing a variable equal to zero.
Step 4: Solve each factor that was set equal to zero by getting the x on one side and the answer on the other side.
Question 5.
One of the properties in Exploration 3 is called the Zero-Product Property. It is one of the most important properties in all of algebra. Which property is it? Why do you think it is called the Zero-Product Property? Explain how it is used in algebra and why it is so important.
Answer:
The most important property in all algebra is the Zero product property. The product of given numbers must be zero, so it is called zero product property. In algebra, for solving the equation having the expression equals zero, first we have to factor and use the zero product property to find the solutions.
Monitoring Progress
Solve the equation. Check your solutions.
Question 1.
x(x – 1) = 0
Answer:
x(x – 1) = 0
x = 0 or x – 1 = 0
x = 0 or x = 1
x = 0, 1
Question 2.
3t(t + 2) = 0
Answer:
3t(t + 2) = 0
3t = 0 or t + 2 = 0
t = 0 or t = -2
t = 0, -2
Question 3.
(z – 4)(z – 6) = 0
Answer:
(z – 4)(z – 6) = 0
z – 4 = 0 or z – 6 = 0
z = 4 or z = 6
z = 4, 6
Solve the equation. Check your solutions.
Question 4.
(3s + 5)(5s + 8) = 0
Answer:
(3s + 5)(5s + 8) = 0
3s + 5 = 0 or 5s + 8 = 0
3s = -5 or 5s = -8
s = -5/3 or s = -8/5
s = -5/3, -8/5
Question 5.
(b + 7)2 = 0
Answer:
(b + 7)2 = 0
squaring on both sides.
b + 7 = 0
b = -7
Question 6.
(d – 2)(d + 6)(d + 8) = 0
Answer:
(d – 2)(d + 6)(d + 8) = 0
d – 2 = 0 or d + 6 = 0 or d + 8 = 0
d = 2 or d = -6 or d = -8
d = 2, -6, -8
Question 7.
Factor out the greatest common monomial factor from 8y2 – 24y.
Answer:
8y2 – 24y = 8y(y – 3)
8y = 0 or y – 3 = 0
y = 0 or y = 3
y = 0, 3
Solve the equation. Check your solutions.
Question 8.
a2 + 5a = 0
Answer:
a2 + 5a = 0
a(a + 5) = 0
a = 0 or a + 5 = 0
a = 0 or a = -5
a = 0, -5
Question 9.
3s2 – 9s = 0
Answer:
3s2 – 9s = 0
3s(s – 3) = 0
3s = 0 or s – 3 = 0
s = 0 or s = 3
s = 0, 3
Question 10.
4x2 = 2x
Answer:
4x2 = 2x
2x(2x) = 2x
2x = 1
x = 1/2
Question 11.
You can model the entrance to a mine shaft using the equation y = – \(\frac{1}{2}\)(x + 4)(x – 4), where x and y are measured in feet. The x-axis represents the ground. Find the width of the entrance at ground level.
Answer:
You can model the entrance to a mine shaft using the equation y = – \(\frac{1}{2}\)(x + 4)(x – 4), where x and y are measured in feet.
y = – \(\frac{1}{2}\)(x + 4)(x – 4)
1/2 × 2 = -1
y = -1(x + 4)(x – 4)
x + 4 = 0 or x – 4 = 0
x = -4 or x = 4
4 – (-4) = 4 + 4 = 8 feet
width = 8 feet
Solving Polynomial Equations in Factored Form 7.4 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
Explain how to use the Zero-Product Property to find the solutions of the equation 3x(x – 6) = 0.
Answer:
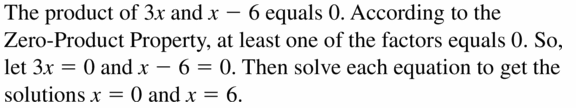
Question 2.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find both answers.

Answer:
Find the value of k for which
(2k + 4) + (k – 3) = 0
2k + 4 + k – 3 = 0
So, (2k + 4) + (k – 3) = 0 is different with others.
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, solve the equation.
Question 3.
x(x + 7) = 0
Answer:
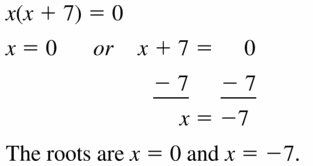
Question 4.
r(r – 10) = 0
Answer:
r(r – 10) = 0
r = 0 or r – 10 = 0
r = 0 or r = 10
r = 0, 10
Question 5.
12t(t – 5) = 0
Answer:
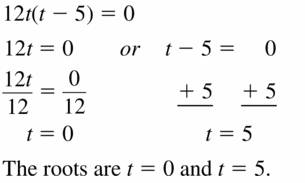
Question 6.
-2v(v + 1) = 0
Answer:
-2v(v + 1) = 0
-2v = 0 or v + 1 = 0
v = 0 or v = -1
v = 0, -1
Question 7.
(s – 9)(s – 1) = 0
Answer:
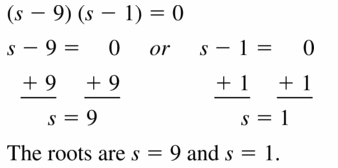
Question 8.
(y + 2)(y – 6) = 0
Answer:
(y + 2)(y – 6) = 0
y + 2 = 0 or y – 6 = 0
y = -2 or y = 6
y = -2, 6
In Exercises 9–20, solve the equation.
Question 9.
(2a – 6)(3a + 15) = 0
Answer:
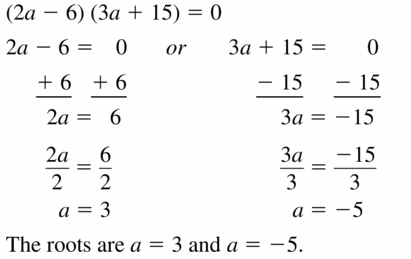
Question 10.
(4q + 3)(q + 2) = 0
Answer:
(4q + 3)(q + 2) = 0
4q + 3 = 0 or q + 2 = 0
4q = -3 or q = -2
q = -3/4 or q = -2
q = -3/4, -2
Question 11.
(5m + 4)2 = 0
Answer:

Question 12.
(h – 8)2 = 0
Answer:
(h – 8)2 = 0
Squaring on both sides
h – 8 = 0
h = 8
Question 13.
(3 – 2g)(7 – g) = 0
Answer:
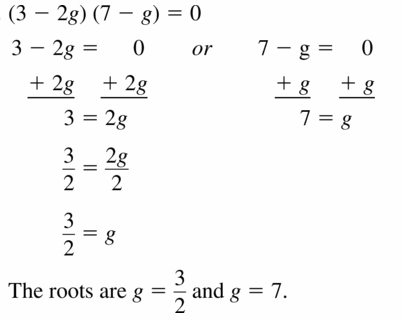
Question 14.
(2 – 4d )(2 + 4d ) = 0
Answer:
(2 – 4d )(2 + 4d ) = 0
2 – 4d = 0 or 2 + 4d = 0
2 = 4d or 2 = -4d
1 = 2d or 1 = -2d
d = 1/2 or d = -1/2
So, d = 1/2, -1/2
Question 15.
z(z + 2)(z – 1) = 0
Answer:
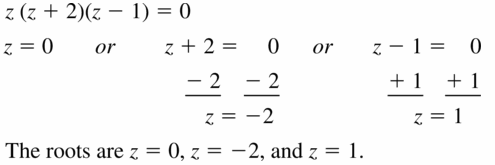
Question 16.
5p(2p – 3)(p + 7) = 0
Answer:
5p(2p – 3)(p + 7) = 0
5p = 0 or 2p – 3 = 0 or p + 7 = 0
p = 0 or p = 3/2 or p = -7
p = 0, 3/2, -7
Question 17.
(r – 4)2(r + 8) = 0
Answer:
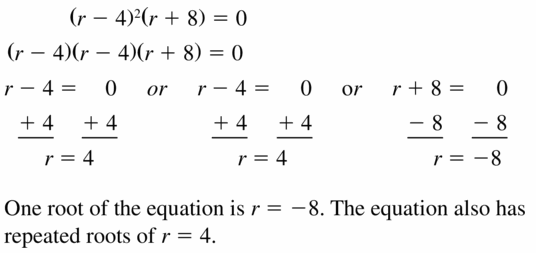
Question 18.
w(w – 6)2 = 0
Answer:
w(w – 6)2 = 0
w = 0 or (w – 6)² = 0
w = 0 or w – 6 = 0
w = 0 or w = 6
w = 0, 6
Question 19.
(15 – 5c)(5c + 5)(-c + 6) = 0
Answer:
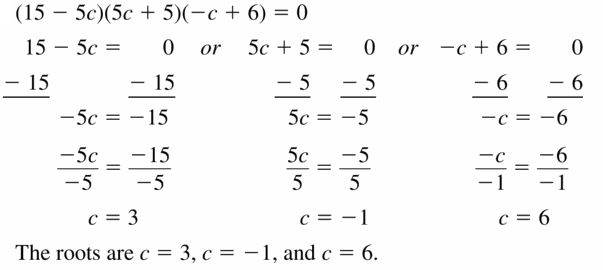
Question 20.
(2 – n) ( 6 + \(\frac{2}{3}\)n ) (n – 2) = 0
Answer:
(2 – n) ( 6 + \(\frac{2}{3}\)n ) (n – 2) = 0
2 – n = 0 or 6 + \(\frac{2}{3}\)n = 0 or n – 2 = 0
n = 2 or \(\frac{2}{3}\)n = -6 or n = 2
n = 2 or n = -18/2 or n = 2
n = 2 or n = -9 or n = 2
n = 2, -9
In Exercises 21–24, find the x-coordinates of the points where the graph crosses the x-axis.
Question 21.
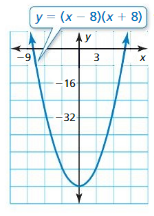
Answer:
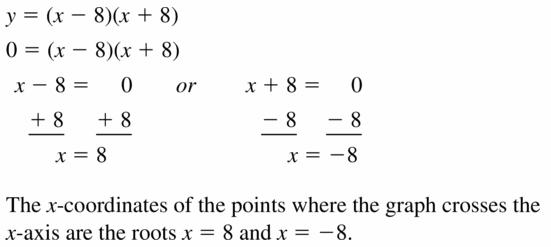
Question 22.
Answer:
y = (x + 1)(x + 7)
(x + 1)(x + 7) = 0
x + 1 = 0 or x + 7 = 0
x = -1 or x = -7
x = -1, -7
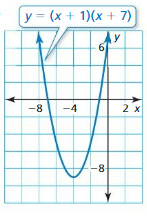
Question 23.
Answer:
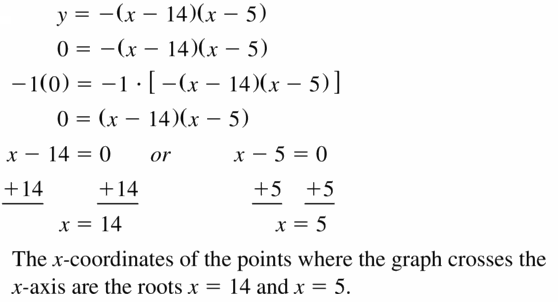
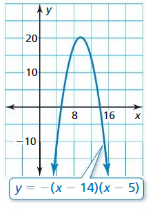
Question 24.
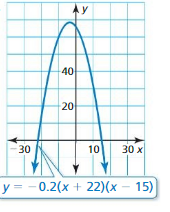
Answer:
y = -0.2(x + 22)(x – 15)
-0.2(x + 22)(x – 15) = 0
(x + 22)(x – 15) = 0
x + 22 = 0 or x – 15 = 0
x = -22 or x = 15
In Exercises 25–30, factor the polynomial.
Question 25.
5z2 + 45z
Answer:
![]()
Question 26.
6d2 – 21d
Answer:
6d2 – 21d = 3d(2d – 7)
Question 27.
3y3 – 9y2
Answer:
![]()
Question 28.
20x3 + 30x2
Answer:
20x3 + 30x² = 10x²(2x + 3)
Question 29.
5n6 + 2n5
Answer:
![]()
Question 30.
12a4 + 8a
Answer:
12a4 + 8a = 4a(3a³ + 2)
In Exercises 31–36, solve the equation.
Question 31.
4p2 – p = 0
Answer:
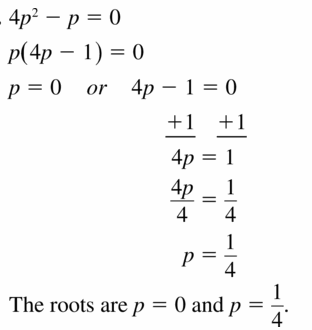
Question 32.
6m2 + 12m = 0
Answer:
6m2 + 12m = 0
6m(m + 2) = 0
6m = 0 or m + 2 = 0
m = 0 or m = -2
m = 0, -2
Question 33.
25c + 10c2 = 0
Answer:
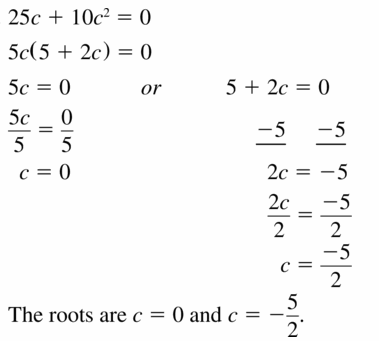
Question 34.
18q – 2q2 = 0
Answer:
2q(9 – q) = 0
2q = 0 or 9 – q = 0
q = 0 or 9 = q
q = 0, 9
Question 35.
3n2 = 9n
Answer:
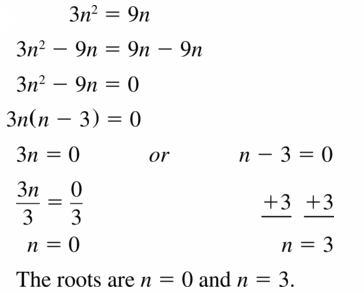
Question 36.
-28r = 4r2
Answer:
-28r = 4r2
4r² + 28r = 0
4r(r + 7) = 0
4r = 0 or r + 7 = 0
r = 0 or r = -7
Question 37.
ERROR ANALYSIS
Describe and correct the error in solving the equation.

Answer:
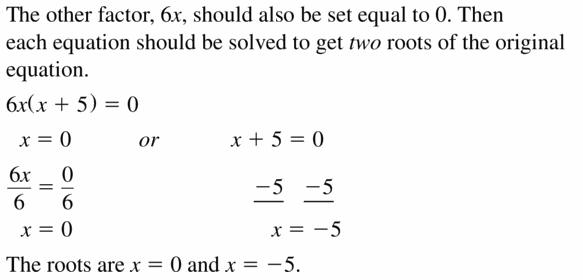
Question 38.
ERROR ANALYSIS
Describe and correct the error in solving the equation.

Answer:
3y² = 21y
Take 3y as common and cancel them.
y = 7
So, y = 7 is the solution.
Question 39.
MODELING WITH MATHEMATICS
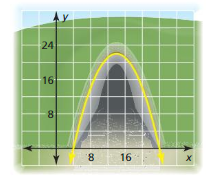
The entrance of a tunnel can be modeled by y = – \(\frac{11}{50}\)(x – 4)(x – 24), where x and y are measured in feet. The x-axis represents the ground. Find the width of the tunnel at ground level.
Answer:

Question 40.
MODELING WITH MATHEMATICS
The Gateway Arch in St. Louis can be modeled by y = – \(\frac{2}{315}\)(x + 315)(x – 315), where x and y are measured in feet. The x-axis represents the ground.
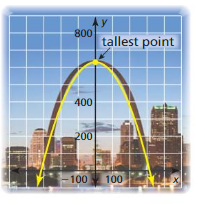
a. Find the width of the arch at ground level.
b. How tall is the arch?
Answer:
y = – \(\frac{2}{315}\)(x + 315)(x – 315)
x-intercept are -315 and 315.
Width = 315 – (-315) = 315 + 315 = 630 feet
y = -2/315(x + 315)(x – 315)
= -2/315(x² – 315²)
= -2/315x² + 630
when x = 0, y = 630
Hence the height is 630 ft
Question 41.
MODELING WITH MATHEMATICS
A penguin leaps out of the water while swimming. This action is called porpoising. The height y (in feet) of a porpoising penguin can be modeled by y = -16x2 + 4.8x, where x is the time (in seconds) since the penguin leaped out of the water. Find the roots of the equation when y = 0. Explain what the roots mean in this situation.
Answer:

Question 42.
HOW DO YOU SEE IT?
Use the graph to fill in each blank in the equation with the symbol + or -. Explain your reasoning.
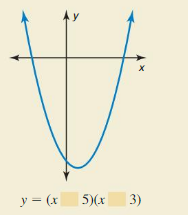
Answer:
When y = 0, (x – 5) or (x + 3)
x – 5 = 0 or x + 3 = 0
x = 5 or x = -3
y = (x – 5)(x + 3)
Question 43.
CRITICAL THINKING
How many x-intercepts does the graph of y = (2x + 5)(x – 9)2 have? Explain.
Answer:
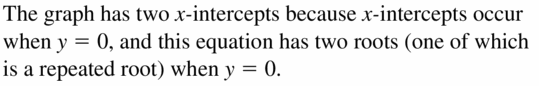
Question 44.
MAKING AN ARGUMENT
Your friend says that the graph of the equation y = (x – a)(x – b) always has two x-intercepts for any values of a and b. Is your friend correct? Explain.
Answer:
y = (x – a)(x – b)
(x – a)(x – b) = 0
x – a = 0 or x – b = 0
x = a or x = b
x = a, b
So, your friend is correct
Question 45.
CRITICAL THINKING
Does the equation (x2 + 3)(x4+ 1) = 0 have any real roots? Explain.
Answer:
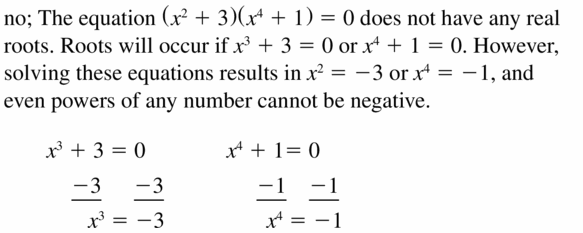
Question 46.
THOUGHT PROVOKING
Write a polynomial equation of degree 4 whose only roots are x = 1, x = 2, and x = 3.
Answer:
x = 1 = x – 1 = 0
x = 2 = x – 2 = 0
x = 3 = x – 3 = 0
x = 1 = x – 1 = 0
(x – 1)(x – 1)(x – 2)(x – 3) = 0
Question 47.
REASONING
Find the values of x in terms of y that are solutions of each equation.
a. (x + y)(2x – y) = 0
b. (x2 – y2)(4x + 16y) = 0
Answer:

Question 48.
PROBLEM SOLVING
Solve the equation (4x-5 – 16)(3x – 81) = 0.
Answer:
(4x-5 – 16)(3x – 81) = 0
(4x-5 – 16) = 0 or (3x – 81) = 0
4x-5 – 16 = 0 or 3x – 81 = 0
4x-5 – 4² = 0 or 3x – 9² = 0
4x-5 = 4² or 3x = 9²
When bases are equal powers should be equated
x – 5 = 2 or x = 2
x = 2 + 5 or x = 2
x = 7, 2
Maintaining Mathematical Proficiency
List the factor pairs of the number.
Question 49.
10
Answer:
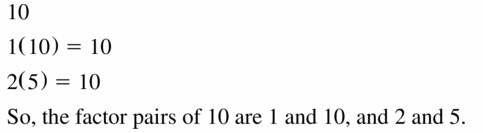
Question 50.
18
Answer:
The factor pairs of 18 are
1 × 18
2 × 9
3 × 6
So, the factor pairs of 18 are 1, 2, 3, 6, 9, 18.
Question 51.
30
Answer:

Question 52.
48
Answer:
48 = 1 × 48
2 × 24
3 × 16
4 × 12
6 × 8
So, the factor pairs of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48.
Polynomial Equations and Factoring Study Skills: Preparing for a Test
7.1–7.4 What Did You Learn?
Core Vocabulary

Core Concepts

Mathematical Practices
Question 1.
Explain how you wrote the polynomial in Exercise 11 on page 375. Is there another method you can use to write the same polynomial?
Answer:
Question 2.
Find a shortcut for exercises like Exercise 7 on page 381 when the variable has a coefficient of 1. Does your shortcut work when the coefficient is not 1?
Answer:
Study Skills: Preparing for a Test
- Review examples of each type of problem that could appear on the test.
- Review the homework problems your teacher assigned.
- Take a practice test

Polynomial Equations and Factoring 7.1–7.4 Quiz
Write the polynomial in standard form. Identify the degree and leading coefficient of the polynomial. Then classify the polynomial by the number of terms.
Question 1.
-8q3
Answer:
Given,
-8q³
The coefficient of the polynomial is -8
The degree of the polynomial is 3
Number of terms = 1
The name of the polynomial is monomial.
Question 2.
9 + d2 – 3d
Answer:
9 + d2 – 3d
The coefficient of the polynomial is 1, -3
The degree of the polynomial is 2
Number of terms = 3
The name of the polynomial is trinomial.
Question 3.
\(\frac{2}{3}\)m4 – \(\frac{5}{6}\)m6
Answer:
\(\frac{2}{3}\)m4 – \(\frac{5}{6}\)m6
The coefficient of the polynomial is \(\frac{2}{3}\), –\(\frac{5}{6}\)
The degree of the polynomial is 6
Number of terms = 2
The name of the polynomial is binomial.
Question 4.
-1.3z + 3z4 + 7.4z2
Answer:
-1.3z + 3z4 + 7.4z2
The coefficient of the polynomial is 3, 7.4, -1.3
The degree of the polynomial is 4
Number of terms = 3
The name of the polynomial is trinomial.
Find the sum or difference.
Question 5.
(2x2 + 5) + (-x2 + 4)
Answer:
(2x2 + 5) + (-x2 + 4)
2x2 + 5 – x2 + 4
x² + 5 + 4
x² + 9
(2x2 + 5) + (-x2 + 4) = x² + 9
Question 6.
(-3n2 + n) – (2n2 – 7)
Answer:
(-3n2 + n) – (2n2 – 7)
-3n2 + n – 2n2 + 7
-3n² + n – 7
(-3n2 + n) – (2n2 – 7) = -3n² + n – 7
Question 7.
(-p2 + 4p) – (p2 – 3p + 15)
Answer:
(-p2 + 4p) – (p2 – 3p + 15)
-p2 + 4p – p2 + 3p – 15
-2p² + 7p – 15
Question 8.
(a2 – 3ab + b2) + (-a2 + ab + b2)
Answer:
(a2 – 3ab + b2) + (-a2 + ab + b2)
a² – 3ab + b² – a² + ab + b²
-2ab + 2b²
(a2 – 3ab + b2) + (-a2 + ab + b2) = -2ab + 2b²
Find the product.
Question 9.
(w + 6)(w + 7)
Answer:
(w + 6)(w + 7)
w(w + 7) + 6(w + 7)
w² + 7w + 6w + 42
w² + 13w + 42
Question 10.
(3 – 4d )(2d – 5)
Answer:
(3 – 4d )(2d – 5)
3(2d – 5) – 4d(2d – 5)
6d – 15 – 8d² + 20d
-8d² + 26d – 15
Question 11.
(y + 9)(y2 + 2y – 3)
Answer:
(y + 9)(y2 + 2y – 3)
y(y2 + 2y – 3) + 9(y2 + 2y – 3)
y³ + 2y² – 3y + 9y² + 18y – 27
y³ + 11y² + 15y – 27
Question 12.
(3z – 5)(3z + 5)
Answer:
(3z – 5)(3z + 5)
It is in the form of (a + b)(a – b) = a² – b²
(3z – 5)(3z + 5) = (3z)² – (5)²
= 9z² – 25
Question 13.
(t + 5)2
Answer:
(t + 5)2
It is in the form of (a + b)² = a² + b² + 2ab
(t + 5)2 =t² + 5² + 2(t)(5)
= t² + 25 + 10t
Question 14.
(2q – 6)2
Answer:
(2q – 6)2
It is in the form of (a – b)² = a² + b² – 2ab
(2q – 6)² = (2q)² + 6² – 2(2q)(6)
= 4q² + 36 – 24q
Solve the equation.
Question 15.
5x2 – 15x = 0
Answer:
5x2 – 15x = 0
5x(x – 3) = 0
5x = 0 or x – 3 = 0
x = 0 or x = 3
x = 0, 3
Question 16.
(8 – g)(8 – g) = 0
Answer:
(8 – g)(8 – g) = 0
8 – g = 0 or 8 – g = 0
g = 8
Question 17.
(3p + 7)(3p – 7)( p + 8) = 0
Answer:
(3p + 7)(3p – 7)( p + 8) = 0
3p + 7 = 0 or 3p – 7 = 0 or p + 8 = 0
3p = -7 or 3p = 7 or p = -8
p = -7/3, 7/3, -8
Question 18.
-3y( y – 8)(2y + 1) = 0
Answer:
-3y( y – 8)(2y + 1) = 0
-3y = 0 or y – 8 = 0 or 2y + 1 = 0
y = 0 or y = 8 or y = -1/2
y = 0, 8, -1/2
Question 19.
You are making a blanket with a fringe border of equal width on each side.

a. Write a polynomial that represents the perimeter of the blanket including the fringe.
Answer:
Length = 72 + x + x
= 2x + 72
Width = 48 + x + x
= 2x + 48
P = 2(l + w)
P = 2(120 + 4x)
= 240 + 8x
P = 8x + 240 in.
b. Write a polynomial that represents the area of the blanket including the fringe.
Answer:
Length = 72 + x + x
= 2x + 72
Width = 48 + x + x
= 2x + 48
A = lw
A = (72 + 2x)(48 + 2x)
= 4x² + 120x + 3456
c. Find the perimeter and the area of the blanket including the fringe when the width of the fringe is 4 inches.
Answer:
l = 72 + 4 + 4 = 80 in.
w = 48 + 4 + 4 = 56 in.
P = 2(l + w) = 2(80 + 56) = 272 in.
A = lw = 80 × 56 = 4480 sq. in
Question 20.
You are saving money to buy an electric guitar. You deposit $1000 in an account that earns interest compounded annually. The expression 1000(1 + r )2 represents the balance after 2 years, where r is the annual interest rate in decimal form.
a. Write the polynomial in a standard form that represents the balance of your account after 2 years.
b. The interest rate is 3%. What is the balance of your account after 2 years?
c. The guitar costs $1100. Do you have enough money in your account after 3 years? Explain.
Answer:
You are saving money to buy an electric guitar. You deposit $1000 in an account that earns interest compounded annually.
The expression 1000(1 + r )2 represents the balance after 2 years, where r is the annual interest rate in decimal form.
A = P(1 + r/2)nt
A = 1000(1 + 0.03/1)2
A = 1000(1.03)²
A = P(1 + r/2)nt
A = 1000(1 + 0.03/1)3
A = 1000(1.03)²
1000(1² + 2r + r²)
1000(1 + 2r + r²)
1000 + 2000r + 1000r²
1000r² + 2000r + 1000
Question 21.
The front of a storage bunker can be modeled by y = – \(\frac{5}{216}\)(x – 72)(x + 72), where x and y are measured in inches. The x-axis represents the ground. Find the width of the bunker at ground level.
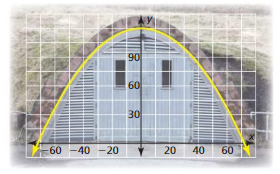
Answer:
y = – \(\frac{5}{216}\)(x – 72)(x + 72)
– \(\frac{5}{216}\)(x – 72)(x + 72) = 0
(x – 72)(x + 72) = 0
x – 72 = 0 or x + 72 = 0
x = 72 or x = -72
x = 72, -72
Lesson 7.5 Factoring x2 + bx + c
Essential Question How can you use algebra tiles to factor the trinomial x2 + bx + c into the product of two binomials?
EXPLORATION 1
Finding Binomial Factors
Work with a partner. Use algebra tiles to write each polynomial as the product of two binomials. Check your answer by multiplying.
Sample x2 + 5x + 6
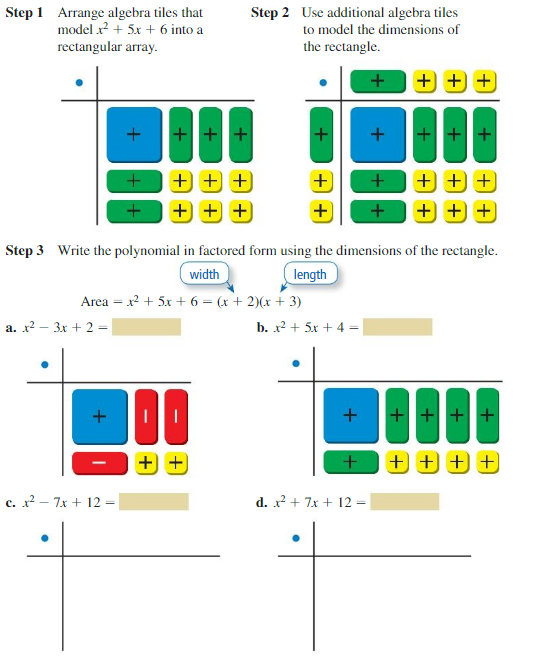
Answer:
a. x² – 3x + 2
2 × 1 = 2
x² – 1x – 2x + 2
x(x – 1) -2(x – 1)
(x – 1)(x – 2)
b. x² + 5x + 4
x² + 1x + 4x + 4
x(x + 1) + 4(x + 1)
(x + 1)(x + 4)
c. x² – 7x + 12
x² -4x – 3x + 12
x(x – 4) – 3(x – 4)
(x – 4)(x – 3)
d. x² + 7x + 12
x² + 4x + 3x + 12
x(x + 4) + 3(x + 4)
(x + 4)(x + 3)
Communicate Your Answer
Question 2.
How can you use algebra tiles to factor the trinomial x2 + bx + c into the product of two binomials?

Answer:
x2 + bx + c
1. Arrange algebra tiles for the given trinomial x2 + bx + c such that the model is a rectangular array.
2. Use additional algebra tiles to model the dimensions of the rectangle.
3. Write the polynomial in the factored form using the dimensions of the rectangle.
Question 3.
Describe a strategy for factoring the trinomial x2 + bx + c that does not use algebra tiles.
Answer:
Finding the factors of the polynomial x2 + bx + c.
Factor the polynomial.
Question 1.
x2 + 7x + 6
Answer:
x2 + 7x + 6
x² + 7x + 6
x² + 6x + 1x + 6
x(x + 6) + 1(x + 6)
(x + 6)(x + 1)
x + 6 = 0 or x + 1 = 0
x = -6, -1
Question 2.
x2 + 9x + 8
Answer:
x2 + 9x + 8
x² + 1x + 8x + 8
x(x + 1) + 8(x + 1)
(x + 1)(x + 8)
x + 1 = 0 or x + 8 = 0
x = -1 or x = -8
x = -1, -8
Factor the polynomial.
Question 3.
w2 – 4w + 3
Answer:
w2 – 4w + 3
w² – 1w – 3w + 3
w(w – 1) – 3(w – 1)
(w – 3)(w – 1)
w – 3 = 0 or w – 1 = 0
w = 3, 1
Question 4.
n2 – 12n + 35
Answer:
n2 – 12n + 35
n² – 7n – 5n + 35
n(n – 7) – 5(n – 7)
(n – 5)(n – 7)
n – 5 = 0 or n – 7 = 0
n = 5, 7
Question 5.
x2 – 14x + 24
Answer:
x2 – 14x + 24
x² – 12x – 2x + 24
x(x – 12) -2(x – 12)
(x – 12)(x – 2)
x = 2, 12
Question 6.
x2 + 2x – 15
Answer:
x2 + 2x – 15
x² + 5x – 3x – 15
x(x + 5) – 3(x + 5)
(x + 5)(x – 3)
x = 3, -5
Question 7.
y2 + 13y – 30
Answer:
y2 + 13y – 30
y² + 15y – 2y – 30
y(y + 15) – 2(y + 15)
(y + 15)(y – 2)
y = 2, -15
Question 8.
v2 – v – 42
Answer:
v2 – v – 42
v² – 7v + 6v – 42
v(v – 7) + 6(v – 7)
(v – 7)(v + 6)
v – 7 = 0 or v + 6 = 0
v = 7, -6
Question 9.
WHAT IF?
The area of the pumpkin patch is 200 square meters. What is the area of the square plot of land?
Answer:
Given,
The area of the pumpkin patch is 200 square meters.
The length of the pumpkin patch = (s – 40)
The width of the pumpkin batch = (s – 30)
A = lw
200 = (s – 40)(s – 30)
s² – 30s – 40s + 1200 = 200
s² – 70s + 1000 = 0
s² – 50s – 20s + 1000
s(s – 50) – 20(s – 50)
(s – 50)(s – 20) = 0
s – 50 = 0 or s – 20 = 0
s = 50 or 20
20 is less than 30 therefore the side of square is 50m.
Area of the plot = 50 × 50
= 2500 sq. meter
Factoring x2 + bx + c 7.5 Exercises
Vocabulary and Core Concept Check
Question 1.
WRITING
You are factoring x2 + 11x = 26. What do the signs of the terms tell you about the factors? Explain.
Answer:
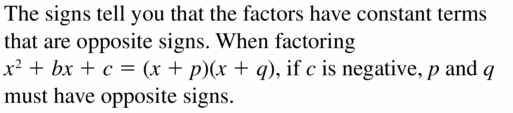
Question 2.
OPEN-ENDED
Write a trinomial that can be factored as (x + p)(x + q), where p and q are positive.
Answer:
(x + p)(x + q)
x² + px + qx + pq
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, factor the polynomial.
Question 3.
x2 + 8x + 7
Answer:

Question 4.
z2 + 10z + 21
Answer:
z2 + 7z + 3z + 21
z(z + 7) + 3(z + 7)
(z + 7)(z + 3)
z2 + 10z + 21 = (z + 7)(z + 3)
Question 5.
n2 + 9n + 20
Answer:
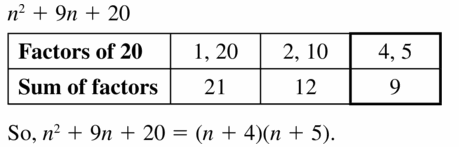
Question 6.
s2 + 11s + 30
Answer:
s2 + 11s + 30
s² + 6s + 5s + 30
s(s + 6) + 5(s + 6)
(s + 6)(s + 5)
s2 + 11s + 30 = (s + 6)(s + 5)
Question 7.
h2 + 11h + 18
Answer:
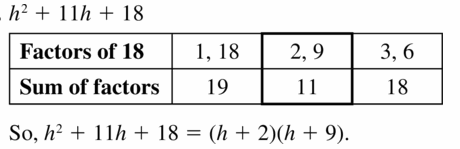
Question 8.
y2 + 13y + 40
Answer:
y2 + 13y + 40
y² + 8y + 5y + 40
y(y + 8) + 5(y + 8)
(y + 8)(y + 5)
y2 + 13y + 40 = (y + 8)(y + 5)
In Exercises 9–14, factor the polynomial.
Question 9.
v2 – 5v + 4
Answer:
Question 10.
x2 – 13x + 22
Answer:
x2 – 13x + 22
x² – 11x – 2x + 22
x(x – 11) -2(x – 11)
(x – 11)(x – 2)
x2 – 13x + 22 = (x – 11)(x – 2)
Question 11.
d2 – 5d + 6
Answer:
Question 12.
k2 – 10k + 24
Answer:
k2 – 10k + 24
k² – 6k – 4k + 24
k(k – 6) -4(k – 6)
(k – 6)(k – 4)
k2 – 10k + 24 = (k – 6)(k – 4)
Question 13.
w2 – 17w + 72
Answer:
Question 14.
j2 – 13j + 42
Answer:
j2 – 13j + 42
j² – 7j – 6j + 42
j(j – 7) -6(j – 7)
(j – 7)(j – 6)
j2 – 13j + 42 = (j – 7)(j – 6)
In Exercises 15–24, factor the polynomial.
Question 15.
x2 + 3x – 4
Answer:
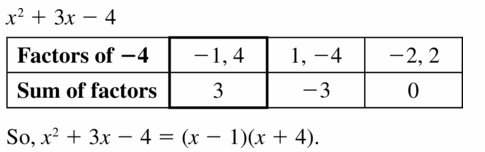
Question 16.
z2 + 7z – 18
Answer:
z2 + 7z – 18
z² + 9z – 2z – 18
z(z + 9) – 2(z + 9)
(z + 9)(z – 2)
z2 + 7z – 18 = (z + 9)(z – 2)
Question 17.
n2 + 4n – 12
Answer:

Question 18.
s2 + 3s – 40
Answer:
s2 + 3s – 40
s² + 8s – 5s – 40
s(s + 8) – 5(s + 8)
(s – 5)(s + 8)
s2 + 3s – 40 = (s – 5)(s + 8)
Question 19.
y2 + 2y – 48
Answer:
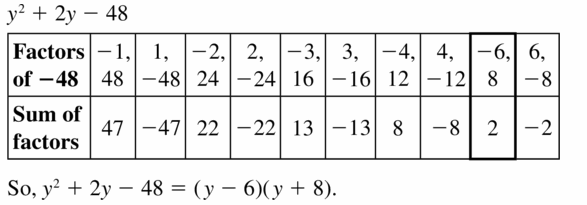
Question 20.
h2 + 6h – 27
Answer:
h2 + 6h – 27
h² + 9h – 3h – 27 = 0
h(h + 9) – 3(h + 9) = 0
(h + 9)(h – 3) = 0
h2 + 6h – 27 = (h + 9)(h – 3)
Question 21.
x2 – x – 20
Answer:
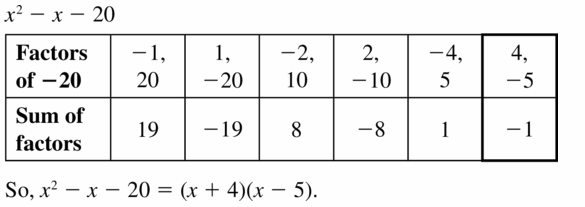
Question 22.
m2 – 6m – 7
Answer:
m2 – 6m – 7
m² – 7m + 1m – 7 = 0
m(m – 7) + 1(m – 7) = 0
(m – 7)(m + 1) = 0
m = 7, -1
Question 23.
-6t – 16 + t2
Answer:

Question 24.
-7y + y2 – 30
Answer:
-7y + y2 – 30
y² – 7y – 30 = 0
y² – 10y + 3y – 30 = 0
y(y – 10) + 3(y – 10) = 0
(y + 3)(y – 10) = 0
y = -3, 10
Question 25.
MODELING WITH MATHEMATICS
A projector displays an image on a wall. The area (in square feet) of the projection is represented by x2 – 8x + 15.
a. Write a binomial that represents the height of the projection.
b. Find the perimeter of the projection when the height of the wall is 8 feet.
Answer:

Question 26.
MODELING WITH MATHEMATICS
A dentist’s office and parking lot are on a rectangular piece of land. The area (in square meters) of the land is represented by x2 + x – 30.
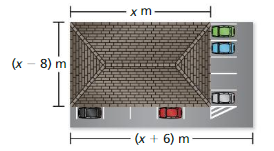
a. Write a binomial that represents the width of the land.
b. Find the area of the land when the length of the dentist’s office is 20 meters.
Answer:
x2 + x – 30
x² + 6x – 5x – 30 = 0
x(x + 6) – 5(x + 6) = 0
(x + 6)(x – 5) = 0
x = -6, 5
So, the factors (x + 6) and (x – 5) represent the length and width of the rectangular piece of land.
ERROR ANALYSIS In Exercises 27 and 28, describe and correct the error in factoring the polynomial.
Question 27.
Answer:

Question 28.
Answer:
s² – 17s – 60 = 0
s² – 20s + 3s – 60 = 0
s(s – 20) + 3(s – 20) = 0
(s – 20)(s + 3) = 0
s = -3, 20
In Exercises 29–38, solve the equation.
Question 29.
m2 + 3m + 2 = 0
Answer:
Question 30.
n2 – 9n + 18 = 0
Answer:
n2 – 9n + 18 = 0
n² – 6n – 3n + 18 = 0
n(n – 6) -3(n – 6) = 0
(n – 3)(n – 6) = 0
n = 3, 6
Question 31.
x2 + 5x – 14 = 0
Answer:
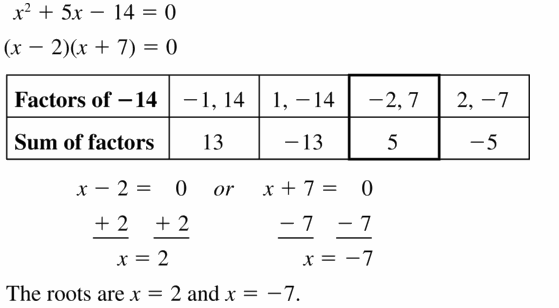
Question 32.
v2 + 11v – 26 = 0
Answer:
v2 + 11v – 26 = 0
v² + 13v – 2v – 26 = 0
v(v + 13) – 2(v + 13) = 0
(v + 13)(v – 2) = 0
v = -13, 2
Question 33.
t2 + 15t = -36
Answer:

Question 34.
n2 – 5n = 24
Answer:
n² – 5n = 24
n² – 5n – 24 = 0
n² – 8n + 3n – 24 = 0
n(n – 8) + 3(n – 8) = 0
(n – 8)(n + 3) = 0
n – 8 = 0 or n + 3 = 0
n = 8 or n = -3
n = -3, 8
Question 35.
a2 + 5a – 20 = 30
Answer:
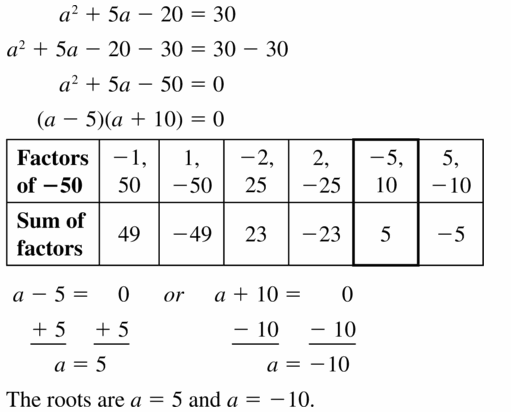
Question 36.
y2 – 2y – 8 = 7
Answer:
y2 – 2y – 8 = 7
y² – 2y – 8 – 7 = 0
y² – 2y – 15 = 0
y² – 5y + 3y – 15 = 0
y(y – 5) + 3(y – 5) = 0
(y – 5)(y + 3) = 0
y – 5 = 0 or y + 3 = 0
y = 5, -3
Question 37.
m2 + 10 = 15m – 34
Answer:

Question 38.
b2 + 5 = 8b – 10
Answer:
b2 + 5 = 8b – 10
b² + 5 – 8b + 10 = 0
b² – 8b + 15 = 0
b² – 3b – 5b + 15 = 0
b(b – 3) -5(b – 3) = 0
(b – 3)(b – 5)
b – 3 = 0 or b – 5 = 0
b = 3, 5
Question 39.
MODELING WITH MATHEMATICS
You trimmed a large square picture so that you could fit it into a frame. The area of the cut picture is 20 square inches. What is the area of the original picture?
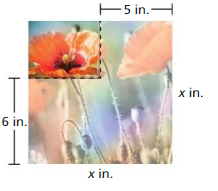
Answer:
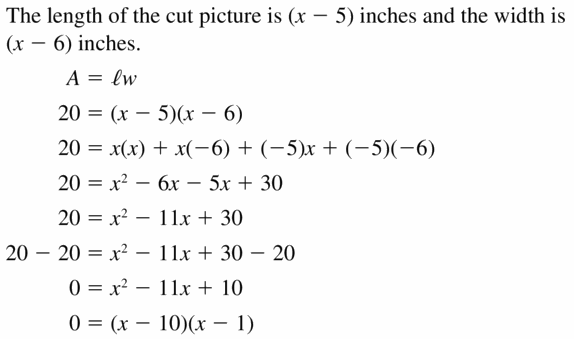

Question 40.
MODELING WITH MATHEMATICS
A web browser is open on your computer screen.
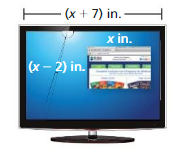
a. The area of the browser window is 24 square inches. Find the length of the browser window x.
b. The browser covers \(\frac{3}{13}\) of the screen. What are the dimensions of the screen?
Answer:
x² = 24 in²
x = √24 = 4.9 in.
A = \(\frac{3}{13}\) × 24 = 104 sq. in.
s\(\frac{3}{13}\) = 104 in\(\frac{3}{13}\)
s = √(104 in²) = 10.2 in.
Question 41.
MAKING AN ARGUMENT
Your friend says there are six integer values of b for which the trinomial x2 + bx – 12 has two binomial factors of the form (x + p) and (x + q). Is your friend correct? Explain.
Answer:

Question 42.
THOUGHT PROVOKING
Use algebra tiles to factor each polynomial modeled by the tiles. Show your work.
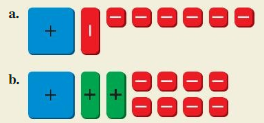
Answer:
a. x² – x – 6 = x² – 3x + 2x – 6
= x(x – 3) + 2(x – 3)
= (x + 2)(x – 3)
b. x² + 2x – 8
= x² + 4x – 2x – 8
= x(x + 4) – 2(x + 4)
= (x + 4)(x – 2)
MATHEMATICAL CONNECTIONS In Exercises 43 and 44, find the dimensions of the polygon with the given area.
Question 43.
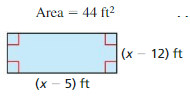
Answer:

Question 44.
Answer:
A = lw
35 = (g – 11)(g – 8)
35 = g(g – 8) – 11(g – 8)
35 = g² – 8g – 11g + 88
35 = g² – 19g + 88
g² – 19g + 88 – 35 = 0
g² – 19g + 53 = 0
Question 45.
REASONING
Write an equation of the form x2 + bx + c = 0 that has the solutions x = -4 and x = 6. Explain how you found your answer.
Answer:

Question 46.
HOW DO YOU SEE IT?
The graph of y = x2 + x – 6 is shown.
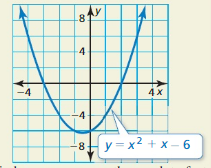
a. Explain how you can use the graph to factor the polynomial x2 + x – 6.
b. Factor the polynomial.
Answer:
x2 + x – 6
x² + 3x – 2x – 6
x(x + 3) – 2(x + 3)
(x + 3)(x – 2)
x = -3, 2
Question 47.
PROBLEM SOLVING
Road construction workers are paving the area shown.
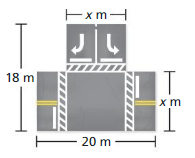
a. Write an expression that represents the area being paved.
b. The area being paved is 280 square meters. Write and solve an equation to find the width of the road x.
Answer:
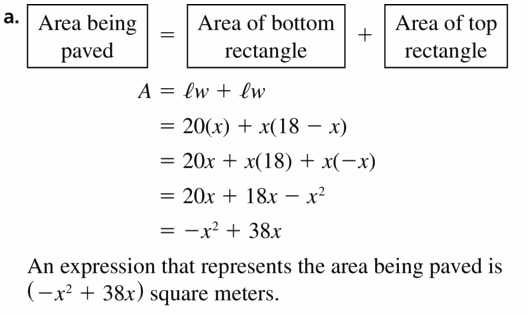
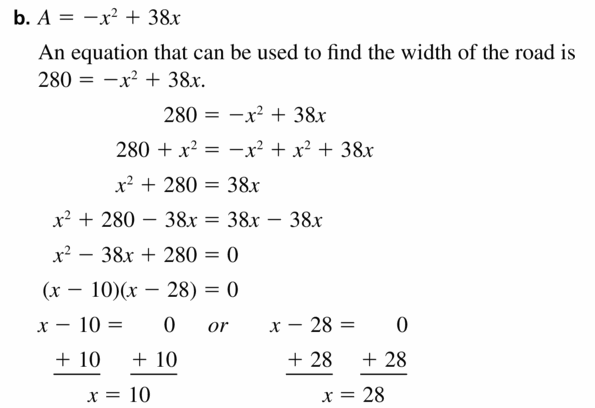

USING STRUCTURE In Exercises 48–51, factor the polynomial.
Question 48.
x2 + 6xy + 8y2
Answer:
x2 + 6xy + 8y²
x² + 4xy + 2xy + 4y²
x(x + 4y) + 2y(x + 4y)
(x + 4y)(x + 2y)
Question 49.
r2 + 7rs + 12s2
Answer:
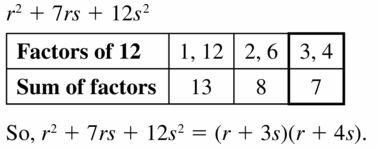
Question 50.
a2 + 11ab – 26b2
Answer:
a2 + 11ab – 26b2
Factors of 26 are (1, 26), (2, 13)
Sum of factors 13 – 2 = 11
a2 + 11ab – 26b²
= a² + 13ab – 2ab – 26b²
= a(a + 13b) – 2b(a + 13b)
= (a + 13b)(a – 2b)
Question 51.
x2 – 2xy – 35y2
Answer:
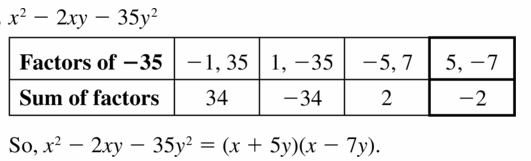
Maintaining Mathematical Proficiency
Solve the equation. Check your solution.
Question 52.
p – 9 = 0
Answer:
p – 9 = 0
p = 0 + 9
p = 9
So, the solution is p = 9.
Question 53.
z + 12 = -5
Answer:

Question 54.
6 = \(\frac{c}{-7}\)
Answer:
6 = \(\frac{c}{-7}\)
6 × -7 = c
c = -42
The solution is c = -42.
Question 55.
4k = 0
Answer:

Lesson 7.6 Factoring ax2 + bx + c
Essential Question How can you use algebra tiles to factor the trinomial ax2 + bx + c into the product of two binomials?
EXPLORATION 1
Finding Binomial Factors
Work with a partner. Use algebra tiles to write each polynomial as the product of two binomials. Check your answer by multiplying.
Sample 2x2 + 5x + 2
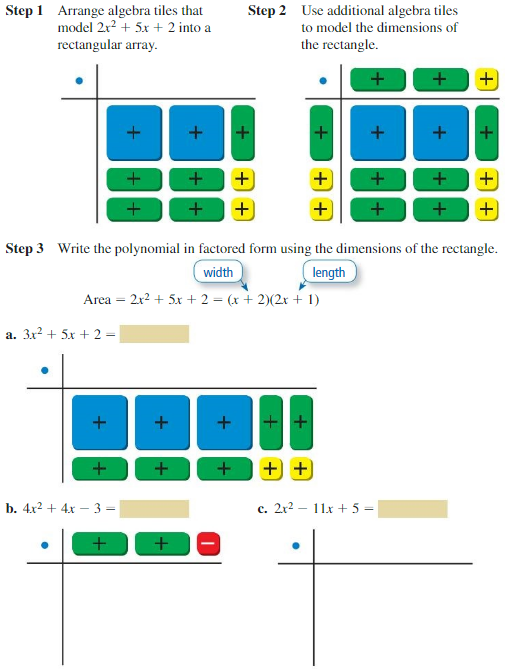
Answer:
a. 3x² + 5x + 2
3x² + 5x + 2 = 3x² + 3x + 2x + 2
= 3x(x + 1) + 2(x + 1)
= (x + 1)(3x + 2)
b. 4x² + 4x – 3 = (2x + 3)(2x – 1)
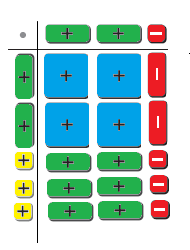
Check:
(2x + 3)(2x – 1) = 4x² – 2x + 6x – 3
= 4x² + 4x – 3
c.
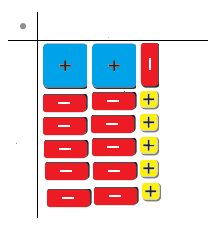
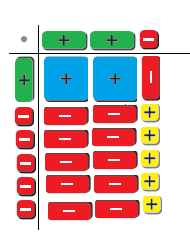
2x² – 11x + 5 = (x – 5)(2x – 1)
By checking
(x – 5)(2x – 1) = 2x² – x – 10x + 5
= 2x² – 11x + 5
Communicate Your Answer
Question 2.
How can you use algebra tiles to factor the trinomial ax2 + bx + c into the product of two binomials?

Answer:
If the value of c is negative, you would need zero pairs to model the factorization of the polynomial. The x-tiles on the board determine what the constants are in the factors. The product of these constants is equal to the value of c, so you would need positive tiles on one side of the x-squared tile and negative x-tiles on the other side to have opposite signs on the constants. Opposite signs on the constants will result in a negative value for c when multiplying the factors.
Question 3.
Is it possible to factor the trinomial 2x2 + 2x + 1? Explain your reasoning.
Answer:
No, it is not possible to factor the trinomial 2x2 + 2x + 1. Because it does not have the factors.
Monitoring Progress
Factor the polynomial.
Question 1.
8x2 – 56x + 48
Answer:
8x2 – 56x + 48
= 8(x² – 7x + 6)
= 8(x²- 1x – 6x + 6)
= 8[x(x – 1) – 6(x – 1)]
= 8[(x- 1)(x – 6)]
Question 2.
14x2 + 31x + 15
Answer:
14x2 + 31x + 15
14x² + 21x + 10x + 15
7x(2x + 3) + 5(2x + 3)
(7x + 5)(2x + 3)
Question 3.
2x2 – 7x + 5
Answer:
2x2 – 7x + 5
2x² – 2x – 5x + 5
2x(x – 1) -5(x – 1)
(x – 1)(2x – 5)
Question 4.
3x2 – 14x + 8
Answer:
3x2 – 14x + 8
3x² – 12x – 2x + 8
3x(x – 4) – 2(x – 4)
(x – 4)(3x – 2)
Question 5.
4x2 – 19x – 5
Answer:
4x2 – 19x – 5
4x² -20x + 1x – 5
4x(x – 5) + 1(x – 5)
(x – 5)(4x + 1)
Question 6.
6x2 + x – 12
Answer:
6x2 + x – 12
6x² + 9x – 8x – 12
3x(2x + 3) -4(2x + 3)
(2x + 3)(3x – 4)
Question 7.
-2y2 – 5y – 3
Answer:
-2y2 – 5y – 3
-2y² – 2y – 3y – 3
-2y(y + 1) – 3(y + 1)
(y + 1)(-2y – 3)
Question 8.
-5m2 + 6m – 1
Answer:
-5m2 + 6m – 1
-5m² + 5m + 1m – 1
-5m(m – 1) + 1(m – 1)
(m – 1)(-5m + 1)
Question 9.
-3x2 – x + 2
Answer:
-3x2 – x + 2
-3x² – 3x + 2x + 2
-3x(x + 1) + 2(x + 1)
(x + 1)(-3x + 2)
Question 10.
WHAT IF?
The area of the reserve is 136 square miles. How wide is the reserve?
Answer:
The area of the reserve is 136 square miles.
A = w(2w + 1)
136 = w(2w + 1)
2w² + w = 136
2w² + w – 136 = 0
2w² + 17w – 16w – 136 = 0
w(2w + 17) – 8(2w + 17) = 0
(w – 8)(2w + 17) = 0
w – 8 = 0 or 2w + 17 = 0
w = 8 or 2w = -17
w = 8 or w = -17/2
Thus the reserve is 8 miles wide.
Factoring ax2 + bx + c 7.6 Exercises
Vocabulary and Core Concept Check
Question 1.
REASONING
What is the greatest common factor of the terms of 3y2 – 21y + 36?
Answer:
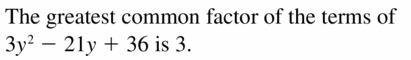
Question 2.
WRITING
Compare factoring 6x2 – x – 2 with factoring x2 – x – 2.
Answer:
6x2 – x – 2 = 6x² – 12x + 1x – 2
= 6x(x – 2) + 1(x – 2)
= (6x + 1)(x – 2)
x² – x – 2 = x² – 2x + 1x – 2
= x(x – 2) + 1(x – 2)
(x – 2)(x + 1)
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, factor the polynomial.
Question 3.
3x2 + 3x – 6
Answer:
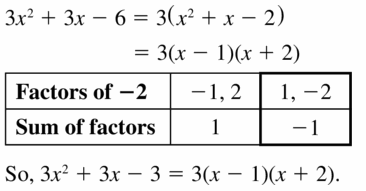
Question 4.
8v2 + 8v – 48
Answer:
8v² + 8v – 48
8(v² + v – 6)
8[v² + 3v – 2v – 6]
8[v(v + 3) – 2(v + 3)]
8[(v + 3)(v – 2)]
8v² + 8v – 48 = 8[(v + 3)(v – 2)]
Question 5.
4k2 + 28k + 48
Answer:
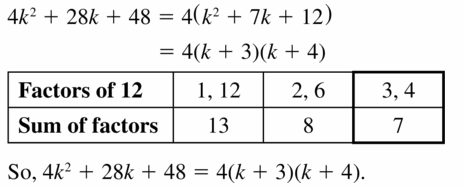
Question 6.
6y2 – 24y + 18
Answer:
6y² – 24y + 18
6[y² – 4y + 3]
= 6[y² – 3y – 1y + 3]
= 6[y(y – 3) – 1(y – 3)]
= 6[(y – 3) (y – 1)]
Question 7.
7b2 – 63b + 140
Answer:
Question 8.
9r2 – 36r – 45
Answer:
9r² – 36r – 45
= 9[r² – 4r – 5]
= 9[r² – 5r + 1r – 5]
= 9[r(r – 5) + 1(r – 5)]
= 9[(r – 5)(r + 1)]
In Exercises 9–16, factor the polynomial.
Question 9.
3h2 + 11h + 6
Answer:
Question 10.
8m2 + 30m + 7
Answer:
8m² + 30m + 7
= 8m² + 28m + 2m + 7
= 4m(2m + 7) + 1(2m + 7)
= (2m + 7)(4m + 1)
Question 11.
6x2 – 5x + 1
Answer:
Question 12.
10w2 – 31w + 15
Answer:
10w² – 31w + 15
10w² – 25w – 6w + 15
5w(2w – 5) – 3(2w – 5)
(2w – 5)(5w – 3)
10w² – 31w + 15 = (2w – 5)(5w – 3)
Question 13.
3n2 + 5n – 2
Answer:

Question 14.
4z2 + 4z – 3
Answer:
4z² + 4z – 3
4z² + 6z – 2z – 3
2z(2z + 3) – 1(2z + 3)
(2z – 1)(2x + 3)
Question 15.
8g2 – 10g – 12
Answer:
![]()
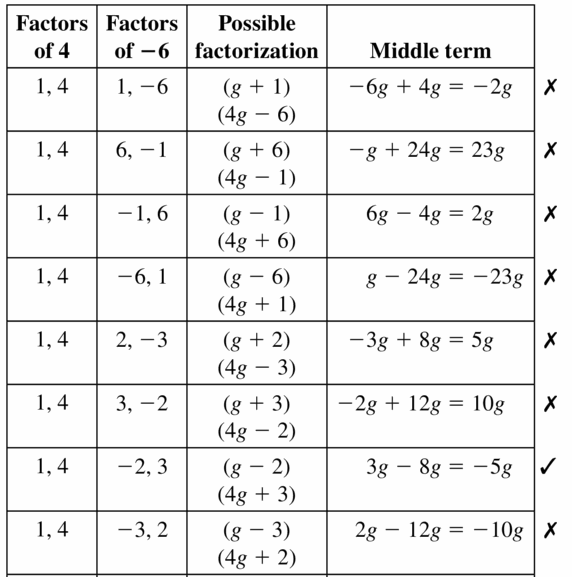
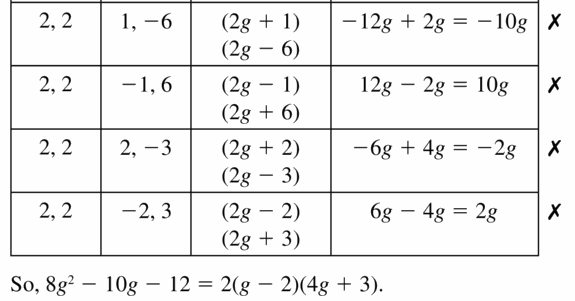
Question 16.
18v2 – 15v – 18
Answer:
18v² – 15v – 18
= 3(6v² – 5v – 6)
= 3[6v² – 9v + 4v – 6]
= 3[3v(2v – 3) + 2(2v – 3)]
= 3[(2v – 3)(3v + 2)]
In Exercises 17–22, factor the polynomial.
Question 17.
-3t2 + 11t – 6
Answer:
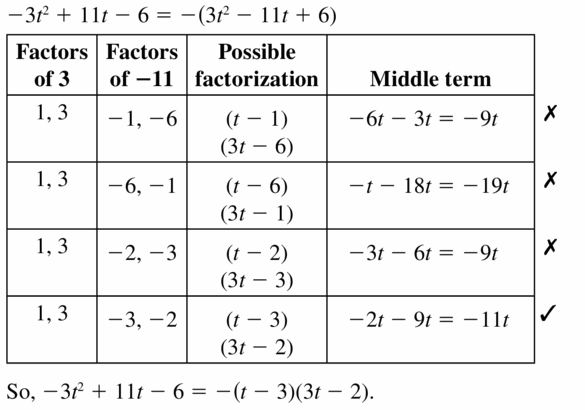
Question 18.
-7v2 – 25v – 12
Answer:
-7v² – 25v – 12
= -7v² – 7v – 12v – 12
= -7v(v + 1) – 12(v + 1)
= (v + 1)(-7v – 12)
Question 19.
-4c2 + 19c + 5
Answer:
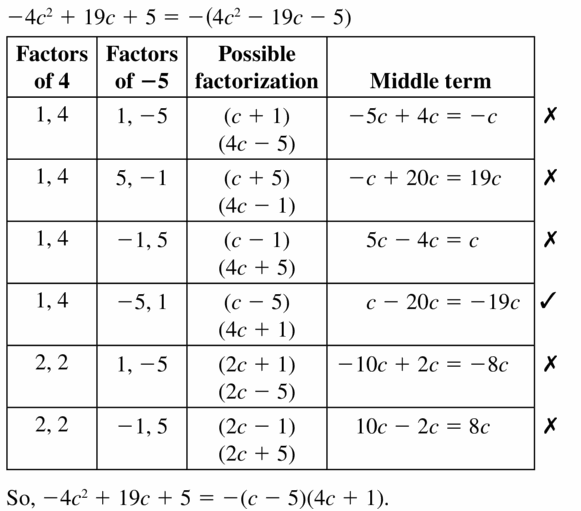
Question 20.
-8h2 – 13h + 6
Answer:
-8h² – 13n + 6
= -8h² – 16n + 3n + 6
= -8h(h + 2) + 3(h + 2)
= (h + 2)(-8h + 3)
Question 21.
-15w2 – w + 28
Answer:
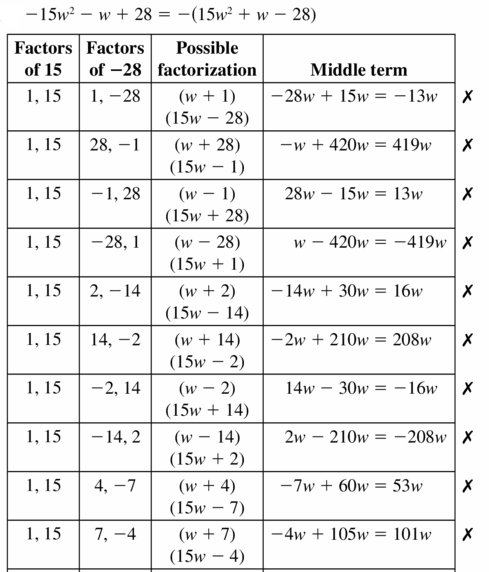


Question 22.
-22d2 + 29d – 9
Answer:
-22d² + 29d – 9
= -22d² + 11d + 18d – 9
= -11d(2d – 1) + 9(2d – 1)
= (-11d + 9)(2d – 1)
ERROR ANALYSIS In Exercises 23 and 24, describe and correct the error in factoring the polynomial.
Question 23.
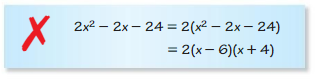
Answer:

Question 24.
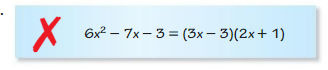
Answer:
6x² – 7x – 3
= 6x² – 9x + 2x – 3
= 3x(2x – 3) + 1(2x – 3)
= (2x – 3)(3x + 1)
In Exercises 25–28, solve the equation.
Question 25.
5x2 – 5x – 30 = 0
Answer:
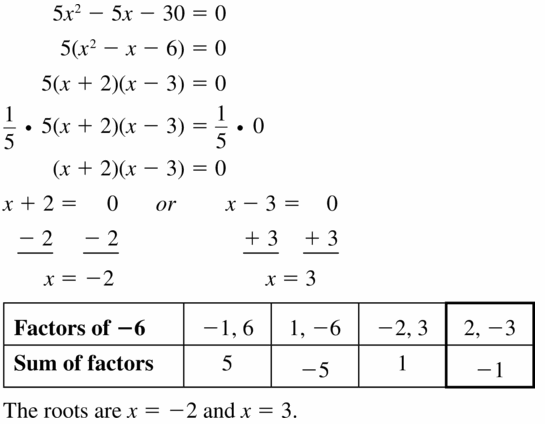
Question 26.
2k2 – 5k – 18 = 0
Answer:
2k² – 5k – 18 = 0
= 2k² + 4k – 9k – 18 = 0
= 2k(k + 2) – 9(k + 2) = 0
= (2k – 9)(k + 2) = 0
2k – 9 = 0 or k + 2 = 0
2k = 9 or k = -2
k = 9/2
k = 9/2, -2
Question 27.
-12n2 – 11n = -15
Answer:

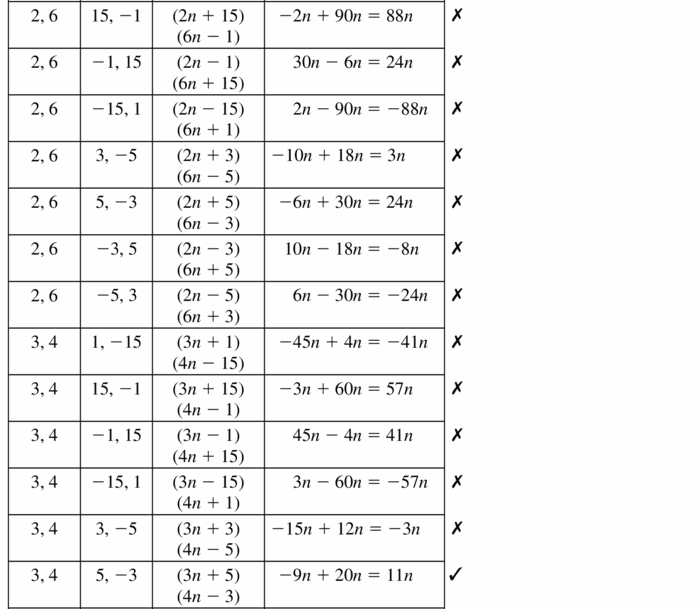

Question 28.
14b2 – 2 = -3b
Answer:
14b² – 2 = -3b
= 14b² – 2 + 3b = 0
= 14b² + 3b – 2 = 0
= 14b² + 7b – 4b – 2 = 0
= 7b(2b + 1) – 2(2b + 1) = 0
(2b + 1)(7b – 2) = 0
2b + 1 = 0 or 7b – 2 = 0
2b = -1 or 7b = 2
b = -1/2 or b = 2/7
b = -1/2, 2/7
In Exercises 29–32, find the x-coordinates of the points where the graph crosses the x-axis.
Question 29.
Answer:


Question 30.
Answer:
y = 4x² + 11x – 3
4x² + 11x – 3 = 0
4x² + 12x – 1x – 3 = 0
4x(x + 3) – 1(x + 3) = 0
(x + 3)(4x – 1) = 0
x + 3 = 0 or 4x – 1 = 0
x = -3 or x = 1/4
x = -3, 1/4
So, the solution is x = -3 and x = 1/4.
Question 31.
Answer:

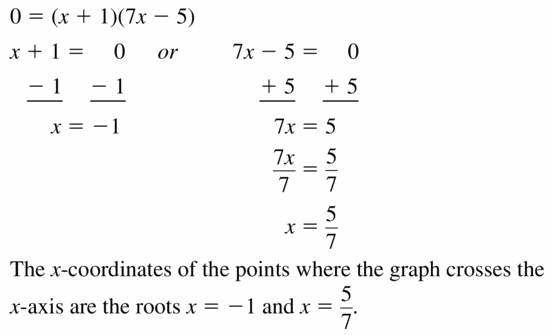
Question 32.
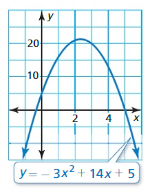
Answer:
y = -3x² + 14x + 5
= -3x² + 14x + 5 = 0
-3x² + 15x – 1x + 5 = 0
-3x(x – 5) -1(x – 5) = 0
(x – 5)(-3x – 1) = 0
x = 5, x = -1/3
So, the solution is x = 5 and x = 1/3
Question 33.
MODELING WITH MATHEMATICS
The area (in square feet) of the school sign can be represented by 15x2 – x – 2.
a. Write an expression that represents the length of the sign.
b. Describe two ways to find the area of the sign when x = 3.

Answer:

Question 34.
MODELING WITH MATHEMATICS
The height h (in feet) above the water of a cliff diver is modeled by h = -16t2 + 8t + 80, where t is the time (in seconds). How long is the diver in the air?
Answer:
Given,
The height h (in feet) above the water of a cliff diver is modeled by h = -16t2 + 8t + 80, where t is the time (in seconds).
h = -16t2 + 8t + 80
-16t2 + 8t + 80 = 0
8[-2t² + t + 10] = 0
-2t² + t + 10 = 0
-2t² + 5t – 4t + 10 = 0
-2t² – 4t + 5t + 10 = 0
-2t(t + 2) + 5(t + 2) = 0
(t + 2)(-2t + 5) = 0
t = -2 or t = 5/2
So, the t is 5/2.
Question 35.
MODELING WITH MATHEMATICS
The Parthenon in Athens, Greece, is an ancient structure that has a rectangular base. The length of the base of the Parthenon is 8 meters more than twice its width. The area of the base is about 2170 square meters. Find the length and width of the base.
Answer:


Question 36.
MODELING WITH MATHEMATICS
The length of a rectangular birthday party invitation is 1 inch less than twice its width. The area of the invitation is 15 square inches. Will the invitation fi t in the envelope shown without being folded? Explain.

Answer:
Given,
The length of a rectangular birthday party invitation is 1 inch less than twice its width.
The area of the invitation is 15 square inches.
Area = length × width
w = x
l = 2x – 1
A = 15 sq. in
x(2x – 1) = 15
2x² – x = 15
2x² – x – 15 = 0
2x² – 6x + 5x – 15 = 0
2x(x – 3) + 5(x – 3) = 0
(x – 3)(2x + 5) = 0
x = 3 or -5/2
x = 3 or -2.5
x = 3
w = 3
l = 2x – 1
l = 2(3) – 1 = 5
Question 37.
OPEN-ENDED
Write a binomial whose terms have a GCF of 3x.
Answer:
Question 38.
HOW DO YOU SEE IT?
Without factoring, determine which of the graphs represents the function g(x) = 21x2 + 37x + 12 and which represents the function h(x) = 21x2 – 37x + 12. Explain your reasoning.
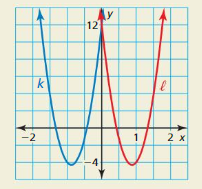
Answer:
Given,
g(x) = 21x2 + 37x + 12
h(x) = 21x2 – 37x + 12
Here c is positive
For g(x) the function has a positive value for b, the constant terms in each factor will both be positive which results in negative roots and the graph of the function g(x) = 21x2 + 37x + 12, has negative x-intercepts.
h(x) = 21x2 – 37x + 12 we have c is positive, the constant terms in each factor must have the same signs. The function has a negative value for b, the constant terms in each factor will both be negative which resulrs in positive roots and the graph of the function h(x) = 21x2 – 37x + 12 has two positive x-intercepts.
g(x) = 21x2 + 37x + 12
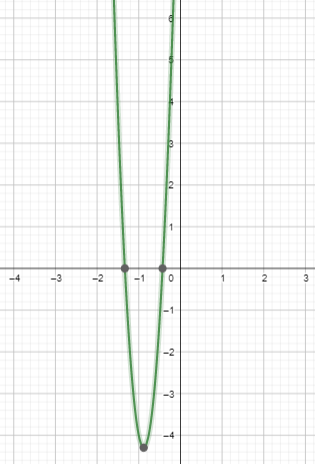
h(x) = 21x2 – 37x + 12
Question 39.
REASONING
When is it not possible to factor ax2 + bx + c, where a ≠ 1? Give an example.
Answer:
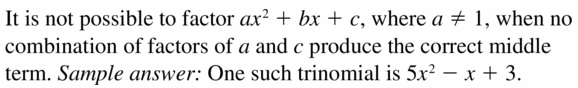
Question 40.
MAKING AN ARGUMENT
Your friend says that to solve the equation 5x2 + x – 4 = 2, you should start by factoring the left side as (5x – 4)(x + 1). Is your friend correct? Explain.
Answer:
5x2 + x – 4 = 2
5x² + x – 4 – 2 = 0
5x² + x – 6 = 0
5x² + 6x – 5x – 6 = 0
5x(x – 1) + 6(x – 1) = 0
(x – 1)(5x + 6) = 0
Your friend is not correct.
Question 41.
REASONING
For what values of t can 2x2 + tx + 10 be written as the product of two binomials?
Answer:
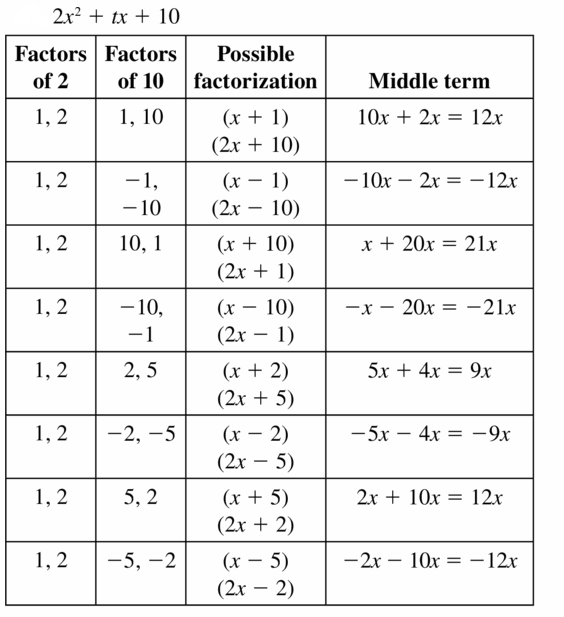
Question 42.
THOUGHT PROVOKING
Use algebra tiles to factor each polynomial modeled by the tiles. Show your work.
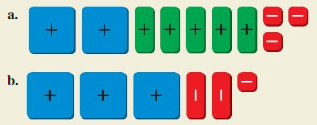
Answer:
a. 2x² + x +x + x + x + x – 1 – 1 – 1 = 2x² + 5x – 3
=2x² + 6x – 1x – 3
= 2x(x + 3) – 1(x + 1)
= (x + 3)(2x – 1)
b. 3x² – 2x – 1
3x² – 3x + 1x – 1
3x(x – 1) + 1(x – 1)
(x – 1)(3x + 1)
Question 43.
MATHEMATICAL CONNECTIONS
The length of a rectangle is 1 inch more than twice its width. The value of the area of the rectangle (in square inches) is 5 more than the value of the perimeter of the rectangle (in inches). Find the width.
Answer:


Question 44.
PROBLEM SOLVING
A rectangular swimming pool is bordered by a concrete patio. The width of the patio is the same on every side. The area of the surface of the pool is equal to the area of the patio. What is the width of the patio?
Answer:
l = 24 + 2x
w = 16 + 2x
A = (24 + 2x)(16 + 2x)
pool = patio
whole thing = twice pool
(24 + 2x)(16 + 2x) = 2(24)(16)
In Exercises 45–48, factor the polynomial.
Question 45.
4k2 + 7jk – 2j2
Answer:
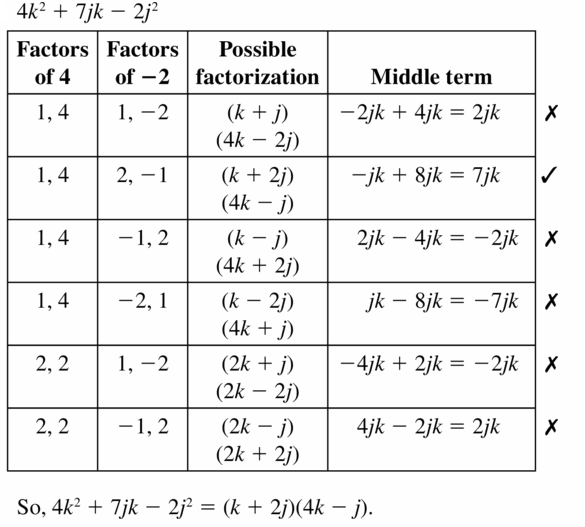
Question 46.
6x2 + 5xy – 4y2
Answer:
6x² + 5xy – 4y²
6x² – 3xy + 8xy – 4y²
3x(2x – y) + 4y(2x – y)
(3x + 4y)(2x – y)
Question 47.
-6a2 + 19ab – 14b2
Answer:

![]()
Question 48.
18m3 + 39m2n – 15mn2
Answer:
18m3 + 39m2n – 15mn²
3m(6m² + 13mn – 5n²)
3m(6m² + 10mn + 3mn – 5n²)
3m(3m(2m + n) – 5n(n + 2m))
3m(3m – 5n)(2m + n)
Maintaining Mathematical Proficiency
Find the square root(s).
Question 49.
± \(\sqrt{64}\)
Answer:
![]()
Question 50.
\(\sqrt{4}\)
Answer:
\(\sqrt{4}\) = ±2
Question 51.
– \(\sqrt{225}\)
Answer:
![]()
Question 52.
± \(\sqrt{81}\)
Answer:
± \(\sqrt{81}\) = 9
Solve the system of linear equations by substitution. Check your solution.
Question 53.
y = 3 + 7x
y – x = -3
Answer:
Question 54.
2x = y + 2
-x + 3y = 14
Answer:
2x = y + 2
-x + 3y = 14
x = 3y – 14
2(3y – 14) = y + 2
6y – 28 = y + 2
6y – y = 2 + 28
5y = 30
y = 30/5
y = 6
2x = y + 2
2x = 6 + 2
2x = 8
x = 8/2
x = 4
The solution is x = 4 and y = 6.
Question 55.
5x – 2y = 14
-7 = -2x + y
Answer:
Question 56.
-x – 8 = -y
9y – 12 + 3x = 0
Answer:
-x – 8 = -y ⇒ x + 8 = y
9y – 12 + 3x = 0
9(x + 8) – 12 + 3x = 0
9x + 72 – 12 + 3x = 0
12x + 60 = 0
12x = -60
x = -5
x + 8 = y
-5 + 8 = y
y = 3
Lesson 7.7 Factoring Special Products
Essential Question How can you recognize and factor special products?
EXPLORATION 1
Factoring Special Products Work with a partner. Use algebra tiles to write each polynomial as the product of two binomials. Check your answer by multiplying. State whether the product is a “special product” that you studied in Section 7.3.

Answer:
a. 4x² – 1 = (2x)² – (1)²
= (2x + 1)(2x – 1)
b. 4x² – 4x + 1
(a – b)²= a² + b² – 2ab
(2x – 1)² = (2x)² + (1)² – 2(2x)(1)
= 4x² + 1 – 4x
So, 4x² – 4x + 1 = (2x – 1)²
c. 4x² + 4x + 1
(a + b)²= a² + b² + 2ab
(2x – 1)² = (2x)² + (1)² + 2(2x)(1)
= 4x² + 1 + 4x
So, 4x² + 4x + 1 = (2x + 1)²
d. 4x² – 6x + 2
4x² – 4x – 2x + 2
4x(x – 1) – 1(x – 1)
(x – 1)(4x – 1)
4x² – 6x + 2 = (x – 1)(4x – 1)
EXPLORATION 2
Factoring Special Products
Work with a partner. Use algebra tiles to complete the rectangular array at the left in three different ways, so that each way represents a different special product. Write each special product in standard form and in factored form.
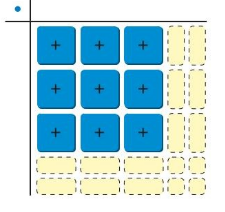
Communicate Your Answer
Question 3.
How can you recognize and factor special products? Describe a strategy for recognizing which polynomials can be factored as special products.
Answer: If there are only two terms then look for the sum of cubes or differences of squares or cubes. If there are three terms, look for squares of a difference or a sum. If there are three terms and the first coefficient is 1 then use simple trinomial factoring.
Question 4.
Use the strategy you described in Question 3 to factor each polynomial.
a. 25x2 + 10x + 1
b. 25x2 – 10x + 1
c. 25x2 – 1
Answer:
a. 25x2 + 10x + 1
25x² + 5x + 5x + 1
= 5x(5x + 1) + 1(5x + 1)
= (5x + 1)(5x + 1)
= (5x + 1)²
b. 25x2 – 10x + 1
25x² – 5x – 5x + 1
= 5x(5x – 1) -1(5x – 1)
= (5x – 1)(5x – 1)
= (5x – 1)²
c. 25x2 – 1
25x² – 1
(5x – 1)(5x + 1)
= (5x)² – 1²
Monitoring Progress
Factor the polynomial.
Question 1.
x2 – 36
Answer:
x2 – 36
It is in the form of a² – b²
x² – 36 can be written as x² – 6²
x² – 6² = (x + 6)(x – 6)
Question 2.
100 – m2
Answer:
100 – m²
It is in the form of a² – b²
10² – m² = (10 + m)(10 – m)
Question 3.
9n2 – 16
Answer:
9n² – 16
It is in the form of a² – b²
(3n)² – 4² = (3n + 4)(3n – 4)
Question 4.
16h2 – 49
Answer:
16h² – 49
It is in the form of a² – b²
16h² – 49 = (4h)² – 7² = (4h + 7)(4h – 7)
Use a special product pattern to evaluate the expression.
Question 5.
362 – 342
Answer:
36² – 34²
= (36 × 36) – (34 × 34)
= 1296 – 1156
= 140
Question 6.
472 – 442
Answer:
47² – 44²
= (47 × 47) – (44 × 44)
= 2209 – 1936
= 273
Question 7.
552 – 502
Answer:
55² – 50²
= (55 × 55) – (50 × 50)
= 3025 – 2500
= 525
Question 8.
282 – 242
Answer:
28² – 24²
= (28 × 28) – (24 × 24)
= 784 – 576
= 208
Factor the polynomial.
Question 9.
m2 – 2m + 1
Answer:
Given,
m² – 2m + 1
1 × 1 = 1
= m² – 1m – 1m + 1
= m(m – 1) – 1(m – 1)
= (m – 1)(m – 1)
Question 10.
d2 – 10d + 25
Answer:
d² – 10d + 25
5 × 5 = 25
5 + 5 = 10
d² – 5d – 5d + 25
d(d – 5) – 5(d – 5)
(d – 5)(d – 5)
Question 11.
9z2 + 36z + 36
Answer:
9z² + 36z + 36
9z² + 18z + 18z + 36
9z(z + 2) + 18(z + 2)
(z + 2)(9z + 18)
Solve the equation.
Question 12.
a2 + 6a + 9 = 0
Answer:
a² + 6a + 9 = 0
9 × 1 = 9
3 × 3 = 9
3 + 3 = 6
a² + 3a + 3a + 9 = 0
a(a + 3) + 3(a + 3) = 0
(a + 3)(a + 3) = 0
a + 3 = 0 or a + 3 = 0
a = -3, -3
Question 13.
w2 – \(\frac{7}{3}\)w + \(\frac{49}{36}\) = 0
Answer:
w² – \(\frac{7}{3}\)w + \(\frac{49}{36}\) = 0
It is in the form of (a – b)² = a² + b² – 2ab
w² – 2. \(\frac{7}{6}\)w + (\(\frac{7}{6}\))² = 0
(w – \(\frac{7}{6}\))² = 0
w – \(\frac{7}{6}\) = 0
w = \(\frac{7}{6}\)
Question 14.
n2 – 81 = 0
Answer:
n2 – 81 = 0
n² – 9² = 0
(n + 9)(n – 9) = 0
n = -9, 9
Question 15.
WHAT IF?
The golf ball does not hit the pine tree. After how many seconds does the ball hit the ground?
Answer:
Factoring Special Products 7.7 Exercises
Vocabulary and Core Concept Check
Question 1.
REASONING
Can you use the perfect square trinomial pattern to factor y2 + 16y + 64? Explain.
Answer:

Question 2.
WHICH ONE DOESN’T BELONG?
Which polynomial does not belong with the other three? Explain your reasoning.
![]()
Answer:
n² – 4 = (n + 4)(n – 4)
g² – 6g + 9 = (g – 3)²
r² + 12r + 36 = (r + 6)²
k² + 25 does not belong with the other three.
Monitoring Progress and Modeling with Mathematics
In Exercises 3–8, factor the polynomial.
Question 3.
m2 – 49
Answer:
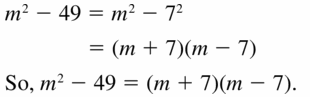
Question 4.
z2 – 81
Answer:
z² – 81 = z² – 9²
= (z + 9)(z – 9)
Question 5.
64 – 81d2
Answer:
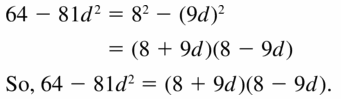
Question 6.
25 – 4x2
Answer:
25 – 4x²
= 5² – (2x)²
= (5 + 2x)(5 – 2x)
Question 7.
225a2 – 36b2
Answer:
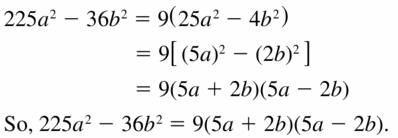
Question 8.
16x2 – 169y2
Answer:
16x² – 169y²
= (4x)² – (13y)²
= (4x + 13y)(4x – 13y)
In Exercises 9–14, use a special product pattern to evaluate the expression.
Question 9.
122 – 92
Answer:
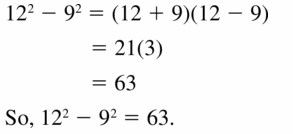
Question 10.
192 – 112
Answer:
19² – 11²
= (19 + 11)(19 – 11)
= 30 × 8
= 240
Question 11.
782 – 722
Answer:
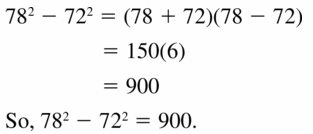
Question 12.
542 – 522
Answer:
54² – 52²
= (54 + 52)(54 – 52)
= (106)(2)
= 212
Question 13.
532 – 472
Answer:
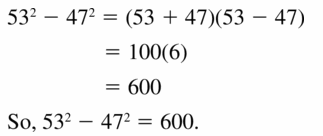
Question 14.
392 – 362
Answer:
39² – 36²
= (39 + 36)(39 – 36)
= (75)(3)
= 225
In Exercises 15–22, factor the polynomial.
Question 15.
h2 + 12h + 36
Answer:
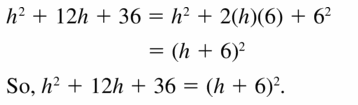
Question 16.
p2 + 30p + 225
Answer:
p² + 30p + 225
p² + 2(15)(p) + 15²
(p + 15)²
Question 17.
y2 – 22y + 121
Answer:
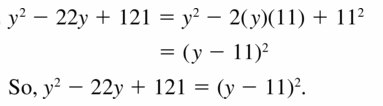
Question 18.
x2 – 4x + 4
Answer:
x² – 4x + 4
= x² – 2(2)x + 2²
= (x – 2)²
Question 19.
a2 – 28a + 196
Answer:
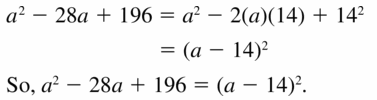
Question 20.
m2 + 24m + 144
Answer:
m² + 24m + 144
= m² + 2(12)m + 12²
= (m + 12)²
Question 21.
25n2 + 20n + 4
Answer:
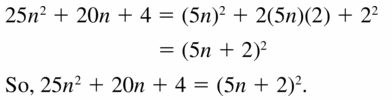
Question 22.
49a2 – 14a + 1
Answer:
49a² – 14a + 1
= (7a)² – 2(7)(a) + 1
= (7a – 1)²
ERROR ANALYSIS In Exercises 23 and 24, describe and correct the error in factoring the polynomial.
Question 23.
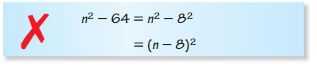
Answer:
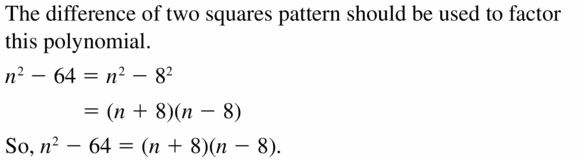
Question 24.
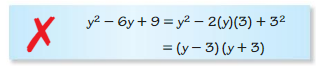
Answer:
y² – 6y + 9
= y² – 2(3)(y) + 3²
= (y – 3)²
Question 25.
MODELING WITH MATHEMATICS
The area (in square centimeters) of a square coaster can be represented by d2 + 8d + 16.

a. Write an expression that represents the side length of the coaster.
b. Write an expression for the perimeter of the coaster.
Answer:

Question 26.
MODELING WITH MATHEMATICS
The polynomial represents the area (in square feet) of the square playground.
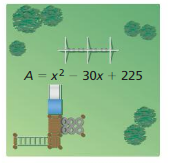
a. Write a polynomial that represents the side length of the playground.
b. Write an expression for the perimeter of the playground.
Answer:
A = x² – 30x + 225
A = x² – 2(15)x + 15²
A = (x – 15)²
s = x – 15
P = 4 × side
P = 4 × (x – 15)
P = 4x – 60
In Exercises 27–34, solve the equation.
Question 27.
z2 – 4 = 0
Answer:
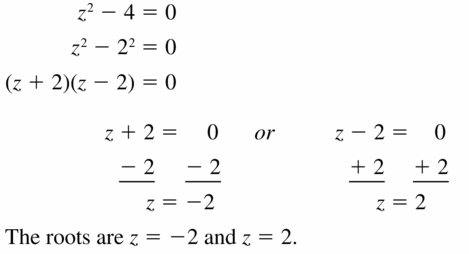
Question 28.
4x2 = 49
Answer:
4x² = 49
4x² – 49 = 0
(2x)² – 7² = 0
(2x + 7)(2x – 7) = 0
2x + 7 = 0 or 2x – 7 = 0
x = -7/2 or x = 7/2
x = -7/2, 7/2
Question 29.
k2 – 16k + 64 = 0
Answer:

Question 30.
s2 + 20s + 100 = 0
Answer:
s² + 20s + 100 = 0
s² + 2(10)(s) + 10² = 0
(s + 10)² = 0
s + 10 = 0
s = -10
Question 31.
n2 + 9 = 6n
Answer:
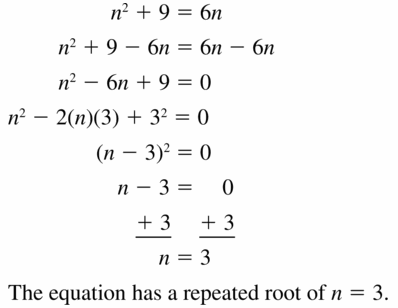
Question 32.
y2 = 12y – 36
Answer:
y² = 12y – 36
y² – 12y + 36 = 0
y² – 2(6)y + 6² = 0
(y – 6)² = 0
y – 6 = 0
y = 6
Question 33.
y2 + \(\frac{1}{2}\)y = – 1 — 16
Answer:
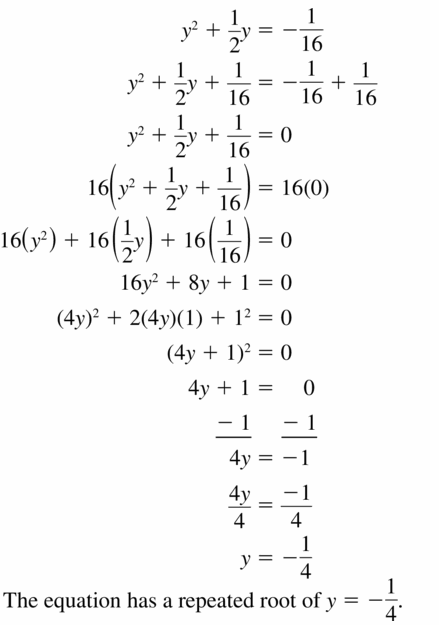
Question 34.
– \(\frac{4}{3}\)x + \(\frac{4}{9}\) = -x2
Answer:
– \(\frac{4}{3}\)x + \(\frac{4}{9}\) = -x2
x² – \(\frac{4}{3}\)x + \(\frac{4}{9}\) = 0
x² – 2(\(\frac{2}{3}\))x + \(\frac{2}{3}\)² = 0
(x – \(\frac{2}{3}\))² = 0
x – \(\frac{2}{3}\) = 0
x = \(\frac{2}{3}\)
In Exercises 35–40, factor the polynomial.
Question 35.
3z2 – 27
Answer:
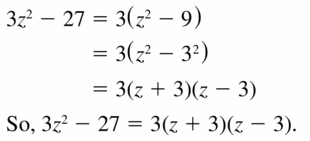
Question 36.
2m2 – 50
Answer:
2m2 – 50 = 2(m² – 25)
= 2(m + 5)(m – 5)
So, 2m2 – 50 = 2(m + 5)(m – 5)
Question 37.
4y2 – 16y + 16
Answer:
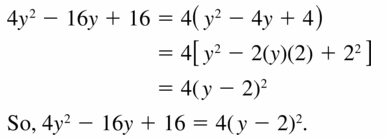
Question 38.
8k2 + 80k + 200
Answer:
8k2 + 80k + 200 = 8(k² + 10k + 25)
= 8(k² + 5k + 5k + 25)
= 8(k(k + 5) + 5(k + 5))
= 8(k + 5)(k + 5)
Question 39.
50y2 + 120y + 72
Answer:
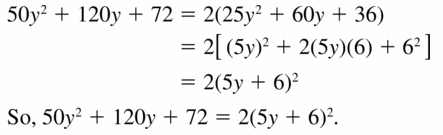
Question 40.
27m2 – 36m + 12
Answer:
27m2 – 36m + 12 = 3[9m² – 12m + 4]
= 3[9m² – 6m – 6m + 4]
= 3[3m(3m – 2) – 2(3m – 2)]
= 3[(3m – 2)(3m – 2)]
Question 41.
MODELING WITH MATHEMATICS
While standing on a ladder, you drop a paintbrush. The function represents the height y (in feet) of the paintbrush t seconds after it is dropped. After how many seconds does the paintbrush land on the ground?
Answer:
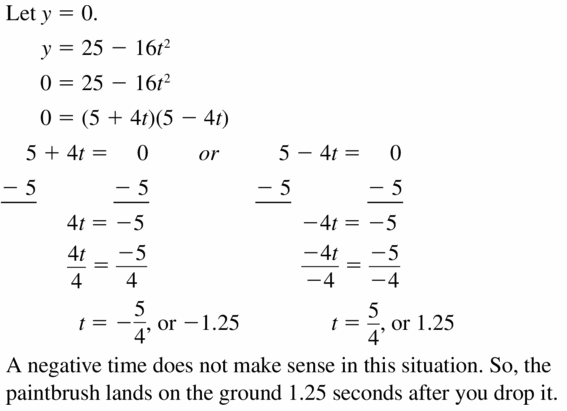
Question 42.
MODELING WITH MATHEMATICS
The function represents the height y (in feet) of a grasshopper jumping straight up from the ground t seconds after the start of the jump. After how many seconds is the grasshopper 1 foot off the ground?

Answer:
y = 1 foot
y = – 16t² + 8t
-16t² + 8t = 1
-16t² + 8t – 1 = 0
16t² – 8t + 1 = 0
(4t)² – 2(4t)(1) + 1² = 0
(4t – 1)² = 0
4t – 1 = 0
4t = 1
t = 1/4
t = 0.25 seconds
Question 43.
REASONING
Tell whether the polynomial can be factored. If not, change the constant term so that the polynomial is a perfect square trinomial.
a. w2 + 18w + 84
b. y2 – 10y + 23
Answer:


Question 44.
THOUGHT PROVOKING
Use algebra tiles to factor each polynomial modeled by the tiles. Show your work.
Answer:
a. 4x² – 1
= (2x)² – 1²
= (2x – 1)(2x + 1)
b. 4x² – 4x + 1
= 4x² – 2(2)(x) + 1²
= (2x)² – 2(2)x + 1²
= (2x – 1)²
Question 45.
COMPARING METHODS
Describe two methods you can use to simplify (2x – 5)2 – (x – 4)2. Which one would you use? Explain.
Answer:

Question 46.
HOW DO YOU SEE IT?
The figure shows a large square with an area of a2 that contains a smaller square with an area of b2.
a. Describe the regions that represent a2 – b2. How can you rearrange these regions to show that a2 – b2 = (a + b)(a – b)?
b. How can you use the figure to show that (a – b)2 = a2 – 2ab + b2?
Answer:
Question 47.
PROBLEM SOLVING
You hang nine identical square picture frames on a wall.
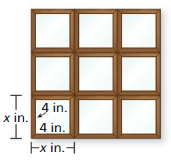
a. Write a polynomial that represents the area of the picture frames, not including the pictures.
b. The area in part (a) is 81 square inches. What is the side length of one of the picture frames? Explain your reasoning.
Answer:

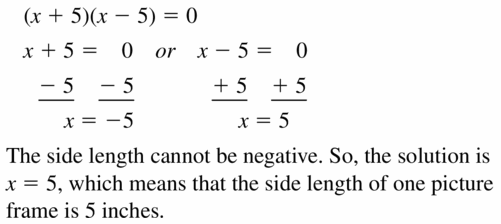
Question 48.
MATHEMATICAL CONNECTIONS
The composite solid is made up of a cube and a rectangular prism.
a. Write a polynomial that represents the volume of the composite solid.
b. The volume of the composite solid is equal to 25x. What is the value of x? Explain your reasoning.
Answer:
a. V = lbh
V = x × x × x
V = x³
Volume of the rectangular prism of length 4 inches, breadth x, and height 4 inches
V = 4 × 4 × x
V = 16x
V = x³ + 16x
b.
Given volume of the composite solid is 25x cu. units
V = x³ + 16x
x³ + 16x = 25x
x³ + 16x – 25x = 0
x³ – 9x = 0
x(x² – 9) = 0
x(x² – 3²) = 0
x(x + 3)(x – 3)
x = 0 or x + 3 = 0 or x – 3 = 0
x = 0, -3, 3
x = 3 in.
Maintaining Mathematical Proficiency
Write the prime factorization of the number.
Question 49.
50
Answer:
Question 50.
44
Answer:
The prime factorization of 44 are 2 × 2 × 11
Question 51.
85
Answer:

Question 52.
96
Answer:
The prime factorization of 96 are 2 × 2 × 2 × 2 × 2 × 3
Graph the inequality in a coordinate plane.
Question 53.
y ≤ 4x – 1
Answer:
Question 54.
y > – \(\frac{1}{2}\)x + 3
Answer:
Question 55.
4y – 12 ≥ 8x
Answer:
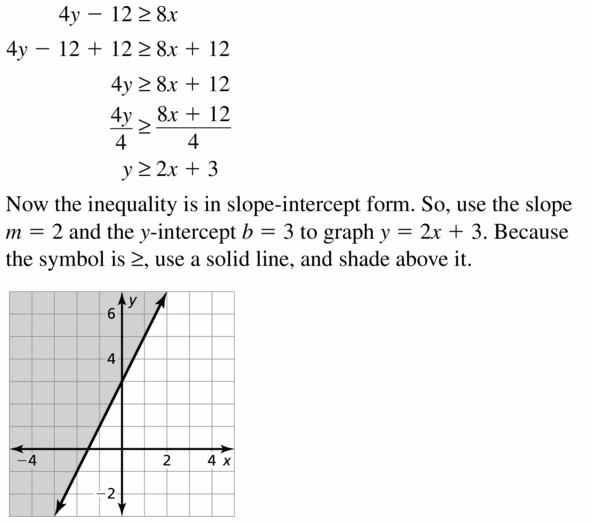
Question 56.
3y + 3 < x
Answer:
Lesson 7.8 Factoring Polynomials Completely
Essential Question How can you factor a polynomial completely?
EXPLORATION 1
Writing a Product of Linear Factors
Work with a partner. Write the product represented by the algebra tiles. Then multiply to write the polynomial in standard form.
Answer:
a. (x + 1)(x + 1)(-2) = (x + 1)² – 2 = x² + 2x + 1 – 2 = x² + 2x – 1
b. (x + 2)(x + 1)(-x) = (x + 2)(-x² – x) = -x³ – 2x² – x² – 2x = -x² – 3x² – 2x
c. (x + 3)(x)(2) = (x² + 3x)2 = 2x² + 6x
d. (x + 1)(x – 1)(x) = (x² – 1)x = x³ – x
e. (-x + 1)(x + 1)(-x) = (1 – x²)(-x) = -x + x³
f. (-x – 1)(x + 1)(-2) = (-x² – 1)(-2) = 2x² + 2
EXPLORATION 2
Matching Standard and Factored Forms

Work with a partner. Match the standard form of the polynomial with the equivalent factored form. Explain your strategy.

Answer:
a. x³ + x² = x²(x + 1) – J
b. x³ – x = x(x² – 1) = x(x + 1)(x – 1) – A
c. x³ + x² – 2x = x(x² + x – 2) = x(x² + 2x – 1x – 2) = x(x(x + 2) – 1(x + 2)) = x(x – 1)(x + 2) – D
d. x³ – 4x² + 4x = x(x² – 4x + 4) = x(x – 2)² – G
e. x³ – 2x² – 3x = x(x² – 2x – 3) = x(x² – 3x + 1x – 3) = x(x(x – 3) + 1(x – 3)) = x(x – 3)(x + 1) – N
f. x³ – 2x² + x = x(x² – 2x + 1) = x(x – 1)² – B
g. x³ – 4x = x(x² – 4) = x(x + 2)(x – 2) – F
h. x³ + 2x² = x²(x + 2) – L
i. x³ – x² = x²(x – 1) – I
j. x³ – 3x² + 2x = x(x² – 3x + 2) = x(x² – 2x – 1x + 2) = x(x(x – 2) – 1(x – 2)) = x(x – 2)(x – 1) – E
k. x³ + 2x² – 3x = x(x² + 2x – 3) = x(x² + 3x – 1x – 3) = x(x(x + 3) – 1(x + 3)) = x(x + 3)(x – 1) – M
i. x³ – 4x² + 3x = x(x² – 4x + 3) = x(x² – 3x – 1x + 3) = x(x(x – 3) – 1(x – 3)) = x(x – 3)(x – 1) – O
m. x³ – 2x² = x²(x – 2) – K
n. x³ + 4x² + 4x = x(x² + 4x + 4) = x(x + 2)² – H
o. x³ + 2x² + x = x(x² + 2x + 1) = x(x + 1)² – C
Communicate Your Answer
Question 3.
How can you factor a polynomial completely?
Answer:
1. Group the first two terms together and then the last terms together.
2. Factor out a GCF from each separate binomial.
3. Factor out the common binomial.
Question 4.
Use your answer to Question 3 to factor each polynomial completely.
a. x3 + 4x2 + 3x
b. x3 – 6x2 + 9x
c. x3 + 6x2 + 9x
Answer:
a. x3 + 4x2 + 3x = x(x² + 4x + 3) = x(x² + 3x + 1x + 3) = x(x(x + 3) + 1(x + 3)) = x(x + 1)(x + 3)
b. x3 – 6x2 + 9x = x(x² – 6x + 9) = x(x – 3)²
c. x3 + 6x2 + 9x= x(x² + 6x + 9) = x(x + 3)²
Factor the polynomial by grouping.
Question 1.
a3 + 3a2 + a + 3
Answer:
Given,
a3 + 3a2 + a + 3
= a³ + 3a² + (a + 3)
= a²(a + 3) + 1(a + 3)
= (a² + 1)(a + 3)
Question 2.
y2 + 2x + yx + 2y
Answer:
Given,
y² + 2x + xy + 2y
= y(y + x) + 2(x + y)
= (y + 2)(x + y)
Factor the polynomial completely.
Question 3.
3x3 – 12x
Answer:
3x³ – 12x
3x(x² – 4)
Question 4.
2y3 – 12y2 + 18y
Answer:
2y³ – 12y² + 18y
= 2y(y² – 6y + 9)
= 2y(y – 3)²
Question 5.
m3 – 2m2 – 8m
Answer:
m³ – 2m² – 8m
= m(m² – 2m – 8)
= m(m² – 4m + 2m – 8)
= m(m(m – 4) + 2(m – 4))
= m(m – 4)(m + 2)
Solve the equation.
Question 6.
w3 – 8w2 + 16w = 0
Answer:
w³ – 8w² + 16w = 0
w(w² – 8w + 16) = 0
w² – 8w + 16 = 0
w² – 4w – 4w + 16 = 0
w(w – 4) -4 (w – 4) = 0
(w – 4)(w – 4) = 0
w = 4, 4
Question 7.
x3 – 25x = 0
Answer:
x³ – 25x = 0
x(x² – 25) = 0
x² – 25 = 0
x² – 5² = 0
x² = 5²
x = 5
Question 8.
c3 – 7c2 + 12c = 0
Answer:
c³ – 7c² + 12c = 0
c² – 7c + 12 = 0
c² – 3c – 4c + 12 = 0
c(c – 3) – 4(c – 3) = 0
(c – 3)(c – 4) = 0
c = 3, 4
Question 9.
A box in the shape of a rectangular prism has a volume of 72 cubic feet. The box has a length of x feet, a width of (x – 1) feet, and a height of (x + 9) feet. Find the dimensions of the box.
Answer:
Given,
A box in the shape of a rectangular prism has a volume of 72 cubic feet.
The box has a length of x feet, a width of (x – 1) feet, and a height of (x + 9) feet.
x(x – 1)(x + 9) = 72
(x² – x)(x + 9) = 72
x³ + 9x² – x² – 9x = 72
x³ + 8x² – 9x = 72
x³ + 8x² – 9x – 72 = 0
x²(x + 8) – 9(x + 8) = 0
(x + 8)(x² – 9) = 0
x = -8, x = 3
Dimensions cannot be negative.
So, x = 3
w = x – 1 = 3 – 1 = 2 feet
height = x + 9 = 3 + 9 = 12 feet
Factoring Polynomials Completely 7.8 Exercises
Vocabulary and Core Concept Check
Question 1.
VOCABULARY
What does it mean for a polynomial to be factored completely?
Answer:

Question 2.
WRITING
Explain how to choose which terms to group together when factoring by grouping.
Answer:

Monitoring Progress and Modeling with Mathematics
In Exercises 3–10, factor the polynomial by grouping.
Question 3.
x3 + x2 + 2x + 2
Answer:
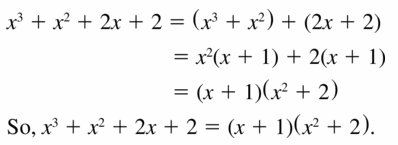
Question 4.
y3 – 9y2+ y – 9
Answer:

Question 5.
3z3 + 2z – 12z2 – 8
Answer:
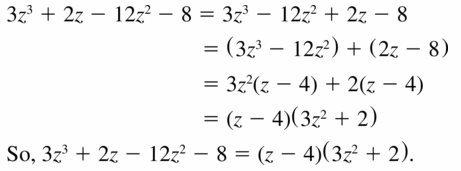
Question 6.
2s3 – 27 – 18s + 3s2
Answer:

Question 7.
x2 + xy + 8x + 8y
Answer:
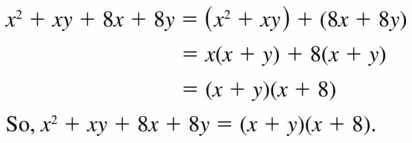
Question 8.
q2 + q + 5pq + 5p
Answer:

Question 9.
m2 – 3m + mn – 3n
Answer:
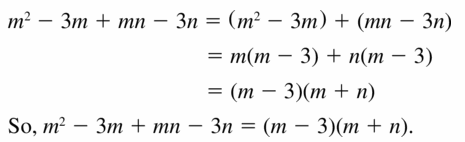
Question 10.
2a2 + 8ab – 3a – 12b
Answer:

In Exercises 11–22, factor the polynomial completely.
Question 11.
2x3 – 2x
Answer:
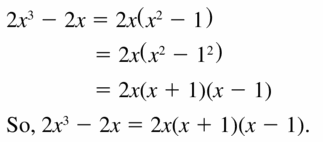
Question 12.
36a4 – 4a2
Answer:

Question 13.
2c2 – 7c + 19
Answer:
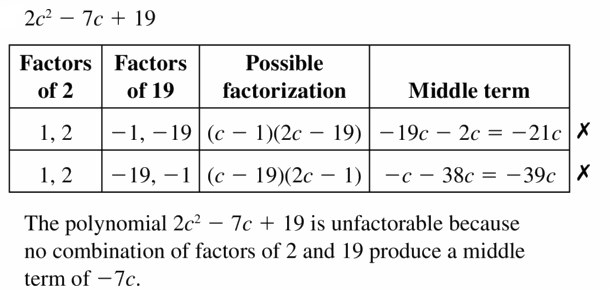
Question 14.
m2 – 5m – 35
Answer:

Question 15.
6g3 – 24g2 + 24g
Answer:
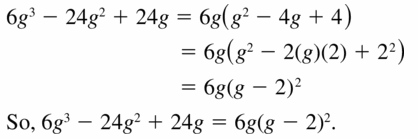
Question 16.
-15d3 + 21d2 – 6d
Answer:

Question 17.
3r5 + 3r4 – 90r3
Answer:
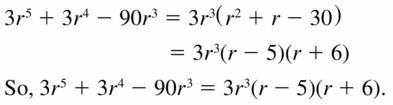
Question 18.
5w4 – 40w3 + 80w2
Answer:

Question 19.
-4c4 + 8c3 – 28c2
Answer:
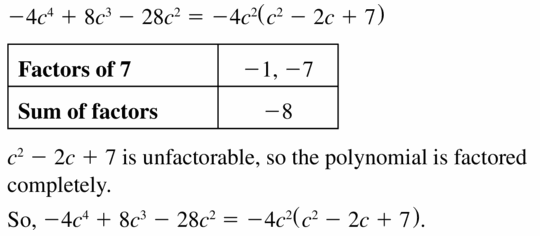
Question 20.
8t2 + 8t – 72
Answer:

Question 21.
b3 – 5b2 – 4b + 20
Answer:
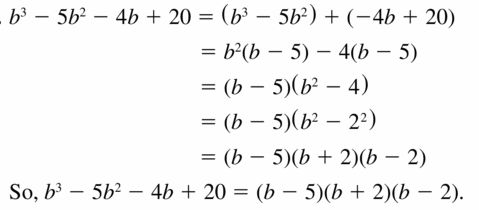
Question 22.
h3 + 4h2 – 25h – 100
Answer:

In Exercises 23–28, solve the equation.
Question 23.
5n3 – 30n2 + 40n = 0
Answer:
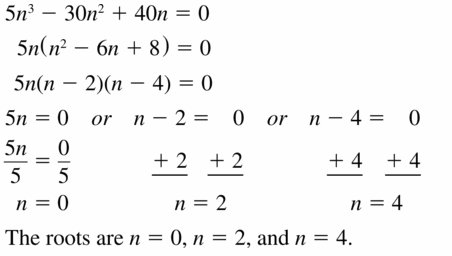
Question 24.
k4 – 100k2 = 0
Answer:

Question 25.
x3 + x2 = 4x + 4
Answer:
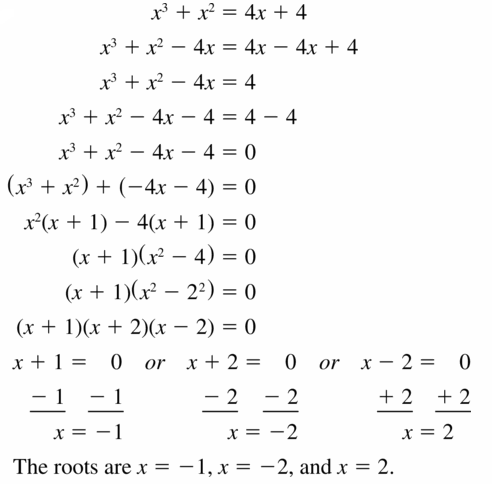
Question 26.
2t5 + 2t4 – 144t3 = 0
Answer:
2t5 + 2t4 – 144t3 = 0
2t³(t² + t – 72) = 0
t² + t – 72 = 0
t² + 9t – 8t – 72 = 0
t(t + 9) – 8(t + 9) = 0
(t + 9)(t – 8) = 0
t = 8, -9
Question 27.
12s – 3s3 = 0
Answer:
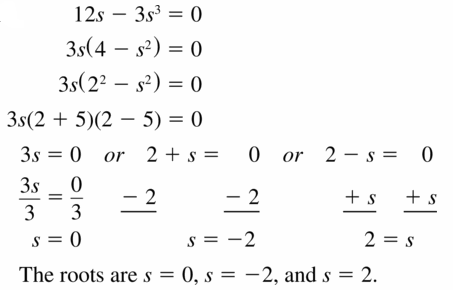
Question 28.
4y3 – 7y2 + 28 = 16y
Answer:
4y³ – 7y² + 28 = 16y
4y³ – 7y² – 16y + 28 = 0
y²(4y – 7) – 4(4y – 7) = 0
(4y – 7)(y² – 4) = 0
4y – 7 = 0 or y² – 4 = 0
y = 7/4 or y² = 4
y = 7/4 or 2
In Exercises 29–32, find the x-coordinates of the points where the graph crosses the x-axis.
Question 29.
Answer:
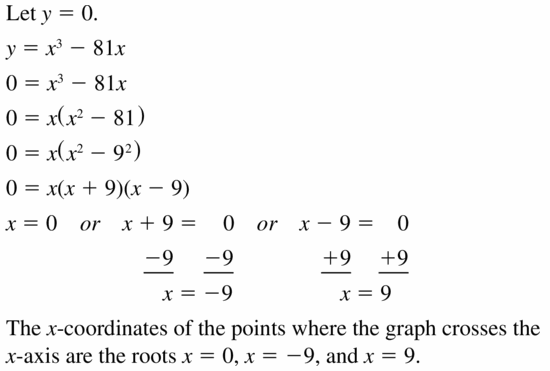
Question 30.
Answer:
y = -3x4 – 24x³ – 45x²
y = 0
-3x4 – 24x³ – 45x² = 0
x²(-3x² – 24x – 45) = 0
-3x² – 24x – 45 = 0
x² + 8x + 15 = 0
x² + 3x + 5x + 15 = 0
x(x + 3) + 5(x + 3) = 0
(x + 3)(x + 5) = 0
x = -3, -5
Question 31.
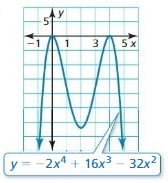
Answer:
Question 32.
Answer:
y = 4x³ + 25x² – 56x
4x³ + 25x² – 56x = 0
x(4x² + 25x – 56) = 0
4x² + 25x – 56 = 0
4x² + 32x – 7x – 56 = 0
4x(x + 8) – 7(x + 8) = 0
(x + 8)(4x – 7) = 0
x = -8, 7/4
ERROR ANALYSIS In Exercises 33 and 34, describe and correct the error in factoring the polynomial completely.
Question 33.
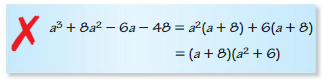
Answer:
Question 34.
Answer:
x³ – 6x² – 9x + 54
= x²(x – 6) – 9(x – 6)
= (x – 6)(x² – 9)
Question 35.
MODELING WITH MATHEMATICS
You are building a birdhouse in the shape of a rectangular prism that has a volume of 128 cubic inches. The dimensions of the birdhouse in terms of its width are shown.
a. Write a polynomial that represents the volume of the birdhouse.
b. What are the dimensions of the birdhouse?
Answer:


Question 36.
MODELING WITH MATHEMATICS
A gift bag shaped like a rectangular prism has a volume of 1152 cubic inches. The dimensions of the gift bag in terms of its width are shown. The height is greater than the width. What are the dimensions of the gift bag?
Answer:
Given,
l = 2w + 4
h = 18 – w
w = w
V = lwh
V = 1152
1152 = (2w + 4)(w)(18 – w)
-2w³ + 36w² – 4w² + 72w = 1152
-2w³ + 32w² + 72w = 1152
-w³ + 16w² – 36w + 576 = 0
-w²(w – 16) -36(w – 16) = 0
(w – 16)(-w² – 36) = 0
w = 16 or w = -6
w = 16
w = 6 in
l = 16 in
h = 12 in.
In Exercises 37–40, factor the polynomial completely.
Question 37.
x3 + 2x2y – x – 2y
Answer:
Question 38.
8b3 – 4b2a – 18b + 9a
Answer:
Question 39.
4s2 – s + 12st – 3t
Answer:
Question 40.
6m3 – 12mn + m2n – 2n2
Answer:
Question 41.
WRITING
Is it possible to find three real solutions of the equation x3 + 2x2 + 3x + 6 = 0? Explain your reasoning.
Answer:

Question 42.
HOW DO YOU SEE IT?
How can you use the factored form of the polynomial x4 – 2x3 – 9x2 + 18x = x(x – 3)(x + 3)(x – 2) to find the x-intercepts of the graph of the function?
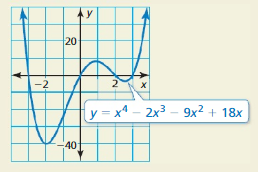
Answer:
Question 43.
OPEN-ENDED
Write a polynomial of degree 3 that satisfies each of the given conditions.
a. is not factorable
b. can be factored by grouping
Answer:
Question 44.
MAKING AN ARGUMENT
Your friend says that if a trinomial cannot be factored as the product of two binomials, then the trinomial is factored completely. Is your friend correct? Explain.
Answer:
If a trinomial cannot be factored as the product of two binomials, then the trinomial is factored completely.
In fact, a trinomial ax² + bx + c can be factored only if it can be written as the product of two binomials say (ax + n)(x + m)
c = mn
ac = pq
b = p + q
= am + n
Hence, the given statement trinomial cannot be factored as the product of two binomials, then the trinomial cannot be factored completely.
Question 45.
PROBLEM SOLVING
The volume (in cubic feet) of a room in the shape of a rectangular prism is represented by 12z3 – 27z. Find expressions that could represent the dimensions of the room.
Answer:
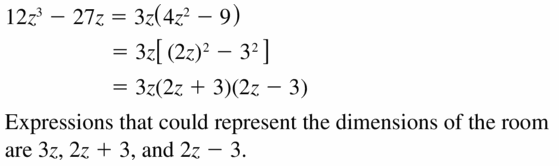
Question 46.
MATHEMATICAL CONNECTIONS
The width of a box in the shape of a rectangular prism is 4 inches more than the height h. The length is the difference of 9 inches and the height.
a. Write a polynomial that represents the volume of the box in terms of its height (in inches).
b. The volume of the box is 180 cubic inches. What are the possible dimensions of the box?
c. Which dimensions result in a box with the least possible surface area? Explain your reasoning.
Answer:
Given,
The width of a box in the shape of a rectangular prism is 4 inches more than the height h.
The length is the difference of 9 inches and the height.
V = lwh
V = h(h + 4)(9 – h)
V = h(5h – h² + 36)
= -h³ + 5h² + 36h
V = 180 cu. in
180 = -h³ + 5h² + 36h
h = 5 or 6
The volume of the box is -h³ + 5h² + 36h.
Question 47.
MATHEMATICAL CONNECTIONS
The volume of a cylinder is given by V = πr2h, where r is the radius of the base of the cylinder and h is the height of the cylinder. Find the dimensions of the cylinder.
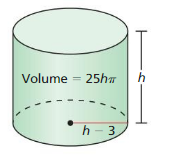
Answer:
Question 48.
THOUGHT PROVOKING
Factor the polynomial x5 – x4 – 5x3 + 5x2 + 4x – 4 completely.
Answer:
x5 – x4 – 5x3 + 5x2 + 4x – 4
x4(x – 1) – 5x²(x – 1) + 4(x – 1)
(x – 1)(x4 – 5x² + 4)
Question 49.
REASONING
Find a value for w so that the equation has (a) two solutions and (b) three solutions. Explain your reasoning. 5x3 + wx2 + 80x = 0
Answer:

Maintaining Mathematical Proficiency
Solve the system of linear equations by graphing.
Question 50.
y = x – 4
y = -2x + 2
Answer:

Question 51.
y = \(\frac{1}{2}\)x + 2
y = 3x – 3
Answer:
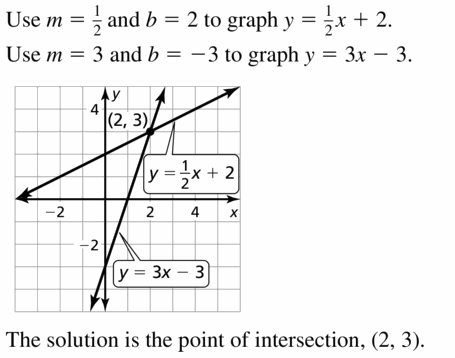
Question 52.
5x – y = 12
\(\frac{1}{4}\)x + y = 9
Answer:
Question 53.
x = 3y
y – 10 = 2x
Answer:
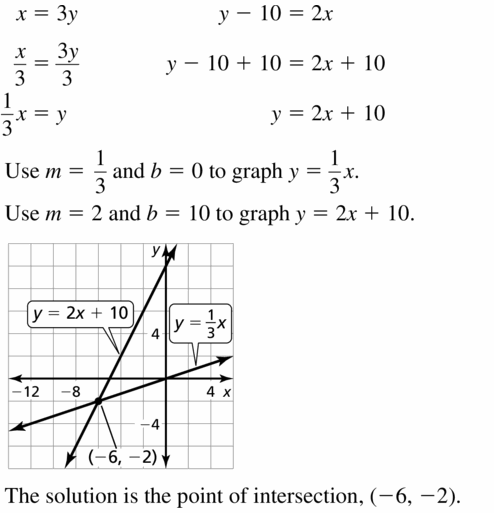
Graph the function. Describe the domain and range.
Question 54.
f(x) = 5x
Answer:
Question 55.
y = 9 (\(\frac{1}{3}\))x
Answer:
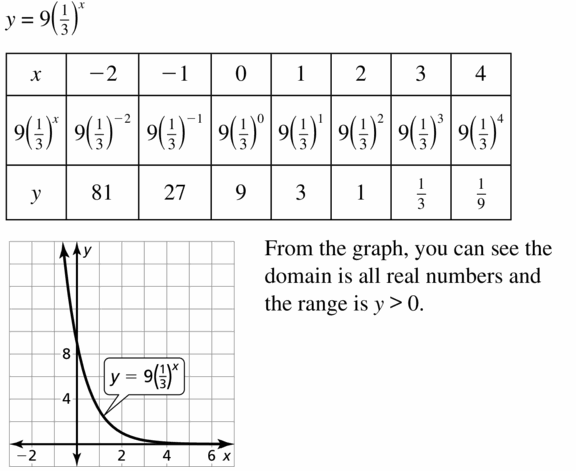
Question 56.
y = -3(0.5)x
Answer:
Question 57.
f(x) = -3(4)x
Answer:

Polynomial Equations and Factoring Performance Task: The View Matters
7.5 – 7.8 What Did You Learn?
Core Vocabulary
factoring by grouping, p. 404
factored completely, p. 404
Core Concepts
Section 7.5
Factoring x2 + bx + c When c Is Positive, p. 386
Factoring x2 + bx + c When cIs Negative, p. 387
Section 7.6
Factoring ax2 + bx + c When ac Is Positive, p. 392
Factoring ax2 + bx + c When ac Is Negative, p. 393
Section 7.7
Difference of Two Squares Pattern, p. 398
Perfect SquareTrinomial Pattern, p. 399
Section 7.8
Factoring by Grouping, p. 404
Factoring Polynomials Completely, p. 404
Mathematical Practices
Question 1.
How are the solutions of Exercise 29 on page 389 related to the graph of y = m2 + 3m + 2?
Answer:
Question 2.
The equation in part (b) of Exercise 47 on page 390 has two solutions. Are both solutions of the equation reasonable in the context of the problem? Explain your reasoning.
Answer:
Performance Task: The View Matters
The way an equation or expression is written can help you interpret and solve problems. Which representation would you rather have when trying to solve for specific information? Why?
To explore the answers to these questions and more, go to

Polynomial Equations and Factoring Chapter Review
7.1 Adding and Subtracting Polynomials
Write the polynomial in standard form. Identify the degree and leading coefficient of the polynomial. Then classify the polynomial by the number of terms.
Question 1.
6 + 2x2
Answer:
6 + 2x2
We have to write the polynomial in standard form
2x² + 6
The degree of the polynomial is 2
coefficient is 2
There are 2 terms in the polynomial so it is binomial.
Question 2.
-3p3 + 5p6 – 4
Answer:
-3p3 + 5p6 – 4
We have to write the polynomial in standard form
5p6 -3p3 – 4
The degree of the polynomial is 6
the coefficient is 5, -3
There are 3 terms in the polynomial so it is a trinomial.
Question 3.
9x7 – 6x2 + 13x5
Answer:
9x7 – 6x2 + 13x5
We have to write the polynomial in standard form
9x7 + 13x5 – 6x2
The degree of the polynomial is 7
the coefficient is 9, 13 and -6
There are 3 terms in the polynomial so it is a trinomial.
Question 4.
-12y + 8y3
Answer:
-12y + 8y3
We have to write the polynomial in standard form
8y3 -12y
The degree of the polynomial is 3
the coefficient is 8, -12
There are 2 terms in the polynomial so it is binomial.
Find the sum or difference.
Question 5.
(3a + 7) + (a – 1)
Answer:
(3a + 7) + (a – 1)
3a + 7 + a – 1
Combine the like terms
3a + a + 7 – 1
4a + 6
(3a + 7) + (a – 1) = 4a + 6
Question 6.
(x2 + 6x – 5) + (2x2 + 15)
Answer:
(x2 + 6x – 5) + (2x2 + 15)
x2 + 6x – 5 + 2x2 + 15
3x² + 6x + 10
(x2 + 6x – 5) + (2x2 + 15) = 3x² + 6x + 10
Question 7.
(-y2 + y + 2) – (y2 – 5y – 2)
Answer:
(-y2 + y + 2) – (y2 – 5y – 2)
-y2 + y + 2 – y2 + 5y + 2
-2y² + 6y + 4
(-y2 + y + 2) – (y2 – 5y – 2) = -2y² + 6y + 4
Question 8.
(p + 7) – (6p2 + 13p)
Answer:
(p + 7) – (6p2 + 13p)
p + 7 – 6p2 + 13p
-6p² + 14p + 7
7.2 Multiplying Polynomials
Find the product.
Question 9.
(x + 6)(x – 4)
Answer:
(x + 6)(x – 4)
= x(x – 4) + 6(x – 4)
= x² – 4x + 6x – 24
= x² + 2x – 24
Question 10.
(y – 5)(3y + 8)
Answer:
(y – 5)(3y + 8)
= y(3y + 8) – 5(3y + 8)
= 3y² + 8y – 15y – 40
= 3y² – 7y – 40
Question 11.
(x + 4)(x2 + 7x)
Answer:
(x + 4)(x2 + 7x)
= x(x2 + 7x) + 4(x2 + 7x)
= x³ + 7x² + 4x² + 28x
= x³ + 11x² + 28x
Question 12.
(-3y + 1)(4y2 – y – 7)
Answer:
(-3y + 1)(4y2 – y – 7)
= -3y(4y2 – y – 7) + 1(4y2 – y – 7)
= 12y³ + 3y² + 21y + 4y² – y – 7
= 12y³ + 7y² + 20y – 7
7.3 Special Products of Polynomials
Find the product.
Question 13.
(x + 9)(x – 9)
Answer:
Given,
(x + 9)(x – 9)
It is in the form of (a + b)(a – b) = a² – b²
(x + 9)(x – 9) = (x)² – (9)²
= x² – 81
Question 14.
(2y + 4)(2y – 4)
Answer:
It is in the form of (a + b)(a – b) = a² – b²
(2y + 4)(2y – 4) = (2x)² – (4)²
= 4x² – 16
Question 15.
( p + 4)2
Answer:
(p + 4)2
It is in the form of (a + b)² = a² + b² + 2ab
(p + 4)² = p² + 4² + 2.p.4
= p² + 16 + 8p
= p² + 8p + 16
Question 16.
(-1+ 2d )2
Answer:
(-1+ 2d)² = (2d – 1)²
It is in the form of (a – b)² = a² + b² – 2ab
(2d – 1)² = (2d)² + 1² – 2(2d)(1)
= 4d² + 1 – 4d
7.4 Solving Polynomial Equations in Factored Form (pp. 377–382)
Solve the equation.
Question 17.
x2 + 5x = 0
Answer:
Given,
x2 + 5x = 0
x(x + 5) = 0
x = 0 or x+ 5 = 0
x = 0 or x = -5
So, x = 0, -5
Question 18.
(z + 3)(z – 7) = 0
Answer:
Given,
(z + 3)(z – 7) = 0
z + 3 = 0 or z – 7 = 0
z = -3 or z = 7
So, z = -3, 7
Question 19.
(b + 13)2 = 0
Answer:
Given,
(b + 13)2 = 0
b + 13 = 0
b = -13
Question 20.
2y(y – 9)(y + 4) = 0
Answer:
Given,
2y(y – 9)(y + 4) = 0
2y = 0 or y – 9 = 0 or y + 4 = 0
y = 0 or y = 9 or y = -4
So, y = 0, 9, -4
7.5 Factoring x2 + bx + c(pp. 385–390)
Factor the polynomial.
Question 21.
p2 + 2p – 35
Answer:
p2 + 2p – 35
7 × 5 = 35
p² + 7p – 5p – 35
p(p + 7) – 5(p + 7)
(p – 5)(p + 7)
p – 5 = 0 or p + 7 = 0
p = 5 or p = -7
Question 22.
b2 + 18b + 80
Answer:
b2 + 18b + 80
b² + 10b + 8b + 80
b(b + 10) + 8(b + 10)
(b + 10)(b + 8)
b + 10 = 0 or b + 8 = 0
b = -10, -8
Question 23.
z2 – 4z – 21
Answer:
z2 – 4z – 21
z² – 7z + 3z – 21
z(z – 7) + 3(z – 7)
(z – 7)(z + 3)
z = 7, -3
Question 24.
x2 – 11x + 28
Answer:
x2 – 11x + 28
x² – 7x – 4x + 28
x(x – 7) – 4(x – 7)
(x – 4)(x – 7)
x = 4, 7
7.6 Factoring ax2 + bx + c (pp. 391–396)
Factor the polynomial.
Question 25.
3t2 + 16t – 12
Answer:
3t2 + 16t – 12
3t² + 18t – 2t – 12
3t(t + 6) – 2(t + 6)
(t + 6)(3t – 2)
t = 6 or t = 2/3
So, t = 6, 2/3
Question 26.
-5y2 – 22y – 8
Answer:
-5y2 – 22y – 8
-5y² – 20y – 2y – 8
-5y(y + 4) – 2(y + 4)
(y + 4)(-5y – 2)
y + 4 = 0 or -5y – 2 = 0
y = -4 or y = -2/5
so, y = 4, -2/5
Question 27.
6x2 + 17x + 7
Answer:
6x2 + 17x + 7
7 × 6 = 42
6x² + 3x + 14x + 7
3x(2x + 1) + 7(2x + 1)
(3x + 7)(2x + 1)
x = -7/3, -1/2
Question 28.
-2y2 + 7y – 6
Answer:
-2y2 + 7y – 6
-2y² + 3y + 4y – 6
-y(2y – 3) + 2(2y – 3)
(2y – 3)(-y + 2)
y = 3/2, -2
Question 29.
3z2 + 26z – 9
Answer:
3z2 + 26z – 9
3z2 + 27 z -1z – 9
3z(z + 9) -1(z + 9)
(3z – 1)(z + 9)
z = -9, 1/3
Question 30.
10a2 – 13a – 3
Answer:
10a2 – 13a – 3
10a2 – 15a + 2a – 3
5a(2a – 3) + 1(2a – 3)
(2a – 3)(5a + 1)
2a – 3 = 0 or 5a + 1 = 0
2a = 3 or 5a = -1
a = 3/2, -1/5
7.7 Factoring Special Products (pp. 397–402)
Factor the polynomial.
Question 31.
x2 – 9
Answer:
x2 – 9
It is in the form of a² – b² = (a + b)(a – b)
x2 – 9 = x2 – 3² = (x + 3)(x – 3)
Question 32.
y2 – 100
Answer:
y2 – 100
It is in the form of a² – b² = (a + b)(a – b)
y2 – 100 = y2 – 10² = (y + 10)(y – 10)
Question 33.
z2 – 6z + 9
Answer:
z2 – 6z + 9
It is in the form of (a – b)² = a² + b² – 2ab
z2 – 6z + 9 = (z – 3)²
Question 34.
m2 + 16m + 64
Answer:
m2 + 16m + 64
It is in the form of (a + b)² = a² + b² + 2ab
m2 + 16m + 64 = (m + 8)²
7.8 Factoring Polynomials Completely (pp. 403–408)
Factor the polynomial completely.
Question 35.
n3 – 9n
Answer:
Given polynomial
n3 – 9n
n(n² – 9)
n = 0 or n² – 9 = 0
n = 0 or n² = 9
n = 0, 3
Question 36.
x2 – 3x + 4ax – 12a
Answer:
Given polynomial
x2 – 3x + 4ax – 12a
x(x – 3) + 4a(x – 3)
(x – 3)(x + 4a) = 0
x – 3 = 0 or x + 4a = 0
x = 3 or a = -4a
Question 37.
2x4 + 2x3 – 20x2
Answer:
Given polynomial
2x4 + 2x3 – 20x2
2x²(x² + x – 10)
2x² = 0 or x² + x – 10 = 0
Solve the equation.
Question 38.
3x3 – 9x2 – 54x = 0
Answer:
Given polynomial
3x3 – 9x2 – 54x = 0
3x(x² – 3x – 18) = 0
x² – 3x – 18 = 0
x² – 6x + 3x – 18 = 0
x(x – 6) + 3(x – 6) = 0
(x + 3)(x – 6) = 0
x = -3, 6
Question 39.
16x2 – 36 = 0
Answer:
Given polynomial
16x2 – 36 = 0
4(4x² – 9) = 0
4x² – 9 = 0
4x² = 9
x² = 9/4
x = 3/2
Question 40.
z3 + 3z2 – 25z – 75 = 0
Answer:
Given polynomial
z3 + 3z2 – 25z – 75 = 0
z²(z + 3) – 25(z + 3) = 0
(z + 3)(z² – 25) = 0
z = -3 or z² = 25
z = -3, 5
Question 41.
A box in the shape of a rectangular prism has a volume of 96 cubic feet. The box has a length of (x + 8) feet, a width of x feet, and a height of (x – 2) feet. Find the dimensions of the box.
Answer:
l = x + 8
w = x
h = x – 2
V = lbh
96 = (x + 8)(x)(x – 2)
(x + 8)(x² – 2x) = 96
x³ – 2x² + 8x² – 16x = 96
x³ + 6x² – 16x – 96 = 0
(x + 6)(x + 4)(x – 4)
x = -6, -4, 4
x =-6 ⇒ -6 + 8 = 2
length = x + 8
w = x ⇒ -6
h = x – 2 ⇒ -6 – 2 = -8
x =-4 ⇒ -4 + 8 = 4
length = x + 8
w = x ⇒ -4
h = x – 2 ⇒ -4 – 2 = -6
x =4 ⇒ 4 + 8 = 12
length = x + 8
w = x ⇒ 4
h = x – 2 ⇒ 4 – 2 = 2
Polynomial Equations and Factoring Chapter Test
Find the sum or difference. Then identify the degree of the sum or difference and classify it by the number of terms.
Question 1.
(-2p + 4) – (p2 – 6p + 8)
Answer:
Given polynomial (-2p + 4) – (p2 – 6p + 8)
= -2p + 4 – p2 + 6p – 8
= -p² – 2p + 6p + 4 – 8
= -p² + 4p – 4
Question 2.
(9c6 – 5b4) – (4c6 – 5b4)
Answer:
Given polynomial (9c6 – 5b4) – (4c6 – 5b4)
= 9c6 – 5b4 – 4c6 + 5b4
= 9c6 – 4c6 + 5b4 – 5b4
= 5c6
Question 3.
(4s4 + 2st + t) + (2s4 – 2st – 4t)
Answer:
(4s4 + 2st + t) + (2s4 – 2st – 4t)
= 4s4 + 2st + t + 2s4 – 2st – 4t
= 6s4 + 2st – 2st + t – 4t
= 6s4 – 3t
Find the product.
Question 4.
(h – 5)(h – 8)
Answer:
Given,
(h – 5)(h – 8)
= h(h – 8) – 5(h – 8)
= h² – 8h – 5h + 40
= h² -13h + 40
So, the product of (h – 5)(h – 8) is h² -13h + 40
Question 5.
(2w – 3)(3w + 5)
Answer:
(2w – 3)(3w + 5)
= 2w(3w + 5) – 3(3w + 5)
= 6w² + 10w – 9w – 15
Question 6.
(z + 11)(z – 11)
Answer:
(z + 11)(z – 11)
= z(z – 11) + 11(z – 11)
= z² – 11z + 11z – 121
= z² – 121
Question 7.
Explain how you can determine whether a polynomial is a perfect square trinomial.
Answer:
A polynomial is a perfect square trinomial if the first and last terms are perfect squares, and the middle term’s coefficient is twice the product of the square roots of the first and last terms.
Question 8.
Is 18 a polynomial? Explain your reasoning.
Answer:
Polynomial is an expression involving variables and constants such that variables have non-negative integer power.
Example:
2z4, 3y³
So, yes 18 is a polynomial.
18x0 = 1
Factor the polynomial completely.
Question 9.
s2 – 15s + 50
Answer:
s² – 15s + 50
= s² – 5s – 10s + 50
= s(s – 5) – 10(s – 5)
= (s – 5)(s – 10)
s – 5 = 0 or s – 10 = 0
s = 5 or s = 10
Question 10.
h3 + 2h2 – 9h – 18
Answer:
h3 + 2h2 – 9h – 18
= h²(h + 2) -2h(h + 2)
= (h² – 2h)(h + 2)
h² – 2h = 0 or h + 2 = 0
h² = 2h or h = -2
h = 2 or h = -2
Question 11.
-5k2 – 22k + 15
Answer:
-5k2 – 22k + 15
15 × 5 = 75
Factors of 75 are 1, 3, 5, 15, 25 and 75
-5k² – 25k + 3k + 15
-5k(k + 5) + 3(k + 5)
(-5k + 3)(k + 5)
Solve the equation.
Question 12.
(n – 1)(n + 6)(n + 5) = 0
Answer:
Given equation (n – 1)(n + 6)(n + 5) = 0
n – 1 = 0 or n + 6 = 0 or n + 5 = 0
n = 1 or n = -6 or n = -5
Question 13.
d2 + 14d + 49 = 0
Answer:
d2 + 14d + 49 = 0
d² + 7d + 7d + 49 = 0
d(d + 7) + 7(d + 7) = 0
(d + 7)(d + 7) = 0
d = -7
Question 14.
6x4 + 8x2 = 26x3
Answer:
x²(6x² + 8) = (26x)x²
6x² + 8 = 26x
6x² + 8 – 26x = 0
3x² + 4 – 13x = 0
3x² – 13x + 4 = 0
3x² – 12x – 1x + 4 = 0
3x(x – 4) -1(x – 4) = 0
(x – 4)(3x – 1) = 0
x – 4 = 0 or 3x – 1 = 0
x = 4 or 3x = 1
x = 1/3 or 4
Question 15.
The expression π(r – 3)2 represents the area covered by the hour hand on a clock in one rotation, where r is the radius of the entire clock. Write a polynomial in standard form that represents the area covered by the hour hand in one rotation.
Answer:
(r – 3)2 can be written as (r – 3)(r – 3).
r(r – 3) – 3(r – 3)
r² – 3r – 3r + 9
r² – 6r + 9
π(r² – 6r + 9)
Distribute pi to each term to get a final of π(r²) – π(6r) + π(9)
Question 16.
A magician’s stage has a trapdoor.
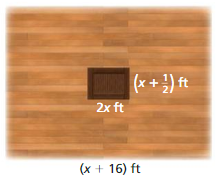
a. The total area (in square feet) of the stage can be represented by x2 + 27x + 176. Write an expression for the width of the stage.
Answer:
x2 + 27x + 176
x² + 16 + 11x + 176
x(x + 16) + 11(x +16)
(x + 16)(x + 11)
As the length is (x + 16) the width is area/length
So, the width is x + 11.
b. Write an expression for the perimeter of the stage.
Answer:
The total area (in square feet) of the stage can be represented by x2 + 27x + 176.
2(x + 16 + x + 11) or 2(2x + 27)
So, the perimeter of the stage is 2(x + 16 + x + 11) or 2(2x + 27).
c. The area of the trapdoor is 10 square feet. Find the value of x.
Answer:
Given,
The area of the trapdoor is 10 square feet.
Area = 2x(x + 1/2)
2x(x + 1/2) = 10
2x² + x – 10 = 0
2x² + 5x – 4x – 10 = 0
x(2x + 5) -2(2x + 5) = 0
(2x + 5)(x – 2)
2x + 5 = 0 or x – 2 = 0
x = -5/2 or x = 2
d. The magician wishes to have the area of the stage be at least 20 times the area of the trapdoor. Does this stage satisfy his requirement? Explain.
Answer:
Given,
The magician wishes to have the area of the stage be at least 20 times the area of the trapdoor.
x2 + 27x + 176 = 20(2x² + x – 10)
The expression for area of stage becomes x2 + 27x + 176 = 40x² + 20x – 200
39x² – 17x – 376 = 0
√(b² – 4ac = √(-17)² -4(39)(-376)
The discriminant is a positive value.
So, the equation will have real roots stating that the stage satisfies his requirements.
Question 17.
Write a polynomial equation in factored form that has three positive roots.
Answer:
When a polynomial is in factored form, then it is of the form
f(x) = a(x – h)(x – k)(x – r)
where a, h, k and r are constants
Example:
f(x) = 2(x – 1)(x – 2)(x – 2)
Question 18.
You are jumping on a trampoline. For one jump, your height y (in feet) above the trampoline after t seconds can be represented by y = -16t2 + 24t. How many seconds are you in the air?
Answer:
Given y = -16t2 + 24t
-8t(2t – 3) = 0
-8t = 0 or 2t – 3 = 0
t = 0 or t = 3/2
So, t = 0, 3/2
Question 19.
A cardboard box in the shape of a rectangular prism has the dimensions shown.
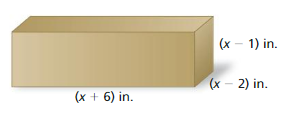
a. Write a polynomial that represents the volume of the box.
b. The volume of the box is 60 cubic inches. What are the length, width, and height of the box?
Answer:
Given,
l = (x + 6) inch
b = (x – 2) inch
h = (x – 1) inch
A = lbh
= (x + 6)(x – 2)(x – 1)
= (x + 6)(x(x – 1)-2(x – 1))
= (x + 6)(x² – x – 2x + 2)
= (x + 6)(x² – 3x + 2)
= x(x² – 3x + 2) + 6(x² – 3x + 2)
= x³ – 3x² + 2x + 6x² – 18x + 12
= x³ + 3x² – 16x + 12
Polynomial Equations and Factoring Cumulative Assessment
Question 1.
Classify each polynomial by the number of terms. Then order the polynomials by degree from least to greatest.
a. -4x3
b. 6y – 3y5
c. c2 + 2 + c
d. -10d4 + 7d2
e. -5z11 + 8z12
f. 3b6 – 12b8 + 4b4
Answer:
| polynomial | Degree | Number of terms |
| -4x3 | 3 | 1 |
| 6y – 3y5 | 5 | 2 |
| c2 + 2 + c | 2 | 3 |
| -10d4 + 7d2 | 4 | 2 |
| -5z11 + 8z12 | 12 | 2 |
| 3b6 – 12b8 + 4b4 | 8 | 3 |
Question 2.
Which exponential function is increasing the fastest over the interval x = 0 to x = 2 ?

Answer:
An exponential function j models a relationship in which the dependent variable is multiplied by 6 for every 1 unit the independent variable increases. The value of the function at 0 is 2.
Option D is the correct answer.
Question 3.
Find all solutions of the equation x3 + 6x2 – 4x = 24.

Answer:
x3 + 6x2 – 4x = 24
put x = -6
(-6)³ + 6(-6)² – 4(-6) = 24
-216 + 216 + 24 = 24
24 = 24
put x = -4
(-4)³ + 6(-4)² – 4(-4) = 24
-64 + 96 + 16 = 24
48 = 24
LHS ≠ RHS
x = -2
(-2)³ + 6(-2)² – 4(-2) = 24
-8 + 24 + 8 = 24
24 = 24
LHS = RHS
x = -1
(-1)³ + 6(-1)² – 4(-1) = 24
-1 + 6 + 4 = 24
9 = 24
LHS ≠ RHS
x = 2
(2)³ + 6(2)² – 4(2) = 24
8 + 24 – 8 = 24
24 = 24
LHS = RHS
Question 4.
The table shows the distances you travel over a 6-hour period. Create an equation that models the distance traveled as a function of the number of hours.
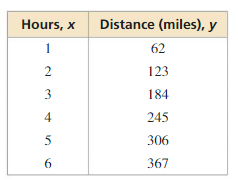
Answer:
m = y2 – y1/x2 – x1
x1 = 1, x2 = 2, y1 = 62, y2 = 123
m = 123 – 62/2 – 1
= 61
y – y1 = m(x – x1)
y – 62 = 61(x – 1)
y – 62 = 61x – 61
y = 61x – 61 + 62
y = 61x + 1
Question 5.
Consider the equation y = – \(\frac{1}{3}\)x + 2.
a. Graph the equation in a coordinate plane.
b. Does the equation represent a linear or nonlinear function?
c. Is the domain discrete or continuous?
Answer:
a.

b. It is a linear function.
c. The domain is continuous.
Question 6.
Which expressions are equivalent to -2x + 15x2 – 8?
Answer:
Given,
-2x + 15x2 – 8
We can write it as 15x² – 2x – 8
(5x – 4)(3x + 2) = 15x² – 2x – 8
(3x + 2)(5x – 4) = 15x² – 2x – 8
Question 7.
The graph shows the function f(x) = 2(3)x.
a. Is the function increasing or decreasing for increasing values of x?
b. Identify any x- and y-intercepts.
Answer:
Given,
f(x) = 2(3)x
The function is increasing.
The x-intercept does not exist as it is an increasing function.
the y-intercept is 2.
Question 8.
Which polynomial represents the product of 2x – 4 and x2 + 6x – 2?
A. 2x3 + 8x2 – 4x + 8
B. 2x3 + 8x2 – 28x + 8
C. 2x3 + 8
D. 2x3 – 24x – 2
Answer:
2x – 4 and x2 + 6x – 2
(2x – 4)(x2 + 6x – 2)
2x(x2 + 6x – 2) – 4(x2 + 6x – 2)
2x³ + 12x² – 4x – 4x² – 24x + 8
2x³ + 8x² – 28x + 8
Option B is the correct answer.
Question 9.
You are playing miniature golf on the hole shown.
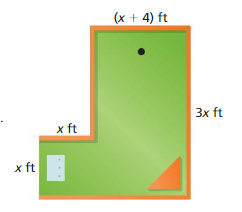
a. Write a polynomial that represents the area of the golf hole.
Answer:
length = 2x + 4
width = 3x
A = (x + 4)(3x)
A = 3x² + 12x sq. ft
Total area = x² + 3x² + 12x = 4x² + 12x
b. Write a polynomial that represents the perimeter of the golf hole.
P = x + 4 + x + 4 + 3x + 3x + x + x
P = 10x + 8 ft
c. Find the perimeter of the golf hole when the area is 216 square feet.
Answer:
4x² + 12x = 216
4x² + 12x – 216 = 0
4(x² + 3x – 54) = 0
x² + 3x – 54 = 0
(x + 9)(x – 6) = 0
x + 9 = 0 or x – 6 = 0
x = -9 or x = 6
P = 10(6) + 8
P = 60 + 8
P = 68 ft