By accessing our 180 Days of Math for Fifth Grade Answers Key Day 150 regularly, students can get better problem-solving skills.
180 Days of Math for Fifth Grade Answers Key Day 150
Directions: Solve each problem.
Question 1.
389 – 125 = __________
Answer:
Subtraction is one of the four basic arithmetic operations in mathematics. We can observe the applications of subtraction in our everyday life in different situations. For example, when we purchase fruits and vegetables for a certain amount of money say Rs. 200 and we have been given Rs. 500 note to the vendor. Now, the vendor returns the excess amount by performing subtraction such as 500 – 200 = 300. Then, the vendor will return Rs. 300.
Now we need to calculate the above-given question:
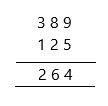
389 = Minuend; 125 = Subtrahend; 264 = Difference
Therefore, the answer is 264.
Question 2.
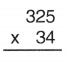
Answer:
In mathematics, multiplication is a method of finding the product of two or more numbers. It is one of the basic arithmetic operations, that we use in everyday life. The major application we can see in multiplication tables.
In arithmetic, the multiplication of two numbers represents the repeated addition of one number with respect to another. These numbers can be whole numbers, natural numbers, integers, fractions, etc. If m is multiplied by n, then it means either m is added to itself ‘n’ a number of times or vice versa.
The formula for multiplication:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
– The multiplicand is the total number of objects in each group
– A multiplier is the number of equal groups
– Product is the result of multiplication of multiplier and multiplicand
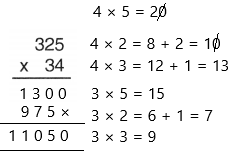
Therefore, the answer is 11050.
Question 3.
![]()
Answer:
The square root of a number is defined as the value, which gives the number when it is multiplied by itself. The radical symbol √ is used to indicate the square root. For example, √9 = 3. The radical symbol is also called a root symbol or surds. If a number is a perfect square, we can easily find the square root of the number. If the given number is not a perfect square number, the square root can be found using the long division method.
– Here we will show you how to calculate the square root of 276 using the long division method with one decimal place accuracy.

The answer is on top. The square root of 276 with one digit decimal accuracy is 16.613. Did you notice that the last two steps repeat the previous two steps? You can add decimals by simply adding more sets of 00 and repeating the last two steps over and over.
therefore, the square root of 276 is 16.613
The above-given question is 4 square root of 276 is:
We got a square root of 276 is 16.613
Now multiply 4 by 16.613
Thus, 4*16.613 is 66.452
Question 4.
How many digits are in 90,030?
Answer:
Place value in Maths describes the position or place of a digit in a number. Each digit has a place in a number. When we represent the number in general form, the position of each digit will be expanded. Those positions start from a unit place or we also call it one’s position. The order of place value of digits of a number of right to left is units, tens, hundreds, thousands, ten thousand, a hundred thousand, and so on.
The above-given number is 90,030
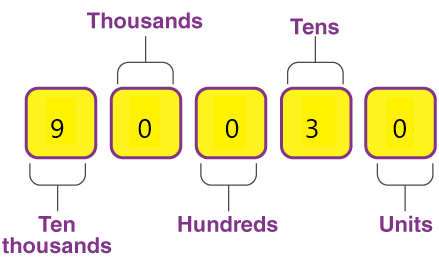
There are 5 digits.
9 is in the ten thousand places.
0 is in the thousands place.
0 is in the hundreds place
3 is in the tens place
0 is in the units place.
Question 5.
\(\frac{3}{4}\) × 32 = __________
Answer:
\(\frac{3}{4}\) can be written as: 3/4
Now we have to multiply with 32. Assume the answer be X.
X = 3/4 × 32
X = 3 × 8
X = 24
Therefore, the value of above equation is 24.
Question 6.
56 ÷ 7 – 42 ÷ 7 = __________
Answer:
The value of 56 ÷ 7 is 8
The value of 42 ÷ 7 is 6
Now subtract the values we got. Now assume the answer be X.
X = 8 – 6
x = 2.
Therefore, the answer for the above equation is 2.
Question 7.
7 × 10 = 140 ÷ ____________
Answer:
the value of 7 × 10 is 70
Let the blank be X.
7 × 10 = 140 ÷ X
70 = 140 ÷ X
Now get X to the left-hand side then the equation will be:
70 × X = 140
X = 140/70
X = 2
Now substitute the X value in the above-given equation.
7 × 10 = 140 ÷ X
7 × 10 = 140 ÷ 2
70 = 70
LHS = RHS
hence, the answer is verified.
Question 8.
What is the volume of the prism?
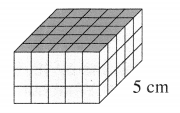
Answer:
Question 9.
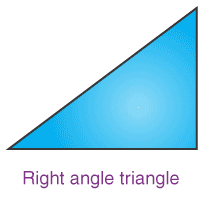
One of the angles of a triangle is 90°. What kind of triangle is it: right, isosceles, or scalene?
Answer: right angle
– If the measure of the angle between two rays is exactly equal to 90 degrees or π/2, then the angle is called a right angle.
– A right-angled triangle is a type of triangle that has one of its angles equal to 90 degrees. The other two angles sum up to 90 degrees. The sides that include the right angle are perpendicular and the base of the triangle. The third side is called the hypotenuse, which is the longest side of all three sides. The side opposite the right angle is the smallest side.
Question 10.
What is the mean of these numbers?
81, 34, 79, 52, 66
Answer:
Mean is the average of the given numbers and is calculated by dividing the sum of given numbers by the total number of numbers.
Mean = sum of observations/number of observations.
n=5
Mean = 81+34+79+52+66/5
Mean=312/5
Mean = 62.4
Therefore, the mean value is 62.4
Question 11.
These twelve marbles are put into a bag and randomly selected for a game. Colour the circles so there is a 50% probability of selecting orange, a 25% chance of selecting blue, and a 25% chance of selecting yellow.
Answer:
The number of marbles = 12
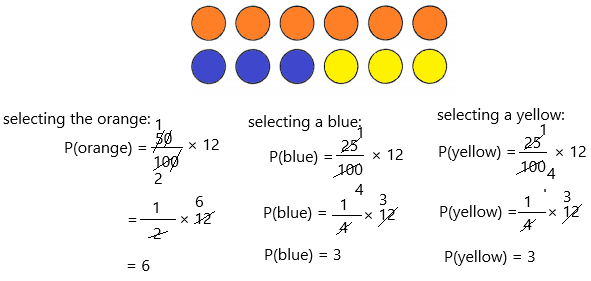
Therefore, 6 circles are orange; 3 circles are blue; 3 circles are yellow.
Question 12.
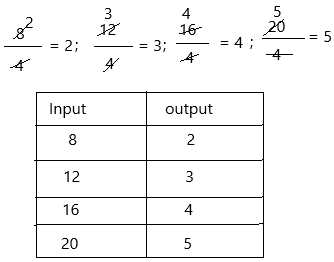
Find the rule and complete the table.
| Input | Output |
| 8 | 2 |
| 12 | 3 |
| 16 | |
| 20 |
Answer:
It is a geometric sequence.
The geometric progression is a relation between two non-zero numbers in which, after the first term, each succeeding term is found by multiplying the previous term with a fixed, non-zero number.
8, 12, 16, 20 are the above-given numbers
8, 12, 16, 20 … is a Geometric sequence because the step is divided by 4 which is the common ratio.