Quadrilateral Worksheets provided here are drafted for students in high school so that they gain adequate knowledge on several quadrilaterals such as parallelogram, rhombus, trapezium, etc. You will have problems for finding the area, perimeter, angle of Quadrilateral in the Worksheet on Quadrilaterals. Become more confident in the exam by practicing the questions on Math Quadrilaterals Worksheets on a regular basis. These worksheets are easy to use and free to download. Our Quadrilateral Worksheet with Answers is a great resource for Children in 5th Grade Math to enhance their problem-solving ability and logical skills.
Also, See:
- Perimeter of Quadrilateral
- Sum of Angles of a Quadrilateral
- Construct Different Types of Quadrilaterals
I. Fill in the blanks
1. The sum of angles of a quadrilateral is _______ degree.
2. Every square is a ________ but not every rectangle is not a _______.
3. A _____ is a quadrilateral with four congruent sides and congruent angles.
4. A Quadrilateral has ______ sides.
Solution:
1. 360
2. rectangle, square
3. Square
4. four
II. Word Problems on Quadrilateral
Example 1.
One angle of a quadrilateral is 60°and the other three angles are equal. What is the measure of each of these equal angles?
Solution:
Given,
One angle of a quadrilateral is =60°
The other three angles are equal.
We know that in a quadrilateral, the sum of the angles of a quadrilateral is 360.
Therefore, 360-60=300
The measure of each of these equal angles=300/3=100
Hence, the measure of each of these equal angles is 100.
Example 2.
Two adjacent sides AB and BC of a parallelogram ABCD are in the ratio 3:5. If the perimeter of the parallelogram is 192 cm, What is the length of AB and BC?
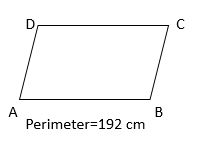
Solution:
Given,
Two adjacent sides AB and BC of a parallelogram ABCD are in the ratio of 3:5
Perimeter of the parallelogram=192 cm
Let the sides be 3x and 5x.
We know that opposite sides of the parallelogram are equal to each other.
i.e. AB=CD, BC=AD
5x+3x+5x+3x=192
16x=192
x=192/16=12
AB=3x=3(12)=36
BC=5x=5(12)=60
Hence, Length of AB and Bc are 36 cm, 60 cm.
Example 3.
If one angle of a parallelogram is 800. Find its opposite and adjacent angles of the parallelogram?
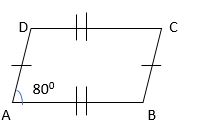
Solution:
Given,
One angle of a parallelogram=800
We know that opposite angles of a parallelogram are equal.
So the opposite angle is also 800.
Let the other two adjacent angles be x.
We also know that the sum of all angles=3600
So 80 +80 + x+x=360
160+2x=360
2x=360-160=200
x=1000
Therefore, the opposite angle and adjacent angles are 800,1000.
Example 4.
A quadrilateral has three angles equal to 60,60, and 120. Find its fourth angle?
Solution:
Given three angles of a quadrilateral are 60,60, and 120.
Let the fourth angle be x.
We know that sum of four angles=360
60+60+120+x=360
240+x=360
x=360-240=120
Hence, the fourth angle is 120.
Example 5.
What is the area of a rhombus whose perimeter is 80 cm and one of the diagonal is 30 cm?
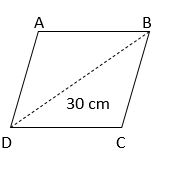
Solution:
Given,
The perimeter of the rhombus=80 cm
one of the diagonal=30 cm
Let the sides of the rhombus AB=Bc=CD=DA=xcm
Perimeter of rhombus=x +x +x +x=4x
4x=80
x=80/4=20
Therefore, All sides of the rhombus=20 cm
In △ ABD, AB=AD=20 cm
BD=30 cm
Semiperimeter=20+20+30/2=70/2=35
Area=\(\sqrt{s(s-a)(s-b)(s-c) }\)
=\(\sqrt{35(35-20)(35-20)(35-30) }\)
=\(\sqrt{ 35(15)(15)(5) }\)
=75\(\sqrt{ 7}\)
Therefore area of ABCD=2 × 75\(\sqrt{ 7}\)
=150\(\sqrt{ 7}\)
Therefore, Area of the rhombus=150\(\sqrt{ 7}\).
Example 6.
The length of the diagonals of the rhombus is 28 cm and 36 cm. Find the perimeter of the rhombus?
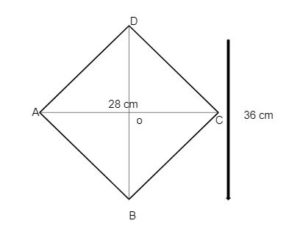
Solution:
Given,
Length of diagonals of rhombus=28 cm, 36 cm
OC=28/2=14 cm
OD=36/2=18 cm
We will find the side of the rhombus by the Pythagoras theorem.
DOC is a right-angle triangle, we know that a2+b2=c2
142+182=c2
196+324=c2
520=c2
c=22.80
The side of the rhombus is 22.80 cm
The perimeter of rhombus=4 × side of the rhombus
=4 × 22.80
=91 cm
Hence, the perimeter of the rhombus is 91 cm.
Example 7.
In a trapezium, the measurement of one parallel side is two more than the other parallel side and the height is 2 cm. The area of the trapezium is 32 cm2. Find the lengths of the two parallel sides.
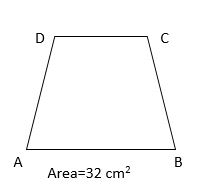
Solution:
Given,
h=2 cm
Area=32 cm2
Let a and b be the two parallel sides.
One parallel side is two more than the other.
a=b+2
Area of trapezium=32 cm2
1/2(a+b)h=32
1/2(b+2+b)2=32
2b+2=32
2b=30
b=15
a=15+2=17
Hence, the lengths of the two parallel sides are 15 cm, 17cm.
Example 8.
The perimeter of a square is 36 cm. Find the area and the length of its diagonal?
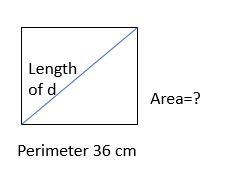
Solution:
Given,
The perimeter of a square=36 cm
4s=36
s=9 cm
Area=side2
=9 × 9=81 sq cm
Area of square = 1/2×(diagonal)²
81=1/2×(diagonal)²
(diagonal)²=81 × 2
(diagonal)²=162
diagonal=\(\sqrt{ 162 }\)
=12.72 cm
Example 9.
Find the number of sides of a regular polygon whose each exterior angle has a measure of 72 degrees.
Solution:
Let the number of sides of the polygon be n.
Sum of exterior angles=3600
Given that measure of each exterior angle is 72 degrees.
We know the formula, No. of sides × measure of each exterior angle=3600
n × 72=360
n=360/72=5
Therefore, no. of sides of a regular polygon is 5.
Example 10.
Five of the angles of a hexagon are each 1100. Calculate the measure of the sixth angle.
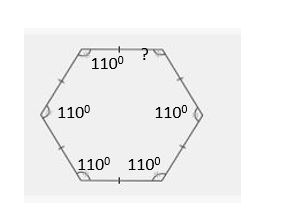
Solution:
Each of the five of the angles of a hexagon is =1100
We know that sum of all angles of hexagon=720
Let the sixth angle of hexagon=x
x+110+110+110+110+110=720
x+550=720
x=720-550
x=170
Therefore, the Sixth angle is 1700
Example 11.
The interior angle of a regular polygon is five times its exterior angle. What is the number of sides?
Solution:
Let the exterior angle be x.
Then interior angle will be 5x.
The sum of interior angles+sum of exterior angles=180°
x + 5x = 180°
x = 180/6= 30°
Since the sum of exterior angles=360°. Divide that by the exterior angle and you have the number of angles, hence the number of sides.
360÷30=12
Hence, the number of sides is 12.
Example 12.
The ratio between the interior angles and exterior angles of a regular polygon is 5:1. Find the number of sides of the polygon?
Solution:
Let interior angle and exterior angle of a polygon are 5x° and x° respectively.
We know that sum of interior and exterior angles is equal to 180°.
5x+x=180°
6x=180° => x= 30° [exterior angle is 30°]
But exterior angle = 360°/n
Therefore. 360°/n=30° => n = 360°/30°. = 12 sides.
Example 13.
In the adjoining isosceles trapezium, ABCD <A is equal to 1020. Find all the remaining angles of the trapezium?
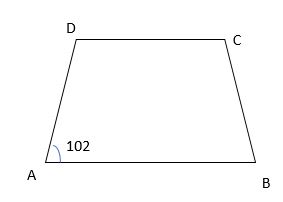
Solution:
Given,
<A=1020
Since it is an adjoining isosceles trapezium ABCD,
AB parallel to CD and BC parallel to AD
<DAB=<CBA, <ADC=<DCB
<A=<DAB=1020,<B=1020
Therefore, <CBA=102
<A+<D=1800
<D=180-102=780
<c=780
Hence,<A=1020,<B=1020,<c=780, and <D=780.
