Worksheet on Polygon and its Classification is given with various questions and hidden answers. Get the various examples on Polygon and its Classification for 7th grade math. All the students can easily be aware of the tips to solve different kinds of problems. Know the definitions of polygons, practice questions, and complete concepts related to a polygon on our website for free. Not only polygons but all the concepts of grade 7 are also given entirely for free to students. Utilize the best opportunity to learn math in an easy way by referring to our website.
Read More:
Classification of Polygon Worksheet | Types of Polygons Worksheet PDF
Check out various problems, solutions, and their solving methods on Polygon in this article. You can first try the solution on your own and verify with our solutions to know your level of practice.
Question 1.
Which of the following are polygons and Give reasons?
(i) 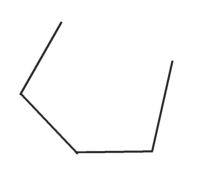 (ii)
(ii) 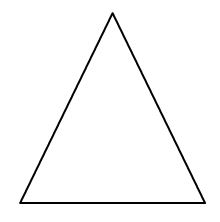 (iii)
(iii) 
Solution:
From the given images,
(i) The first image is not a closed figure. So, it is not a polygon.
(ii) The Second image is a closed figure connecting with line segments. Therefore, the image is a polygon.
(iii) Also, the third image is a closed figure connecting with line segments. Therefore, the image is a polygon.
Question 2.
How many diagonals do the below polygons have?
(a) Octagon
(b) Triangle
(c) Regular Hexagon
(d) Quadrilateral
(e) Pentagon
(f) Convex quadrilateral
Solution:
(a) Given polygon is Octagon.
The Octagon consists of 8 sides.
The formula to find the diagonal of the Octagon is n(n-3)/2 where n is the number of sides of the polygon.
Here n = 8.
Substitute 8 in the n(n-3)/2
n(n-3)/2 = 8(8 – 3)/2 = 8(5)/2 = 40/2 = 20.
Therefore, the number of diagonals in the octagon has 20.
(b) Given polygon is Triangle.
The Triangle consists of 3 sides or 3 line segments.
The formula to find the diagonal of the Triangle is n(n-3)/2 where n is the number of sides of the polygon.
Here n = 3.
Substitute 3 in the n(n-3)/2
n(n-3)/2 = 3(3 – 3)/2 = 3(0)/2 = 0.
Therefore, the number of diagonals in the Triangle is 0.
(c) Given polygon is Regular Hexagon.
The Regular Hexagon consists of 6 sides or 6 line segments.
The formula to find the diagonal of the Regular Hexagon is n(n-3)/2 where n is the number of sides of the polygon.
Here n = 6.
Substitute 6 in the n(n-3)/2
n(n-3)/2 = 6(6 – 3)/2 = 6(3)/2 = 9.
Therefore, the number of diagonals in the Regular Hexagon is 9.
(d) Given polygon is Quadrilateral.
The Quadrilateral consists of 4 sides or 4 line segments.
The formula to find the diagonal of the Quadrilateral is n(n-3)/2 where n is the number of sides of the polygon.
Here n = 4.
Substitute 4 in the n(n-3)/2
n(n-3)/2 = 4(4 – 3)/2 = 4(1)/2 = 2.
Therefore, the number of diagonals in the Quadrilateral is 2.
(e) Given polygon is Pentagon.
The Pentagon consists of 5 sides or 5 line segments.
The formula to find the diagonal of the Pentagon is n(n-3)/2 where n is the number of sides of the polygon.
Here n = 5.
Substitute 5 in the n(n-3)/2
n(n-3)/2 = 5(5 – 3)/2 = 5(2)/2 = 5.
Therefore, the number of diagonals in the Pentagon is 5.
(f) Given polygon is Convex quadrilateral.
The Convex quadrilateral consists of 4 sides or 4 line segments.
The formula to find the diagonal of the Convex quadrilateral is n(n-3)/2 where n is the number of sides of the polygon.
Here n = 4.
Substitute 4 in the n(n-3)/2
n(n-3)/2 = 4(4 – 3)/2 = 4(1)/2 = 2.
Therefore, the number of diagonals in the Convex quadrilateral is 2.
Question 3.
Draw a regular hexagon. Join any three of its vertices and draw a triangle. Name the triangle obtained.
Solution:
The regular hexagon is
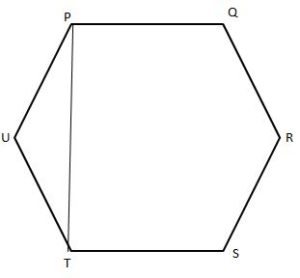
The vertices of the hexagon are P, Q, R, S, T, and U. By joining the vertices P and T, we can get a triangle of PUT.
The name of the triangle is PUT.
Question 4.
What is a regular polygon? Write the names of regular polygons having
(a) 4 sides
(b) 3 sides
(c) 6 sides
Solution:
Regular Polygon: The regular polygon consists of all equal sides and also equal angles in it. The regular polygon has three parts. They are sides, vertices, and angles (interior and exterior).
(a) The regular polygon consists of 4 sides are quadrilaterals. The quadrilaterals are closed shapes with 4 sides. Some of the quadrilaterals are
(i) square
(ii) rectangle
(iii) parallelogram
(iv) rhombus
(v) trapezium
(vi) isosceles trapezium
(vii) kite
(viii) irregular quadrilateral
(b) The regular polygon consists of 3 sides are Triangles. The Triangles are closed shapes with 3 sides. Some of the Triangles are
(i) Equilateral
(ii) Isosceles
(iii) Scalene
(c) The regular polygon consists of 6 sides are hexagon. The hexagons are closed shapes with 6 sides.
Question 5.
What can you say about the angle sum property of a convex polygon having:
(a) 6 sides
(b) 5 sides
(c) 9 sides
(d) 10 sides
Solution:
(a) Method 1: Given that the sides of the convex polygon are 6.
The total number of triangles formed by the 6 sides of a convex polygon is 6.
The sum of the angles of a triangle is equal to 180°.
It can also be written as 6 × 180° = 1080 degrees.
As we know that the angle around a point is 360∘.
The total sum of interior angle can find out by subtracting 360 degrees from 1080 degrees.
= 1080 – 360 = 720 degress.
Therefore, the angle sum of a polygon with 6 sides is 720°.
Method 2: We can use the formula to find the sum of the interior angles of a polygon is 180°(n − 2). Here n is the total number of sides.
So, n = 6.
180°(6 – 2) = 180°(4) = 720°.
(b) Given that the sides of the convex polygon are 5.
The total number of triangles formed by the 5 sides of the convex polygon is 5.
The sum of the angles of a triangle is equal to 180°.
It can also be written as 5 × 180° = 900 degrees.
As we know that the angle around a point is 360∘.
The total sum of interior angles can find out by subtracting 360 degrees from 900 degrees.
= 900 – 360 = 540 degress.
Therefore, the angle sum of a polygon with 5 sides is 540°.
(c) Given that the sides of the convex polygon are 9.
The total number of triangles formed by the 9 sides of the convex polygon is 9.
The sum of the angles of a triangle is equal to 180°.
It can also be written as 9 × 180° = 1620 degrees.
As we know that the angle around a point is 360∘.
The total sum of interior angles can find out by subtracting 360 degrees from 1620 degrees.
= 1620 – 360 = 1260 degress.
Therefore, the angle sum of a polygon with 9 sides is 1260°.
(d) Given that the sides of the convex polygon are 10.
The total number of triangles formed by the 10 sides of the convex polygon is 10.
The sum of the angles of a triangle is equal to 180°.
It can also be written as 10 × 180° = 1800 degrees.
As we know that the angle around a point is 360∘.
The total sum of interior angles can find out by subtracting 360 degrees from 1800 degrees.
= 1800 – 360 = 1440 degress.
Therefore, the angle sum of a polygon with 10 sides is 1440°.
Question 6.
Find each interior angle in a regular polygon of
(a) 6 sides
(b) 5 sides
(c) 8 sides
(d) 10 sides
Solution:
(a) The interior angle in a regular polygon consisting of 6 sides can find with the help of the formula (n−2) × 180° / n where n is the number of sides of the given polygon.
Here n = 6.
Substitute the value of the n in the (n−2) × 180° / n.
= (6 – 2)× 180° / 6 = 120°
Therefore, the interior angle of a regular polygon having 6 sides is 120°.
(b) The interior angle in a regular polygon consisting of 5 sides can find with the help of the formula (n−2) × 180° / n where n is the number of sides of the given polygon.
Here n = 5.
Substitute the value of the n in the (n−2) × 180° / n.
= (5 – 2)× 180° / 5 = 108°
Therefore, the interior angle of a regular polygon having 5 sides is 108°.
(c) The interior angle in a regular polygon consisting of 8 sides can find with the help of the formula (n−2) × 180° / n where n is the number of sides of the given polygon.
Here n = 8.
Substitute the value of the n in the (n−2) × 180° / n.
= (8 – 2)× 180° / 8 = 135°
Therefore, the interior angle of a regular polygon having 8 sides is 135°.
(d) The interior angle in a regular polygon consisting of 10 sides can find with the help of the formula (n−2) × 180° / n where n is the number of sides of the given polygon.
Here n = 10.
Substitute the value of the n in the (n−2) × 180° / n.
= (10 – 2)× 180° / 10 = 144°
Therefore, the interior angle of a regular polygon having 10 sides is 144°.
Question 7.
Find the number of sides of a polygon, the sum of whose interior angle is:
(a) 1260°
(b) 900°
(c) 1620°
(d) 540°
(e) 2160°
Solution:
(a) Given that the sum of the interior angle is 1260°.
We know that the formula to find the sum of the interior angle is (n−2) × 180° where n is the number of sides.
So, compare the given sum of the interior angle with the formula (n−2) × 180°.
(n−2) × 180° = 1260°
n−2 = 1260°/180°
n−2 = 7
n = 7 + 2
n = 9.
Therefore, the total number of sides of a polygon is 9.
(b) Given that the sum of the interior angle is 900°.
We know that the formula to find the sum of the interior angle is (n−2) × 180° where n is the number of sides.
So, compare the given sum of the interior angle with the formula (n−2) × 180°.
(n−2) × 180° = 900°
n−2 = 900°/180°
n−2 = 5
n = 5 + 2
n = 7.
Therefore, the total number of sides of a polygon is 7.
(c) Given that the sum of the interior angle is 1620°.
We know that the formula to find the sum of the interior angle is (n−2) × 180° where n is the number of sides.
So, compare the given sum of the interior angle with the formula (n−2) × 180°.
(n−2) × 180° = 1620°
n−2 = 1620°/180°
n−2 = 9
n = 9 + 2
n = 11.
Therefore, the total number of sides of a polygon is 11.
(d) Given that the sum of the interior angle is 540°.
We know that the formula to find the sum of the interior angle is (n−2) × 180° where n is the number of sides.
So, compare the given sum of the interior angle with the formula (n−2) × 180°.
(n−2) × 180° = 540°
n−2 = 540°/180°
n−2 =3
n = 3 + 2
n = 5.
Therefore, the total number of sides of a polygon is 5.
(e) Given that the sum of the interior angle is 2160°.
We know that the formula to find the sum of the interior angle is (n−2) × 180° where n is the number of sides.
So, compare the given sum of the interior angle with the formula (n−2) × 180°.
(n−2) × 180° = 2160°
n−2 = 2160°/180°
n−2 =12
n = 12 + 2
n = 14.
Therefore, the total number of sides of a polygon is 14.
Question 8.
Find the number of sides of a polygon whose each interior angle is:
(a) 164.34782°
(b) 128.5714°
(c) 90°
(d) 120°
(e) 135°
Solution:
(a) Given that each interior angle is 164.34782°.
We know that the formula to find the number of sides when each interior angle is given is (no. of sides) x (a measure of exterior angle) = 360°
The measure of exterior angle = 180° – 164.34782° = 15.65218°
(no. of sides) x (measure of exterior angle) = 360°
no. of sides = 360°/15.65218° = 23
Therefore, the total number of sides of a polygon is 23.
(b) Given that each interior angle is 128.5714°.
We know that the formula to find the number of sides when each interior angle is given is (no. of sides) x (a measure of exterior angle) = 360°
The measure of exterior angle = 180° – 128.5714° = 51.4286°
(no. of sides) x (measure of exterior angle) = 360°
no. of sides = 360°/51.4286° = 7
Therefore, the total number of sides of a polygon is 7.
(c) Given that each interior angle is 90°.
We know that the formula to find the number of sides when each interior angle is given is (no. of sides) x (a measure of exterior angle) = 360°
The measure of exterior angle = 180° – 90° = 90°
(no. of sides) x (measure of exterior angle) = 360°
no. of sides = 360°/90° = 4
Therefore, the total number of sides of a polygon is 4.
(d) Given that each interior angle is 120°.
We know that the formula to find the number of sides when each interior angle is given is (no. of sides) x (a measure of exterior angle) = 360°
The measure of exterior angle = 180° – 120° = 60°
(no. of sides) x (measure of exterior angle) = 360°
no. of sides = 360°/60° = 6
Therefore, the total number of sides of a polygon is 6.
(e) Given that each interior angle is 135°.
We know that the formula to find the number of sides when each interior angle is given is (no. of sides) x (a measure of exterior angle) = 360°
The measure of exterior angle = 180° – 135° = 45°
(no. of sides) x (measure of exterior angle) = 360°
no. of sides = 360°/45° = 8
Therefore, the total number of sides of a polygon is 8.
Question 9.
Each polygon is divided into a number of triangles. Find the number of triangles if the number of sides in a polygon is:
(a) 4
(b) 8
(c) 13
(d) 17
(e) 21
Solution:
(a) Given that the number of sides in a polygon is 4. Each polygon is divided into a number of triangles.
We know the formula to find the number of triangles in a polygon is (n – 2) where n is the number of sides.
Here, n = 4.
Substitute the value of the n in the (n−2).
= 4 – 2 = 2.
Therefore, the number of triangles if the number of sides in a polygon is 2.
(b) Given that the number of sides in a polygon is 8. Each polygon is divided into a number of triangles.
We know the formula to find the number of triangles in a polygon is (n – 2) where n is the number of sides.
Here, n = 8.
Substitute the value of the n in the (n−2).
= 8 – 2 = 6.
Therefore, the total number of sides of a polygon is 6.
(c) Given that the number of sides in a polygon is 13. Each polygon is divided into a number of triangles.
We know the formula to find the number of triangles in a polygon is (n – 2) where n is the number of sides.
Here, n = 13.
Substitute the value of the n in the (n−2).
= 13 – 2 = 11.
Therefore, the total number of sides of a polygon is 11.
(d) Given that the number of sides in a polygon is 17. Each polygon is divided into a number of triangles.
We know the formula to find the number of triangles in a polygon is (n – 2) where n is the number of sides.
Here, n = 17.
Substitute the value of the n in the (n−2).
= 17 – 2 = 15.
Therefore, the total number of sides of a polygon is 15.
(e) Given that the number of sides in a polygon is 21. Each polygon is divided into a number of triangles.
We know the formula to find the number of triangles in a polygon is (n – 2) where n is the number of sides.
Here, n = 21.
Substitute the value of the n in the (n−2).
= 21 – 2 = 19.
Therefore, the total number of sides of a polygon is 19.
Question 10.
Find the sum of the measure of interior angles of the following polygons having
(a) 9 sides
(b) 14 sides
(c) 18 sides
(d) 22 sides
Solution:
(a) Given that the polygon consists of 9 sides.
We know the formula to find the sum of the interior angles is (n−2) × 180° where n is the number of sides.
Here, n = 9.
Substitute the value of the n in the (n−2) × 180°.
= (9−2) × 180° = 7 × 180° = 1260°.
Therefore, the sum of the interior angles is 1260°.
(b) Given that the polygon consists of 14 sides.
We know the formula to find the sum of the interior angles is (n−2) × 180° where n is the number of sides.
Here, n = 14.
Substitute the value of the n in the (n−2) × 180°.
= (14−2) × 180° = 12 × 180° = 2160°.
Therefore, the sum of the interior angles is 2160°.
(c) Given that the polygon consists of 18 sides.
We know the formula to find the sum of the interior angles is (n−2) × 180° where n is the number of sides.
Here, n = 18.
Substitute the value of the n in the (n−2) × 180°.
= (18−2) × 180° = 16 × 180° = 2880°.
Therefore, the sum of the interior angles is 2880°.
(d) Given that the polygon consists of 22 sides.
We know the formula to find the sum of the interior angles is (n−2) × 180° where n is the number of sides.
Here, n = 22.
Substitute the value of the n in the (n−2) × 180°.
= (22−2) × 180° = 20× 180° = 3600°.
Therefore, the sum of the interior angles is 3600°.
Question 11.
What is Hexagon? Draw a Hexagon with diagonals?
Solution:
A hexagon is one type of polygon with 6 sides and 6 vertices.
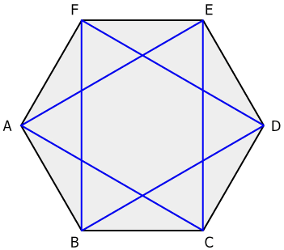
In the above figure, A, B, C, D, E, and F are the vertices of the hexagon. The diagonals are drawn from one vertex to another vertex.
