Finding Least Common Multiple and Highest Common Factor of two or more numbers and stuck at some point? Don’t bother we will assist you all throughout in finding the HCF and LCM. Practice the questions in the Worksheet on Methods of HCF and LCM and choose the method that you are comfortable with and answer the problems related easily. Download the HCF and LCM Worksheet PDF for free and solve as many problems as you can and understand the concept better.
Also, Refer:
Highest Common Factor and Least Common Multiple Methods Worksheet
Finding HCF using Factorization, Prime factorization Method, Euclid’s Algorithm
Example 1.
Find HCF of 3, 15, 21 using factorization method?
Solution:
The factors of 3 are 1,3
The factors of 15 are 1,3,5,15
The factors of 21 are 1,3,7,21
The highest common factor is 3.
Hence, the HCF of 3,15,21 is 3.
Example 2.
Find HCF of 20,30,60 by using the prime factorization method?
Solution:
Prime Factors of 20 = 2 × 2 × 5
Prime Factors of 30= 2 ×3 × 5
prime Factors of 60= 2 × 2 × 3 ×5
The highest number of occurrences of each prime number common to all is 2 × 2 ×3 ×5=60.
Therefore, HCF of 20,30,60 = 2 × 2 ×3 × 5=60
Example 3.
Find the GCF of(650,520) by using Euclid’s algorithm
Solution:
In the given numbers 650,520
subtract the smaller number from the larger number i.e. 650-520=130.
Subtract the result from a new large number i.e. 520-130=390.
Repeat the same process for every new large number and continue until you reach zero i.e.390-130=260
and then 260-130=130
130-130=0
GCF is the number before the zero results. Here it is 130.
Example 4.
Find the GCF of (420,310) by using Euclid’s algorithm
Solution:
In the given numbers 420,310
subtract the smaller number from the larger number i.e. 420-310=110.
Subtract the result from a new large number i.e. 310-110=200.
Repeat the same process for every new large number and continue until you reach zero i.e.390-130=260
and then 200-110=90
110-90=20
90-20=70
70-20=50
50-20=30
30-20=10
20-20=0
GCF is the number before the zero results. Here it is 10.
Find LCM by using Different methods
Example 5.
Find the LCM of 4,8,12 by listing the multiples?
Solution:
Multiples of 4 are 4,8,12,16,20,24,28,…..
Multiples of 8 are 8,16,24,32,40,48……
Multiples of 12 are 12,24,36,48,60,…….
The least common multiple is 24.
Therefore, the LCM of 4,8,12 is 24.
Example 6.
Find the LCM of 18,20,25 using the prime factorization method?
Solution:
Prime factors of 18 are 3 × 2 ×3
Prime factors of 20 are 2 × 2 × 5
Prime factors of 25 are 5 × 5
The LCM of 18,20,25 = 2 × 2 × 3 × 3× 5 × 5=900.
Example 7.
Find the LCM of 14,18,30 using the ladder method?
Solution:
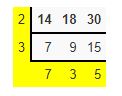
LCM=2 ×3 ×7 ×3×5=630.
Example 8.
Find the LCM of 6,12,30 by division method?
Solution:
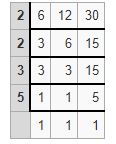
Divide the numbers by prime numbers as long as at least one of the numbers is evenly divided by a prime number.
Bring down the numbers that are not evenly divided by prime numbers.
Repeat the process until you get all ones.
For finding the lcm, multiply the prime numbers.
LCM=2 × 2 ×3 ×5=60
Example 9.
Find the LCM of (2,8,18) by using the GCF method?
Solution:
LCM(2,8,18)=LCM(LCM(2,8)18)
LCM(2,8)=(2 × 8)/GCF(2,8)
=16/2
=8
LCM(8,18)=8 ×18/GCF(8,18)
=144/2
=72
Therefore LCM(2,8,18) is 72.
Example 10.
Find the LCM of 3,18,27 by using the division method?
Solution:
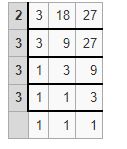
Divide the numbers by prime numbers as long as at least one of the numbers is evenly divided by a prime number.
Bring down the numbers that are not evenly divided by prime numbers.
Repeat the process until you get all ones.
For finding the lcm, multiply the prime numbers.
LCM=2 × 3 ×3 ×3=54
