Worksheet on LCM is given here. Students can get the important questions on the least common multiples on this page. Along with the problems, you can also see the solutions, steps to solve all types of LCM questions. Check out the detailed explanation on solving the L.C.M of numbers, monomials, and polynomials in the following sections. By solving all the questions of Worksheet on Least Common Multiples, you can prepare well for the exams.
You can find the lowest common multiple of numbers by finding the common prime factors, prime factorization method, division method, listing multiples, and others. Practice the problems as much as possible to clear the exam.
Also, Read: Common Factors
What is L.C.M?
The least common multiple of two integers a, b is denoted as lcm(a, b), which means the smallest positive integer that is divisible by both a and b. As the division of integers by zero is undefined, the definition has meaning only if a and b are both different from zero. The lcm is the lowest common denominator (LCD) that can be used before adding, subtracting, or comparing the fractions. The L.C.M of two or more integers can be the smallest positive integer that is divisible by all of them.
Problem 1:
Find the L.C.M of the following integers by listing their multiples.
(i) 10, 15, 35
(ii) 6, 42, 54
(iii) 16, 24, 48
Solution:
(i) The given three integers are 10, 15, 35
The process of listing multiples is
10 = 2 x 5
15 = 3 x 5
35 = 7 x 5
L.C.M = 2 x 3 x 7 x 5
= 210
Therefore, the least common multiple of 10, 15, 35 is 210.
(ii) The given three integers are 6, 42, 54
The process of listing multiples is
6 = 2 x 3
42 = 2 x 3 x 7
54 = 2 x 3 x 3 x 3
L.C.M = 2 x 3 x 3 x 3 x 7
= 378
Therefore, the least common multiple of 6, 42, 54 is 378.
(iii) The given three integers are 16, 24, 48
The process of listing multiples is
16 = 2 x 2 x 2 x 2
24 = 2 x 2 x 2 x 3
48 = 2 x 2 x 2 x 2 x 3
L.C.M = 2 x 2 x 2 x 2 x 3
= 48.
Therefore, the least common multiple of 16, 24, 48 is 48.
Problem 2:
Find the first 3 common multiples of the given using a number line.
(i) 2 and 3
(ii) 3 and 4
(iii) 9 and 12
Solution:
(i) The given numbers are 2 and 3
Multiples of 2 are 2, 4, 6, 8, 10, 12, 16, 18, 20, 22, 24, 26, 28, 30, . . .
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, . .
The first three common multiples of 2 and 3 are 6, 12, 18.
(ii) The given numbers are 3 and 4
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, . . . . .
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, . . . .
The first three common multiples of 3 and 4 are 12, 24, 36.
(iii) The given numbers are 9 and 12
Multiples of 9 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, . . .
Multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, . . . .
The first three common multiples of 9 and 12 are 36, 72, 108.
Problem 3:
Find the Lowest Common Multiple of the following by finding common prime factors.
(i) 2, 8, 10
(ii) 56, 72
(iii) 25, 30, 150
Solution:
(i) The given three integers are 2, 8, 10
Using common prime factors to get the L.C.M
2 = 2 x 1
8 = 2 x 2 x 2
10 = 2 x 5
The common factor is 2. The remaining factors are 2, 2, and 5.
So, the L.C.M = 2 x 2 x 2 x 5
= 40
Therefore, the LCM of 2, 8, 10 is 40.
(ii) The given two integers are 56, 72
Using common prime factors to get the L.C.M
56 = 2 x 2 x 2 x 7
72 = 2 x 2 x 2 x 3 x 3
The common factors are 2, 2, 2 and other factors are 7, 3, 3
So, the Least common multiple = 2 x 2 x 2 x 7 x 3 x 3
= 504
Therefore, the lowest common multiple of 56 and 72 is 504.
(iii) The given three integers are 25, 30, 150
Using common prime factors to get the L.C.M
25 = 5 x 5
30 = 5 x 2 x 3
150 = 2 x 3 x 5 x 5
The common factor is 5, remaining factors are 2, 3, 5
So, the LCM = 5 x 2 x 3 x 5
= 150
Therefore, the least common multiple of 25, 30, 150 is 150.
Problem 4:
Find the L.C.M. of the given numbers by division method.
(i) 70, 110, 150
(ii) 36, 60, 120
(iii) 21, 49, 63
Solution:
(i) The given three integers are 70, 110, 150
To find the L.C.M of three numbers using the long division method, divide the numbers by the least prime number until you left nothing common.
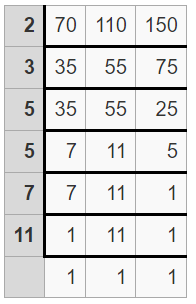
Find the product of prime numbers in the first column to get the LCM
LCM = 2 x 3 x 5 x 5 x 7 x 11
= 11,550
Therefore, LCM(70, 110, 150) = 11,550.
(ii) The given three integers are 36, 60, 120
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
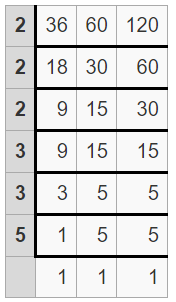
Find the product of prime numbers in the first column to get the LCM
So, LCM = 2 x 2 x 2 x 3 x 3 x 5
= 360
Therefore, LCM of 36, 60, 120 is 360.
(iii) The given three integers are 21, 49, 63
Divide your numbers by prime numbers as long as at least one of your numbers is evenly divisible by a prime number.
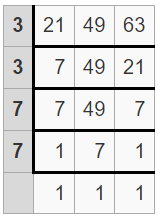
Find the product of prime numbers in the first column to get the LCM
So, least common multiple = 3 x 3 x 7 x 7
= 441
Therefore, the LCM of 21, 49, 63 si 441.
Problem 5:
Find the LCM of the given numbers by the prime factorization method.
(i) 10, 15 and 45
(ii) 36, 27 and 18
(iii) 18, 54, 72
Solution:
(i) The given three integers are 10, 15 and 45
We use prime factorization to solve LCM
Prime factorization of 10 is 2 x 5 = 2¹ x 5¹
Prime factorization of 15 is 3 x 5 = 3¹ x 5¹
Prime factorization of 45 is 3 x 3 x 5 = 3² x 5¹
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new list is 2, 3, 3, 5
Multiply these factors together to find the LCM.
LCM = 2 x 3 x 3 x 5
= 90
In exponential form: LCM = 2¹ x 3² x 5¹ = 90
Therefore, the LCM of 10, 15, and 45 is 90
(ii) The given three integers are 36, 27 and 18
We use prime factorization to find the lowest common multiple
Prime factorization of 36 = 2 x 2 x 3 x 3 = 2² x 3²
Prime factorization of 27 = 3 x 3 x 3 = 3³
Prime factorization of 18 = 2 x 3 x 3 = 2¹ x 3²
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new list is 2, 2, 3, 3, 3
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 3 x 3 x 3
= 108
In exponential form: LCM = 2² x 3³ = 108
Therefore, the LCM of 36, 27, and 18 is 108
(iii) The given three integers are 18, 54, 72
We use prime factorization to solve LCM
Prime factorization of 18 = 2 x 3 x 3= 2¹ x 3²
Prime factorization of 54 = 2 x 3 x 3 x 3 = 2¹ x 3³
Prime factorization of 72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
For each prime factor, find where it occurs most often as a factor and write it that many times in a new list.
The new list is 2, 2, 2, 3, 3, 3
Multiply these factors together to find the LCM.
LCM = 2 x 2 x 2 x 3 x 3 x 3
= 216
In exponential form: LCM = 2³ x 3³ = 216
Therefore, the LCM of 18, 54, 72 is 216.
Problem 6:
Calculate the LCM of integers using the Cake/Ladder method.
(i) 5, 27, 15
(ii) 48, 64 and 120
(iii) 12 and 20
Solution:
(i) The given three integers are 5, 27, 15
Divide your numbers by prime numbers as long as at least two numbers are evenly divisible by that prime.
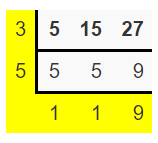
The LCM is the product of the numbers in the L shape.
Least common multiple = 3 x 5 x 9
= 135
Therefore, the lowest common multiple of 5, 27, 15 is 135.
(ii) The given three integers are 48, 64, and 120
Divide your numbers by prime numbers as long as at least two numbers are evenly divisible by that prime.
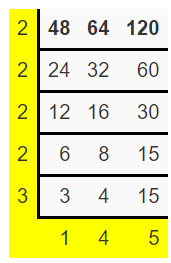
The LCM is the product of the numbers in the L shape
So, LCM = 2 x 2 x 2 x 2 x 3 x 4 x 5
= 960
Therefore, the lowest common multiple of 48, 64, and 120 is 960.
(iii) The given two integers are 12 and 20
Divide your numbers by prime numbers as long as at least two numbers are evenly divisible by that prime.
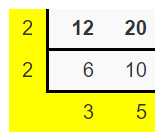
The LCM is the product of the numbers in the L shape
So, LCM = 2 x 2 x 3 x 5
= 60
Therefore, the lowest common multiple of 12, 20 is 60.
Problem 7:
Calculate the least common multiple of numbers using the G.C.F method.
(i) 49, 14, 70
(ii) 84, 90
(iii) 10, 25, 60
Solution:
(i) The given integers are 49, 14, 70
LCM(14, 49, 70) = LCM( LCM(14, 49), 70 )
L.C.M (14, 49) = \(\frac { 14 x 49 }{ G.C.F(14, 49) } \)
= \(\frac { 686 }{ 7 } \)
= 98
LCM( LCM(14, 49), 70 ) = LCM(98, 70)
= \(\frac { 98 x 70 }{ G.C.F(98, 70) } \)
= \(\frac { 6860 }{ 14 } \)
= 490
Therefore, LCM(14, 49, 70) = 490
(ii) The given integers are 84, 90
LCM of 84, 90 = \(\frac { 84 x 90 }{ G.C.F(84, 90) } \)
= \(\frac { 7560 }{ 6 } \)
= 1260
Therefore, LCM(84, 90) = 1260.
(iii) The given numbers are 10, 25, 60
LCM(10, 25, 60) = LCM( LCM(10, 25), 60 )
LCM(10, 25) = \(\frac { 10 x 25 }{ G.C.F(10, 25) } \)
= \(\frac { 250 }{ 5 } \)
= 50
LCM(10, 25, 60) = LCM(50, 60) = \(\frac { 50 x 60 }{ G.C.F(50, 60) } \)
= \(\frac { 3000 }{ 10 } \)
= 300
Therefore, LCM(10, 25, 60) = 300.
Problem 8:
Find the lowest number which is less by 2 to be divided by 56 and 98 exactly.
Solution:
Given that,
A number is less by 2 to be divided by 56 and 98 exactly
Let us take the lowest number as x
x is less by 2 to be divided by 56 and 98 exactly
So, x + 2 divided by 56 and 98 exactly
x + 2 is LCM of 56, 98
56 = 2 x 2 x 2 x 7
98 = 2 x 7 x 7
LCM = 2 x 2 x 2 x 7 x 7
= 392
So, x + 2 = 392
x = 392 – 2
x = 390
Therefore, the lowest number which is less by 2 to be divided by 56 and 98 exactly is 390
Problem 9:
The H.C.F. two numbers are 6 and their L.C.M. is 36. If one of the numbers is 18, find the other number.
Solution:
Given that,
H.C.F. two numbers = 6
L.C.M. of two numbers = 36
One number = 18
Let us consider the second number is y
x * y = LCM x HCF
18 x y = 36 x 6
18y = 216
y = \(\frac { 216 }{ 18 } \)
y = 12
Therefore, the other number is 12.
Problem 10:
The product of two numbers is 144. If the L.C.M. of these numbers is 12, find their H.C.F.
Solution:
Given that,
Product of two numbers = 144
LCM of two numbers = 12
Let us take two numbers as a, b
Then a x b = HCF x LCM
144 = HCF x 12
HCF = \(\frac { 144 }{ 12 } \)
= 12
Therefore, the highest common factor is 12.
Problem 11:
Find the LCm of monomials 4mn, 10n
Solution:
Numeral coefficients = 4 , 10
4 = 2 x 2, 10 = 2 x 5
LCM of numeral coefficients = 2 x 2 x 5 = 20
Literal coefficients = mn, n
L.C.M of mn, n = mn
Therefore, LCM(4mn, 10n) = 20mn
Problem 12:
Find the LCM of polynomials x² – 5², (x + 5)²
Solution:
First polynomial = x² – 2²
= (x – 5) (x + 5)
Second polynomial = (x + 5)²
= (x + 5) (x + 5)
In both the polynomials, the common factors are (x + 5), the extra common factor of the first polynomial (x – 5), the second polynomial is (x + 5).
Therefore, required the least common multiple = (x + 5) (x + 5) (x – 5).
