Quick Lessons on HCF and LCM provided with step-by-step solutions help students to gain complete knowledge on the concepts. Numerous Practice Worksheets on HCF and LCM will assist you in learning different methods of finding the highest common factor, least common multiple, finding HCF when LCM is given, and vice versa.
Solving the LCM and HCF Questions available in LCM and HCF Worksheet will enrich your subject knowledge, improves math skills in a fun and interactive manner. You can download, print, and share this handy Worksheet on H.C.F and L.C.M for free and help them learn how to find LCM and HCF using various methods like cake/ladder method, division method, listing multiples, factorization, prime factorization, etc.
Also, Refer:
- Relationship between H.C.F. and L.C.M
- Method of H.C.F.
- Method of L.C.M.
- Worksheet on Methods of H.C.F.and L.C.M.
LCM and HCF Questions with Answers
Example 1.
Find the highest common factors of the following by factorization?
(i) 28, 36,12
(ii) 120,68
(iii) 124, 78, 116
(iv) 1228, 386
Solution:
(i) 28, 36,12
The factors of 28 are 1,2,4,7,14,28.
The factors of 36 are 1,2,3,4,6,9,12,18,36.
The factors of 12 are 1,2,3,4,6,12.
4 is the highest common factor.
Hence, HCF is 4.
(ii) 120, 68
The factors of 120 are 1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120.
The factors of 68 are 1,2,4,17,34,68.
Hence,4 is the highest common factor.
(iii) 124, 78, 116
The factors of 124 are 1,2,4,31,62,124.
The factors of 78 are 1,2,3,6,13,26,39,78.
The factors of 116 are 1,2,4,29,58,116.
Hence, 2 is the highest common factor.
(iv) 1228,386
The factors of 1228 are 1,2,4,307,614,1228
The factors of 386 are 1,2,193,386
Hence, 2 is the greatest common factor.
Example 2.
(i) Find the HCF of 45, 120 by long division method?
(ii) Find the HCF of 150, 180 by long division method?
(iii) Find the HCF of 25,34,18 by long division method?
(iv) Find the HCF of 100, 30 by the long division method?
Solution:
1. First, Take the largest number 120 as a dividend and the smallest number 45 as the divisor.
2. Take divisor as the new dividend and remainder as the new divisor i.e. divide the first divisor(45) by the first remainder(30).
3. Continue the process until the remainder is zero and the last divisor will be the HCF of the given numbers.
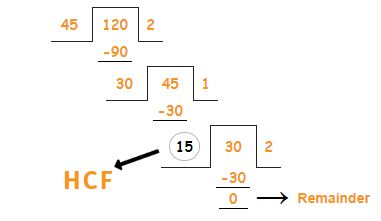
Hence, 15 is the HCF of 45,120.
(ii)
1. First, Consider the largest number 180 as a dividend and the smallest number 150 as the divisor.
2. Consider the divisor as the new dividend and the remainder as the new divisor i.e. divide the first divisor(150) by the first remainder(30).
3. Continue the procedure until the remainder is zero and the last divisor will be the HCF of the given numbers.
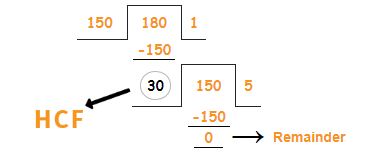
Hence, 30 is the HCF of 150,180.
(iii)
1. First, take the largest number 34 as a dividend and the smallest number 18 as the divisor.
2. Take divisor as the new dividend and remainder as the new divisor i.e. divide the first divisor(18) by the first remainder(16).
3. Continue the process until the remainder is zero and the last divisor will be the HCF of the given numbers.
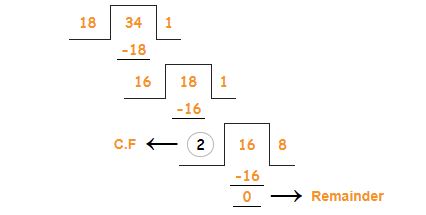
Now take the remaining value 25 as a dividend and 2 HCF of 134,325 as of the divisor.
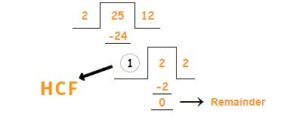
Hence, HCF of 325,134,208 is 1.
(iv)
First, take the largest number 100 as a dividend and the smallest number 30 as the divisor.
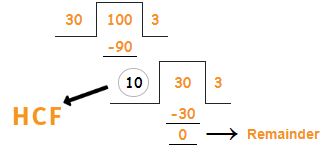
Therefore, HCF of 100,30 is 10.
Example 3.
Find the LCM of 18, 24, 32 by using the Cake/Ladder method?
Solution:
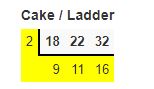
LCM=2 × 9 × 11× 16=3168
Hence,LCM of 18,24,32 is 3168.
Example 4.
Find the LCM of 30,48,55 by using the Cake/Ladder method?
Solution:
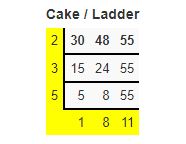
LCM=2 ×3 × 5 ×1 × 8 × 11=2640
Hence, LCM of 30, 48, 55 is 2640.
Example 5.
Find the LCM of 420,505 by using the Cake/Ladder method?
Solution:

LCM is 5 × 84 ×101=42,420
Hence, LCM of 420,505 is 42,420.
Practice Math Online with Unlimited Questions provided in 5th Grade Math Activity Sheets and become a blossoming mathematician in no time.
Example 6.
Find the LCM of 24,34,54 by using the Cake/Ladder method?
Solution:
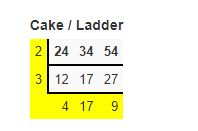
LCM is 2 × 3 × 4 × 17 × 9=3672
Hence Lcm of 24,34,54 is 3672.
Example 7.
The LCM of the two numbers is 462. If the product of two numbers is 924. Find their HCF?
Solution:
Given,
Lcm of two numbers=462
Product of two numbers=924
We know that product of two numbers= LCM × HCF
924=462 × HCF
HCF=924/462=2
Therefore, HCF is 2.
Example 8.
The HCF of the two numbers is 4. If the product of two numbers is 3264. Find their LCM?
Solution:
Given,
HCF of two numbers=4
product of two numbers=3264
We know that product of two numbers= LCM × HCF
3264=LCM × 4
LCM=3264/4=816
Therefore, LCM is 816.
Example 9.
If HCF and LCM of two numbers are 10 and 280. If one of the numbers is 40, Find the other number?
Solution:
Given,
HCF=10
LCM=280
One of the number=40
Let the other number=x
We know that product of two numbers=LCM × HCF
x . 40=280 × 10
x.40=2800
x=2800 ÷40=70
Hence, the other number is 70.
Example 10.
Find the HCF of 20,80 by prime factorization method?
Solution:
prime factorization of 20 is 2 × 2 ×5
prime factorization of 80 is 2 × 2 × 2 × 2 × 5
HCF is 2 × 2 ×5=20
Hence, HCF of 20,80 is 20.
Example 11.
Find the HCF of 10,40 by factorization method?
Solution:
factors of 10 are 1,2,5,10
factors of 40 are 1,2,4,5,8,10,20,40
Here the highest common factor is 10
Hence, HCF is 10.
Example 12.
Find the LCM of 27,33 by using the prime factorization LCM method.
Solution:
27= 3×3×3=33
33=3 × 11
LCM=33 × 11
= 27 × 11
=297
Therefore, the LCM of 27,33 is 297.
Example 13.
Find the LCM of 15,25 by using the listing multiples method?
Solution:
Multiples of 15 are 15,30,45,60,75,90,105
Multiples of 25 are 25,50,75,100,125
Here the least common multiple is 75
Hence, LCM of 15,25 is 75.
Example 14.
Find the LCM of 13,15 by division table method?
Solution:
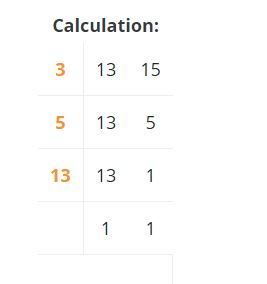
LCM is 3 × 5 × 13 =195
Hence, LCM of 13,15 is 195.
