Are you looking for help on the concept of finding the square area? If so, you have arrived at the right place that provides you complete knowledge on how to find the area of a square and its formula. Area of a Square Word Problems provided here include questions on finding areas when sides are given.
One simple logic that you need to keep in mind while solving the area of square problems is that you need to have sides of the same unit of length. If not, convert them into the same units of length and apply the formula. Start solving the area of square problems over here and cross-check your solutions with ours.
Read More:
Area of a Square Questions and Answers
Example 1.
The area of the square is 9 sq cm. Find the side of the square?
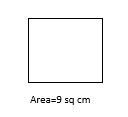
Solution:
Area of the square=9
side of the square=\(\sqrt{9 }\)
=3
Hence, side of the square=3.
Example 2.
The perimeter of the square is 32 cm. Find the area of the square?

Solution:
The perimeter of the square=32
4 a=32
a=32/4=8
Therefore, the area of the square is 8.
Example 3.
The side of the square is 7 cm. Find the area of the square?
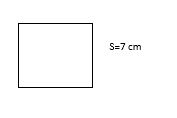
Solution:
The side of the square=7
Area of the square=72=49
Hence, the area of the square=49.
Example 4.
A square and a rectangle have the same area. The rectangle has a length of 9 cm and a width of 4 cm. Find the side of the square and its area?
Solution:
Length of the rectangle=9 cm
width of the rectangle=4 cm
Area of rectangle=9 × 4=36
Since the area of the rectangle and square are equal, the area of the square=36
Side of the square=\(\sqrt{36 }\)
=6
Hence the side of a square is 6 and the area of the square is 36.
Example 5.
The side of the square is 3 cm. If its side is doubled, how many times is the area of the new square bigger than the area of the older square?
Solution:
The side of the square=3 cm
The area of the old square=32=9
The area of the new square=62=36
The area is 4 times bigger.
Example 6.
In a square, if the length of each diagonal is 2 cm. Find its area?
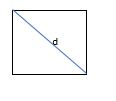
Solution:
Length of each diagonal=2
Area of the square=1/2 d2
=1/2(2)2
=1/2(4)
=4/2=2
Hence, the area of the square=2 cm.
Example 7.
If the length of diagonals of two squares is in the ratio 2:7. Find the ratio of their areas?
Solution:
let the diagonals of two squares be 2x, 7x.
Area of first square=1/2(2x)2
=1/24x2
=4x2/2
Area of the second square=1/2(7x)2
=1/249 x2
=49 x2/2
The ratio of areas=4x2/2: 49 x2/2
Multiply each term of a ratio by 2.
4x2:49 x2
Divide each term by x2
=4:49
Hence, the ratio of the squares=4:49
Example 8.
Find the area of the floor of the square-shaped room which is made up of 150 square tiles of side 20 inches?
Solution:
Area of the square tile=20 ×20=400 sq inches
As the floor is occupied by 150 square tiles, An Area of 150 square tiles=150 × 400
=60,000 sq inches
Therefore, the area of the floor is 60,000 sq inches.
Example 9.
How many squares with the side of 3 cm cover the surface of a rectangle with a length of 27 cm and a width of 10 cm?
Solution:
The area of the square=32=9 sq cm
The length of the rectangle=27 cm
the width of the rectangle=10 cm
The area of the rectangle=27 × 10=270 sq cm
The no. of squares cover the surface of rectangle=270/9=30
Hence, 30 squares are required to cover the surface of the rectangle.
Example 10.
Find the no. of square tiles with the side of 5 cm required for covering the floor of rectangular shape which is of length 25 cm and a width 10 cm?
Solution:
The area of the square tiles=52=25 sq cm
The length of the floor=25 cm
the width of the floor=10 cm
The area of the floor=25 × 10=250 sq cm
The no. of squares cover the surface of rectangle=250/25=10
Hence, 10 squares are required to cover the surface of the rectangle.
