If a triangle and parallelogram having the same base and between the same parallels, then the area of the triangle is equal to half the area of the parallelogram. Get the example problems and solutions on Triangle and Parallelogram on the Same Base and between Same Parallels. Also, find the relationship between them in the following sections explained step by step.
Proof for Area of Triangle Equal to Half of the Parallelogram having the Same Base
In the following figure, parallelogram ABCD and ∆ABD are on the same base AB and between the same parallels AF and DC. Get the area of the triangle ABD and area of the parallelogram ABCD and check their areas.

Area of the parallelogram ABCD = base x height
= AB x CF
Here, CF and DE area parallel lines CF = DE.
Area of the parallelogram = AB x DE = AB x CF.
Area of △ ABD = 1/2 x base x height
= 1/2 x AB x DE
= 1/2 x Area of the parallelogram ABCD
Therefore, Area of the parallelogram ABCD = 1/2 x Area of △ ABD
Hence proved.
Here are various case studies for the area of the parallelogram is half of the area of the triangle when they lie on the same base.
1. When a triangle and a parallelogram lies on the same base and have the same altitude, then the area of the triangle is equal to half of the parallelogram.
2. If they lie between the same parallels and have the same altitude, then the area of the triangle is equal to half of the area of the parallelogram.
3. When the triangle and rectangle have the same base and between the same parallels, then the area of the triangle is half of the area of the rectangle.
Example Questions for Triangle and Parallelogram on Same Base and between Same Parallels
Example 1:
∆ ABD and parallelogram ABCD are on the same base AB. If the base and altitude of the parallelogram are 10 cm and 6 cm, find the area of the triangle.
Solution:
Given that,
Base of the parallelogram = 10 cm
Altitude of the parallelogram = 6 cm
Area of the parallelogram = base x altitude
= 10 x 6 = 60 cm²
We know that when a triangle and parallelogram having the same base and between the same parallels then the area of the triangle is equal to half of the area of the parallelogram.
So, area of △ ABD = 1/2x Area of the parallelogram ABCD
= 1/2 x 60 = 30 cm²
Therefore, triangle area is 30 cm².
Example 2:
∆ ABD and parallelogram ABCD are on the same base AB. If the base and height of the triangle is 16 cm and 12 cm, find the area of the parallelogram.
Solution:
Given that,
The base length of the triangle = 16 cm
Height of the triangle = 12 cm
Area of ∆ ABD = 1/2 x base x height
= 1/2 x 16 x 12
= 1/2 x 192 = 96 cm²
We know that when a triangle and parallelogram having the same base and between the same parallels then the area of the parallelogram is equal to double the area of the parallelogram.
Area of the parallelogram ABCD = 2 x Area of ∆ ABD
= 2 x 96 = 192 cm²
Therefore, parallelogram area is 192 cm².
Example 3:
In the adjacent figure, BCDE is a rectangle and ABC is a triangle show that area of the triangle ABC is equal to half of the area of the rectangle BCDE.
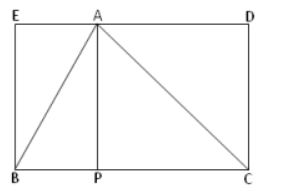
Solution:
Given that,
Triangle ABC and rectangle BCDE lies on the same base BC and between the same parallels BC and ED>
Area of triangle ABC = 1/2 x base x height
= 1/2 x BC x AP
AP and Cd are parallel lines and having the same length. So, AP = CD.
△ ABC area = 1/2 x BC x AP = 1/2 x BC x CD
Area of the rectangle = length x breadth
= BC x CD
= 1/2 x Area of △ ABC.
Therefore, the Area of the rectangle BCDE = 1/2 x Area of △ ABC
Hence, shown.