Subtraction with Decomposition 2-Digit Number from 2-Digit Number is the process of borrowing a digit from ten’s place digit to finish the subtraction. Subtraction of 2-Digit Number from 2-Digit Number with Regrouping is clearly explained in this article with the examples and activities. Follow every step of this article to learn subtraction with regrouping or decomposing easily and simply.
Also, Read:
- Subtraction without Decomposition (2-Digit Number from 2-Digit Number)
- Subtraction with Regrouping
- Subtracting 2-digit Numbers with Borrowing
How to Subtract 2 Digit Numbers with Decomposition?
Check out how to Subtract 2-Digit Numbers from 2-Digit Numbers with Regrouping. We have given the steps for subtracting 2-digit numbers with regrouping.
(i) Write down the given 2-digit numbers.
(ii) Compare the numbers and find the large number and also the small number.
(iii) Place the large number on the top and the small number below the large number.
(iv) Begin your subtraction from one’s place digits column.
(v) If the minuend one’s place digit is less than the subtrahend one’s place digit, then borrow the number by taking the value from tens place.
(vi) Then subtract the one’s place digits column and note down the number.
(vii) Reduce one number in ten’s place digit and perform the subtraction operation.
(viii) Finally, note down the answer.
Subtraction of 2 Digit Numbers with Decomposing or Borrowing
Example 1.
Subtract 35 from 62.
Solution:
The given numbers are 35 and 62.
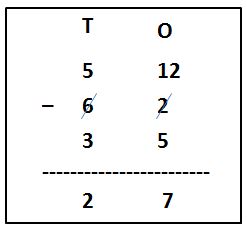
(i) Compare the given numbers. 62 is the greater number. 26 is a small number.
(ii) Subtract one’s place digits. Subtract 5 from 2. 2 is smaller than 5. Therefore, borrow 10 from ten’s place digit. Now 2 becomes 12.
(iii) Subtract 5 from 12. 12 – 5 = 7.
(iv) Reduce the number 6 to one digit i.e, 5.
(v) Now, subtract ten’s place digits. Subtract 3 from 5. 5 – 3 = 2. Place 2 in the ten’s column as shown in the figure.
(vi) Finally, the difference of 62 – 35 = 27.
Example 2.
Subtract 28 from 71.
Solution:
The given numbers are 28 and 71.
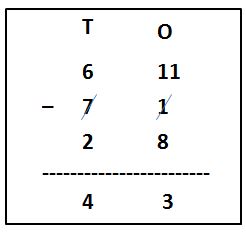
(i) Compare the given numbers. 71 is the greater number. 28 is a small number.
(ii) Subtract one’s place digits. Subtract 8 from 1. 1 is smaller than 8. Therefore, borrow 10 from ten’s place digit. Now 1 becomes 11.
(iii) Subtract 8 from 11. 11 – 8 = 3.
(iv) Reduce the number 7 to one digit i.e, 6.
(v) Now, subtract ten’s place digits. Subtract 2 from 6. 6 – 2 = 4. Place 4 in the ten’s column as shown in the figure.
(vi) Finally, the difference of 71 – 28 = 43.
Example 3.
Subtract 42 from 61.
Solution:
The given numbers are 42 and 61.
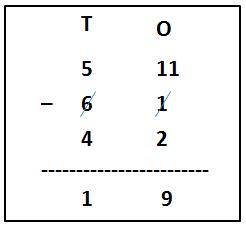
(i) Compare the given numbers. 61 is the greater number. 42 is a small number.
(ii) Subtract one’s place digits. Subtract 2 from 1. 1 is smaller than 2. Therefore, borrow 10 from ten’s place digit. Now 1 becomes 11.
(iii) Subtract 2 from 11. 11 – 2 = 9.
(iv) Reduce the number 6 to one digit i.e, 5.
(v) Now, subtract ten’s place digits. Subtract 4 from 5. 5 – 4 = 1. Place 1 in the ten’s column as shown in the figure.
(vi) Finally, the difference of 61 – 42 = 19.
FAQ’s on Subtraction of Two-Digit Numbers with Regrouping
1. Is borrowing necessary for every subtraction problem?
No, not every problem needs the borrowing of numbers.
2. What is subtraction with regrouping?
The subtraction with regrouping takes place when the minuend one’s place digit is less than the subtrahend one’s place digit.
3. How do you borrow using subtraction?
If the minuend one’s place digit is less than the subtrahend one’s place digit, then we will borrow 10 from ten’s digit number to subtract the one’s digit numbers.
4. What is the subtraction of 24 – 17?
The subtraction of 24 – 17 is 7.
