The solution to the simultaneous linear equations can be obtained by using the substitution method. It is one of the categories of the algebraic methods that give solution for system of linear equations. In this page, you will learn about substitution method definition, and how to solve equations using substitution method with example questions.
What is meant by Substitution Method?
The substitution method is one among the algebraic methods that help you to solve the simultaneous equations. As the word substitution says that, the value of one variable from one equation is substituted in the other equation. So, a pair of linear equations gets transformed into one linear equation in one variable. Later, solve the obtained equation to get the solution.
Substitution Method for Solving System of Linear Equations
For instance, the simultaneous equations with two variables can be solved using the below mentioned detailed steps. Follow them and find the solution of a system of linear equations easily.
- Simplify the given equations by expanding the paranthesis.
- Find the value of one variable in terms of the second variable from any of the given equations.
- Substitute this variable value in other equations.
- Solve the equation and get the value of one of the variables.
- Substitute that value in any one of the equations to find the value of another variable.
General Solution using the Substitution Method
Let us take two linear equations
ax + by = c —— (i)
dx + ey = f ——- (ii)
Express y in terms of x
From equation (i), we get
by = c – ax
y = (c – ax) / b
Substitute the obtained value of y in equation (ii), we get
dx + [e(c – ax)] / b = f
On simplifying this equation,
dx + (ec – aex)/b = f
dx + ec/b – aex/b = f
dx – aex/b = f – ec/b
x(d – ae/b) = (bf – ec)/b
x = [(bf – ec)/b] / [(db – ae)/b]
x = (bf – ec) / (bd – ae)
Putting the value of x in equation (i)
a[(bf – ec) / (bd – ae)] + by = c
[(abf – ace)/(bd – ae)] + by = c
by = c – [(abf – ace)/(bd – ae)]
y = {c – [(abf – ace)/(bd – ae)]} / b
y = [bc(bd – ae) – (abf – ace)] / b
Therefore, solution set is x = (bf – ec) / (bd – ae), y = [bc(bd – ae) – (abf – ace)] / b.
Substitution Method Examples with Answers
Example 1.
Solve the equations 3x + 2y = 7, 5x – 3y = 37 by substitution method?
Solution:
Given simultaneous equations are
3x + 2y = 7 ——- (i)
5x – 3y = 37 ——- (ii)
From equation (i) 3x + 2y = 7, express y in terms of x
From equation (i) 3x + 2y = 7, we get;
2y = 7 – 3x
Therefore, y = (7 – 3x) / 2
Substitute the obtained value of y in equation (ii),
By putting y = (7 – 3x) / 2 in equation (ii) 5x – 3y = 37, we get
5x – 3[(7 – 3x) / 2] = 37
5x – (21 – 9x)/2 = 37
5x – 21/2 + 9x/2 = 37
5x + 9x/2 = 37 + 21/2
(10x + 9x)/2 = (74 + 21)/2
19x = 95
x = 95/19
x = 5
Therefore, x = 5
Putting the value of x in equation (ii),
Subsutitute x = 5 in 5x – 3y = 37
5(5) – 3y = 37
25 – 3y = 37
25 – 37 = 3y
-12 = 3y
y = -12/3
y = -4
Therefore, x= 5 and y = -4 is the solution for the system of linear equations 3x + 2y = 7, 5x – 3y = 37.
Example 2.
Solve the simultaneous equations 3x + y = 9, 5x + 4y = 22 using the substitution method?
Solution:
Given system of linear equations are,
3x + y = 9 —— (i)
5x + 4y = 22 —— (ii)
Express y in terms of x
From equation (i), we get
y = 9 – 3x
Substituting y = 9 – 3x in equation (ii), we get
5x + 4(9 – 3x) = 22
5x + 36 – 12x = 22
36 – 7x = 22
36 – 22 = 7x
7x = 14
x = 14/7
x = 2
Putting x = 2 in equation (i), we get
3(2) + y = 9
6 + y = 9
y = 9 – 6
y = 3
Therefore, x = 2, y = 3 is the solution for the linear equations 3x + y = 9, 5x + 4y = 22.
Example 3.
Solve the system of linear equations x – 2y = 8, x + y = 5 by the method of substitution?
Solution:
Given simultaneous linear equations are
x – 2y = 8 —— (i)
x + y = 5 ——- (ii)
Express x in terms of y
From equation (i) we get
x = 8 + 2y
Substitute x = 8 + 2y in equation (ii)
8 + 2y + y = 5
8 + 3y = 5
3y = 5 – 8
3y = -3
y = -3/3
y = -1
Putting y = -1 in equation (i) we get
x – 2(-1) = 8
x + 2 = 8
x = 8 – 2
x = 6
Therefore, x = 6, y = -1 is the solution for the linear equations x – 2y = 8, x + y = 5.
Example 4.
Solve the pair of equations 2x + 3y = 9, x = 3 + y using the substitution method?
Solution:
Given system of linear equations are
2x + 3y = 9 —- (i)
x = 3 + y —— (ii)
Substitute x = 3 + y in the equation (i)
2(3 + y) + 3y = 9
6 + 2y + 3y = 9
6 + 5y = 9
5y = 9 – 6
5y = 3
y = 3/5
Put y = 3/5 in equation (ii)
x = 3 + 3/5
x = (15 + 3)/5
x = 18/5
Therefore, x = 18/5, y = 3/5 is the solution for the equations 2x + 3y = 9, x = 3 + y.
SEO Title: Substitution Method for Solving System of Linear Equations Examples
Meta Description: Use the Substitution Method for Solving the Simultaneous Linear Equations easily. Get Substitution Method Steps explained in detail with Example Problems.
Cross-Multiplication Method to Solve System of Linear Equations | Cross Multiplication Method Examples
Cross multiplication method is used to solve a pair of simultaneous linear equations in two variables. This method helps you to find the accurate values of variables easily. It is applicable only when we have two linear equations in two variables. Get the steps to solve the system of linear equations with the cross multiplication method in the following sections. Also, check out the solved examples for a better understanding of the concept.
Cross Multiplication Method for Solving Pair of Linear Equations
Follow the easy and simple guidelines listed below while solving Pair of Linear Equations. They are in the following fashion
- Observe the given pair of linear equations and transpose them in the form of ax + by + c = 0
- And represent them as the coefficient constant of term x, the coefficient constant of term y, coefficient of x, and coefficient of y.
- Cross multiply those constants.
- Express the cross multiplicands of x, y, and constants under x, y, and 1.
- Equate them to find the values of x, y.
Check out the derivation to get more details about the Cross-Multiplication Method.
General Solution Using the Method of Cross-Multiplication
Let the pair of linear equations in two variables are
a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0
For solving these linear equations follow the below included steps
Given simultaneous linear equations in two variables are
a₁x + b₁y + c₁ = 0 ——- (i)
a₂x + b₂y + c₂ = 0 ——– (ii)
Multiply equation (i) by b₂ and equation (ii) by b₁.
b₂ (a₁x + b₁y + c₁ = 0)
b₂ (a₁x + b₁y + c₁) = b₂ x 0
a₁b₂x + b₁b₂y + b₂c₁ = 0 ——- (iii)
b₁ (a₂x + b₂y + c₂ = 0)
b₁ (a₂x + b₂y + c₂) = b₁ x 0
a₂b₁x + b₂b₁y + c₂b₁ = 0 —- (iv)
Subtract equation (iv) from equation (iii)
[a₁b₂x + b₁b₂y + b₂c₁ = 0] – [a₂b₁x + b₂b₁y + c₂b₁ = 0]
[a₁b₂x + b₁b₂y + b₂c₁] – [a₂b₁x + b₂b₁y + c₂b₁] = 0
a₁b₂x + b₁b₂y + b₂c₁ – a₂b₁x – b₂b₁y – c₂b₁ = 0
x(a₁b₂ – a₂b₁) + b₂c₁ – c₂b₁ = 0
x(a₁b₂ – a₂b₁) = c₂b₁ – b₂c₁
x = (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁)
Substitute x = (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) in equation (i)
a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) + b₁y + c₁ = 0
b₁y = -a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) – c₁
y = (-a₁(c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) – c₁) / b₁
y = (c₁a₂ – c₂a₁) / (b₂a₁ – b₁a₂)
The solution of the equations is
x / (c₂b₁ – b₂c₁) / (a₁b₂ – a₂b₁) = y / (c₁a₂ – c₂a₁) / (b₂a₁ – b₁a₂) = 1/(b₂a₁ – b₁a₂)
The above method is called Cross-Multiplication Methos as it uses cross-multiplication technique.
You can also represent the cross-multiplication as the following diagram.
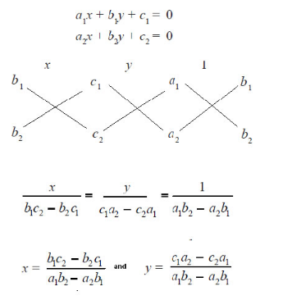
Cross Multiplication Method Examples
Example 1.
Solve the linear equations x + y = 5, x – y = 3 by using the cross multiplication method?
Solution:
Given system of linear equations are
x + y = 5
x – y = 3
On transposition, we get
x + y – 5 = 0
x – y – 3 = 0
Writing the co-efficient in the following way, we get:
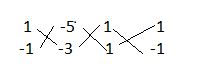
By cross-multiplication method:
x/[(1(-3) – (-1)(-5)] = y/[(-5)1 – 1(-3)] = 1//[1(-1) – 1(1)]
x/(-3 – 5) = y/(-5 + 3) = 1/(-1 – 1)
x/(-8) = y/(-2) = 1/(-2)
x/(-8) = 1/(-2), y/(-2) = 1/(-2)
x/8 = 1/2, y/2 = 1/2
x = 8/2, y = 2/2
x = 4, y = 1
Therefore, required solution is x = 4, y = 1.
Example 2.
Solve the simultaneous linear equations 3x – 4y = 0, 9x – 8y = 12 by the method of cross-multiplication?
Solution:
Given simultaneous equations are,
3x – 4y = 0
9x – 8y = 12
On transposition, we get
3x – 4y = 0 ——– (i)
9x – 8y – 12 = 0 ———- (ii)
Multiply equation (i) by -8 and equation (ii) by -4.
-8(3x – 4y) = 0 x -8
-24x + 32y = 0 —— (iii)
-4(9x – 8y – 12) = 0 x -4
-36x + 32y + 48 = 0 ——- (iv)
Subtract equation (iv) from equation (iii)
[-24x + 32y = 0] – [-36x + 32y + 48 = 0]
-24x + 32y – (-36x + 32y + 48) = 0
-24x + 32y + 36x – 32y – 48 = 0
12x – 48 = 0
12x = 48
x = 48/12
x = 4
Substitute x = 4 in equation (ii)
9(4) – 8y – 12 = 0
36 – 8y – 12 = 0
-8y + 24 = 0
-8y = -24
y = 24/8
y = 3
Therefore, required solution is x = 4, y = 3.
Example 3.
Solve the linear equations 2x + 3y = 5, x – 4y = 8 by using the cross multiplication method?
Solution:
Given linear equations are 2x + 3y = 5, x – 4y = 8
On transposing, we get
2x + 3y – 5 = 0 ——- (i)
x – 4y – 8 = 0 ——- (ii)
Multiply equation (ii) by 2, equation (i) by 1.
From equation (i), we get
2x + 3y – 5 = 0 —– (iii)
From equation (ii), we get
2(x – 4y – 8) = 0
2x – 8y – 16 = 0 —— (iv)
Subtract equation (iii) from equation (iv).
[2x – 8y – 16] – [2x + 3y – 5] = 0
2x – 8y – 16 – 2x – 3y + 5 = 0
-11y – 11 = 0
-11y = 11
y = -11/11
y = -1
Substitute y = -1 in equation (i)
2x + 3(-1) – 5 = 0
2x – 3 – 5 = 0
2x – 8 = 0
2x = 8
x = 8/2
x = 4
Therefore, the required solution is x = 4, y = -1.
Example 4.
Solve the system of linear equations 2x + 5y = 20, x + 2y = 4?
Solution:
Given simultaneous linear equations are 2x + 5y = 20, x + 2y = 4
On transposing, we get
2x + 5y – 20 = 0 —— (i)
x + 2y – 4 = 0 —— (ii)
Multiply equation (i) by 2.
2(2x + 5y – 20) = 2 x 0
4x + 10y – 40 = 0 ——- (iii)
Multiply equation (ii) by 5.
5(x + 2y – 4) = 0 x 5
5x + 10y – 20 = 0 —– (iv)
Subtract equation (iii) from equation (iv)
[5x + 10y – 20] – [4x + 10y – 40] = 0
5x + 10y – 20 – 4x – 10y + 40 = 0
x + 20 = 0
x = -20
Put x = -20 in equation (iii)
4(-20) + 10y – 40 = 0
-80 + 10y – 40 = 0
10y – 120 = 0
10y = 120
y = 120/10
y = 12
Therefore the required solution is x = -20, y = 12.