Are you searching to learn Square Root of a Perfect Square by Using the Long Division Method? Then, you can get the process to find a Square Root of a Perfect Square with the help of a Long Division Method here. We have included different types of problems, solutions, and also their explanation. Therefore, without any delay, you can begin your practice and get a grip on the complete concept.
We have given complete concepts on Square and Square Root on our website. Have a look at them and immediately start your practice.
How to find Square Root of a Perfect Square Number using Long Division Method?
Check the below steps to learn the procedure for finding the Square Root of a Number using the Long Division method.
- Group the digits in pairs using a period that starts with the digit in the units place. Each pair and the remaining digit (if any).
- Set the largest number whose square is equal to or just less than the first period. Then, you have to take this number as the divisor and also as the quotient.
- Do subtract the product of the divisor and the quotient from the first period.
- Then, write the next period to the right of the remainder and consider it as a new dividend.
- Divide the new dividend until the digit is equal to or just less than the new dividend.
- Repeat the above steps till all the periods have been taken up. Now, the quotient so obtained is the required square root of the given number.
Square Root of a Perfect Square Number using Long Division with Examples
1. Find the square root of 784 by the long-division method?
Solution:
The given number is 784.
To find the square root of a perfect square by the long division method, we have to follow the below procedure.
784 = 2 x 2 x 2 x 2 x 7 x 7
Grouping the factors into the pairs of equal factors.
(2 × 2) × (2 × 2) × (7 × 7)
Take one number from each group and multiply them to find the number whose square is 784.
2 × 2 × 7 = 28.

The square root of 784 is 28.
2. Evaluate √5329 using the long-division method?
Solution:
The given number is √5329.
To find the square root of a perfect square by the long division method, we have to follow the below procedure.
√5329 = 73 x 73
Grouping the factors into the pairs of equal factors.
(73 × 73)
Take one number from each group and multiply them to find the number whose square is 5329.
73.
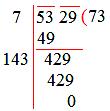
The square root of 5329 is 73.
3. Evaluate √16384?
Solution:
The given number is √16384.
To find the square root of a perfect square by the long division method, we have to follow the below procedure.
√16384 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
Grouping the factors into the pairs of equal factors.
(2 × 2) x (2 × 2) x (2 × 2) x (2 × 2) x (2 × 2) x (2 × 2) x (2 × 2)
Take one number from each group and multiply them to find the number whose square is 16384.
2 x 2 × 2 x 2 × 2 x 2 × 2 = 128.
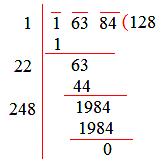
The square root of 16384 is 128.
4. Evaluate √10609?
Solution:
The given number is √10609.
To find the square root of a perfect square by the long division method, we have to follow the below procedure.
√10609 = 103 x 103
Grouping the factors into the pairs of equal factors.
(103 x 103)
Take one number from each group and multiply them to find the number whose square is 10609.
103
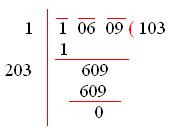
The square root of 10609 is 103.
5. Evaluate √66049?
Solution:
The given number is √66049.
To find the square root of a perfect square by the long division method, we have to follow the below procedure.
√66049 = 257 x 257
Grouping the factors into the pairs of equal factors.
(257 x 257)
Take one number from each group and multiply them to find the number whose square is 66049.
257
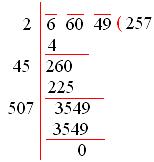
The square root of 66049 is 257.
6. Find the cost of erecting a fence around a square field whose area is 4 hectares if fencing costs $ 3.50 per meter?
Solution:
Area of the square field = (4 × 1 0000) m² = 40000 m²
Length of each side of the field = √40000 m = 200 m.
Perimeter of the field = (4 × 200) m = 800 m.
Cost of fencing = $(800 × 7/2) = $2800.
7. Find the least number that must be added to 6412 to make it a perfect square?
Solution:
Given the number is 6412,
To find the square root of a perfect square by the long division method, we have to find the factors of 6412.
6412 = (80 × 80)
Grouping the factors into the pairs of equal factors.
(80 × 80)
We observe here that (80)² < 6412 < (81)²
The required number to be added = (81)² – 6412
= 6561 – 6412
= 149
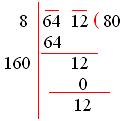
8. What least number must be subtracted from 7250 to get a perfect square? Also, find the square root of this perfect square?
Solution:
Given the number is 7250,
To find the square root of a perfect square by the long division method, we have to find the factors of 7250.
7250 = (85 × 85)
Grouping the factors into the pairs of equal factors.
(85 × 85)
So, the least number to be subtracted from 7250 is 25.
Required perfect square number = (7250 – 25) = 7225
And, √7225 = 85.
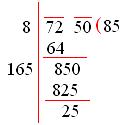
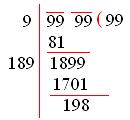
9. Find the greatest number of four digits which is a perfect square?
Solution:
The greatest number of four digits is 9999.
The square root of 9999 is
To find the square root of a perfect square by the long division method, we have to find the factors of 9999.
9999 = (99 × 99)
Grouping the factors into the pairs of equal factors.
(99 × 99)
This shows that (99)² is less than 9999 by 198.
So, the least number to be subtracted is 198.
Hence, the required number is (9999 – 198) = 9801.