Spectrum Math Grade 8 Chapters 1-6 Final Test Answer Key

Students can use the Spectrum Math Grade 8 Answer Key Chapter 1-6 Final Test as s a quick guide to resolve any of their doubts

Spectrum Math Grade 8 Chapter 1-6 Final Test Answers Key

Evaluate each expression. Simplify fractions.

Question 1.
(a) \(\sqrt{81}\) = _____
Answer:
9

Explanation:
The square root of the number is the number that multiplied by itself, equals that number.
The square root of 81 is 9.
9 x 9 = 81
So, \(\sqrt{81}\) = 9

(b) \(\sqrt[3]{343}\) = _____
Answer:
7

Explanation:
The cube of the number is the number that multiplied by itself three times.
The cube root of 343 is 7.
7 x 7 x 7 = 343
So, \(\sqrt[3]{343}\) = 7

(c) \(\sqrt{\frac{16}{25}}\) = _____
Answer:
\(\frac{4}{5}\)

Explanation:
Fractions can also have square roots as normal square roots in both numerators and denominators.
We know that,
The square root of the number is the number that multiplied by itself, equals that number.
The square root of 16 is 4.
we write as, 4 x 4 = 16
The square root of 25 is 5.
we write as, 5 x 5 = 25
So, \(\sqrt{\frac{16}{25}}\) = \(\sqrt{\frac{4}{5}}\)

Question 2.
(a) \(\sqrt[3]{\frac{27}{216}}\) = _____
Answer:
\(\frac{1}{2}\)

Explanation:
Fractions can also have cube roots as normal square roots in both numerators and denominators.
We know that,
The cube of the number is the number that multiplied by itself three times.
The cube root of 27 is 3.
3 x 3 x 3 = 27
The cube root of 216 is 6.
6 x 6 x 6 = 216
So, \(\sqrt[3]{\frac{27}{216}}\) = \(\frac{3}{6}\)
Reduce to the simplest form as, \(\frac{1}{2}\)

(b) \(\sqrt{1}\) = _____
Answer:
1

Explanation:
The square root of the number is the number that multiplied by itself, equals that number.
The square root of 1 is 1.
1 x 1 = 1
So, \(\sqrt{1}\) = 1

(c) \(\sqrt[3]{0}\) = _____
Answer:
0

Explanation:
The cube root of the number is the number that multiplied by itself three times the number.
When we calculate the ∛0, the answer is the number that multiply by itself twice will equal 0.
So, n × n × n or 0 x 0 x 0 = 0

Approximate the value to the hundredths place.

Question 3.
The value of \(\sqrt{5}\) is between ___ and _____
Answer:
2.23 and 2.24

Explanation:
When a number is not a perfect square, estimate its square root by determining which perfect square it comes between.
\(\sqrt{5}\) is between 4 and 6.
\(\sqrt{1.493}\) is 2.23 and \(\sqrt{1.496}\) is 2.24
So, \(\sqrt{5}\) is between 2.23 and 2.24.

Question 4.
Find the value of \(\sqrt{13}\) is between ____ and ____
Answer:
3.60 and 3.61

Explanation:
When a number is not a perfect square, estimate its square root by determining which perfect square it comes between.
\(\sqrt{13}\) is between 3 and 4.
\(\sqrt{1.893}\) is 3.60 and \(\sqrt{1.90}\) is 3.61
So, \(\sqrt{13}\) is between 3.60 and 3.61

Create a number line to show each set of values ¡n order from least to greatest.

Question 5.

Answer:
-3, \(\frac{7}{4}\), π, \(\sqrt{10}\)

Explanation:
Rational and irrational numbers are compared by approximating their values and placing them along a number line as shown above.
First arrange the given numbers π, \(\sqrt{10}\), -3, \(\frac{7}{4}\), from least to the greatest then arrange on number line.
-3,
\(\frac{7}{4}\) = 1.74 ,
π = 3.143,
\(\sqrt{10}\) = 3.162

Find the value of each expression.

Question 6.
a. 2² = ____
Answer:
4

Explanation:
A power of a number represents repeated multiplication of the number by itself.
In exponential numbers the base is the number that is multiplied and the exponent represents the number of times the base is used as a factor.
In 2² , 2 is the base and 2 is the exponent.
2²  means 2 is used as a factor for 2 times.
So, 2 x 2 = 4 or 2² = 4

b. 5⁸ = ____
Answer:
390,625

Explanation:
A power of a number represents repeated multiplication of the number by itself.
In exponential numbers the base is the number that is multiplied and the exponent represents the number of times the base is used as a factor.
In 5⁸ , 5 is the base and 8 is the exponent.
5⁸ means 5 is used as a factor for 8 times.
So, 5 x 5 x 5 x 5 x 5 x 5 x5 x 5 = 390,625 or 5⁸ = 390,625

c. 3⁶ = ____
Answer:
729

Explanation:
A power of a number represents repeated multiplication of the number by itself.
In exponential numbers the base is the number that is multiplied and the exponent represents the number of times the base is used as a factor.
In 3⁶ , 3 is the base and 6 is the exponent.
3⁶  means 3 is used as a factor for 6 times.
So, 3 x 3 x 3 x 3 x 3 x 3 = 729 or 3⁶ = 729

Question 7.
a. 3^-3 = ____
Answer:
\(\frac{1}{27}\)

Explanation:
When a power includes a negative exponent, express the number as 1 divided by the base and change the exponent to positive.
3³ = 3 x 3 x 3 = 27
So, 3^-3 = \(\frac{1}{27}\)

b. 10^-4 = ____
Answer:
\(\frac{1}{10,000}\)

Explanation:
When a power includes a negative exponent, express the number as 1 divided by the base and change the exponent to positive.
10⁴ = 10 x 10 x 10 x 10 = 10,000
So, 10^-4 = \(\frac{1}{10,000}\)

c. 2^-6 = ____
Answer:
\(\frac{1}{64}\)

Explanation:
When a power includes a negative exponent, express the number as 1 divided by the base and change the exponent to positive.
2⁶ = 2 x 2 x 2 x 2 x 2 x 2  = 64
So, 2^-6 = \(\frac{1}{64}\)

Write each number in scientific notation or standard form.

Question 8.
a. 103.6 = _________
Answer:
1.036 x 10²

Explanation:
Scientific notation is the most often used as a concise way of writing very large and small numbers. It is written  as a number between 1 and 10 multiplied by a power of 10.
103.6 is written as 1.036 x 10²
So, 1.036 x 10 x 10 = 103.6
Hence, 1.036 = 1.036 x 10²

b. 4.2 × 10^-1 = _________
Answer:
0.42

Explanation:
Scientific notation is the most often used as a concise way of writing very large and small numbers. It is written  as a number between 1 and 10 multiplied by a power of 10.
4.2 × 10^-1 is written as 0.42

c. 0.082 = ________
Answer:
8.2 x 10^-2

Explanation:
Scientific notation is the most often used as a concise way of writing very large and small numbers. It is written  as a number between 1 and 10 multiplied by a power of 10.
0.082 is written as 8.2 x 10^-2

Question 9.
a. 5.86 × 10² = _________
Answer:
586

Explanation:
Scientific notation is the most often used as a concise way of writing very large and small numbers. It is written  as a number between 1 and 10 multiplied by a power of 10.
5.86 x 10² = 586
5.86 x 10 x 10 = 586

b. 19,300 = _________
Answer:
1.93 x 10⁴

Explanation:
Scientific notation is the most often used as a concise way of writing very large and small numbers. It is written  as a number between 1 and 10 multiplied by a power of 10.
19,300 is written as 1.93 x 10⁴
So, 1.93 x 10 x 10 x 10 x 10 = 19,300
Hence, 19,300 = 1.93 x 10⁴

c. 7.6 × 10^-2 = ____
Answer:
0.076

Explanation:
Scientific notation is the most often used as a concise way of writing very large and small numbers. It is written  as a number between 1 and 10 multiplied by a power of 10.
7.6 × 10^-2 is written as 0.076.

Question 10.
a. 3,604 = _________
Answer:
3.604 x 10³

Explanation:
Scientific notation is the most often used as a concise way of writing very large and small numbers. It is written  as a number between 1 and 10 multiplied by a power of 10.
3,604 is written as 3.604 x 10³
So, 3.604 x 10 x 10 x 10 = 3,604
Hence, 1.036 = 1.036 x 10²

b. 5 × 10^-3 = _________
Answer:
0.005

Explanation:
Scientific notation is the most often used as a concise way of writing very large and small numbers. It is written  as a number between 1 and 10 multiplied by a power of 10.
5 × 10^-3 is written as 0.005

c. 0.0063 = _____
Answer:
6.3 x 10^-3

Explanation:
Scientific notation is the most often used as a concise way of writing very large and small numbers. It is written  as a number between 1 and 10 multiplied by a power of 10.
0.0063 is written as 6.3 x 10^-3
So, 6.3 x 10 x 10 x 10 = 0.0063
Hence, 0.0063 = 6.3 x 10^-3

Rewrite the multiplication or division

Question 11.
a. 3⁴ × 3³ = _________
Answer:
3⁷

Explanation:
Given,
3⁴ × 3³
To multiply the powers with the same base, combine the bases and add the exponents and then simplify.
3⁴ × 3³ = 3⁴⁺³ = 3⁷

b. 2^-6 × 2^-2 = _________
Answer:
2^-8

Explanation:
Given,
2^-6 × 2^-2
To multiply the powers with the same base, combine the bases and add the exponents and then simplify.
2^-6 × 2^-2 = 2^-6-2 = 2^-8

c. 5^-3 ÷ 5^-6 = _________
Answer:
5³

Explanation:
Given,
5^-3 ÷ 5^-6
To divide the powers with the same base, combine the bases and subtract the exponents and then simplify.
5^-3 ÷ 5^-6 = 5^{-3 + 6} = 5³

Question 12.
a. 4¹⁰ ÷ 4^-4 = _________
Answer:
4¹⁴

Explanation:
Given,
4¹⁰ ÷ 4^-4
To divide the powers with the same base, combine the bases and subtract the exponents and then simplify.
4¹⁰ ÷ 4^-4  = 4¹⁰⁺⁴ = 4¹⁴

b. 8² × 8^-3 = _________
Answer:
8^-1

Explanation:
Given,
8² × 8^-3
To multiply the powers with the same base, combine the bases and add the exponents and then simplify.
8² × 8^-3 = 8^2-3 = 2^-1

c. 10^-6 ÷ 10⁴ = _________
Answer:
10^-10

Explanation:
Given,
10^-6 ÷ 10⁴
To divide the powers with the same base, combine the bases and subtract the exponents and then simplify.
10^-6 ÷ 10⁴ = 10^-6-4 = 10^-10

Question 13.
a. 6^-3 × 6^-3 = _________
Answer:
6^-6

Explanation:
Given,
6^-3 × 6^-3
To multiply the powers with the same base, combine the bases and add the exponents and then simplify.
6^-3 × 6^-3 = 6^-3-3 = 6^-6

b. 11^-7 ÷ 11³ = _________
Answer:
11^-10

Explanation:
Given,
11^-7 ÷ 11³
To divide the powers with the same base, combine the bases and subtract the exponents and then simplify.
11^-7 ÷ 11³ = 11^-7-3 = 11^-10

c. 7^-3 ÷ 7² = _________
Answer:
7^-1

Explanation:
Given,
7^-3 ÷ 7²
To divide the powers with the same base, combine the bases and subtract the exponents and then simplify.
7^-3 ÷ 7² = 7^-3-2 = 10^-1

Determine if the slope, or rate of change, is constant or variable. Show your work.

Question 14.
Mike is on his way to school. The table below shows how far he has traveled and how long he has been traveling.

Answer:
Variable.

Explanation:
The rate of change in the time travelled divided by the rate of change in the distance travelled.
m = \(\frac{The time travelled}{The distance travelled}\)
m = \(\frac{12 – 10}{0.75 – 0.5}\)
m = \(\frac{2}{0.25}\)
m = 80 miles
m = \(\frac{The time travelled}{The distance travelled}\)
m = \(\frac{25 – 15}{1 – 0.75}\)
m = \(\frac{10}{0.25}\)
m = 40 miles

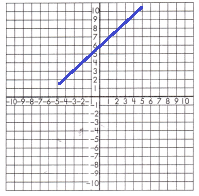
Use the slope-intercept form of equations to draw lines on the grids below.

Question 15.
a.

Answer:

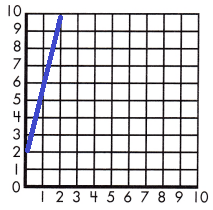
Explanation:
y = 4x + 2
for x = 0
y = 4(0) + 2 = 2
for x = 1
y = 4(1) + 2 = 6
for x = 2
y = 4(2) + 2 = 10

b.

Answer:

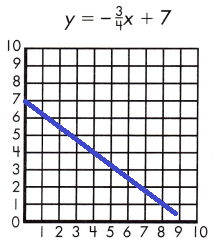
Explanation:
y = \(\frac{-3}{4}\) x + 7
for x = 0
y = \(\frac{-3}{4}\) 0 + 7 = 7
for x = 4
y = \(\frac{-3}{4}\) 4 + 7 = 4
for x = 8
y = \(\frac{-3}{4}\) 8 + 7 = 1

Find the value of the variable in each equation.

Question 16.
a. 3n + 2 = 23 ____
Answer:
7

Explanation:
Variable equations can be solved by isolating the variable on one side of the equation by performing the inverse operations.
Given,
3n + 2 = 23
3n = 23 – 2
3n = 21
n = 21 ÷ 3
n = 7

b. \(\frac{14}{m}\) + 6 = 8 _____
Answer:
7

Explanation:
Variable equations can be solved by isolating the variable on one side of the equation by performing the inverse operations.
Given,
\(\frac{14}{m}\) + 6 = 8
\(\frac{14}{m}\) = 8 – 6
\(\frac{14}{m}\) = 2
m = 14 ÷ 2
m = 7

c. 3t = 48 ____
Answer:
16

Explanation:
Variable equations can be solved by isolating the variable on one side of the equation by performing the inverse operations.
Given,
3t = 48
t = 48 ÷ 3
t = 16

Question 17.
a. p ÷ 5 = 21 ______
Answer:
105

Explanation:
Variable equations can be solved by isolating the variable on one side of the equation by performing the inverse operations.
Given,
p ÷ 5 = 21
p = 21 x 5
p = 105

b. x + 54 = 72  ____
Answer:
18

Explanation:
Variable equations can be solved by isolating the variable on one side of the equation by performing the inverse operations.
Given,
x + 54 = 72
x = 72 – 54
x = 18

c. 49 – a = 36 ______
Answer:
13

Explanation:
Variable equations can be solved by isolating the variable on one side of the equation by performing the inverse operations.
Given,
49 – a = 36
49 – 36 = a
13 = a

Question 18.
a. 15b – 2 = 58 ____
Answer:
4

Explanation:
Variable equations can be solved by isolating the variable on one side of the equation by performing the inverse operations.
Given,
15b – 2 = 58
15b = 58 + 2
15b = 60
b = 60 ÷ 15
b = 4

b. \(\frac{n}{12}\) + 4 = 9 ____
Answer:
60

Explanation:
Variable equations can be solved by isolating the variable on one side of the equation by performing the inverse operations.
Given,
\(\frac{n}{12}\) + 4 = 9
\(\frac{n}{12}\) = 9 – 4
\(\frac{n}{12}\) = 5
n = 12 x 5
n = 60

c. 108 ÷ m = 6 ____
Answer:
18

Explanation:
Variable equations can be solved by isolating the variable on one side of the equation by performing the inverse operations.
Given,
108 ÷ m = 6
m = 108 ÷ 6
m = 18

Use substitution or elimination to solve each system of equations.

Question 19.
a.
y = –\(\frac{1}{2} x\) + 18
y = -x + 20
x = ___, y = ____
Answer:
x = 4, y = 16

Explanation:
Substitute the value of y in the given equation,
y = -x + 20
–\(\frac{1}{2} x\) + 18 = -x + 20
–\(\frac{1}{2} x\) = -x + 20 – 18
–\(\frac{1}{2} x\) = -x + 2
x = 2 + 2
x = 4
Substitute the value of y in the given equation,
y = -x + 20
y = -4 + 20
y = 16
So, the values of x = 4 and y = 16

b.
y = x – 11
4x + \(\frac{4}{5} y\) = 68
x = ___, y = ____
Answer:
x = 16, y = 5

Explanation:
Substitute the value of y in the given equation,
y = x – 11
4x + \(\frac{4}{5} y\) = 68
20x + 4y = 340
20x + 4(x-11) = 340
20x + 4x – 44 = 340
24x = 384
x = 16
y = x – 11
y = 16 – 11
y = 5
c.
-8x + 2y = -48
6x – 2y = 28
x = _____, y = ______
Answer:
x = 10, y = 16

Explanation:
-8x + 2y = -48
6x – 2y = 28
divide the equation by 2 on both side as shown below
6x – 2y = 28
3x – y = 14
y = 3x – 14
-8x + 2y = -48
-8x + 2(3x – 14) = -48
-8x + 6x – 28 = -48
-2x = -20
x = 10
substitute the value of x in below equation for value y
y = 3x – 14
y = 3(10) – 14
y = 30 – 14
y = 16

Use slope-intercept form to graph each system of equations and solve the system.

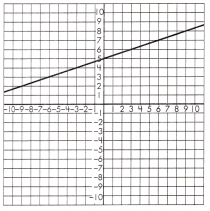
Question 20.
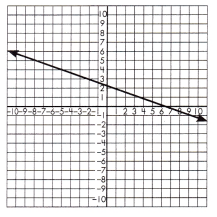
a. y = -2x – 3
y = 2x
x = ____;
y = _____

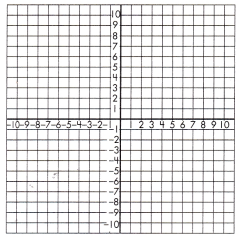
Answer:
x = –\(\frac{3}{4}\);
y = -1\(\frac{1}{2}\)

b.
y = \(\frac{3}{4}\)x – 3
y = –\(\frac{1}{2}\)x + 2
x = ____;
y = _____

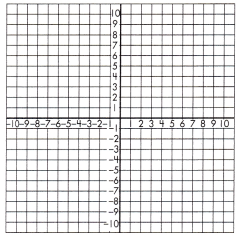
Answer:
x = 4; y = 0

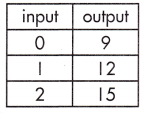
Decide if each table represents a function by stating yes or no.

Question 21.
a.

______
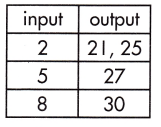
Answer:
No,

Explanation:
This table does not represent a function because one of the input variables has more than one output variable.
In out put two variables are there for single input.

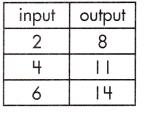
b.

______
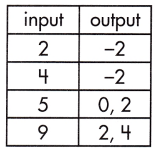
Answer:
No,

Explanation:
This table does not represent a function because one of the input variables has more than one output variable.
In out put two variables are there for single input.

c.

______
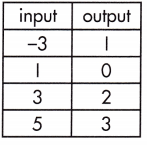
Answer:
Yes,

Explanation:
A function is a relationship between two variables which results in only one output value for each input value.
out put = input – x

Find the rate of change for each function below.

Question 22.
a.

Answer:
2

Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.

\(\frac{8 – 0}{3-(-1)}\)
= \(\frac{8}{4}\) = 2

b.

Answer:
2

Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.

\(\frac{12.5 -(-3.5)}{6 -(-2)}\)
= \(\frac{16}{8}\) = 2

c.

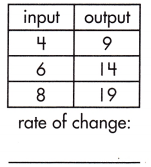
Answer:
\(\frac{5}{2}\)

Explanation:
The rate of change that exists in a function can be calculated by finding the ratio of the amount of change in the output variable to the amount of change in the input variable.

\(\frac{19 – 9}{8 – 4}\)
= \(\frac{10}{4}\) = \(\frac{5}{2}\)

Find the initial value For each problem.

Question 23.
Joan is filling her bathtub. After 2 minutes of running the water, there are 10 gallons of water ¡n the bathtub. How much water will be ¡n the tub after 5 minutes?
Initial Value:
_______
Answer:
Initial value: 0
After 5 min there will be 25 gallons of water in the tub.

Explanation:
Given that,
Joan is filling her bathtub.
After 2 minutes of running the water, there are 10 gallons of water in the bathtub.
Total water will be in the tub after 5 minutes,
2 min = 10 gal
5 min = (10 x 5) ÷ 2
So, 50 ÷ 2 = 25 gal

Question 24.
Paul lives 7 miles from the park. After 5 minutes of bicycling, he still has 6 miles left before he gets to the park. How far
will he have traveled after 20 minutes of bicycling?
Initial Value:
_______
Answer:
Initial value: 7
Paul travelled 4 miles for 20 minutes.

Explanation:
Given that,
Paul lives 7 miles from the park.
So, initial value is 7.
After 5 minutes of bicycling, he still has 6 miles left before he gets to the park.
Paul travelled after 20 minutes of bicycling,
5 min = 1 mile
20 min = 20 ÷ 5 = 4 miles.

Complete each function table for the given function.

Question 25.
a.

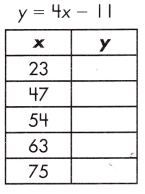
Answer:

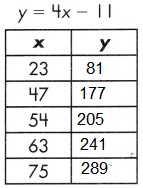
Explanation:
A function is a relationship between two variables which results in only one output value for each input value.
y = 4x – 11
y = (4 x 23) – 11 = 92 – 11 = 81
y = (4 x 47) – 11 = 188 – 11 = 177
y = (4 x 54) – 11 = 216 – 11 = 205
y = (4 x 63) – 11 = 252 – 11 = 241
y = (4 x 75) – 11 = 300 – 11 = 289

b.

Answer:

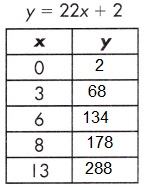
Explanation:
A function is a relationship between two variables which results in only one output value for each input value.
y = 22x + 2
y = (22 x 0) + 2 = 0 + 2 = 2
y = (22 x 3) + 2 = 66 + 2 = 68
y = (22 x 6) + 2 = 132 + 2 = 134
y = (22 x 8) + 2 = 176 + 2 = 178
y = (22 x 13) + 2 = 286 + 2 = 288

c.

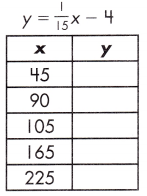
Answer:

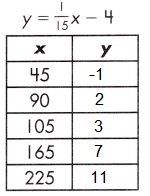
Explanation:
A function is a relationship between two variables which results in only one output value for each input value.
y = \(\frac{1}{15}\)× – 4
y = \(\frac{1}{15}\) x 45 – 4 = \(\frac{45}{15}\) – 4 = 3 – 4 = -1
y = \(\frac{1}{15}\) x 90 – 4 = \(\frac{90}{15}\) – 4 = 6 – 4 = 2
y = \(\frac{1}{15}\) x 105 – 4 = \(\frac{105}{15}\) – 4 = 7 – 4 = 3
y = \(\frac{1}{15}\) x 165 – 4 = \(\frac{165}{15}\) – 4 = 11 – 4 = 7
y = \(\frac{1}{15}\) x 225 – 4 = \(\frac{225}{15}\) – 4 = 15- 4 = 11

Construct a function model, or equation, for each situation in the form of y = mx + b.

Question 26.
a.

Function model:
y = _____
Answer:
y = 3x + 8

Explanation:
The rate of change (or slope), and plugging known values into the equation,
y = mx + b.
Step 1: Calculate the rate of change.
\(\frac{15-9}{2-0}\)
= \(\frac{6}{2}\) = 3
Step 2: Substitute known values of x and y into the slope-intercept form of the equation.
y = mx + b
(9) = 3 (0) + b
Step 3: Solve to find the initial value of the output variable (b).
(9) = 3 (0) + b
9 = 0 + b
b = 9
Step 4: Write the equation using the found values of m and b.
y = 3x + 9

b.

Function model:
y = _____
Answer:
y = \(\frac{3}{2}\)x + 5

Explanation:
The rate of change (or slope), and plugging known values into the equation,
y = mx + b.
Step 1: Calculate the rate of change.
\(\frac{14-8}{6-2}\)
= \(\frac{6}{4}\)
= \(\frac{3}{2}\)
Step 2: Substitute known values of x and y into the slope-intercept form of the equation.
y = mx + b
(8) = \(\frac{3}{2}\) (2) + b
Step 3: Solve to find the initial value of the output variable (b).
b = 8 – 3
b = 5
Step 4: Write the equation using the found values of m and b.
y = mx + b
y = \(\frac{3}{2}\)x + 5
c.

Function model:
y = _____
Answer:
y = \(\frac{1}{3}\)x + 5

Explanation:
Step 1: Find and name two points on (3, 6) and (-3, 4) the line.
Step 2: Calculate the rate of change.
\(\frac{4 – 6}{-3- 3}\)
= –\(\frac{2}{6}\)
= –\(\frac{1}{3}\)
Step 3: Use the found points and calculated slope to find the initial value of the output if it cannot be determined based on the graph.
Based on the graph, the initial value of the output variable for a value (x, y)
Step 4: Write the formula for all values of x and y using the equation.
y = mx + b
y = –\(\frac{1}{3}\) + b
for x = 0
y = 5
5 = –\(\frac{1}{3}\) 0 + b
b = 5
y = mx + b
y = –\(\frac{1}{3}\)x + 5

Compare the rate of change for the equations and tables shown below and decide which has a greater rate of change by writing equation or table.

Question 27.
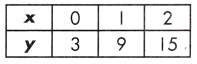
a. y = 2x + 4 or

_______
Answer:
Table.

Explanation:
Rate of change for table = \(\frac{15-3}{2-0}\) = \(\frac{12}{2}\) = 6
Rate of change for equation,
y = 2x + 4
y = 4
Rate of change for table,
y = mx + b
3 = (6 x 0) + b
b = 3
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the table is larger than the rate of change shown by the equation.

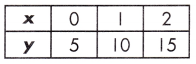
b. y = 6x + 7 or

Answer:
Equation.

Explanation:
Rate of change for table = \(\frac{15-5}{2-0}\) = \(\frac{10}{2}\) = 5
Rate of change for equation,
y = 5x + b
Rate of change for table,
y = mx + b
10 = (5 x 1) + b
b = 5
y = 5x + 5
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the equation is larger than the rate of change shown by the table..

c.
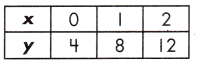
y = -7x + 4 or

Answer:
Equation.

Explanation:
Rate of change for table = \(\frac{12-4}{2-0}\) = \(\frac{8}{2}\) = 4
Rate of change for equation,
y = -7x + 4
m = -7 in equation
Rate of change for table,
y = mx + b
4 = (4 x 0) + b
b = 4
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the equation is greater then the rate of change shown by the table..

Sketch each linear function.

Question 28.
a.
y = x + 6

Answer:

Explanation:
for x= 0
y = x + 6
y = 0 + 6
y = 6
for x= 1
y = 1 + 6
y = 1 + 6
y = 7
for x= 2
y = x + 6
y = 2 + 6
y = 8
Mark the point where the line will cross the y-axis (b = 6).
Draw a line that goes directly through the points found.

b. y = 3x + 1

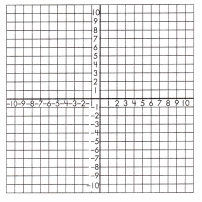
Answer:

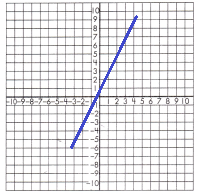
Explanation:
for x= 0
y = 3x + 1
y = 3(0) + 1
y = 1
for x= 1
y = 3(1) + 1
y = 3 + 1
y = 4
for x= 2
y = 3(2) + 1
y = 6 + 1
y = 7
Mark the point where the line will cross the y-axis (b = 1).
Draw a line that goes directly through the points found.

Complete the function table for each function. Then, graph the function.

Question 29.
a.

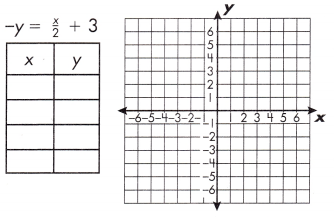
Answer:

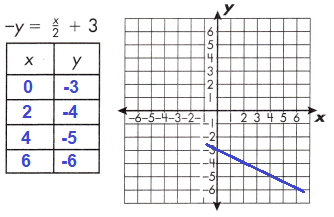
Explanation:
-y = \(\frac{x}{2}\) + 3
for x = 0
-y = \(\frac{0}{2}\) + 3
-y = 3
y = -3
for x = 2
-y = \(\frac{2}{2}\) + 3
-y =1 + 3
y = -4
for x = 4
-y = \(\frac{4}{2}\) + 3
-y = 2 + 3
y = -5
for x = 6
-y = \(\frac{6}{2}\) + 3
-y = 3 + 3
y = -6

b.

Answer:

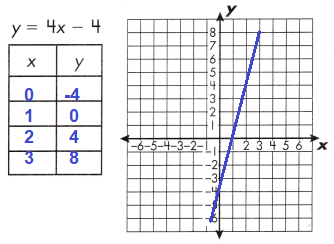
Explanation:
for x= 0
y = 4x – 4
y = 0 – 4
y = -4
for x= 1
y = 4(1) – 4
y = 4 – 4
y = 0
for x= 2
y = 4x – 4
y = 8 – 4
y = 4
for x= 3
y = 4x – 4
y = 12 – 4
y = 8

State if the figures below represent a rotation, reflection, or translation.

Question 30.
a.

Answer:
Rotation.

Explanation:
Rotation:
Rotation is a turn of a figure, which can be rotated any number of degrees.

b.

_______
Answer:
Reflection.

Explanation:
Reflection is a flip of a figure, which can be flipped up, down or to the side.

c.

________
Answer:
Translation.

Explanation:
Translation is known as slide of a given figure.
The figure can be slide up, down or sideways, but the size, shape and orientation of the figure remains same.

Write the steps each figure must go through to be transformed from figure 1 to figure 2.

Question 31.

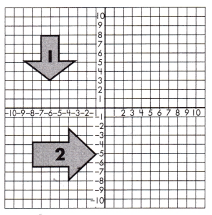
Step 1 : ______________
Step 2 :______________
Step 3 :______________
Answer:
Step 1 : rotate 90 degrees.
Step 2 : translate on x-axis.
Step 3 : dilate by 2

Explanation:
Rotate the figure of 90 degrees clock wise, each point of the given figure has to be changed from (x, y) to (y, -x) and the graph is rotated figure.
Horizontally translating a graph is equivalent to shifting the base graph left or right in the direction of the x-axis.
A graph is translated k units horizontally by moving each point on the graph k units horizontally., g(x) = f (x – k).
To dilate the figure by a factor of 2, multiply the x and y-value of each point by 2.
Plot all the new points to find the new image. To dilate the figure by a factor of 2,
multiply the x and y-value of each point by 2.

Question 32.

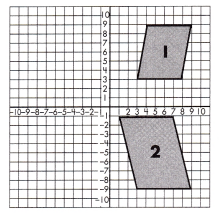
Step 1 : ______________
Step 2 :______________
Step 3 :______________
Answer:
Step 1 : reflect on x-axis.
Step 2 : translate on x-axis.
Step 3 : dilate by 2

Explanation:
A point is reflected about x – axis, its image is just opposite to itself on the other side of x – axis due to which its x – coordinate remains same but y – coordinate changes.
Horizontally translating a graph is equivalent to shifting the base graph left or right in the direction of the x-axis.
A graph is translated k units horizontally by moving each point on the graph k units horizontally, g(x) = f (x – k).
To dilate the figure by a factor of 2, multiply the x and y-value of each point by 2.
Plot all the new points to find the new image.
To dilate the figure by a factor of 2, multiply the x and y-value of each point by 2.

Use similar right triangles to prove that each line has a constant slope.

Question 32.

Triangle 1 Legs:
_____ & _____
Triangle 2 Legs:
_____ & _____
Proportionality Test:
___________ = ______________
Answer:
Triangle 1 Legs: 2 & 1
Triangle 2 Legs: 4 & 2
Proportionality Test:
2 x 2 = 4
1 x 4 = 4

Question 33.

Triangle 1 Legs:
_____ & _____
Triangle 2 Legs:
_____ & _____
Proportionality Test:
___________ = ______________
Answer:
Triangle 1 Legs: 1 & 3
Triangle 2 Legs: 2 & 6
Proportionality Test:
1 x 6 = 6
2 x 3 = 6

Answer each question using letters to name each line and numbers to name each angle.

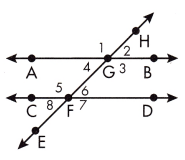
Question 33.
Which 2 lines are parallel?
Answer:
AB ∥ CD

Explanation:
Parallel lines are lines in a plane that are always with the same distance and never intersect.
So, AB ∥ CD as shown in the given figure.

Question 34.
What is the name of the transversal?
Answer:
EH

Explanation:
A transversal line is a line that intersects two or more lines at distinct points.
So, EH is a transversal line in the given figure.

Question 35.
Which angles are obtuse?
Answer:
∠1, ∠3, ∠5, ∠7

Explanation:
An obtuse angle is an angle which is greater than 90° and less than 180°.
Angle  between a right angle and a straight angle is also known as obtuse angle.

Question 36.
Which pairs of angles are alternate exterior angles?
Answer:
∠1 and ∠7; ∠2 and ∠8

Explanation:
Exterior angle is defined as the angle formed between a side of triangle and an adjacent side extending outward as shown in the given figure.

Question 37.
Which pairs of angles are alternate interior angles?
Answer:
∠4 and ∠6; ∠5 and ∠3

Explanation:
Interior angles refer to all those angles that are inside a shape.
Interior angle is defined as the angle formed between two adjacent sides of a triangle as shown in the given figure.

Use the Pythagorean Theorem to find the unknown lengths.

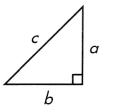
Question 38.
If a = 8 and b = 9, c = \(\sqrt{}\) or bout ___________
Answer:
\(\sqrt{145}\) or 12.04

Explanation:
According to Pythagorean Theorem,
c²= a²+ b²
a = 8, b = 9
a²+=8 x 8 = 64
b² = 9 x 9 = 81
c = \(\sqrt{64 + 81}\)
c = \(\sqrt{145}\)
c = 12.04

Question 39.
If a = 15 and b = 10, c = \(\sqrt{}\) or about _________
Answer:
\(\sqrt{325}\) or 18.03

Explanation:
According to Pythagorean Theorem,
c²= a²+ b²
a = 15, b = 10
a²+=15 x 15 = 225
b² = 10 x 10 = 100
c = \(\sqrt{225 + 100}\)
c = \(\sqrt{325}\)
c = 18.03

Find the volume of each figure.

Question 40.

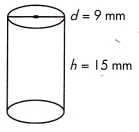
V = ____________ mm³
Answer:
V = 953.78 or 954 mm³

Explanation:
Volume of a cylinder = πr²h cubic units.
Given,
diameter = 9mm
radius = d/2
r = 9/2 = 4.5 mm
So, r² = 4.5 x 4.5 = 20.25mm
height = 15 mm
π = 22/ 7 or = 3.142
Substitute all the values in the formula.
V = 3.1428 x 20.25 x 15
V = 6682.5/7
V = 953.78 or 954 mm³

Question 41.

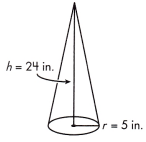
V = ____________ in.³
Answer:
V = 628 in³

Explanation:
volume of a cone = 1/3(πr²h) cubic units.
Given,
radius = 5 in, height = 24 in.
V = 1/3 (3.1428 x 5 x 5 x 24)
V = 1/3(1885.68)
V = 628.56 or 628 in³

Question 42.

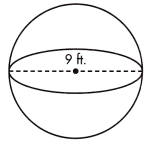
V = ____________ ft.³
Answer:
V = 381.51 ft³

Explanation:
Volume of sphere = 4/3(πr³)
Given,
Diameter = 9 ft
radius = d/2
r = 9/2 = 4.5 ft
r³ = 91.125 ft
V = 4/3 (3.1428 x 91.125)
V = 1145.55 ÷ 3
V = 381.51 ft³

Answer the questions by interpreting data from the graph.

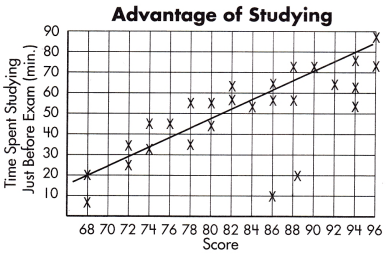
Question 41.
What two sets of data are being compared by this scatter plot?
Answer:
Time spent studying and Test scores.

Explanation:
A scatter plot shows the relationship between two sets of data.
It is made up of points, Test scores and Time spent on studying.
So, the two sets of data are being compared by this scatter plot are Time spent studying and Test scores.

Question 42.
Is the correlation positive or negative?
Answer:
Positive.

Explanation:
The above scatter plot shows the relationship between the Time spent studying and Test scores.
We observe a positive relationship as the time spent on studying increases the test scores also increases.

Question 43.
What is a possible explanation for the outliers?
Answer:
Students studied earlier.

Explanation:
The above scatter plot shows the relationship between the Time spent studying and Test scores.
Create a trend line by using a straight edge to draw a line across the points on a scatter plot.
To have the same number of points above and below the trend line while ignoring outliers.
Based on the outliers the students earlier got good score in test.

Answer the questions by interpreting data from the graph.

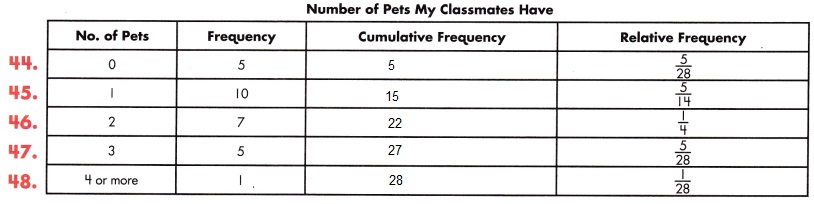
Question 49.
How many students were polled?
Answer:
28

Explanation:
The above chart shows that the number of pets my classmates have.
The total number of pets that my classmates have 5 + 10 + 7 + 5 +1 = 28

Question 50.
What was the most frequent response? ____________ How many gave that response? _____________
Answer:
1; 10

Explanation:
The above chart shows that the number of pets my classmates have, with the most frequent pet is only one for ten classmates.