Spectrum Math Grade 8 Chapter 5 Pretest Answer Key

Students can use the Spectrum Math Grade 8 Answer Key Chapter 5 Pretest as a quick guide to resolve any of their doubts.

Spectrum Math Grade 8 Chapter 5 Pretest Answers Key

Check What You Know

Geometry

Question 1.
What are the coordinates of the preimage?
A(_______), B(_______), C(_______)
Answer: (-4, -1), (-1, -1), (-1, 5)
The coordinates of the preimage are (-4, -1), (-1, -1), (-1, 5)

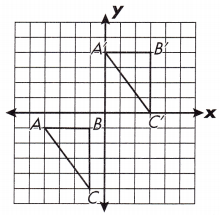
Question 2.
What are the coordinates of the image?
A’( _____________ ), B’( _____________ ), C’( _____________ )
Answer: (0, 4), (3, 4), (3, 0)
The coordinates of the image are (0, 4), (3, 4), (3, 0)

Question 3.
What transformation was performed on the figure? _______
Answer: translation
The transformation of the figure that was performed was translation.

Question 4.
a.

_____________
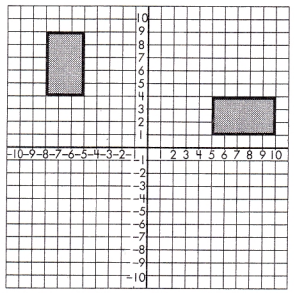
Answer: congruent
If there exists a sequence of translations, reflections, rotations, and/or dilations that will transform one figure into the other, the two figures are either similar or congruent. Similar figures are the same shape but not the same size while congruent shapes are both the same shape and the same size.

b.

_____________
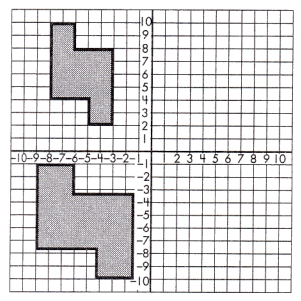
Answer: neither
If there exists a sequence of translations, reflections, rotations, and/or dilations that will transform one figure into the other, the two figures are either similar or congruent. Similar figures are the same shape but not the same size while congruent shapes are both the same shape and the same size.

c.

_____________
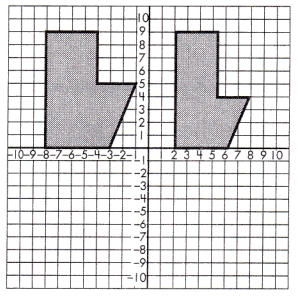
Answer: neither
If there exists a sequence of translations, reflections, rotations, and/or dilations that will transform one figure into the other, the two figures are either similar or congruent. Similar figures are the same shape but not the same size while congruent shapes are both the same shape and the same size.

Draw similar right triangles to show that each line has a constant slope.

Question 5.
a.

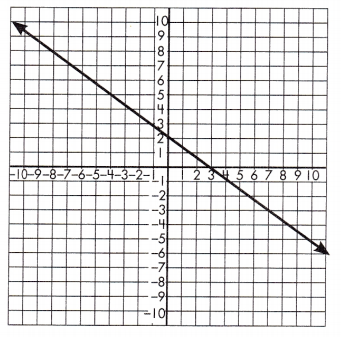
Triangle 1 Legs: ____ & ______
Triangle 2 Legs: ____ & ______
Answer:

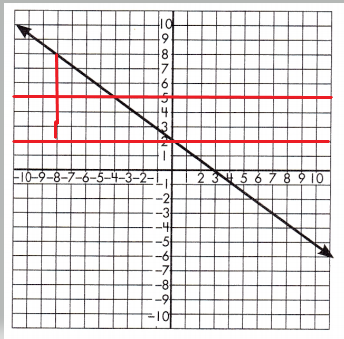
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
4 & 3
Triangle 2 Legs:
8 & 6
Proportionality Test:
\(\frac{4}{3}\) = \(\frac{8}{6}\)
4 x 6 = 24 and 8 x  3 = 24
These leg lengths are proportional, so the line has a constant slope.

b.

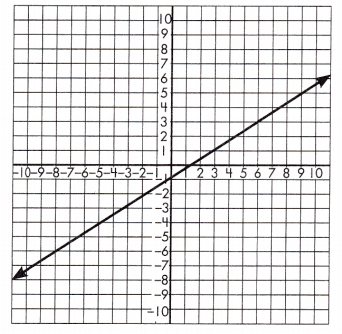
Triangle 1 Legs: ____ & ______
Triangle 2 Legs: ____ & ______
Answer:

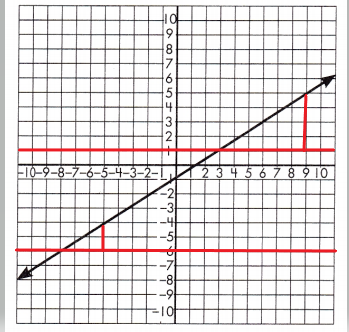
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
3 & 2
Triangle 2 Legs:
6 & 4
Proportionality Test:
\(\frac{3}{2}\) = \(\frac{6}{4}\)
3 x 4 = 12 and 6 x  2 = 12
These leg lengths are proportional, so the line has a constant slope.

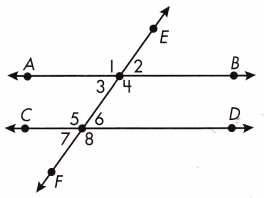
Answer each question using letters to name each line and numbers to name each angle.

Question 6.
What is the name of the transversal? ______
Answer: \(\overleftrightarrow{EF}\)
The name of the transversal is \(\overleftrightarrow{EF}\)

Question 7.
Which angles are acute? ______
Answer: ∠2, ∠3, ∠6, ∠7
An acute angle measure less than 90 degrees.

Question 8.
Which angles are obtuse? _________________
Answer: ∠1, ∠4, ∠5, ∠8
An acute angle measure greater than 90 degrees.

Question 9.
Which pairs of angles are vertical angles? ______
Answer: ∠1/∠4, ∠2/∠3, ∠5/∠8, ∠6/∠7

Question 10.
Which pairs of angles are alternate exterior angles?
_____________
Answer: ∠1/∠8, ∠2/∠7
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.

Question 11.
Which pairs of angles are alternate interior angles? ______
Answer: ∠3/∠6, ∠4/∠5
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.

Find the volume of each figure. Use 3.14 for π. Round answers to the nearest hundredth.

Question 12.
a.

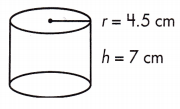
V = _____ cm³
Answer: 445.1  cm³
Volume is the amount of space a three-dimensional figure occupies. The volume of a cylinder by multiplying the area of the base by the height (Bh). The area of the base is the area of the circle, πr², so volume can be found using the formula: V = πr²h
The volume is expressed in cubic units, or units³.
The given values are r = 4.5cm  and h = 7 cm.
Use 3.14 for π.
So, V = πr²h V = π(4.5² × 7) V = 445.1 cm³

b.

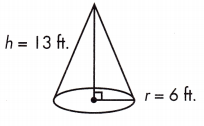
V = _____ ft³
Answer: 489.84 ft³
Volume is the amount of space a three-dimensional figure occupies. The volume of a cone is calculated as \(\frac{1}{3}\)base × height.
This is because a cone occupies \(\frac{1}{3}\) of the volume of a cylinder of the same height. Base is the area of the circle, πr².
radius = 6 ft
height = 13 ft
V = \(\frac{1}{3}\)π6² 13  = 489.84 ft³

c.

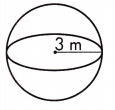
V = _____ m³
Answer: 113.04 m³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
r = 3 m
V = \(\frac{4}{3}\)πr(3)³ = 113.04 m³

Use the Pythagorean Theorem to find the unknown lengths.

Question 13.
If a = 8 and b = 15, c = or _______
Answer:  \(\sqrt{289}\) or 17
\(\sqrt{149}\) or 12.2
The Pythagorean Theorem:
If a triangle is a right triangle, then a² + b² = c².
a = 8, b = 15 , c =?
a² + b² = c²
a² + b² = 8² + 15²  = 64 + 225 = 289
c² = a² + b²  = 289
\(\sqrt{c}\) = \(\sqrt{289}\) = 17

 

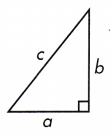
Question 14.
If b = 7 and c = 13, a = or about _____
Answer:  \(\sqrt{120}\) or 11
The Pythagorean Theorem:
If a triangle is a right triangle, then a² + b² = c².
a = ?, b = 7, c =13
a² + b² = c²
c² –  b² = 13² – 7²  = 120
b² = c² – a² = 120
\(\sqrt{b}\) = \(\sqrt{120}\) = 11

Question 15.
if a = 9 and c = 20, b = = =_______ or about _____
Answer: \(\sqrt{319}\) or 18
The Pythagorean Theorem:
If a triangle is a right triangle, then a² + b² = c².
a = 9, b = ? , c =20
a² + b² = c²
c² –  a² = 20² – 9²  = 319
b² = c² – a² = 319
\(\sqrt{b}\) = \(\sqrt{319}\) = 18