Students can use the Spectrum Math Grade 8 Answer Key Chapter 5 Lesson 5.6 Transversals and Calculating Angles as a quick guide to resolve any of their doubts.
Spectrum Math Grade 8 Chapter 5 Lesson 5.6 Transversals and Calculating Angles Answers Key
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
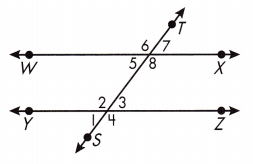
In the figure, \(\overleftrightarrow{S T}\) is a transversal. \(\overleftrightarrow{W X}\) and \(\overleftrightarrow{Y Z}\) are parallel.
The alternate interior angles are ∠2 and ∠8, and ∠3 and ∠5.
The alternate exterior angles are ∠4 and ∠6, and ∠1 and ∠7.
The corresponding angles are ∠1 and ∠5, ∠2 and ∠6, ∠3 and ∠7, and ∠4 and ∠8.
Use the figure to the right. Name the transversal that forms each pair of angles. Write whether the angles are alternate interior, alternate exterior, or corresponding.
Question 1.
∠1 and ∠9 ______ __________
Answer: \(\overleftrightarrow{RS}\) , Corresponding
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 2.
∠5 and ∠4 ______ _____
Answer: \(\overleftrightarrow{AB}\), alternate interior
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 3.
∠11 and ∠3 _____ ______
Answer: \(\overleftrightarrow{RS}\), corresponding
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
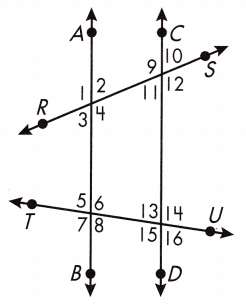
Question 4.
∠5 and ∠16 _____ _____
Answer: \(\overleftrightarrow{TU}\), alternate exterior
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 5.
∠13 and ∠8 _____ _____
Answer: \(\overleftrightarrow{TU}\), alternate interior
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 6.
∠15 and ∠10 _____ _____
Answer: \(\overleftrightarrow{CD}\), alternate exterior
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 7.
∠7 and ∠14 _____ _____
Answer: \(\overleftrightarrow{TU}\), alternate exterior
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 8.
∠8 and ∠16 _____ _____
Answer: \(\overleftrightarrow{TU}\), corresponding
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 9.
∠6 and ∠3 _____ _____
Answer: \(\overleftrightarrow{AB}\), alternate interior
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 10.
∠12 and ∠13 _____ _____
Answer: \(\overleftrightarrow{CD}\), alternate interior
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 11.
∠10 and ∠2 _____ _____
Answer: \(\overleftrightarrow{RS}\), corresponding
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Question 12.
∠5 and ∠13 _____ _____
Answer: \(\overleftrightarrow{TU}\), corresponding
A transversal is a line that intersects two or more lines at different points. The angles that are formed are called alternate interior angles and alternate exterior angles. When a transversal intersects parallel lines, corresponding angles are formed.
Adjacent angles are any 2 angles that are next to one another. In the figure, ∠1 and ∠2 are adjacent. ∠2 and ∠4 are also adjacent. Adjacent angles share a ray. Supplementary angles are two angles that equal 180°.
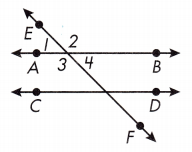
Question 1.
Name the pairs of adjacent angles in the figure.
Alternate interior angles are those that are inside the parallel lines and opposite one another. ∠3 and ∠5 are alternate interior angles. Alternate interior angles are congruent.
Answer: ∠1/∠2, ∠3/∠4, ∠5/∠6, ∠7/∠8, ∠1/∠4, ∠2/∠3, ∠5/∠8, ∠6/∠7
Alternate interior angles are those that are inside the parallel lines and opposite one another. Alternate interior angles are congruent.
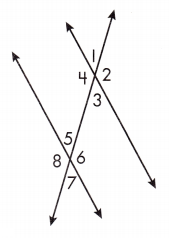
Question 2.
Name another pair of alternate interior angles in the figure. ![]()
Alternate exterior angles are those that are outside the parallel lines and opposite one another. ∠1 and ∠7 are alternate exterior angles. Alternate exterior angles are also congruent.
Answer: ∠4/ ∠6
Alternate exterior angles are those that are outside the parallel lines and opposite one another. Alternate interior angles are congruent.
Question 3.
Name another pair of alternate exterior angles in the figure. ![]()
Answer: ∠2/ ∠8
Alternate exterior angles are those that are outside the parallel lines and opposite one another. Alternate interior angles are congruent.
Look at the figure. List the following pairs of angles.
Question 4.
Adjacent:
Answer: ∠1/ ∠2, ∠2/∠4, ∠6/∠8, ∠8/∠7, ∠7/∠5, ∠3/∠1, ∠5/∠6, ∠3/∠4
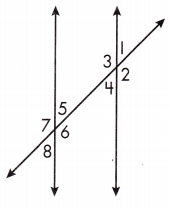
Question 5.
Alternate interior: ![]()
Answer: ∠3/∠6, ∠4/ ∠5
Question 6.
Alternate exterior: ![]()
Answer: ∠1/∠8, ∠2/∠7
Question 7.
Vertical:
Answer: ∠1/ ∠4, ∠2/∠3, ∠5/∠8, ∠6/∠7
Use the figures below to answer the questions.
Question 1.
If the measure of ∠1 is 45°, what is the measure of ∠4? __________
Answer: 45°
If the measure of ∠1 is 45°, then the measure of ∠4 is 45°.
Question 2.
If the measure of ∠12 is 102°, what is the measure of ∠11? ______
Answer: 78°
If the measure of ∠12 is 102°, then the measure of ∠11 is 78°.
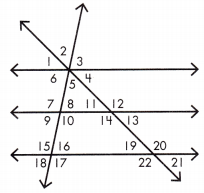
Question 3.
If the measure of ∠18 is 76°, what is the measure of ∠8? _________
Answer: 76°
If the measure of ∠18 is 76°, then the measure of ∠8 is 76°.
Question 4.
If the measure of ∠9 is 97°, what is the measure of ∠10? ______
Answer: 83°
If the measure of ∠9 is 97°, then the measure of ∠10 is 83°.
Question 5.
If the measure of ∠2 is 115°, what is the measure of ∠12? _____
Answer: 115°
If the measure of ∠2 is 115°, then the measure of ∠12 is 115°.
Question 6.
If the measure of ∠6 is 84°, what is the measure of ∠13? _____
Answer: 96°
If the measure of ∠6 is 84°, then the measure of ∠13 is 96°.
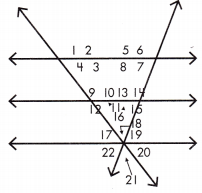
Question 7.
If the measure of ∠18 is 35°, what is the measure of ∠21? _____
Answer: 35°
If the measure of ∠18 is 35°, then the measure of ∠21 is 35°.
Question 8.
If the measure of ∠15 is 102°, what is the measure of ∠5? ____
Answer: 102°
If the measure of ∠15 is 102°, then the measure of ∠5 is 102°.
Question 9.
If ∠x = 70°, what is the measure of ∠y? ______
Answer: 70°
If ∠x = 70°, then the measure of ∠y is 70°.
Question 10.
If ∠x = 80°, what is the measure of ∠y? ______
Answer: 80°
If ∠x = 80°, then the measure of ∠y is 80°.
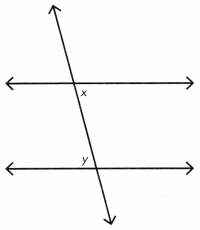
Question 11.
If ∠y = 75°, what is the measure of ∠x? __________
Answer: 75°
If ∠y = 75°, then the measure of ∠x is 75°.
Question 12.
If ∠y = 85°, what ¡s the measure of ∠x? _____
Answer: 85°
If ∠y = 85°, then the measure of ∠x is 85°.
Question 13.
If ∠5 = 100°, what is the measure of ∠15? _____
Answer: 80°
If ∠5 = 100°, then the measure of ∠15 is 80°.
Question 14.
If ∠6 = 70°, what is the measure of ∠13? _______
Answer: 110°
If ∠6 = 70°, then the measure of ∠13 is 110°.
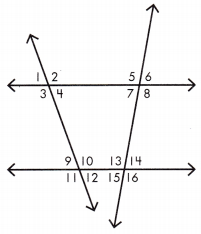
Question 15.
If ∠2 = 110°, what ¡s the measure of ∠9? _____
Answer: 70°
If ∠2 = 110°, then the measure of ∠9 is 70°.
Question 16.
If ∠4 = 85°, what ¡s the measure of ∠11? _________
Answer: 95°
If ∠4 = 85°, then the measure of ∠11 is 95°.
Question 17.
Can you determine the measure of ∠11 if you know the measure of ∠6? Why or why not?
Answer: No, we cannot determine.
Because those angles are different transversals.
Must Read: