Students can use the Spectrum Math Grade 8 Answer Key Chapter 5 Lesson 5.5 Slope and Similar Triangles as a quick guide to resolve any of their doubts.
Spectrum Math Grade 8 Chapter 5 Lesson 5.5 Slope and Similar Triangles Answers Key
The rate of change, or slope, of a line can be tested for constancy by using similar triangles.
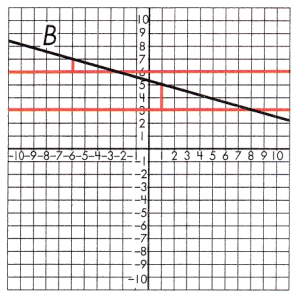
To test if the slope of the line 6 is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to line 8 to create a set of right triangles.
Find the length of the legs for each set of triangles. 3 & 1 and 6 & 2
Test the leg lengths for proportionality. \(\frac{3}{1}\) = \(\frac{6}{2}\)
3 × 2 = 6 and 6 × 1 = 6
These leg lengths are proportional, so the line has a constant slope.
Use similar right triangles to prove that each line has a constant slope.
Question 1.
a.
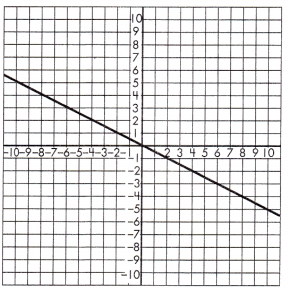
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
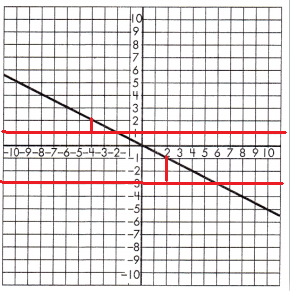
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
2 & 1
Triangle 2 Legs:
4 & 2
Proportionality Test:
\(\frac{2}{1}\) = \(\frac{4}{2}\)
2 × 2 = 4 and 4 × 1 = 4
These leg lengths are proportional, so the line has a constant slope.
b.
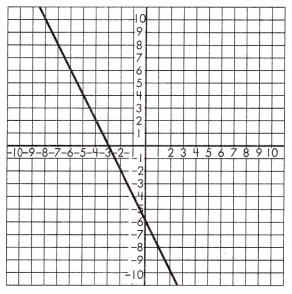
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
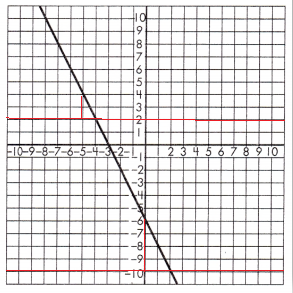
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
1 & 2
Triangle 2 Legs:
2 & 4
Proportionality Test:
\(\frac{1}{2}\) = \(\frac{2}{4}\)
2 × 2 = 4 and 4 × 1 = 4
These leg lengths are proportional, so the line has a constant slope.
Question 2.
a.
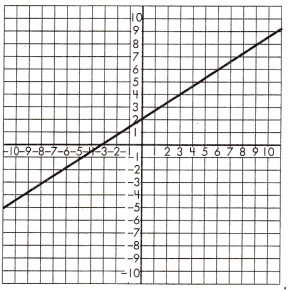
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
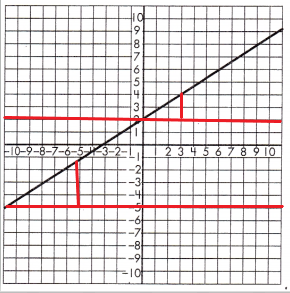
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
3 & 2
Triangle 2 Legs:
6 & 4
Proportionality Test:
\(\frac{3}{2}\) = \(\frac{6}{4}\)
3 × 4 = 12 and 6 × 2 = 12
These leg lengths are proportional, so the line has a constant slope.
b.
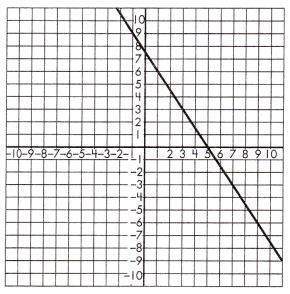
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
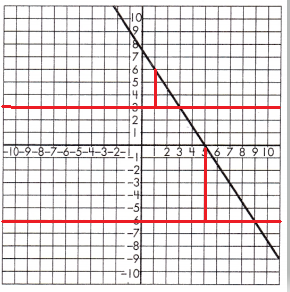
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
3 & 2
Triangle 2 Legs:
6 & 4
Proportionality Test:
\(\frac{2}{3}\) = \(\frac{4}{6}\)
3 × 4 = 12 and 6 × 2 = 12
These leg lengths are proportional, so the line has a constant slope.
Use similar right triangles to prove that each line has a constant slope.
Question 1.
a.
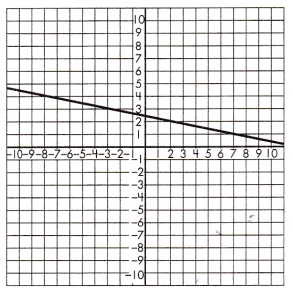
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
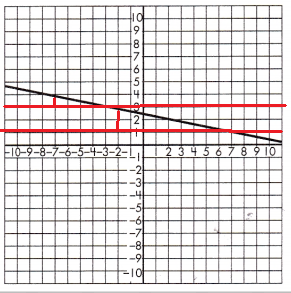
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
4 & 1
Triangle 2 Legs:
8 & 2
Proportionality Test:
\(\frac{4}{1}\) = \(\frac{8}{2}\)
4 × 2 = 8 and 8 × 1 = 8
These leg lengths are proportional, so the line has a constant slope.
b.
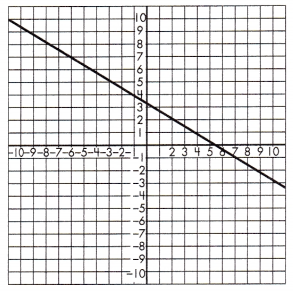
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
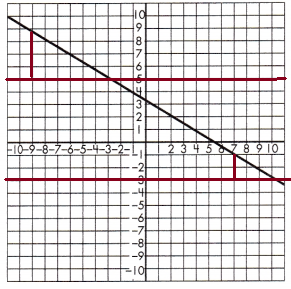
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
3 & 2
Triangle 2 Legs:
6 & 4
Proportionality Test:
\(\frac{3}{2}\) = \(\frac{6}{4}\)
3 × 4 = 12 and 6 × 2 = 12
These leg lengths are proportional, so the line has a constant slope.
Question 2.
a.
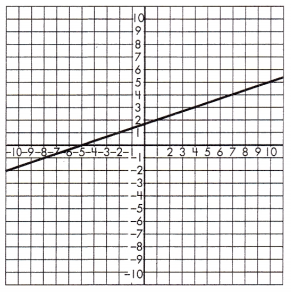
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
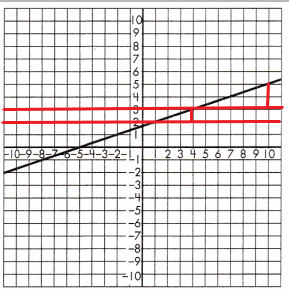
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
3 & 1
Triangle 2 Legs:
6 & 2
Proportionality Test:
\(\frac{3}{1}\) = \(\frac{6}{2}\)
3 × 2 = 6 and 6 × 1 = 6
These leg lengths are proportional, so the line has a constant slope.
b.
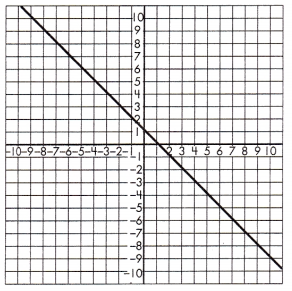
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
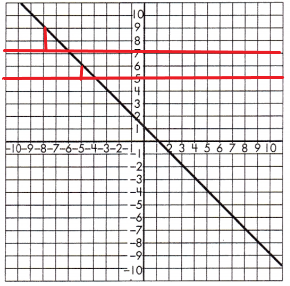
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
1 & 1
Triangle 2 Legs:
2 & 2
Proportionality Test:
\(\frac{1}{1}\) = \(\frac{2}{2}\)
1 × 2 = 2 and 1 × 2 = 2
These leg lengths are proportional, so the line has a constant slope.
Question 3.
a.
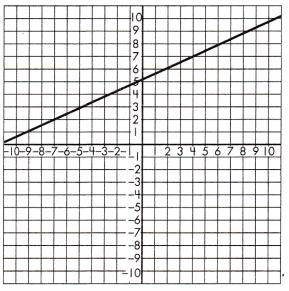
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
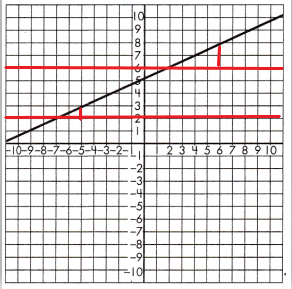
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
2 & 1
Triangle 2 Legs:
4 & 2
Proportionality Test:
\(\frac{2}{1}\) = \(\frac{4}{2}\)
2 × 2 = 4 and 4 × 1 = 4
These leg lengths are proportional, so the line has a constant slope.
b.
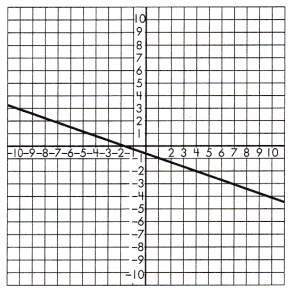
Triangle 1 Legs:
____ & _____
Triangle 2 Legs:
____ & _____
Proportionality Test:
____ = _____
Answer:
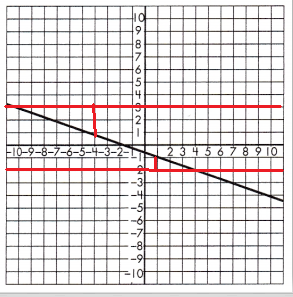
To test if the slope of the line is constant, draw a set of parallel lines that intersect the line.
Then, draw a line segment from each of the parallel lines to create a set of right triangles.
Find the length of the legs for each set of triangles.
Triangle 1 Legs:
3 & 1
Triangle 2 Legs:
6 & 2
Proportionality Test:
\(\frac{3}{1}\) = \(\frac{6}{2}\)
3 × 2 = 6 and 6 × 1 = 6
These leg lengths are proportional, so the line has a constant slope.