Students can use the Spectrum Math Grade 8 Answer Key Chapter 4 Lesson 4.10 Comparing Functions as a quick guide to resolve any of their doubts.
Spectrum Math Grade 8 Chapter 4 Lesson 4.10 Comparing Functions Answers Key
Functions that are represented in different ways can be compared by their rate of change or by specific values at a certain point. The functions do not have to be in the same format in order to compare them.
Which function has a greater rate of change?
y = –\(\frac{16}{5}\) + 6 or

Rate of change for table = \(\frac{-7-1}{2-0}\) = – \(\frac{8}{2}\) = -4
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the table is larger than the rate of change shown by the equation.
Compare the rate of change for the equations and tables shown below and decide which has a greater rate of change by writing equation or table.
Question 1.
a. y = 2x + 6 or
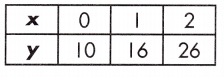
Answer:
Table.
Explanation:
Rate of change for table = \(\frac{26-10}{2-0}\) = \(\frac{16}{2}\) = 8
Rate of change for equation,
y = 2x + 6
y = (2 x 0) + 6
y = 6
Rate of change for table,
y = mx + b
10 = (8 x 0) + b
b = 10
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the table is larger than the rate of change shown by the equation.
b. y = 4x + 7 or
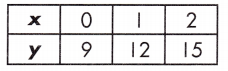
Answer:
Equation.
Explanation:
Rate of change for table = \(\frac{15-9}{2-0}\) = \(\frac{6}{2}\) = 3
Rate of change for equation,
y = 4x + 7
y = mx + b
Rate of change for equation m = 4
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the equation is larger than the rate of change shown by the table.
Question 2.
a. y = 7x + 4 or
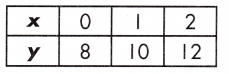
Answer:
Equation.
Explanation:
Rate of change for table = \(\frac{12-8}{2-0}\) = \(\frac{4}{2}\) = 2
Rate of change for equation,
y = 7x + 4
y = mx + b
Rate of change for equation m = 7
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the equation is larger than the rate of change shown by the table.
b. y = 3x + 4 or
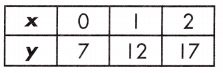
Answer:
Table.
Explanation:
Rate of change for table = \(\frac{17-7}{2-0}\) = \(\frac{10}{2}\) = 5
Rate of change for equation,
y = 3x + 4
y = mx + b
Rate of change for equation m = 3
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the table is larger than the rate of change shown by the equation.
Question 3.
a. y = 5x + 2 or
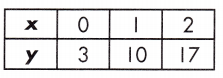
Answer:
Table.
Explanation:
Rate of change for table = \(\frac{17-3}{2-0}\) = \(\frac{14}{2}\) = 7
Rate of change for equation,
y = 5x + 2
y = mx + b
Rate of change for equation m = 5
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the table is larger than the rate of change shown by the equation.
b. y = \(\frac{3}{2}\)x – 2 or
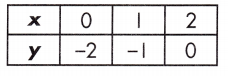
Answer:
Equation.
Explanation:
Rate of change for table = \(\frac{0-(-2)}{2-0}\) = \(\frac{2}{2}\) = 1
Rate of change for equation,
y = \(\frac{3}{2}\)x – 2
y = mx + b
Rate of change for equation m = \(\frac{3}{2}\)
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the equation is larger than the rate of change shown by the table.
Question 4.
a. y = 7x + 4 or
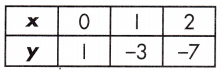
Answer:
Equation.
Explanation:
Rate of change for table = \(\frac{-7-1}{2-0}\) = \(\frac{8}{2}\) = 4
Rate of change for equation,
y = 7x + 4
y = mx + b
Rate of change for equation m = 7
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the equation is larger than the rate of change shown by the table.
b. y = \(\frac{3}{2}\)x + 2 or
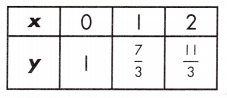
Answer:
Equation.
Explanation:
Rate of change for table = \(\frac{11}{3}\) – 1 = 10
\(\frac{10}{2}\) = 5
Rate of change for equation,
y = \(\frac{3}{2}\)x + 2
y = mx + b
Rate of change for equation m = \(\frac{3}{2}\)
Rate of change is judged by larger absolute value, therefore, the rate of change for the function represented in the equation and table are same.
Functions represented in a table and an equation can be compared when the value of x is provided. In the example below, you are given the value of x, which can be substituted into each equation to determine which function has the greater value.
y = –\(\frac{16}{5}\)x + 6
or
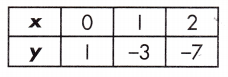
when x = 2
Step 1: Substitute 2 for x in the equation and solve the first function.
y = –\(\frac{16}{5}\)(2) + 6
y = -6\(\frac{2}{5}\) + 6
y = –\(\frac{2}{5}\)
Step 2: Find the rate of change for the table.
![]()
Step 3: Find the y-intercept of the table.
This is found on the table where x = 0. x = 0 where y = 1
Step 4: Substitute the rate of change, the given value of x, and the y-intercept into the equation y = mx + b.
y = mx + b
y = (-4)(2) + 1
y = -7
Step 5: Compare the value of y in the formula to the value of y in the table to determine which function has the greater value.
Equation: y = \(\frac{-2}{5}\) Table: y = -7
Therefore, the function shown in the equation has a greater value.
Which function has a greater value for the given value of x? Write equation, table, or equal.
Question 1.
a.
y = 2x + 6 or when x = 1
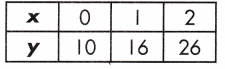
Answer:
Table.
Explanation:
Step 1: Substitute 1 for x in the equation and solve the first function.
y = 2x + 6
y = 2 + 6
y = 8
Step 2: Find the rate of change for the table.
m= \(\frac{26-10}{2-0}\) = \(\frac{16}{2}\) = 8
Step 3: Find the y-intercept of the table.
This is found on the table where x = 0.
x = 0 where y = 10
Step 4: Substitute the rate of change, the given value of x, and the y-intercept into the equation y = mx + b.
y = mx + b
y = (8)(1) + 10
y = 18
Step 5: Compare the value of y in the formula to the value of y in the table to determine which function has the greater value.
Equation: y = 8; Table: y = 18
Therefore, the function shown in the table has a greater value.
b.
y = 4x + 7 or when x = 2
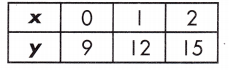
Answer:
Equal.
Explanation:
Given, 4x + 7
Step 1: Substitute 2 for x in the equation and solve the first function.
y = (4 x 2) + 7
y = 8 + 7
y = 15
Step 2: Find the rate of change for the table.
\(\frac{15-9}{2-0}\) = \(\frac{6}{2}\) = 3
Step 3: Find the y-intercept of the table.
This is found on the table where x = 0. x = 0 where y = 9
Step 4: Substitute the rate of change, the given value of x, and the y-intercept into the equation y = mx + b.
y = mx + b
y = (3)(2) + 9
y = 6 + 9 = 15
Step 5: Compare the value of y in the formula to the value of y in the table to determine which function has the greater value.
Equation: y = 15; Table: y = 15
Therefore, the function shown in the equation has a greater value.
Question 2.
a.
y = 7x + 4 or when x = 3
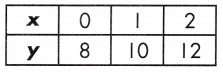
Answer:
Equation.
Explanation:
Step 1: Substitute 3 for x in the equation and solve the first function.
y = 7x + 4
y = (7 x 3) + 4
y = 21 + 4
y = 25
Step 2: Find the rate of change for the table.
\(\frac{12-8}{2-0}\) = \(\frac{4}{2}\) = 2
Step 3: Find the y-intercept of the table.
This is found on the table where x = 0. x = 0 where y = 8
Step 4: Substitute the rate of change, the given value of x, and the y-intercept into the equation y = mx + b.
y = mx + b
y = (2)(3) + 8
y = 6 + 8
y = 14
Step 5: Compare the value of y in the formula to the value of y in the table to determine which function has the greater value.
Equation: y = 25; Table: y = 14
Therefore, the function shown in the equation has a greater value.
b.
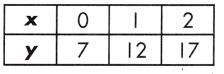
y = 3x + 4 or when x = 0
Answer:
Table.
Explanation:
Step 1: Substitute 0 for x in the equation and solve the first function.
y = 3x + 4
y = 4
Step 2: Find the rate of change for the table.
\(\frac{17-7}{2-0}\) = \(\frac{10}{2}\) = 5
Step 3: Find the y-intercept of the table.
This is found on the table where x = 0. x = 0 where y = 7
Step 4: Substitute the rate of change, the given value of x, and the y-intercept into the equation y = mx + b.
y = mx + b
y = (5)(0) + 7
y = 7
Step 5: Compare the value of y in the formula to the value of y in the table to determine which function has the greater value.
Equation: y = 4; Table: y = 7
Therefore, the function shown in the table has a greater value.
Question 3.
a.
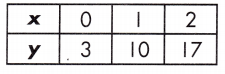
y = 5x + 2 or when x = -3
Answer:
Equation.
Explanation:
Step 1: Substitute -3 for x in the equation and solve the first function.
y = 5x + 2
y = (5)(-3) + 2
y = -15 + 2
y = -13
Step 2: Find the rate of change for the table.
\(\frac{17-3}{2-0}\) = \(\frac{14}{2}\) = 7
Step 3: Find the y-intercept of the table.
This is found on the table where x = 0. x = 0 where y = 3
Step 4: Substitute the rate of change, the given value of x, and the y-intercept into the equation y = mx + b.
y = mx + b
y = (3)(-3) + 3
y = -9 + 3
y = -6
Step 5: Compare the value of y in the formula to the value of y in the table to determine which function has the greater value.
Equation: y = -13; Table: y = -6
Therefore, the function shown in the equation has a greater value.
b.
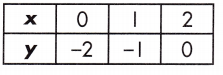
y = x – 2 or when x = 4
Answer:
Equal.
Explanation:
Step 1: Substitute 4 for x in the equation and solve the first function.
y = x – 2
y = 4 – 2
y = 2
Step 2: Find the rate of change for the table.
\(\frac{0-(-2)}{2-0}\) = \(\frac{2}{2}\) = 1
Step 3: Find the y-intercept of the table.
This is found on the table where x = 0. x = 0 where y = -2
Step 4: Substitute the rate of change, the given value of x, and the y-intercept into the equation y = mx + b.
y = mx + b
y = (1)(4) – 2
y = 4 – 2
Step 5: Compare the value of y in the formula to the value of y in the table to determine which function has the greater value.
Equation: y = 2; Table: y = 2
Therefore, the function shown in the equation and table are equal.
Functions represented on a graph can be compared to functions represented by an equation.
Which function has a greater rate of change?
y = -2x + 3 or
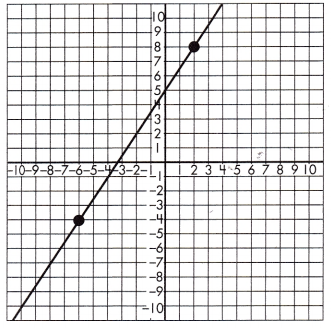
Step 1: Identify the slope, or rate of change, for the function represented by the equation. In this case, the rate of change is -2.
Step 2: Identify two points on the line and calculate the rate of change, or slope, for the function represented by the graph. In this case: \(\frac{8-(-4)}{2-(-6)}\) = \(\frac{12}{8}\) = \(\frac{3}{2}\)
Step 3: Compare the rates of change to see which is greater. The absolute value of -2 is greater than \(\frac{3}{2}\), therefore the function represented by the equation has a greater rate of change.
Which function has a greater rate of change? Write equation, graph, or equal.
Question 1.
a.
y = \(\frac{1}{2}\)x – 2 or
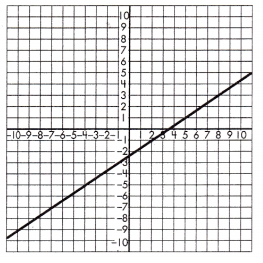
______________
Answer:
Graph.
Explanation:
Step 1: The slope, or rate of change, for the function represented by the equation.
In this case of equation y = \(\frac{1}{2}\)x – 2
As we now, m is slope of the equation y = mx + b
The rate of change is \(\frac{1}{2}\).
Step 2: Identify two points on the line and calculate the rate of change, or slope, for the function represented by the graph.
In this case:
The two points are (-7, -7) and (5, 1).
\(\frac{1-(-7)}{5 – (-7)}\) = \(\frac{8}{12}\) = \(\frac{2}{3}\)
Step 3: Compare the rates of change to see which is greater.
The absolute value of \(\frac{2}{3}\) is greater than \(\frac{1}{2}\),
therefore the graph has a greater rate of change.
b. y = -6x + 1 or
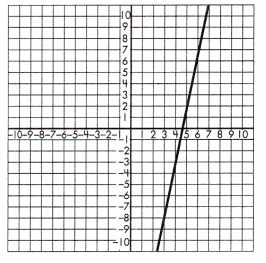
______________
Answer:
Equation.
Explanation:
Step 1: Identify the slope, or rate of change, for the function represented by the equation.
In this case of the equation y = -6x + 1
As we now, m is slope of the equation y = mx + b
The rate of change is -6.
Step 2: Identify two points on the line and calculate the rate of change, or slope, for the function represented by the graph.
In this case:
The two points are (4, -3) and (6, 6).
\(\frac{6-(-3)}{6-4}\) = \(\frac{9}{2}\) = 4\(\frac{1}{2}\)
Step 3: Compare the rates of change to see which is greater.
The absolute value of -6 is greater than 4\(\frac{1}{2}\),
therefore the function represented by the equation has a greater rate of change.
c. y = 3x – 2 or
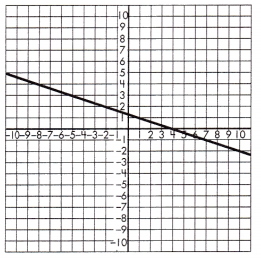
______________
Answer:
Equation.
Explanation:
Step 1: Identify the slope, or rate of change, for the function represented by the equation.
In this case of the equation y = 3x – 2
As we now, m is slope of the equation y = mx + b
So, the rate of change is 3.
Step 2: Identify two points on the line and calculate the rate of change, or slope, for the function represented by the graph.
In this case:
The two points are (4, -3) and (6, 6).
\(\frac{6-(-3)}{6-4}\) = \(\frac{9}{2}\) = 4\(\frac{1}{2}\)
Step 3: Compare the rates of change to see which is greater.
The absolute value of -6 is greater than 4\(\frac{1}{2}\),
therefore the function represented by the equation has a greater rate of change.
Question 2.
a.
y = 4x + 3 or
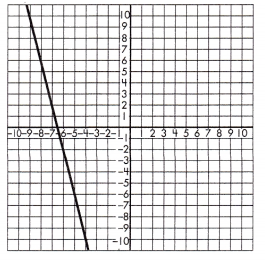
______________
Answer:
Equation.
Explanation:
Step 1: Identify the slope, or rate of change, for the function represented by the equation.
In this case of the equation y = 4x + 3
As we now, m is slope of the equation y = mx + b
So, the rate of change is 4.
Step 2: Identify two points on the line and calculate the rate of change, or slope, for the function represented by the graph.
In this case:
The two points are (-7, 2) and (-10, -4).
\(\frac{-4- 2}{-10 – (-7)}\) = –\(\frac{6}{3}\) = – 2
Step 3: Compare the rates of change to see which is greater.
The absolute value of 4 is greater than –\(\frac{10}{13}\),
therefore the function represented by the equation has a greater rate of change.
b.
y = –\(\frac{2}{3}\)x + 2 or
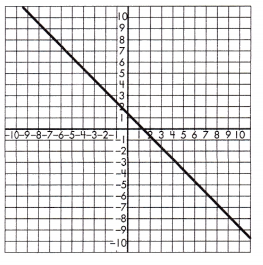
______________
Answer:
Graph.
Explanation:
Step 1: The slope, or rate of change, for the function represented by the equation.
In this case of equation y = –\(\frac{2}{3}\)x + 2
As we now, m is slope of the equation y = mx + b
So, the rate of change is –\(\frac{2}{3}\).
Step 2: Identify two points on the line and calculate the rate of change, or slope, for the function represented by the graph.
In this case:
Two points are (4, -3) and (6, -5).
\(\frac{-5-(-3)}{6 – 4}\) = \(\frac{-2}{2}\) = -1
Step 3: Compare the rates of change to see which is greater.
The absolute value of \(\frac{2}{3}\) is greater than –\(\frac{2}{3}\),
therefore the graph has a greater rate of change.
c.
y = 2x – 5 or
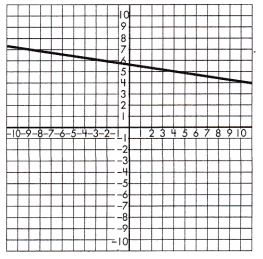
______________
Answer:
Equation.
Explanation:
Step 1: The slope, or rate of change, for the function represented by the equation.
In this case of equation y = 2x – 5
As we now, m is slope of the equation y = mx + b
So, the rate of change is 2.
Step 2: Identify two points on the line and calculate the rate of change, or slope, for the function represented by the graph.
In this case:
The two points are (-8, 7) and (10, 4).
\(\frac{4 – 7)}{10 – 7}\) = \(\frac{-3}{3}\) = -1
Step 3: Compare the rates of change to see which is greater.
The absolute value of 2 is greater than -1,
therefore the equation has a greater rate of change.