Spectrum Math Grade 8 Chapter 2 Pretest Answer Key

Students can use the Spectrum Math Grade 8 Answer Key Chapter 2 Pretest as a quick guide to resolve any of their doubts.

Spectrum Math Grade 8 Chapter 2 Pretest Answers Key

Check What You Know

Rational and Irrational Number Relationships

Evaluate each expression.

Question 1.
a.
= ____
Answer: 5
The square root of a number is the number that, multiplied by itself, equals that number. The square root of 25 is 5.
=  5.
Numbers that have a whole number as their square root are called perfect squares. The expression of a square root is called a radical. The symbol  is called a radical sign. When a number is not a perfect square, you can estimate its square root by determining which perfect squares it comes between.

b.
= ____
Answer: 3
The square root of a number is the number that, multiplied by itself, equals that number. The square root of 9 is 3.  =  3.
Numbers that have a whole number as their square root are called perfect squares. The expression of a square root is called a radical. The symbol  is called a radical sign. When a number is not a perfect square, you can estimate its square root by determining which perfect squares it comes between.

c.

Answer: 10
The square root of a number is the number that, multiplied by itself, equals that number. The square root of 100 is 10.
=  10.
Numbers that have a whole number as their square root are called perfect squares. The expression of a square root is called a radical. The symbol  is called a radical sign. When a number is not a perfect square, you can estimate its square root by determining which perfect squares it comes between.

Question 2.
a.
= ____
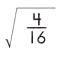Answer: \(\frac{2}{4}\)
The square root of a number is the number that, multiplied by itself, equals that number.
= \(\frac{2}{4}\)
Numbers that have a whole number as their square root are called perfect squares. The expression of a square root is called a radical. The symbol  is called a radical sign. When a number is not a perfect square, you can estimate its square root by determining which perfect squares it comes between.

b. = ____
Answer: 9
The square root of a number is the number that, multiplied by itself, equals that number. The square root of 81 is 9.
 =  9.
Numbers that have a whole number as their square root are called perfect squares. The expression of a square root is called a radical. The symbol  is called a radical sign. When a number is not a perfect square, you can estimate its square root by determining which perfect squares it comes between.

c. = ____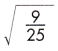
Answer: \(\frac{3}{5}\)
The square root of a number is the number that, multiplied by itself, equals that number.
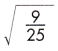= \(\frac{3}{5}\)
Numbers that have a whole number as their square root are called perfect squares. The expression of a square root is called a radical. The symbol  is called a radical sign. When a number is not a perfect square, you can estimate its square root by determining which perfect squares it comes between.

Question 3.
a.

Answer: 7
The cube of a number is that number multiplied by itself three times. A cube is expressed as n³, which means n × n × n or n cubed. The cube root of a number is the number that, multiplied by itself and by itself again, equals that number. The cube root of 343 is 7.
 = 7
The expression of a cube root is called a radical. The symbol  is called a radical sign. The 3 on the radical sign shows that this is a cube root.

b.

Answer: 9
The cube of a number is that number multiplied by itself three times. A cube is expressed as n³, which means n × n × n or n cubed. The cube root of a number is the number that, multiplied by itself and by itself again, equals that number. The cube root of 729 is 9.
 = 9
The expression of a cube root is called a radical. The symbol  is called a radical sign. The 3 on the radical sign shows that this is a cube root.

c.

Answer: 4
The cube of a number is that number multiplied by itself three times. A cube is expressed as n³, which means n × n × n or n cubed. The cube root of a number is the number that, multiplied by itself and by itself again, equals that number. The cube root of 64  is 4.
 = 4
The expression of a cube root is called a radical. The symbol  is called a radical sign. The 3 on the radical sign shows that this is a cube root.

Question 4.
a.

Answer: 6
The cube of a number is that number multiplied by itself three times. A cube is expressed as n³, which means n × n × n or n cubed. The cube root of a number is the number that, multiplied by itself and by itself again, equals that number. The cube root of 216 is 6.
 = 6
The expression of a cube root is called a radical. The symbol  is called a radical sign. The 3 on the radical sign shows that this is a cube root.

b.

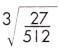
Answer: \(\frac{3}{8}\)
Fractions can also have cube roots.
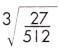= \(\frac{3}{8}\)
because \(\frac{3}{8}\) x \(\frac{3}{8}\) x \(\frac{3}{8}\) = \(\frac{27}{512}\)

c.

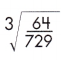
Answer: \(\frac{4}{9}\)
Fractions can also have cube roots.
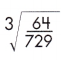= \(\frac{4}{9}\)
because \(\frac{4}{9}\) x \(\frac{4}{9}\) x \(\frac{4}{9}\) = \(\frac{64}{729}\)

Approximate the value of each expression.

Question 5.
The value of is between ___ and ____
Answer: The value of  is something between 3 and 4.
Look at the squares of 3.1 and 3.2.
3.1² = 9.61
3.2² = 10.24
By looking at these squares, it is evident that  is between 3.1 and 3.2.

Question 6.
The value of is between ___ and ____
Answer: The value of is something between 4 and 5.
Look at the squares of 4.1 and 4.2.
4.1³ = 68.921
4.2³ = 74.088
By looking at these squares, it is evident that is between 4.1 and 4.2.

Question 7.
The value of is between ___ and ____
Answer: The value of is something between 6 and 7.
Look at the squares of 6.5 and 6.6.
6.5² = 42.25
6.6² = 43.56
By looking at these squares, it is evident that is between 6.5 and 6.6.

Question 8.
The value of is between ___ and ____
Answer: The value of is something between 2 and 3.
Look at the squares of 2.5 and 2.6.
2.5³ = 15.625
2.6³ = 17.576
By looking at these squares, it is evident that is between 2.5 and 2.6.

Question 9.
The value of is between ___ and ____
Answer: The value of is something between 1 and 2.
Look at the squares of 1.2 and 1.3.
1.2³ = 1.728
1.3³ = 2.197
By looking at these squares, it is evident that is between 1.2 and 1.3.

Question 10.
The value of is between ___ and ____
Answer: The value of is something between 4 and 5.
Look at the squares of 4.8 and 4.9.
4.8² = 23.04
4.9² = 24.01
By looking at these squares, it is evident that is between 4.8 and 4.9.

Use roots or exponents to solve each equation. Write fractions in simplest form.

Question 11.
a. x² = 64
x = ___
Answer:  x = 8
x² = 64
As the exponent is 2, so use the square root as the inverse operation.
Use root on both sides
\(\sqrt{x² }\) =\(\sqrt{64}\)
By simplification,
x = 8

b. = 9
x = ____
Answer:  x = 81
\(\sqrt{x}\)= 81
As the exponent is 2, so use the square root as the inverse operation.
Square both sides of the equation.
{\(\sqrt{x}\)}² = {9}²
By simplification,
x =  81

c. x³ = 343
x = ___
Answer: x = 7
As the exponent is 3, so use the cube root as the inverse operation.
Use root on both sides
\(\sqrt[3]{x³}\) = \(\sqrt[3]{343}\)
By simplification,
x  = 7

Question 12.
a.
= 6
x = ____
Answer: x = 216
\(\sqrt[3]{x}\) = 6
As the exponent is 3, so use the cube root as the inverse operation.
Square both sides of the equation.
{\(\sqrt[3]{x}\)}³ = {6}³
By simplification,
x = 216

b.
x² = 121
x = ____
Answer:  x = 11
x² = 121
As the exponent is 2, so use the square root as the inverse operation.
Use root on both sides
\(\sqrt{x² }\) =\(\sqrt{121}\)
By simplification,
x = 11

c. = 10
x = ____
Answer: x = 1000
\(\sqrt[3]{x}\) = 10
As the exponent is 3, so use the cube root as the inverse operation.
Square both sides of the equation.
{\(\sqrt[3]{x}\)}³ = {10}³
By simplification,
x = 1000

Compare using <, >, or =.

Question 13.
a. _____ \(\frac{2}{3}\)
Answer:  = \(\frac{2}{3}\)
This statement is true because is \(\frac{2}{3}\). Therefore, is equal to \(\frac{2}{3}\).

b. ____ 5
Answer: < 5
This statement is true because is 3.16. As 3.16 is less than 5. Therefore, is less than 5.

c. ____ 3
Answer: < 3
This statement is true because is 2.92. As 2.92 is less than  3. Therefore, is less than 3.

Question 14.
a. 1.2 ____
Answer: 1.2 <
This statement is true because is 2. As 1.2 is less than  2. Therefore, 1.2 is less than .

b. ___ 3.5
Answer:  > 3.5
This statement is true because is 3.9. As 3.9 is greater than 3.5. Therefore, is greater than 3.5.

c. ____ 4
Answer: < 4
This statement is true because is 3.33. As 3.33 is less than  4. Therefore, is less than 4 .

Question 15.
a. \(0 . \overline{33}\) _____
Answer: \(0 . \overline{33}\) <
This statement is true because is 0.57. As \(0 . \overline{33}\) is less than  0.57. Therefore, \(0 . \overline{33}\) is less than .

b. \(\frac{5}{6}\) ____
Answer: \(\frac{5}{6}\)  <
This statement is true because is 1.414 and  \(\frac{5}{6}\)  is 0.6. As 0.6  is less than  1.414. Therefore, \(\frac{5}{6}\)  is less than  .

c. ____ 3
Answer:  < 3
This statement is true because is 2.23. As 2.23  is less than 3 Therefore, is less than  3.

Put the values below in order from least to greatest along a number line.

Question 16.
14, , 4π

Answer:

Rational and irrational numbers can be compared by approximating their value and placing them along a number line.

Question 17.


Answer:

Rational and irrational numbers can be compared by approximating their value and placing them along a number line.

Question 18.
, 2, 5

Answer:

Rational and irrational numbers can be compared by approximating their value and placing them along a number line.