Spectrum Math Grade 7 Chapters 1-7 Final Test Answer Key

This handy Spectrum Math Grade 7 Answer Key Chapter 1-7 Final Test provides detailed answers for the workbook questions

Spectrum Math Grade 7 Chapter 1-7 Final Test Answers Key

Add, subtract, multiply, or divide.

Question 1.
a. 3 + (-7) = _____________
Answer:
3 + (-7)
+ × – = –
3 – 7 = -4
So, 3 + (-7) = -4

b. 2\(\frac{1}{4}\) + 2\(\frac{2}{3}\) = _____________
Answer:
Given,
2\(\frac{1}{4}\) + 2\(\frac{2}{3}\)
2 + \(\frac{1}{4}\) + 2 + \(\frac{2}{3}\)
Add whole numbers
2 + 2 = 4
Add the fractions
\(\frac{1}{4}\) + \(\frac{2}{3}\)
LCD is 12.
\(\frac{3}{12}\) + \(\frac{8}{12}\) = \(\frac{11}{12}\)
4 + \(\frac{11}{12}\) = 4\(\frac{11}{12}\)
2\(\frac{1}{4}\) + 2\(\frac{2}{3}\) = 4\(\frac{11}{12}\)

c. (-5) + 8 = _____________
Answer:
Given,
(-5) + 8
+ × – = –
-5 + 8 = 3

Question 2.
a. (-8) + 12 = _____________
Answer:
(-8) + 12
+ × – = –
-8 + 12 = 4

b. 9 + (-11) = _____________
Answer:
9 + (-11)
+ × – = –
9 – 11 = -2

c. (-7) + 2 = _____________
Answer:
(-7) + 2
+ × – = –
-7 + 2 = -5

Question 3.
a. 5 – 8 = _____________
Answer:
5 – 8 = -3
The greatest number has a negative sign so the result will be negative.

b. 6 – 5 = _____________
Answer:
6 – 5 = 1
The greatest number has a positive sign so the result will be positive.

c. |-2| – 8 = _____________
Answer:
|-2| = 2
2 – 8 = -6
The greatest number has a negative sign so the result will be negative.
|-2| – 8 = -6

Question 4.
a. 3\(\frac{3}{10}\) – 2 \(\frac{4}{5}\) = ______________
Answer:
Given,
3\(\frac{3}{10}\) – 2 \(\frac{4}{5}\)
3 + \(\frac{3}{10}\) – 2 – \(\frac{4}{5}\)
3 – 2 = 1
\(\frac{3}{10}\) – \(\frac{4}{5}\)
LCD is 10
\(\frac{3}{10}\) – \(\frac{8}{10}\) = –\(\frac{5}{10}\) = –\(\frac{1}{2}\)
1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
3\(\frac{3}{10}\) – 2 \(\frac{4}{5}\) = \(\frac{1}{2}\)

b. (-6) – 5 = _____________
Answer:
Given,
(-6) – 5
– × – = +
-6 – 5 = -11

c. 5 – 6 = _____________
Answer:
Given,
5 – 6
The greatest number has a negative sign so the result will be negative.
5 – 6 = -1

Question 5.
a. (23) × (-3) = _____________
Answer:
Given,
(23) × (-3)
+ × – = –
23 × -3 = -69
By multiplying 23 and -3 we get -69.

b. 45 × 8 = _______________
Answer:
Given,
45 × 8 = 360
By multiplying 45 and 8 we get 360.

c. (-18) × (-6) = ______________
Answer:
Given,
(-18) × (-6)
– × – = +
18 × 6 = 108
By multiplying 18 and 6 we get 108.

Question 6.
a. 71 × (-5) = ______________
Answer:
Given,
71 × (-5)
+ × – = –
71 × -5 = -355

b. (-83) × 7 = ______________
Answer:
Given,
(-83) × 7
+ × – = –
-83 × 7 = -581
By multiplying 83 and 7 we get -581.

c. \(\frac{4}{5}\) × \(\frac{1}{8}\) = _____________
Answer:
Given,
\(\frac{4}{5}\) × \(\frac{1}{8}\) = \(\frac{4×1}{5×8}\) = \(\frac{4}{40}\) = \(\frac{1}{10}\)
\(\frac{4}{5}\) × \(\frac{1}{8}\) = \(\frac{1}{10}\)

Question 7.
a. (-24) ÷ (-4) = ______________
Answer:
Given,
(-24) ÷ (-4)
– ÷ – = +
24 ÷ 4 = 6
By dividing 24 by 4 we get 6.

b. 45 ÷ (-9) = ______________
Answer:
45 ÷ (-9)
+ ÷ – = –
45 ÷ -9 = -5
By diving 45 by 9 we get 5.
45 ÷ (-9) = -5

c. (-95) ÷ 5 = ______________
Answer:
Given,
(-95) ÷ 5
+ ÷ – = –
-95 ÷ 5 = -19
By dividing 95 and 5 we get 19.
(-95) ÷ 5 = -19.

Question 8.
a. (-22) ÷ (-1) = _____________
Answer:
Given,
(-22) ÷ (-1)
– ÷ – = +
-22 ÷ -1 = 22
By dividing 22 and 1 we get 22.

b. 42 ÷ (-7) = ______________
Answer:
Given,
42 ÷ (-7)
+ ÷ – = –
42 ÷ -7 = -6
By dividing 42 and 7 we get 6
42 ÷ (-7) = -6

c. (-81) ÷ 9 = _______________
Answer:
Given,
(-81) ÷ 9
+ ÷ – = –
81 ÷ 9 = 9
By dividing 81 and 9 we get 9.
-81 ÷ 9 = -9

Use long division to change each rational number into a decimal. Then, circle to indicate if each is terminating (T) or repeating (R).

Question 9.
a. \(\frac{3}{5}\) = _____________ T or R
Answer: 0.60

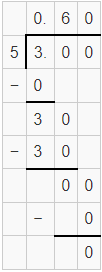
The given fraction is terminating (T).

b. \(\frac{7}{50}\) = ______________ T or R
Answer: 0.14

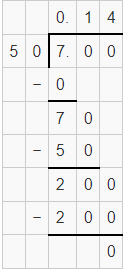
The given fraction is terminating (T).

c. \(\frac{1}{125}\) = ______________ T or R
Answer: 0.008

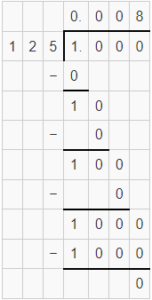
The given fraction is terminating (T).

Solve each problem. Use 3.14 for π when needed.

Question 10.
331 students went on a field trip. Six buses were filled and 7 students traveled in cars. How many students were in each bus?
Let s represent the number of students on each bus.
Equation: ___________________________
There were _____________ students on each bus.
Answer:
Given,
331 students went on a field trip.
Six buses were filled and 7 students traveled in cars.
Let s represent the number of students on each bus.
6s + 7 = 331
6s = 331 – 7
6s = 324
s = 324/6
s = 54
There are 54 students in each bus.

Question 11.
The length of a football field is 30 yards more than its width. If it is 100 yards long, how wide is the field?
Let w represent the width of the field.
Equation: ___________________________
The football field is _____________ yards wide.
Answer:
Given,
The length of a football field is 30 yards more than its width.
L = 100
L = 30 + W
100 = 30 + W
W = 100 – 30
W = 70 yards
Thus the width of the field is 70 yards.
The football field is 70 yards wide.

Question 12.
Julia has 3 red marbles, 4 blue marbles, 3 yellow marbles, and 6 black marbles. She takes one marble out of the bag at random.
The probability that it ¡s a black marble is _____________.
The probability that t is a yellow marble is _____________.
The probability that ¡t ¡s not o red marble is _____________.
Answer:
Given,
Julia has 3 red marbles, 4 blue marbles, 3 yellow marbles, and 6 black marbles.
She takes one marble out of the bag at random.
Total number of marbles = 3 + 4 + 3 + 6 = 16 marbles.
The probability that it is a black marble is 6/16
The probability that it is a yellow marble is 3/16
The probability that it is not o red marble is (4 + 3 + 6)/16 = 13/16

Question 13.
The municipal swimming pool is 50 meters long and 25 meters wide, and it is filled to a uniform depth of 3 meters. What is the volume of water in the pool?
The volume of the water is ____________ cubic meters.
Answer:
Given,
The municipal swimming pool is 50 meters long and 25 meters wide, and it is filled to a uniform depth of 3 meters.
1 cubic meter = 1000 liters
50 × 25 × 3 × 1000 = 3,750,000 liters
The volume of the water is 3750 cubic meters.

Question 14.
There are four hundred students at Thompson Middle School. If 54% of the students are female, what is the ratio of female students to male students?
The ratio of female to male students is _____________.
Answer:
Given,
There are four hundred students at Thompson Middle School.
54% = 54/100 = 0.54
0.54 × 400 = 216
400/216 = 1.85
The ratio of female to male students is 1:3

Question 15.
Ben is putting in a 7-foot diameter circular flower bed at his school. He wants to put plastic edging along the outside edge of the flower bed. How much edging will he need?
Ben will need _____________ feet of plastic edging.
Answer:
Given,
Ben is putting in a 7-foot diameter circular flower bed at his school.
He wants to put plastic edging along the outside edge of the flower bed.
C = πd
C = 3.14 × 7
C = 22
Ben will need 22 feet of plastic edging.

Write yes or no to tell if each set of ratios is proportional.

Question 16.
a. \(\frac{5}{4}\), \(\frac{35}{28}\)
Answer:
\(\frac{5}{4}\) = \(\frac{35}{28}\)
\(\frac{35}{28}\) × \(\frac{7}{7}\) = \(\frac{5}{4}\)
The ratio is proportional.

b. \(\frac{4}{3}\), \(\frac{24}{30}\)
Answer:
\(\frac{4}{3}\), \(\frac{24}{30}\)
\(\frac{24}{30}\) = \(\frac{4}{5}\)
\(\frac{4}{3}\) ≠ \(\frac{4}{5}\)
The ratio is not proportional.

c. \(\frac{6}{5}\), \(\frac{24}{20}\)
Answer:
\(\frac{6}{5}\), \(\frac{24}{20}\)
\(\frac{24}{20}\) = \(\frac{6}{5}\)
\(\frac{6}{5}\) = \(\frac{6}{5}\)
The ratio is proportional.

d. \(\frac{11}{3}\), \(\frac{33}{9}\)
Answer:
\(\frac{11}{3}\), \(\frac{33}{9}\)
\(\frac{33}{9}\) = \(\frac{11}{3}\)
\(\frac{11}{3}\) = \(\frac{11}{3}\)
The ratio is proportional.

Find the constant of proportionality for the set of values.

Question 17.

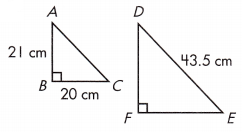
k = _____________
Answer:
The corresponding angles and sides will have the same ratio in similar triangles.
(20 × 20) + (21 × 21) = AC²
AC² = 400 + 441 = 841
AC = √841
AC = 29
DE/AC = 43.5/21 = 1.5
FE = 1.5 × BC
FE = 1.5 × 20 = 30
DF = 1.5 × AB
DF = 1.5 × 21 = 31.5
DE² = DF² + FE²
= 31.5² + 30²
= 992.25 + 900
= 1892.25
DE = √1892.25
DE = 43.5

These similar triangles are drawn to scale. Find the missing side lengths.

Question 18.
a.

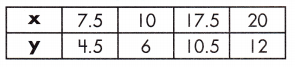
AC = _____________ cm
DF = _____________ cm
FE = _____________ cm
Answer:

b.

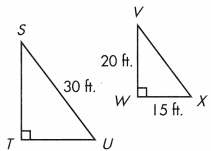
ST = _____________ ft.
TU = _____________ ft.
VX = _____________ ft.
Answer:
The corresponding angles and sides will have the same ratio in similar triangles.
VX² = 20² + 15²
VX² = 400 + 300
VX = √700
VX = 26.45 ft
SU/VX = 30/26.45
SU/VX = 1.13 ft
TU = 1.13 × 15
TU = 16.95 ft
ST = 20 × 1.13
ST =  22.6 ft

Find the area of each figure and the area and circumference of each circle. Use 3.14 for π. Round answers to the nearest hundredth.

Question 19.
a.

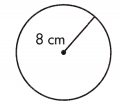
circumference: ______________ cm
area: ____________ sq. cm
Answer:
Given,
r = 8 cm
We know that,
C = 2πr
C = 2 × 3.14 × 8
C = 50.26 cm
A = πr²
A = 3.14 × 8²
A = 201.06 sq. cm

b.

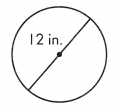
____________ in.
____________ sq. in
Answer:
Given,
d = 12 in.
r = d/2
r = 12/2 = 6 in.
We know that,
C = 2πr
C = 2 × 3.14 × 6
C = 37.7 in.
A = πr²
A = 3.14 × 6²
A = 3.14 × 36
A = 113.1 sq. in.

c.

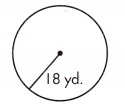
____________ yd
____________ sq. yd.
Answer:
Given,
r = 18 yd.
We know that,
C = 2πr
C = 2 × 3.14 × 18
C = 113.09 yd
A = πr²
A = 3.14 × 18²
A = 1017.88 sq. yd

Question 20.
a.

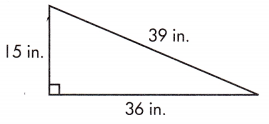
A = ____________ in.²
Answer:
a = 15 in.
b = 36 in.
A = ab/2
A = (15)(36)/2
A = 270 sq. in

b.

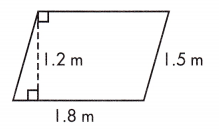
A = ____________ m²
Answer:
Given,
b = 1.8 m
h = 1.2 m
A = bh
A = 1.8 × 1.2
A = 1.16 sq. m

c.

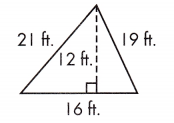
A = ____________ ft²
Answer:
Given,
b = 16 ft
h = 12 ft
A = 1/2 × bh
A = 1/2 × 16 × 12
A = 96 sq. ft

Answer the questions about the angles below. ∠M = 55°, ∠X = 35°

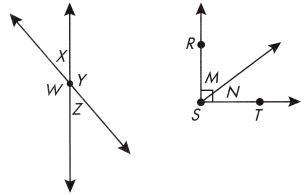
Question 21.
∠Y = ______________
Answer:
∠X = 35°
∠X + ∠Y = 180°
35° + ∠Y = 180°
∠Y = 180° – 35°
∠Y = 145°

Question 22.
∠Z = _______________
Answer:
∠X = 35°
∠Y = 145°
∠Z + ∠Y = 180°
145° + ∠Z = 180°
∠Z = 180° – 145°
∠Z = 35°

Question 23.
∠W = _______________
Answer:
∠Z = 35°
∠W + ∠Z = 180°
∠W + 35° = 180°
∠W = 180° – 35° = 145°

Question 24.
∠N = _______________
Answer:
∠M = 55°
∠M + ∠N = 90°
55° + ∠N = 90°
∠N = 90° – 55°
∠N = 35°

Find the volume of each figure. Round to the nearest hundredth.

Question 25.
a.

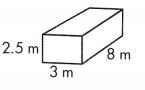
V = ___________ m³
Answer:
Given,
l = 3m
b = 8 m
h = 2.5 m
We know that,
V = lbh
V = 3 × 8 × 2.5
V = 60 cu. m

b.

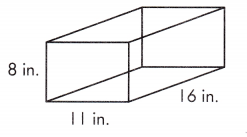
V = _____________ in.³
Answer:
Given,
l = 11 in.
w = 16 in.
h = 8 in.
We know that,
V = lbh
V = 11 × 16 × 8
V = 1408 cu. in

c.

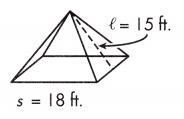
V = ______________ ft.³
Answer:
s = 18 ft
l = 15 ft
V = a² h/3
V = 18² (15)/3
V = 18 × 18 × 5
V = 1620 cu. ft

Create a free diagram using the situation described below and use it to answer the questions.

Question 26.
Tracy decides to visit the concession stand while she is at the movies. She wants a drink, popcorn, and candy. She can choose between a cola, juice, and water to drink. She can top her popcorn with butter or have it plain. Finally, she has a choice of chocolate mints, red licorice, or caramels for her candy. Make a tree diagram that shows all possible combinations.
Answer:

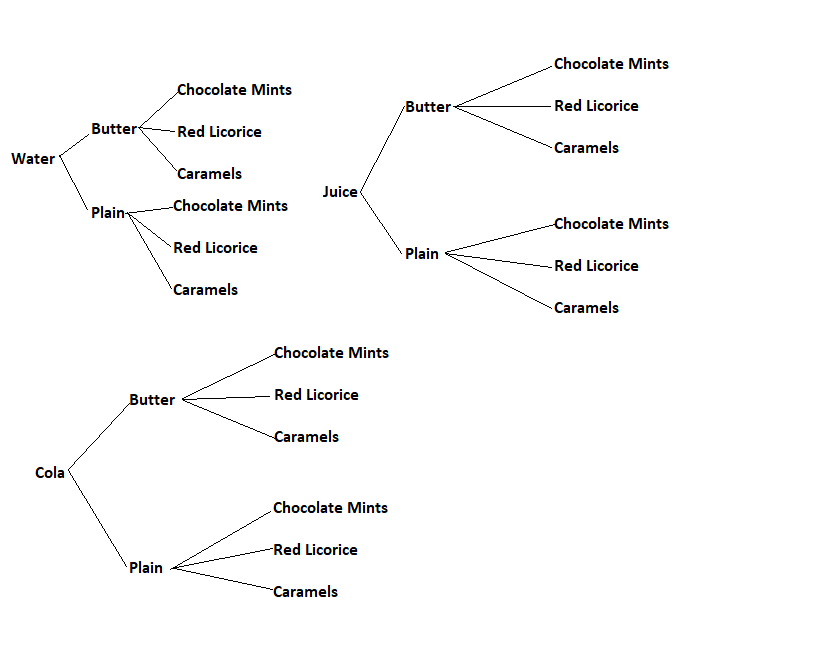
Question 27.
What is the total number of possible outcomes?
Answer:
From the above tree diagram we can say that the total number of possible outcomes are 18.

Question 28.
What is probability of having red licorice?
Answer:
Total number of possible outcomes is 18.
Red licorice = 6/18 = 1/3

Question 29.
What is the probability of having buttered popcorn and caramels?
Answer:
The probability of having buttered popcorn and caramels
= 3/18 = 1/6

Complete the items below.

Sample quiz scores are collected from two classes.

Question 30.
Create a graphic display for both sets of quiz scores.
Answer:

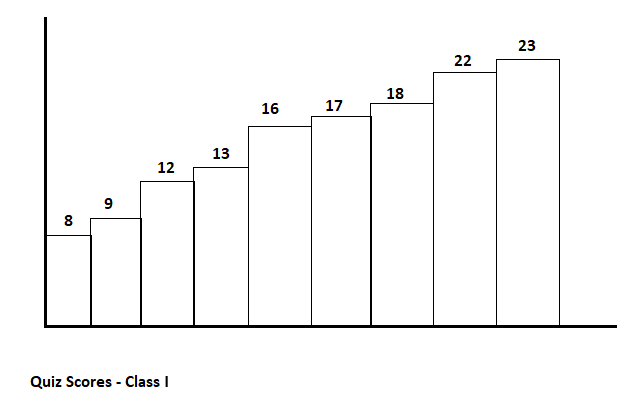
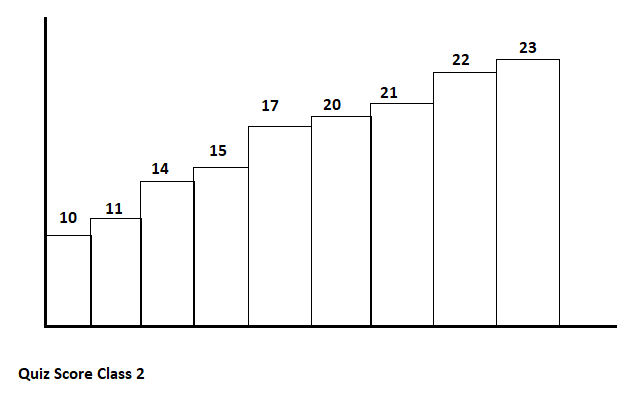
Question 31.
Find the measures of center and the range for both sets of quiz scores.
median: ______________
mode: ______________
mean: ______________
range: ______________

median: ______________
mode: ______________
mean: ______________
range: ______________
Answer:
Quiz Score Class 1:
Given data,
8, 9, 12, 13, 16, 17, 18, 22, 23
Mean = (8 + 9 + 12 + 13 + 16 + 17 + 18 + 22 + 23)/9
Mean = 15.33
8, 9, 12, 13, 16, 17, 18, 22, 23
Median = 16
Mode = 8, 9, 12, 13, 16, 17, 18, 22, 23
Range = 23 – 8
Range = 15

Quiz Score Class 2:
Given data,
10, 11, 14, 15, 17, 20, 21, 22, 23
Mean = (10 + 11 + 14 + 15 + 17 + 20 + 21 + 22 + 23)/9
Mean = 17
Median = 17
Mode = 10, 11, 14, 15, 17, 20, 21, 22, 23
Range = 23 – 10 = 13

Question 32.
If there are 30 students in Class 1, what is the best prediction for the number of students who scored a 10 or less on the quiz?
Answer: 9 students scored 10 or less on the quiz

Question 33.
If there are 25 students in Class 2, what is the best prediction for the number of students who scored more than 20 on the quiz?
Answer: 10 students scored more than 20 on the quiz

Question 34.
Tell one way the two data sets are alike and different.
alike: _____________
different: ______________
Answer:
The number of observations in two data sets are alike.
The mean, median, mode and range are different in two data sets.

Tell which property is used in each equation (commutative, associative, or identity).

Question 35.
a. 5 + 3 = 3 + 5 _____________
Answer:
Commutative Property of Addition
The commutative property of addition says that changing the order of addends does not change the sum.

b. 0 + 8 = 8 _______________
Answer:
Identity Property of Addition
The sum of 0 and any number is that number.

Question 36.
a. (2 + 1) + 5 = 2 + (1 + 5) _______________
Answer:
Associative Property of Addition
Associative Property of Addition states that changing the grouping of addends does not change the sum.

b. -5 + 5 = 0 _______________
Answer:
The inverse property of addition states that adding a number and its opposite, called the additive inverse, will produce a sum of zero.