Spectrum Math Grade 7 Chapter 5 Pretest Answer Key

This handy Spectrum Math Grade 7 Answer Key Chapter 5 Pretest provides detailed answers for the workbook questions

Spectrum Math Grade 7 Chapter 5 Pretest Answers Key

Check What You Know

Find the area of each figure.

Question 1.
a.

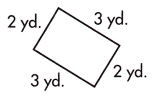
____________ square yards
Answer:
6 square yards.

Explanation:
Area of a rectangle = Length x Width
A = 3 x 2 = 6
Area = 6 square yards.
b.

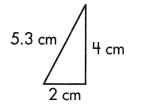
____________ square centimeters
Answer:
4 square centimeters.

Explanation:
Area of a Triangle = (1/2) [ Base x Height]
A = (1/2) 4 x 2
A = 2 x 2
A = 4 sq cm

c.

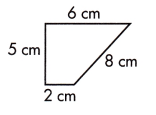
____________ square centimeters.
Answer:
20 square centimeters.

Explanation:
Area of a rectangle of length L = 6 cm and width 5 cm.
A1 = length  x width
A1 = 6 x 5
A1 = 30 sq cm.
Area of triangle of Base 4 cm and height 5 cm.
A2 = (1/2) base x height
A2 = (1/2) x 4 x 5
A2 = 2 x 5
A2 = 10 sq cm.
Area of a given figure is A = A1 – A2
A = 30 – 10
A = 20 square centimeters.

Find the circumference and area of each circle. Use 3.14 for π.

Question 2.
a.

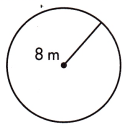
A = ____________ square meters
C = ____________ meters
Answer:
A = 200.96 square meters
C = 50.24 meters
Explanation:
Given that,
Radius = 8 m
Diameter = 2r
D = 2 x 8
D = 16 cm.
We know that,
π = 3.14 or 22/7
A = π × r²
A = 3.14 x 8 x 8
A = 200.96 square meters.
Circumference = 2πr
C = 2 x 3.14 x 8
C = 50.24 meters.

b.

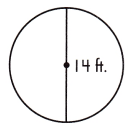
A = ____________ square feet
C = ____________ feet
Answer:
A = 153.86 square feet
C = 43.96 feet

Explanation:
Given,
Diameter = 14 ft
Radius = d/2
r = 14/2
r = 7 ft
We know that,
π = 3.14 or 22/7
A = π × r²
A = 3.14 x 7 x 7
A = 153.86 square feet.
Circumference = 2πr
C = 2 x 3.14 x 7
C = 43.96 feet.

c.

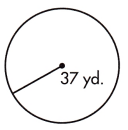
A = ____________ square yards
C = ____________ yards
Answer:
A = 4,298.66 square yards
C = 232.36 yards

Explanation:
Given,
Radius = 37 yd
Diameter = 2r
D = 37 x 2
D = 74 yd.
We know that,
π = 3.14 or 22/7
A = π × r²
A = 3.14 x 37 x 37
A = 4,298.66 square yards
Circumference = 2πr
C = 2 x 3.14 x 37
C = 232.36 yards.

Find the length of the missing side for the pair of similar triangles.

Question 3.

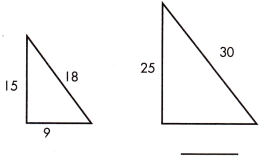
Answer:
missing side length is 15.

Explanation:

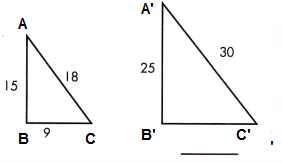
\(\frac{AB}{A’B’}\) = \(\frac{BC}{B’C’}\)
\(\frac{15}{25}\) = \(\frac{9}{B’C’}\) Use a proportion.
15 × BC = 25 × 9
BC = \(\frac{25 × 9}{15}\)
BC = 5 x 3
BC = 15.

Write ratios to determine if the sides are proportional. Then, write similar or not similar.

Question 4.

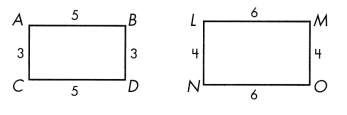
Answer:
not similar.

Explanation:
Two parallelogram  are not similar if their corresponding angles are not congruent and the lengths of their corresponding sides are not proportional.
\(\frac{AB}{LM} \) = \(\frac{5}{6} \)
\(\frac{BD}{MO} \) = \(\frac{3}{4} \)
\(\frac{DC}{ON} \)= \(\frac{5}{6} \)
\(\frac{CA}{NL} \)= \(\frac{3}{4} \)
Therefor the angle measures are not congruent.

Use the angles and side lengths given to create a triangle. Label the measurements on your drawing.

Question 5.
Angles: 60° and 100°
Side: 2 inches
Answer:

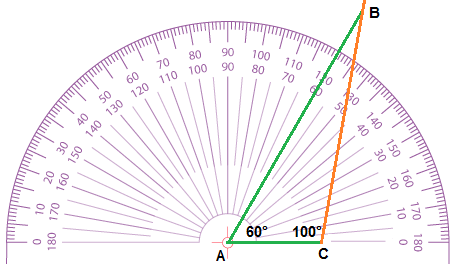
Explanation:
Step 1: Use a ruler to draw a line that is 2 in.
Step 2: Use a protractor to draw a line that creates the desired angle with the first line (60°).
Step 3: Use the protractor to measure the 2^nd known angle 100°from the other end of your original line.
Step 4: Label the triangle.

Will the following measurements make a triangle? Circle yes or no.

Question 6.
5 meters, 9 meters, 20 meters
yes
no
Answer:

Explanation:
Given a = 5, b = 9, c = 20
a + b > c
a + c > b
b + c > a
5 + 9 is not greater then 20
9 + 20 is greater then 5
Because the measurements do not follow the rules, the side lengths can not make a triangle.

Find the volume of each figure.

Question 7.
a.

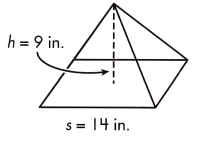
V = _____________ in.³
Answer:
V = 588 in.³

Explanation:
V = \(\frac{1}{3}\)s²h
Given,
s = 14 in, h = 9 in
V = \(\frac{1}{3}\) 14² × 9
V = \(\frac{1764}{3}\)
V = 588 in³

b.

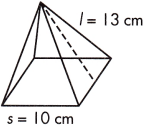
V = _____________ cm³
Answer:
V = 400 cm.³

Explanation:
V = \(\frac{1}{3}\)s2h
Given,
s = 10 cm, l = 13 cm
According to the Pythagorean Theorem to find the height,
a = \(\frac{1}{2}\) of the side length,
a = \(\frac{1}{2}\) x 10
a = \(\frac{10}{2}\)  = 5 in.
b = the height of the pyramid, c = length (26 in)
a² + b² = c²
5² + b² = 13²
25 + b² = 169
b² = 169 – 25
b² = 144
b = 12 in
V = \(\frac{1}{3}\) 10² × 12
V = \(\frac{1200}{3}\)
V = 400 in³

c.

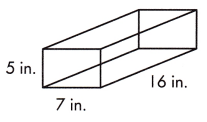
V = _____________ in.³
Answer:
V = 560 in.³

Explanation:
V = l × w × h.
l = 16 in, w = 7 in and h = 5 in,
V = 16 × 7 × 5
V = 560 in³

Tell what shape is created by each cross section.

Question 8.

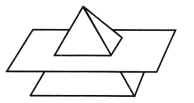
Answer:
Square.

Explanation:
We know that,
A cross section of a 3-dimensional figure is the place where a plane cuts through the figure. The shape and size of the cross section depends on where the plane slices the figure.
When the plane intersects a triangular prism square is created.

Question 9.

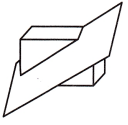
Answer:
Quadrilateral.

Explanation:
We know that,
A cross section of a 3-dimensional figure is the place where a plane cuts through the figure. The shape and size of the cross section depends on where the plane slices the figure.
When the plane intersects a rectangular prism at an angle, it will create a quadrilateral, but not necessarily a rectangle.

Use the figure below to answer the questions.

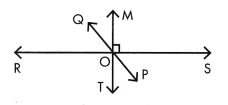
Question 10.
Name an angle complementary to angle
SOP. ___________
Answer:
∠POT

Explanation:
If two angles add up to 90 degrees then they are known as complementary angles.
∠POT is a complementary angle.

Question 11.
Name an angle supplementary to angle
MOQ. ____________
Answer:
∠MOP or  ∠QOT

Explanation:
If two angles add up to 180 degrees then they are known as supplementary.
∠MOP or  ∠QOT are supplementary angles.

Solve each problem.

Question 12.
A scale drawing of a car is 3 inches to 12 inches. If the car is 48 inches high, how high is the drawing?
The drawing is _______________________ inches high.
Answer:
12 inches high.

Explanation:
A scale drawing of a car is 3 inches to 12 inches.
If the car is 48 inches high.
The height of the drawing = 12 x 3 = 48 inches.

Question 13.
On a map, each inch represents 25 miles. What is the length of a highway if it is 6 inches long on a map?
The highway is _____________________ miles long.
Answer:
150 miles long.

Explanation:
On a map, each inch represents 25 miles.
If is the length of a highway is 6 inches long on a map then the highway is,
1 inch = 25 miles
6 inches = 6 x 25 = 150 miles long.

Question 14.
Adam needs to wrap a package that is 11 inches long, 8.5 inches wide, and 6 inches high. What is the volume of the package?
The package’s volume is ______________________ cubic inches.
Answer:
561 cubic inches.

Explanation:
Adam needs to wrap a package that is 11 inches long, 8.5 inches wide, and 6 inches high.
V = lbh.
The volume of the package, 11 x 8.5 x 6 = 561 cubic inches.