Spectrum Math Grade 7 Chapter 5 Lesson 7 Answer Key Angle Relationships

This handy Spectrum Math Grade 7 Answer Key Chapter 5 Lesson 5.7 Angle Relationships provides detailed answers for the workbook questions

Spectrum Math Grade 7 Chapter 5 Lesson 5.7 Angle Relationships Answers Key

When two lines intersect, they form angles that have special relationships.
Vertical angles are opposite angles that have the same measure.
Supplementary angles are two angles whose measures have a sum of 180°.
Complementary angles are two angles whose measures have a sum of 90°.
A bisector divides an angle into two angles of equal measure.

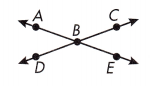
∠ABC and ∠DBE are vertical.
∠ABD and ∠DBE are supplementary.

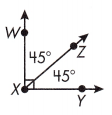
∠WXZ and ∠ZXY are complementary.
\(\overrightarrow{X Z}\) the bisector of ∠WXY.

Identify each pair of angles as supplementary or vertical.

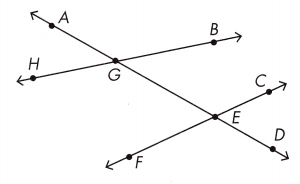
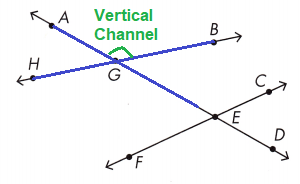
Question 1.
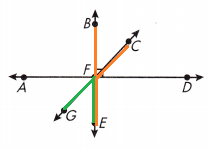
∠AGB and ∠HGE _______________
Answer:
Vertical.

Explanation:

When two lines intersect, they form angles that have special relationships.
Vertical angles are opposite angles that have the same measure.

Question 2.
∠BGE and ∠HGE ______________
Answer:
Supplementary.

Explanation:
Supplementary angles are two angles whose measures have a sum of 180°.

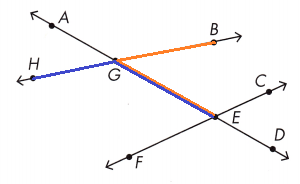
∠BGE and ∠HGE are supplementary angles.

Question 3.
∠GEC and ∠CED ______________
Answer:
Supplementary.

Explanation:
Supplementary angles are two angles whose measures have a sum of 180°.
∠GEC and ∠CED are supplementary angles.

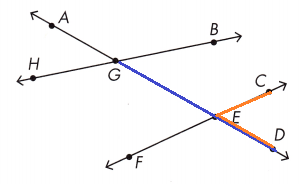
Question 4.
∠GEC and ∠DEF ______________
Answer:
Vertical.

Explanation:
When two lines intersect, they form angles that have special relationships.
∠GEC and ∠DEF Vertical angles are opposite angles that have the same measure.

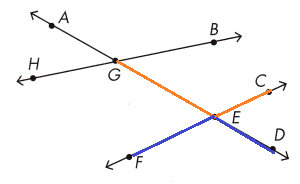
Question 5.
∠AGH and ∠BGE ______________
Answer:
Vertical.

Explanation:
When two lines intersect, they form angles that have special relationships.
∠AGH and ∠BGE Vertical angles are opposite angles that have the same measure.

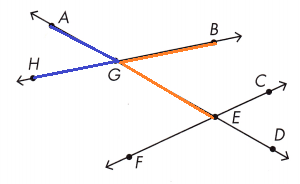
Question 6.
∠GEF and ∠DEF ______________
Answer:
Supplementary.

Explanation:
Supplementary angles are two angles whose measures have a sum of 180°.
∠GEF and ∠DEF are supplementary angles.

Solve each problem.

Question 7.
∠A and ∠G are vertical angles. The measure of ∠A is 72°. What is the measure of ∠G?
Answer:
72°

Explanation:

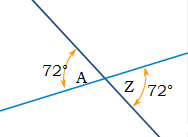
When two lines intersect, they form angles that have special relationships.
Vertical angles are opposite angles that have the same measure.
∠A and ∠G are vertical angles. The measure of ∠A is 72°, then the measure of ∠G is also 72°.

Question 8.
∠Y and ∠Z are supplementary angles. The measure of ∠Y is 112°. What is the measure of ∠Z?
Answer:
68°

Explanation:

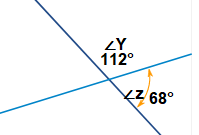
Supplementary angles are two angles whose measures have a sum of 180°.
∠Y and ∠Z are supplementary angles.
∠Z = 180° – ∠Y
∠Z = 180° – 112°
∠Z  = 68°

Question 9.
∠A and ∠B are complementary angles. The measure of ∠A is 53°. What is the measure of ∠B?
Answer:
37°

Explanation:

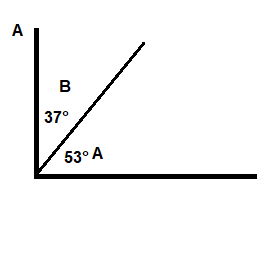
Complementary angles are two angles whose measures have a sum of 90°.
∠A and ∠B are complementary angles.
∠B = 90 – ∠A
∠B = 90° – 53°
∠B  = 37°

Question 10.
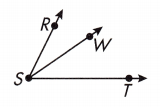
∠RST is bisected by ray SW. The measure of ∠WST is 30°, what is the measure of ∠RST?

Answer:
60°

Explanation:
The bisector is a line that divides a line or an angle into two equivalent parts.
The bisector of a segment always contains the midpoint of the segment.
∠RST is bisected by ray SW
∠RSW and ∠WST are two angles.
∠RST = 2 x ∠WST
∠RST = 2 x 30°

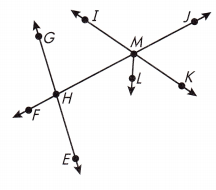
Use the figure at the right to answer questions 1-6.

Question 1.
Name an angle that is vertical to ∠EHF.
Answer:
∠GHJ or ∠GHM

Explanation:

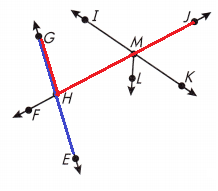
As shown in the above figure ∠GHJ or ∠GHM are angles is vertical to ∠EHF.
We know that,
Vertical angles are opposite angles that have the same measure.

Question 2.
Name an angle that is vertical to ∠EHM.
Answer:
∠FHG

Explanation:

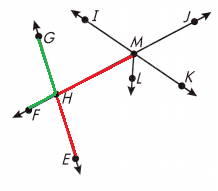
We know that,
Vertical angles are opposite angles that have the same measure.
As shown in the above figure ∠FHG angle is vertical to ∠EHF.

Question 3.
Name an angle that is supplementary to ∠IMJ.
Answer:
∠JMK or ∠IMH

Explanation:

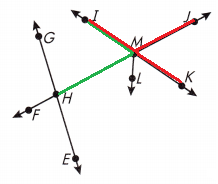
We know that,
Supplementary angles are two angles whose measures have a sum of 180°.
As shown in the above figure ∠JMK or ∠IMH an angle that is supplementary to ∠IMJ.

Question 4.
Name the bisector of ∠HMK.
Answer:
\(\overrightarrow{ML}\)

Explanation:

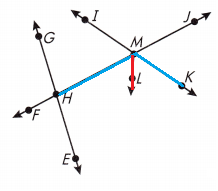
The bisector is a line that divides a line or an angle into two equivalent parts.
The bisector of a segment always contains the midpoint of the segment.
As shown in the above figure the bisector of ∠HMK is \(\overrightarrow{ML}\)

Question 5.
Name an angle that is vertical to ∠JMK.
Answer:
∠IMH

Explanation:

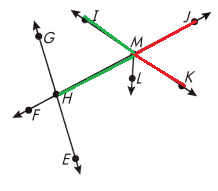
We know that,
Vertical angles are opposite angles that have the same measure.
As shown in the above figure the  ∠IMH an angle that is vertical to ∠JMK.

Question 6.
Name an angle that is supplementary to ∠JMK.
Answer:
∠IMJ or ∠KMH

Explanation:

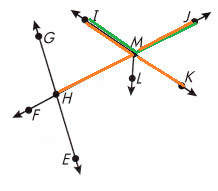
We know that,
Supplementary angles are two angles whose measures have a sum of 180°.
As shown in the above figure ∠IMJ or ∠KMH is an angle that is supplementary to ∠JMK

Use the figure at the right to answer questions 7-10

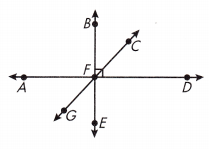
Question 7.
Name an angle complementary to ∠BFC.
Answer:
∠CFD

Explanation:

We know that,
Complementary angles are two angles whose measures have a sum of 90°.
As shown in the above figure ∠CFD  angle complementary to ∠BFC.

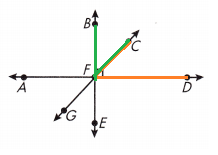
Question 8.
Name an angle complementary to ∠AFG.
Answer:
∠GFE

Explanation:

We know that,
Complementary angles are two angles whose measures have a sum of 90°.
As shown in the above figure ∠GFE angle complementary to ∠AFG.

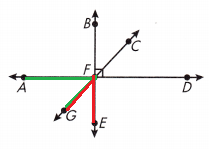
Question 9.
Name an angle that is supplementary to ∠CFD.
Answer:
∠AFC or ∠DFG

Explanation:

We know that,
Supplementary angles are two angles whose measures have a sum of 180°.
As shown in the above figure ∠AFC or ∠DFG an angle that is supplementary to ∠CFD

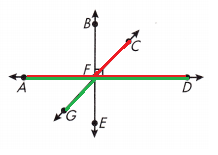
Question 10.
Name an angle that is supplementary to ∠GFE.
Answer:
∠CFE or ∠GFB

Explanation:

We know that,
Supplementary angles are two angles whose measures have a sum of 180°.
As shown in the above figure ∠CFE or ∠GFB an angle that is supplementary to ∠GFE

Solve.

Question 11.
∠RST is supplementary to angle ∠PSO. The measure of ∠RST is 103°. What is the measure of ∠PSO?
Answer:
77°

Explanation:
Supplementary angles are two angles whose measures have a sum of 180°.
So, ∠RST and ∠PSO are supplementary angles.
∠PSO = 180° – ∠RST
∠PSO = 180° – 103°
∠PSO = 77°

Question 12.
∠MNO and ∠NOP are complementary. The measure of ∠NOP is 22°. What is the measure of ∠MNO?
Answer:
68°

Explanation:
We know that,
Complementary angles are two angles whose measures have a sum of 90°.
So, ∠MNO and ∠NOP are complementary angles.
∠MNO = 90° – ∠NOP
∠PSO = 90° – 22°
∠PSO = 68°

Question 13.
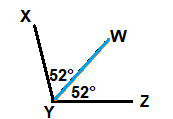
∠XYZ is bisected by \(\overrightarrow{Y W}\). The measure of ∠XYW is 52°. What is the measure of ∠WYZ? What is the measure of ∠XYZ?
The measure of ∠WYZ is _____________. The measure of ∠XYZ is _______________.
Answer:
52°, 104°

Explanation:

The bisector is a line that divides a line or an angle into two equivalent parts.
The bisector of a segment always contains the midpoint of the segment.
The measure of ∠XYW is 52°, then ∠WYZ is also  52°, as ∠XYZ is bisected by \(\overrightarrow{Y W}\).
The measure of ∠XYZ = sum of The measure of ∠XYW and ∠WYZ.
∠XYZ = 52° + 52°
∠XYZ = 104°

Question 14.
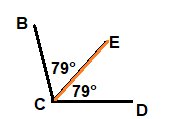
∠BCD is bisected by \(\overrightarrow{C E}\). The measure of ∠DCE is 79°.
What is the measure of ∠BCF? What is the measure of ∠BCD? The measure of ∠BCE is ______________. The measure of ∠BCD is _____________.
Answer:
79°, 158°

Explanation:

The bisector is a line that divides a line or an angle into two equivalent parts.
The bisector of a segment always contains the midpoint of the segment.
The measure of ∠DCE is 79°, then ∠BCE is also  79°, as ∠BCD is bisected by \(\overrightarrow{CE}\).
The measure of ∠BCD = sum of The measure of ∠BCE and ∠BCE.
∠XYZ = 79° + 79°
∠XYZ = 158°

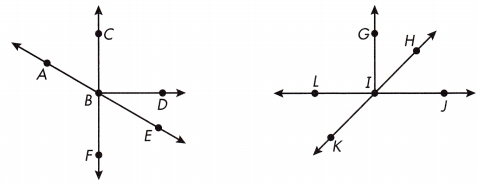
Use 3 letters to name each angle in the figures below.

Question 1.
Which pair of angles are complementary?

Answer:
∠FBE / ∠EBD, ∠GIH / ∠HIJ

Explanation:

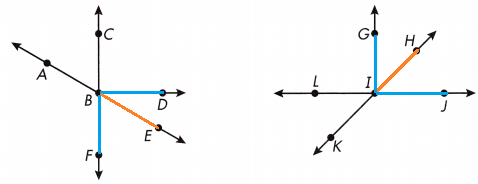
We know that,
Complementary angles are two angles whose measures have a sum of 90°.
As shown in the above figure, ∠FBE / ∠EBD, ∠GIH / ∠HIJ pair of angles are complementary.

Question 2.
Which pairs of angles are supplementary?

Answer:
∠ABC / ∠CBE, ∠CBD / ∠DBF, ∠CBE / ∠EBF, ∠EBF / ∠FBA, ∠FBA / ∠ABC, ∠LIK / ∠LIH
∠LIK / ∠KIJ, ∠LIG / ∠GIJ, ∠LIH / ∠HIJ, ∠HIJ / ∠JIK

Explanation:

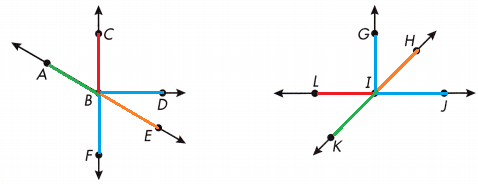
We know that,
Supplementary angles are two angles whose measures have a sum of 180°.
So, all pairs of angles are supplementary in the above figure are listed below,
∠ABC / ∠CBE, ∠CBD / ∠DBF, ∠CBE / ∠EBF, ∠EBF / ∠FBA, ∠FBA / ∠ABC, ∠LIK / ∠LIH
∠LIK / ∠KIJ, ∠LIG / ∠GIJ, ∠LIH / ∠HIJ, ∠HIJ / ∠JIK

Question 3.
Which pairs of angles are vertical angles?

Answer:
∠ABC / ∠FBE, ∠CBE / ∠FBA, ∠KIL / ∠HIJ, ∠LIH / ∠KIJ

Explanation:

We know that,
Vertical angles are opposite angles that have the same measure.
So, all pairs of angles are vertical angles in the above figure are listed below,
∠ABC / ∠FBE, ∠CBE / ∠FBA, ∠KIL / ∠HIJ, ∠LIH / ∠KIJ

Question 4.
Name a point on an angle bisector.
Answer:
H

Explanation.

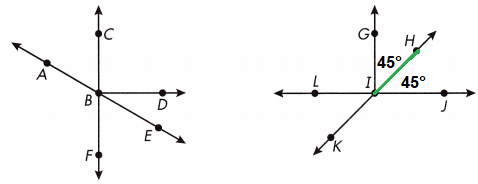
The bisector is a line that divides a line or an angle into two equivalent parts.
The bisector of a segment always contains the midpoint of the segment.
So, ∠GIH and ∠HIJ are complementary.
\(\overrightarrow{IH}\) the bisector of ∠GIJ.

Question 5.
Which angle does the angle bisector named in question 4 bisect?
Answer:
Answer will vary.

Explanation.

∠GIH and ∠HIJ are complementary.
\(\overrightarrow{IH}\) the bisector of ∠GIJ.
The measure of ∠GIJ = sum of The measure of ∠GIH and ∠HIJ.
∠GIJ = 45° + 45°
∠GIJ = 90°

Mark the right angles on the figures above. Then, solve each problem.

Question 6.
If ∠DBE measures 39°, what does ∠FBE measure?
Answer:
51°

Explanation:
Complementary angles are two angles whose measures have a sum of 90°.
∠DBE and ∠FBE are complementary angles.
∠FBE = 90 – ∠DBE
∠FBE = 90° – 39°
∠FBE  = 51°

Question 7.
If ∠HIJ measures 45°, what does ∠KIJ measure?
Answer:
135°

Explanation:

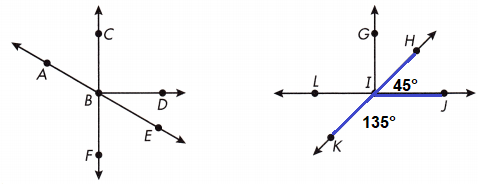
Supplementary angles are two angles whose measures have a sum of 180°.
∠HIJ and ∠KIJ are supplementary angles.
∠KIJ = 180° – ∠HIJ
∠KIJ = 180° – 45°
∠KIJ = 135°

Question 8.
If ∠LIH measures 135°, what does ∠KIJ measure?
Answer:
135°

Explanation:

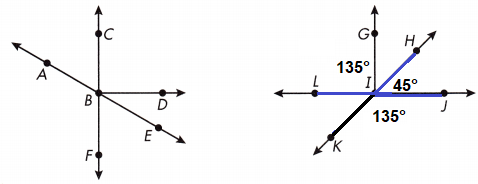
A pair of vertically opposite angles are always equal to each other.
Also, a vertical angle and its adjacent angle are supplementary angles.
∠LIH and ∠KIJ are equal angles.
∠KIJ = ∠LIH
∠KIJ = 135°

Question 9.
If ∠CBE measures 131°, what does ∠DBE measure?
Answer:
41°

Explanation:

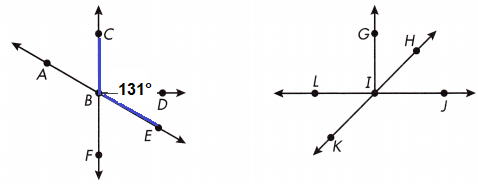
∠DBE = ∠CBE – ∠CBD
∠DBE = 131° – 90°
∠DBE = 41°

Question 10.
If ∠ABD measures 149°, what does ∠ABC measure?
Answer:
59°

Explanation:

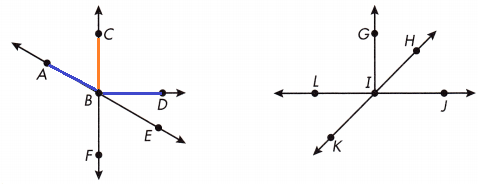
∠ABC = ∠ABD – ∠CBD
∠ABC = 149° – 90°
∠ABC = 59°