Practice with the help of Spectrum Math Grade 5 Answer Key Chapters 1-10 Final Test regularly and improve your accuracy in solving questions.
Spectrum Math Grade 5 Chapters 1-10 Final Test Answers Key
Add, subtract, multiply, or divide.
Question 1.
a.
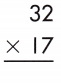
Answer: 544
Follow the below steps to multiply two numbers:
- Multiply by the number in the ones place.
- Put a zero below in the ones place.
- Multiply by the number in the tens place.
- Add them up.
32
x 17
———
224
+ 320
———–
544
———–
b.
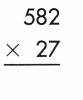
Answer: 15714
Follow the below steps to multiply two numbers:
- Multiply by the number in the ones place.
- Put a zero below in the ones place.
- Multiply by the number in the tens place.
- Add them up.
582
x 27
———
4074
+ 11640
———–
15714
———–
c.
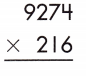
Answer: 2003184
Follow the below steps to multiply two numbers:
- Multiply by the number in the ones place.
- Put a zero below in the ones place.
- Multiply by the number in the tens place.
- Add them up.
9274
x 216
———
55644
92740
+185840
———–
2003184
———–
d.
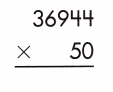
Answer: 1747200
Follow the below steps to multiply two numbers:
- Multiply by the number in the ones place.
- Put a zero below in the ones place.
- Multiply by the number in the tens place.
- Add them up.
34944
x 50
———
00000
+174720
———–
1747200
———–
Question 2.
a.
![]()
Answer: 134 r2

The quotient is 134
The remainder is 2
b.
![]()
Answer: 1398 r18
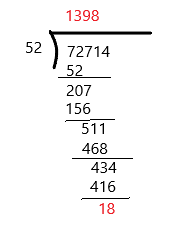
The quotient is 1398
The remainder is 18
c.
![]()
Answer: 58
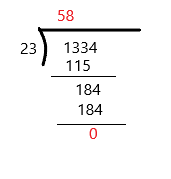
The quotient is 58
The remainder is 0
d.
![]()
Answer: 93
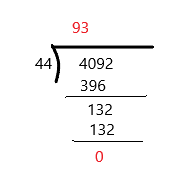
The quotient is 93
The remainder is 0
Question 3.
a.
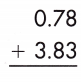
Answer: 4.61

To add decimals to hundredths, line up the decimal points. Then, perform addition normally.
b.
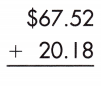
Answer: 87.70

To add decimals to hundredths, line up the decimal points. Then, perform addition normally.
c.
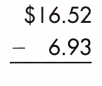
Answer: 9.59

To subtract decimals to hundredths, line up the decimal points. Then, perform subtraction normally.
d.
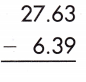
Answer: 21.24

To subtract decimals to hundredths, line up the decimal points. Then, perform subtraction normally.
Question 4.
a.
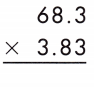
Answer: 261.589

When multiplying decimals, count the number of decimal places in each factor to figure out the placement of the decimal point in the product.
There are 1 decimal place in first factor and 2 decimal places in second factor, so there should be 3 decimal places in the product.
b.
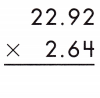
Answer: 60.5088

When multiplying decimals, count the number of decimal places in each factor to figure out the placement of the decimal point in the product.
There are 2 decimal places in first factor and 2 decimal places in second factor, so there should be 4 decimal places in the product.
c.

Answer: 7186.7528

When multiplying decimals, count the number of decimal places in each factor to figure out the placement of the decimal point in the product.
There are 2 decimal places in first factor and 2 decimal places in second factor, so there should be 4 decimal places in the product.
d.
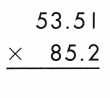
Answer: 4559.052

When multiplying decimals, count the number of decimal places in each factor to figure out the placement of the decimal point in the product.
There are 2 decimal places in first factor and 1 decimal place in second factor, so there should be 3 decimal places in the product.
Question 5.
a.
![]()
Answer: 76
38.76 ÷ 0.51
To make the divisor into a whole number, move the decimal point in the divisor and the dividend the same number of places to the right. And, then perform the division normally.
So, the above division becomes 3876 ÷ 51
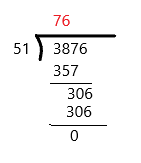
Therefore, the answer is 76
b.
![]()
Answer: 8.2
64.78 ÷ 7.9
To make the divisor into a whole number, move the decimal point in the divisor and the dividend the same number of places to the right. And, then perform the division normally.
So, the above division becomes 6478 ÷ 790
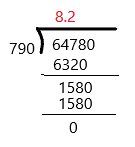
Therefore, the answer is 8.2
c.
![]()
Answer: 3.2
22.816 ÷ 7.13
To make the divisor into a whole number, move the decimal point in the divisor and the dividend the same number of places to the right. And, then perform the division normally.
So, the above division becomes 22816 ÷ 7130
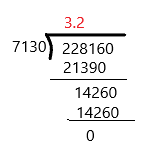
Therefore, the answer is 3.2
d.
![]()
Answer: 4.3
39.99÷ 9.3
To make the divisor into a whole number, move the decimal point in the divisor and the dividend the same number of places to the right. And, then perform the division normally.
So, the above division becomes 3999 ÷ 930
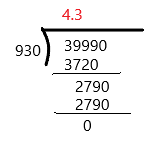
Therefore, the answer is 4.3
Add, subtract, multiply or divide. Write answers in simplest form.
Question 6.
a.
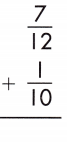
Answer: \(\frac{41}{60}\)
\(\frac{7}{12}\) + \(\frac{1}{10}\)
To add or subtract fractions, the denominators must be the same.
When you have unlike denominators, find the least common multiple (LCM) and rename the fractions.
In the given question, the denominators are 12 and 10, so the LCM of 12 and 10 should be find out using their multiples
Multiples of 12: 12,24,36,48,60,72
Multiples of 10: 10,20,30,40,50,60,70
So, The LCM of 12 and 10 is 60.
To change each fraction so it has the same denominator, multiply both the numerator and denominator by the same number.
=\(\frac{7}{12}\) × \(\frac{5}{5}\) + \(\frac{1}{10}\) × \(\frac{6}{6}\)
=\(\frac{7 × 5}{12 × 5}\) + \(\frac{1 × 6}{10 ×6}\)
=\(\frac{35}{60}\) + \(\frac{6}{60}\)
=\(\frac{35 + 6}{60}\)
= \(\frac{41}{60}\)
Therefore, \(\frac{7}{12}\) + \(\frac{1}{10}\) = \(\frac{41}{60}\)
b.
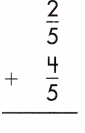
Answer: \(\frac{6}{5}\)
\(\frac{2}{5}\) + \(\frac{4}{5}\)
Denominators are called common when they share the same number.
To add or subtract fractions with like denominators, perform the given operation on the numerators and use the common denominator.
=\(\frac{2 + 4}{5}\)
= \(\frac{6}{5}\)
Therefore, \(\frac{2}{5}\) + \(\frac{4}{5}\) = \(\frac{6}{5}\)
c.
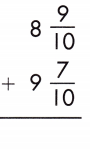
Answer: 18\(\frac{6}{10}\)
8\(\frac{9}{10}\) + 9\(\frac{7}{10}\)
Convert the mixed fraction into improper fraction
\(\frac{89}{10}\) + \(\frac{97}{10}\)
Denominators are called common when they share the same number.
To add or subtract fractions with like denominators, perform the given operation on the numerators and use the common denominator.
=\(\frac{89 + 97}{10}\)
= \(\frac{186}{10}\)
=18\(\frac{6}{10}\)
Therefore, 8\(\frac{9}{10}\) + 9\(\frac{7}{10}\) = 18\(\frac{6}{10}\)
d.
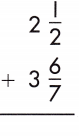
Answer: 6\(\frac{5}{14}\)
2\(\frac{1}{2}\) + 3\(\frac{6}{7}\)
Convert the mixed fraction into improper fraction
\(\frac{5}{2}\) + \(\frac{27}{7}\)
To add or subtract fractions, the denominators must be the same.
When you have unlike denominators, find the least common multiple (LCM) and rename the fractions.
In the given question, the denominators are 2 and 7, so the LCM of 2 and 7 should be find out using their multiples
Multiples of 2: 2,4,6,8,10,12,14,16
Multiples of 7: 7,14,21
So, The LCM of 2 and 7 is 14.
To change each fraction so it has the same denominator, multiply both the numerator and denominator by the same number.
=\(\frac{5}{2}\) × \(\frac{7}{7}\) + \(\frac{27}{7}\) × \(\frac{2}{2}\)
=\(\frac{5 × 7}{2 × 7}\) + \(\frac{27 × 2}{7 ×2}\)
=\(\frac{35}{14}\) + \(\frac{54}{14}\)
=\(\frac{35 + 54}{14}\)
= \(\frac{89}{14}\)
= 6\(\frac{5}{14}\)
Therefore, 2\(\frac{1}{2}\) + 3\(\frac{6}{7}\) = 6\(\frac{5}{14}\)
Question 7.
a.

Answer: \(\frac{1}{2}\)
\(\frac{5}{8}\) – \(\frac{1}{8}\)
Denominators are called common when they share the same number.
To add or subtract fractions with like denominators, perform the given operation on the numerators and use the common denominator.
=\(\frac{5-1}{8}\)
= \(\frac{4}{8}\)
=\(\frac{1}{2}\)
Therefore, \(\frac{5}{8}\) – \(\frac{1}{8}\) = \(\frac{1}{2}\)
b.
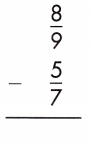
Answer: \(\frac{101}{63}\)
\(\frac{8}{9}\) – \(\frac{5}{7}\)
To add or subtract fractions, the denominators must be the same.
When you have unlike denominators, find the least common multiple (LCM) and rename the fractions.
In the given question, the denominators are 9 and 7, so the LCM of 9 and 7 should be find out using their multiples
Multiples of 9: 9,18,27,36,45,54,63,72
Multiples of 7: 7,14,21,28,35,42,49,56,63,70
So, The LCM of 9 and 7 is 63.
To change each fraction so it has the same denominator, multiply both the numerator and denominator by the same number.
=\(\frac{8}{9}\) × \(\frac{7}{7}\) – \(\frac{5}{7}\) × \(\frac{9}{9}\)
=\(\frac{8 × 7}{9 × 7}\) + \(\frac{5 × 9}{7 × 9}\)
=\(\frac{56}{63}\) + \(\frac{45}{63}\)
=\(\frac{56 + 45}{63}\)
= \(\frac{101}{63}\)
Therefore, \(\frac{8}{9}\) – \(\frac{5}{7}\) = \(\frac{101}{63}\)
c.
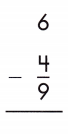
Answer:
\(\frac{6}{1}\) – \(\frac{4}{9}\)
To add or subtract fractions, the denominators must be the same.
When you have unlike denominators, find the least common multiple (LCM) and rename the fractions.
In the given question, the denominators are 1 and 9, so the LCM of 1 and 9 should be find out using their multiples
Multiples of 1: 1,2,3,4,5,6,7,8,9,10
Multiples of 9: 9,18
So, The LCM of 1 and 9 is 9.
To change each fraction so it has the same denominator, multiply both the numerator and denominator by the same number.
=\(\frac{6}{1}\) × \(\frac{9}{9}\) – \(\frac{4}{9}\) × \(\frac{1}{1}\)
=\(\frac{6 × 9}{1 × 9}\) + \(\frac{4 × 1}{9 × 1}\)
=\(\frac{54}{9}\) + \(\frac{4}{9}\)
=\(\frac{54 + 4}{9}\)
= \(\frac{58}{9}\)
Therefore,\(\frac{6}{1}\) – \(\frac{4}{9}\) = \(\frac{58}{9}\)
Question 8.
a. \(\frac{1}{2}\) × \(\frac{4}{7}\) = ______________
Answer: \(\frac{2}{7}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
\(\frac{1}{2}\) × \(\frac{4}{7}\)
= \(\frac{1 × 4}{2 × 7}\)
= \(\frac{4}{14}\)
By simplification,
= \(\frac{2}{7}\)
Therefore, \(\frac{1}{2}\) × \(\frac{4}{7}\) = \(\frac{2}{7}\)
b. \(\frac{5}{8}\) × \(\frac{3}{5}\) = ______________
Answer: \(\frac{3}{8}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
\(\frac{5}{8}\) × \(\frac{3}{5}\)
= \(\frac{5 × 3}{8 × 5}\)
= \(\frac{15}{40}\)
By simplification,
= \(\frac{3}{8}\)
Therefore, \(\frac{5}{8}\) × \(\frac{3}{5}\) = \(\frac{3}{8}\)
c. \(\frac{7}{12}\) × \(\frac{3}{8}\) = ______________
Answer: \(\frac{7}{32}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
\(\frac{7}{12}\) × \(\frac{3}{8}\)
= \(\frac{7 × 3}{12 × 8}\)
= \(\frac{21}{96}\)
By simplification,
= \(\frac{7}{32}\)
Therefore, \(\frac{7}{12}\) × \(\frac{3}{8}\) = \(\frac{7}{32}\)
d. \(\frac{9}{10}\) × \(\frac{10}{11}\) = ______________
Answer: \(\frac{9}{11}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
\(\frac{9}{10}\) × \(\frac{10}{11}\)
= \(\frac{9 × 10}{10 × 11}\)
= \(\frac{90}{110}\)
By simplification,
= \(\frac{9}{11}\)
Therefore, \(\frac{9}{10}\) × \(\frac{10}{11}\) =\(\frac{9}{11}\)
Question 9.
a. \(\frac{1}{2}\) ÷ 2 = ______________
Answer: \(\frac{1}{4}\)
To perform division, multiply it’s reciprocal
reciprocal of 2 = \(\frac{1}{2}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
\(\frac{1}{2}\) ÷ 2
= \(\frac{1}{2}\)× \(\frac{1}{2}\)
= \(\frac{1 × 1}{2 × 2}\)
= \(\frac{1}{4}\)
Therefore, \(\frac{1}{2}\) ÷ 2 = \(\frac{1}{4}\)
b. 5 ÷ \(\frac{1}{7}\) = _____________
Answer: 35
To perform division, multiply it’s reciprocal
reciprocal of \(\frac{1}{7}\) = 7
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
5 ÷ \(\frac{1}{7}\)
= 5 × 7
= 35
Therefore, 5 ÷ \(\frac{1}{7}\) =35
c. \(\frac{1}{9}\) ÷ 4 = ______________
Answer: \(\frac{1}{36}\)
To perform division, multiply it’s reciprocal
reciprocal of 4 = \(\frac{1}{4}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
\(\frac{1}{9}\) ÷ 4
= \(\frac{1}{9}\)× \(\frac{1}{4}\)
= \(\frac{1 × 1}{9 × 4}\)
= \(\frac{1}{36}\)
Therefore, \(\frac{1}{9}\) ÷ 4 = \(\frac{1}{36}\)
d. 3 ÷ \(\frac{1}{7}\) = _______________
Answer: 21
To perform division, multiply it’s reciprocal
reciprocal of \(\frac{1}{7}\) = 7
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
3 ÷ \(\frac{1}{7}\)
= 3× 7
= 21
Therefore, 3 ÷ \(\frac{1}{7}\) = 21
Question 10.
a. 4 × 1\(\frac{2}{3}\) = _____________
Answer: \(\frac{20}{3}\)
1\(\frac{2}{3}\) = \(\frac{5}{3}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
4 × 1\(\frac{2}{3}\)
= \(\frac{4}{1}\)× \(\frac{5}{3}\)
= \(\frac{4 × 5}{1 × 3}\)
= \(\frac{20}{3}\)
Therefore, 4 × 1\(\frac{2}{3}\) = \(\frac{20}{3}\)
b. 2\(\frac{1}{6}\) × 7\(\frac{4}{5}\) = ______________
Answer:
2\(\frac{1}{6}\) = \(\frac{13}{6}\)
7\(\frac{4}{5}\) = \(\frac{39}{5}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
2\(\frac{1}{6}\) × 7\(\frac{4}{5}\)
= \(\frac{13}{6}\)× \(\frac{39}{5}\)
= \(\frac{13× 39}{6 × 5}\)
= \(\frac{169}{10}\)
Therefore, 2\(\frac{1}{6}\) × 7\(\frac{4}{5}\) = \(\frac{169}{10}\)
c. 4\(\frac{1}{5}\) × 3 = ______________
Answer: \(\frac{63}{5}\)
4\(\frac{1}{5}\) = \(\frac{21}{5}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
4\(\frac{1}{5}\) × 3
= \(\frac{21}{5}\) × \(\frac{3}{1}\)
= \(\frac{21× 3}{5× 1}\)
= \(\frac{63}{5}\)
Therefore, 4\(\frac{1}{5}\) × 3 = \(\frac{63}{5}\)
d. 5\(\frac{1}{7}\) × 1\(\frac{5}{9}\) = ______________
Answer: 8
5\(\frac{1}{7}\)= \(\frac{36}{7}\)
1\(\frac{5}{9}\) = \(\frac{14}{9}\)
Multiply the numerators (the top numbers) together, and then multiply the denominators (the bottom numbers) together.
5\(\frac{1}{7}\) × 1\(\frac{5}{9}\)
= \(\frac{36}{7}\) × \(\frac{14}{9}\)
= \(\frac{36× 14}{7 × 9}\)
= 8
Therefore, 5\(\frac{1}{7}\) × 1\(\frac{5}{9}\)=8
Determine the place value of the underlined digit in each number.
Question 11.
a. 15.75 _____________
Answer: tenths place
The first digit after the decimal represents the tenths place.
7 in 15.75 is in tenths place.
b. 12,372 ____________
Answer: lakhs place
1 in 12,372 is in lakhs place.
Question 12.
72.05 _______________
Answer: hundredths place
5 in 72.05 is in hundredths place
b. 103,728 ______________
Answer: hundreds place
7 in 103,728 is in hundreds place
Round each number to the place of the underlined digit.
Question 13.
a. 103,467 _____________
Answer: 103,500
Look at the digit to the right of your underlined numeral. Determine if it is greater than or equal to 5. If so, you will round your underlined digit up. If the digit to the right of your underlined numeral is less than 5, you will round your number down.
When rounding up, add 1 to your underlined numeral and then change all of the digits to the right of the underlined numeral to zeros.
When rounding down, the underlined numeral stays the same and all of the digits to the right of it change to zeros.
103,467 = 103,500
b. 1,785,302 ________________
Answer: 2,000,000
Look at the digit to the right of your underlined numeral. Determine if it is greater than or equal to 5. If so, you will round your underlined digit up. If the digit to the right of your underlined numeral is less than 5, you will round your number down.
When rounding up, add 1 to your underlined numeral and then change all of the digits to the right of the underlined numeral to zeros.
When rounding down, the underlined numeral stays the same and all of the digits to the right of it change to zeros.
1,785,302 = 2,000,000
Question 14.
a. 23,456 _____________
Answer: 23,000
Look at the digit to the right of your underlined numeral. Determine if it is greater than or equal to 5. If so, you will round your underlined digit up. If the digit to the right of your underlined numeral is less than 5, you will round your number down.
When rounding up, add 1 to your underlined numeral and then change all of the digits to the right of the underlined numeral to zeros.
When rounding down, the underlined numeral stays the same and all of the digits to the right of it change to zeros.
23,456 = 23,000
b. 103,728 _____________
Answer: 103,700
Look at the digit to the right of your underlined numeral. Determine if it is greater than or equal to 5. If so, you will round your underlined digit up. If the digit to the right of your underlined numeral is less than 5, you will round your number down.
When rounding up, add 1 to your underlined numeral and then change all of the digits to the right of the underlined numeral to zeros.
When rounding down, the underlined numeral stays the same and all of the digits to the right of it change to zeros.
103,728 = 103,700
Place the numbers in order from least to greatest.
Question 15.
1.5, 1.7, \(\frac{1}{150}\), \(\frac{8}{3}\) _______________
Answer: \(\frac{1}{150}\), 1.5, 1.7, \(\frac{8}{3}\)
\(\frac{1}{150}\) = 0.00667
\(\frac{8}{3}\) = 2.667
Placing the numbers in order from least to greatest:
0.00667, 1.5, 1.7, 2.667
\(\frac{1}{150}\), 1.5, 1.7, \(\frac{8}{3}\)
Question 16.
0.85, 0.75, \(\frac{5}{6}\), \(\frac{2}{3}\) _______________
Answer: \(\frac{2}{3}\), 0.75, \(\frac{5}{6}\), 0.85
\(\frac{5}{6}\) = 0.833
\(\frac{2}{3}\) = 0.666
0.666, 0.75, 0.833, 0.85
\(\frac{2}{3}\), 0.75, \(\frac{5}{6}\), 0.85
Convert improper fractions into mixed numbers. Convert mixed numbers into improper fractions.
Question 17.
a. \(\frac{29}{12}\) = _______________
Answer: 2\(\frac{5}{12}\)
\(\frac{29}{12}\)
Divide the number, quotient and reminder should be mentioned in mixed number
= 2\(\frac{5}{12}\)
b. \(\frac{23}{5}\) = ________________
Answer: 4\(\frac{3}{5}\)
\(\frac{23}{5}\)
Divide the number, quotient and reminder should be mentioned in mixed number
= 4\(\frac{3}{5}\)
c. \(\frac{10}{4}\) = _________________
Answer: 2\(\frac{2}{4}\)
\(\frac{10}{4}\)
Divide the number, quotient and reminder should be mentioned in mixed number
= 2\(\frac{2}{4}\)
Question 18.
a. 4\(\frac{1}{2}\) = _______________
Answer: \(\frac{9}{2}\)
4\(\frac{1}{2}\)
multiply the mixed numbers and add them.
= \(\frac{9}{2}\)
b. 7\(\frac{2}{7}\) = _______________
Answer: \(\frac{51}{7}\)
7\(\frac{2}{7}\)
multiply the mixed numbers and add them.
= \(\frac{51}{7}\)
c. 8\(\frac{1}{8}\) = ________________
Answer: \(\frac{65}{8}\)
8\(\frac{1}{8}\)
multiply the mixed numbers and add them.
= \(\frac{65}{8}\)
Calculate how much time has elapsed in each problem.
Question 19.
Answer:
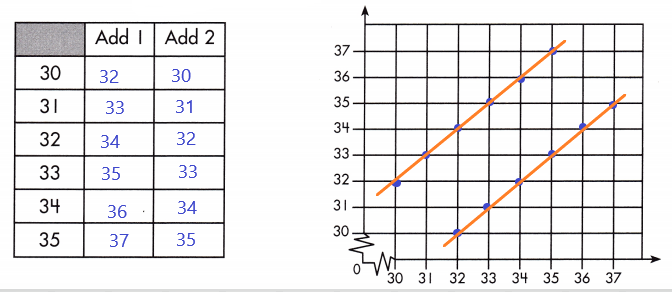
The given numbers are coordinates of X-axis. Take any two numbers as Y coordinates for each X coordinate. Then Plot the two sets of numbers in the graph.
Evaluate each expression below.
Question 20.
a. 21 ÷ 3 + (3 × 9) × 9 + 5 = ______________
Answer: 255
According to BODMAS rule, the brackets have to be solved first followed by powers or roots (i.e. of), then Division, Multiplication, Addition, and at the end Subtraction.
21 ÷ 3 + (3 × 9) × 9 + 5
= 21 ÷ 3 + 27 × 9 + 5
= 7 + 27 × 9 + 5
= 7 + 243 +5
= 255
b. 18 ÷ 6 × (4 – 3) + 6 = _____________
Answer: 9
According to BODMAS rule, the brackets have to be solved first followed by powers or roots (i.e. of), then Division, Multiplication, Addition, and at the end Subtraction.
18 ÷ 6 × (4 – 3) + 6
= 18 ÷ 6 × 1 + 6
= 3 × 1 + 6
= 3 + 6
= 9
Question 21.
a. 14 – 8 + 3 + 8 × (24 ÷ 8) = _____________
Answer: -21
According to BODMAS rule, the brackets have to be solved first followed by powers or roots (i.e. of), then Division, Multiplication, Addition, and at the end Subtraction.
14 – 8 + 3 + 8 × (24 ÷ 8)
= 14 – 8 + 3 + 8 × 3
= 14 – 8 + 3 + 24
= 14 – 35
= -21
b. 4 × 5 + (14 + – 36 ÷ 98) = _____________
Answer: 33.64
According to BODMAS rule, the brackets have to be solved first followed by powers or roots (i.e. of), then Division, Multiplication, Addition, and at the end Subtraction.
4 × 5 + (14 + – 36 ÷ 98)
= 4 × 5 + (14 + – 0.36)
= 4 × 5 + 13.64
= 20 + 13.64
= 33.64
Find the area and perimeter of each figure.
Question 22.
a.
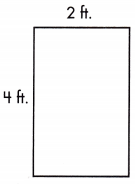
A = ___________ sq. ft.
P = ___________ ft.
Answer: A = 8 sq. ft.
P = 12 ft.
The above figure represents the rectangle
length, l = 4
breadth, b = 2
Area, A = l×b = 4 × 2 = 8 sq. ft.
Perimeter, P = 2 (l+b) = 2(4+2) = 2(6) = 12 ft.
therefore, A = 8 sq. ft.
P = 12 ft.
b.
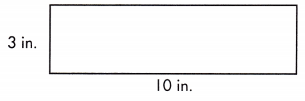
A = ___________ sq. in.
P = ___________ in.
Answer: A = 30 sq. in.
P = 26 in.
The above figure represents the rectangle
length, l = 10
breadth, b = 3
Area, A = l×b = 10 × 3 = 30 sq. in.
Perimeter, P = 2 (l+b) = 2( 10+3) = 2(13) = 26 in.
therefore, A = 30 sq. in.
P = 26 in.
c.
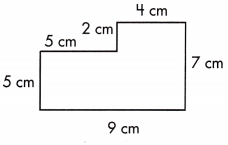
A = ___________ sq. cm.
P = ___________ cm.
Answer: A = 53 sq.cm.
P = 32 cm.
To find the area of above figure, divide the above figure into two rectangles.
Area, A = area of rectangle with 9cm and 5cm + area of rectangle with 4cm and 2cm
= 9 × 5 + 4 × 2
= 45 + 8
= 53 sq.cm.
To find the perimeter of above figure, add the dimensions of the figure
Perimeter, P = 4 + 7 + 9+ 5+ 5 +2
P = 32 cm.
Therefore, A = 53 sq.cm.
P = 32 cm.
Calculate how much time has elapsed in each problem.
Question 23.
a. Departure: 5:35 a.m. Arrival: 8:17 p.m.
___________ hours ____________ minutes
Answer: 14 hours 42 minutes
Departure: 5:35 a.m. Arrival: 8:17 p.m.
Time difference between 5:35 a.m to 12:00 noon is 6 hours 25 minutes
Time difference between 12:00 noon to 8:17 p.m is 8 hours 17 minutes
Total time elapsed = 14 hours 42 minutes
b. Departure: 9:45 p.m. Arrival: 4:56 a.m.
___________ hours ____________ minutes
Answer: 7 hours 11 minutes
Departure: 9:45 p.m. Arrival: 4:56 a.m.
Time difference between 9:45 p.m to 12:00 a.m is 2 hours 15 minutes
Time difference between 12:00 a.m to 4.56 a.m is 4 hours 56 minutes
Total time elapsed = 7 hours 11 minutes
Find the volume of each rectangular prism.
Question 24.
a.
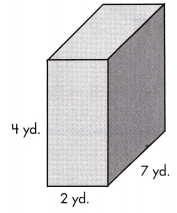
V = ____________ cu. yd.
Answer: V = 56 cu.yd.
The given dimensions from the above figure are 4 yd., 2yd., 7yd.
The volume of the above figure can be calculated by multiplying the dimensions
Volume, V = 4 × 2 × 7
V = 56 cu.yd.
b.
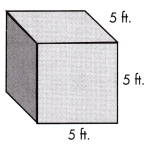
V = _____________ cu. ft.
Answer: V = 125 cu. ft.
The given dimensions from the above figure are 5 ft., 5 ft., 5 ft.
The volume of the above figure can be calculated by multiplying the dimensions
Volume, V = 5 × 5 × 5
V = 125 cu. ft.
c.
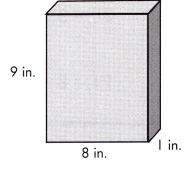
V = _____________ cu. in.
Answer: V = 72 cu. in.
The given dimensions from the above figure are 9 in., 8 in., 1 in.
The volume of the above figure can be calculated by multiplying the dimensions
Volume, V = 9 × 8 × 1
V = 72 cu. in.
Question 25.
Circle all the rectangles.
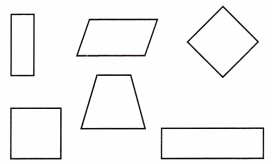
Answer:

A rectangle is a type of quadrilateral with four right angles and opposites sides are parallel to each other.
A square is a special kind of rectangle, it is one where all the sides have the same length. Thus every square is a rectangle because it is a quadrilateral with all four angles right angles. However not every rectangle is a square, to be a square its sides must have the same length.
Question 26.
Fill in the blanks to complete the hierarchy diagram.
Answer:
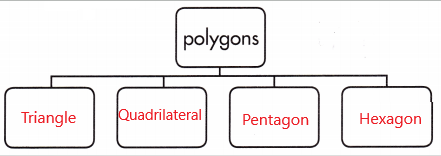
Polygon – A closed plane figure formed from line segments that meet only at their endpoints.
Traingle – A three sided polygon.
Pentagon – A five sided polygon.
Hexagon – A six sided polygon.
Quadrilateral – A four sided polygon.
Refer to the grid to the right. Name the point for each ordered pair.
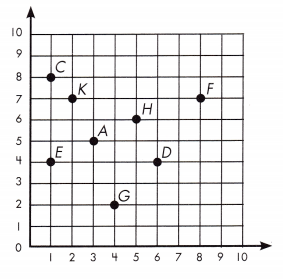
Question 27.
a. (6, 4) _____________
Answer: D
The position of any point of a grid can be described by an ordered pair of numbers. The two numbers are named in order: (x, y). Point D on the grid at the right is named by the ordered pair (6,4). It is located at 6 on the horizontal scale (x) and at 4 on the vertical scale (y). The number on the horizontal scale is always named first in an ordered pair.
b. (1, 8) ____________
Answer: C
The position of any point of a grid can be described by an ordered pair of numbers. The two numbers are named in order: (x, y). Point C on the grid at the right is named by the ordered pair (1,8). It is located at 1 on the horizontal scale (x) and at 8 on the vertical scale (y). The number on the horizontal scale is always named first in an ordered pair.
Question 28.
a. (1, 4) ___________
Answer: E
The position of any point of a grid can be described by an ordered pair of numbers. The two numbers are named in order: (x, y). Point E on the grid at the right is named by the ordered pair (1,4). It is located at 1 on the horizontal scale (x) and at 4 on the vertical scale (y). The number on the horizontal scale is always named first in an ordered pair.
b. (3, 5) _____________
Answer: A
The position of any point of a grid can be described by an ordered pair of numbers. The two numbers are named in order: (x, y). Point A on the grid at the right is named by the ordered pair (3,5). It is located at 3 on the horizontal scale (x) and at 5 on the vertical scale (y). The number on the horizontal scale is always named first in an ordered pair.
Solve.
Question 29.
India’s house is at point C. She walks to school, which is at point G. First, she walks east, and then south. How many blocks does India walk to get to school?
India walks _____________ blocks to get to school.
Answer: 9 blocks
India’s house is at point C. She walks to school, which is at point G. First, she walks east, and then south.
She walks 3 blocks to the east first. And, then she walks 6 blocks to the south.
Therefore, The total number of blocks India walks to get to school = 3 + 6 = 9 blocks