Practice with the help of Spectrum Math Grade 5 Answer Key Chapter 8 Lesson 8.3 Using Line Plots to Solve Measurement Problems regularly and improve your accuracy in solving questions.
Spectrum Math Grade 5 Chapter 8 Lesson 8.3 Using Line Plots to Solve Measurement Problems Answers Key
A line plot is used to mark how many times something occurs in a data set. Line plots can be used to organize information to solve problems.
A pitcher holds 2 quarts of iced tea. There are several glasses being filled that hold various amounts—2 glasses hold \(\frac{1}{8}\) qt., 1 glass holds \(\frac{1}{4}\) qt., and 3 glasses hold \(\frac{1}{3}\) qt. How much iced tea will be left in the pitcher?
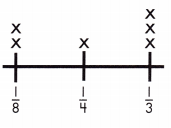
2 – [(2 × \(\frac{1}{8}\)) + (\(\frac{1}{4}\)) + (3 × \(\frac{1}{3}\))] =
2 – [(\(\frac{2}{8}\) + \(\frac{1}{4}\) + \(\frac{3}{3}\)) = 2 – (\(\frac{1}{4}\) + \(\frac{1}{4}\) + 1) =
2 – 1\(\frac{1}{2}\) = \(\frac{1}{2}\) qt.
Draw a line plot to organize the information. Then, solve the problems.
Question 1.
Andre needs to get something out of the top of a closet, but cannot reach the shelf. He needs to construct something to stand on to reach the top, which is 3 feet too tall. He has 2 phone books that are each \(\frac{1}{4}\) foot tall, 1 step stool that is \(\frac{1}{2}\) foot tall, and one chair that is 1\(\frac{1}{3}\) feet tall. Will Andre’s tower make him tall enough to reach the top?
Answer:
No, the tower will not be tall enough.
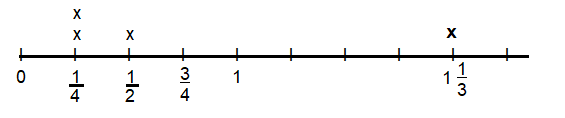
Explanation:
Andre needs to construct something to stand on to reach the top, which is 3 feet too tall.
He has 2 phone books that are each \(\frac{1}{4}\) foot tall,
1 step stool that is \(\frac{1}{2}\) foot tall,
one chair that is 1\(\frac{1}{3}\) feet tall.
3 -[(2 × \(\frac{1}{4}\)) + 1 x (\(\frac{1}{2}\)) + (1 × \(\frac{4}{3}\))]
= 3 – (\(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{4}{3}\))
= 3 – \(\frac{3 + 3 + 8}{6}\)
= 3 – \(\frac{14}{6}\)
= 3 – \(\frac{7}{3}\)
= \(\frac{9 – 7}{3}\)
= \(\frac{2}{3}\) ft.
Question 2.
Getting ready for a science experiment, Mr. Yip has put water into 8 1-pint beakers. Two beakers hold \(\frac{1}{4}\) pint, 3 beakers hold \(\frac{3}{8}\) pint, 2 beakers hold \(\frac{5}{6}\) pint, and 1 beaker holds \(\frac{5}{8}\) pint. If Mr. Yip wants to split the water equally between the 8 beakers, how much water will be in each beaker?
Answer:
3\(\frac{11}{12}\) Pint of water in each beaker.
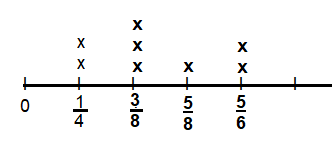
Explanation:
Mr. Yip has put water into 8 1-pint beakers.
Two beakers hold \(\frac{1}{4}\) pint,
3 beakers hold \(\frac{3}{8}\) pint,
2 beakers hold \(\frac{5}{6}\) pint,
1 beaker holds \(\frac{5}{8}\) pint.
If Mr. Yip wants to split the water equally between the 8 beakers,
the water in each beaker is,
2 x \(\frac{1}{4}\) + 3 x \(\frac{3}{8}\) + 2 x \(\frac{5}{6}\) + 1 x \(\frac{5}{8}\)
= \(\frac{2}{4}\) +\(\frac{3×3}{8}\) + \(\frac{2×5}{6}\) + \(\frac{1×5}{8}\)
= 3\(\frac{11}{12}\)