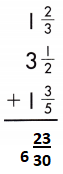Practice with the help of Spectrum Math Grade 5 Answer Key Chapter 5 Lesson 5.4 Adding Mixed Numbers regularly and improve your accuracy in solving questions.
Spectrum Math Grade 5 Chapter 5 Lesson 5.4 Adding Mixed Numbers Answers Key
Find the common denominator (8) and rename the fractions.
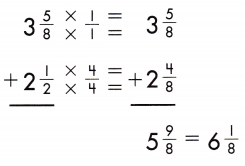
Add the fractions.
Add the whole numbers. Simplify and rename improper fractions.
Add. Write answers in simplest form.
Question 1.
a.
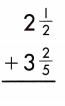
Answer:
Find the common denominator and rename the fractions.
2\(\frac{1}{2}\) + 3\(\frac{2}{5}\)
Add the fractions.
2 + \(\frac{1}{2}\) + 3 + \(\frac{2}{5}\)
Add the whole numbers. Simplify and rename improper fractions.
2 + 3 = 5
\(\frac{1}{2}\) + \(\frac{2}{5}\)
LCD is 10.
\(\frac{5}{10}\) + \(\frac{4}{10}\) = \(\frac{9}{10}\)
5 + \(\frac{9}{10}\) = 5\(\frac{9}{10}\)
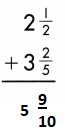
b.
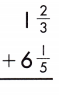
Answer:
Find the common denominator and rename the fractions.
1\(\frac{2}{3}\) + 6\(\frac{1}{5}\)
Add the fractions.
1 + \(\frac{2}{3}\) + 6 + \(\frac{1}{5}\)
Add the whole numbers. Simplify and rename improper fractions.
1 + 6 = 7
\(\frac{2}{3}\) + \(\frac{1}{5}\)
LCD is 15.
\(\frac{10}{15}\) + \(\frac{3}{15}\) = \(\frac{13}{15}\)
7 + \(\frac{13}{15}\) = 7\(\frac{13}{15}\)
c.
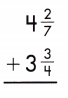
Answer:
Find the common denominator and rename the fractions.
4\(\frac{2}{7}\) + 3\(\frac{3}{4}\)
Add the fractions.
4 + \(\frac{2}{7}\) + 3 + \(\frac{3}{4}\)
Add the whole numbers. Simplify and rename improper fractions.
4 + 3 = 7
\(\frac{2}{7}\) + \(\frac{3}{4}\)
LCD is 28
\(\frac{8}{28}\) + \(\frac{21}{28}\) = \(\frac{29}{28}\) = 1\(\frac{1}{28}\)
7 + 1\(\frac{1}{28}\) = 8\(\frac{1}{28}\)
d.
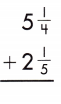
Answer:
Find the common denominator and rename the fractions.
5\(\frac{1}{4}\) + 2\(\frac{1}{5}\)
Add the fractions.
5 + \(\frac{1}{4}\) + 2 + \(\frac{1}{5}\)
Add the whole numbers. Simplify and rename improper fractions.
5 + 2 = 7
\(\frac{1}{4}\) + \(\frac{1}{5}\)
LCD is 20
\(\frac{5}{20}\) + \(\frac{4}{20}\) = \(\frac{9}{20}\)
7 + \(\frac{9}{20}\) = 7\(\frac{9}{20}\)
Question 2.
a.
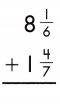
Answer:
Find the common denominator and rename the fractions.
8\(\frac{1}{6}\) + 1\(\frac{4}{7}\)
Add the fractions.
8 + \(\frac{1}{6}\) + 1 + \(\frac{4}{7}\)
Add the whole numbers. Simplify and rename improper fractions.
8 + 1 = 9
\(\frac{1}{6}\) + \(\frac{4}{7}\)
LCD is 42
\(\frac{7}{42}\) + \(\frac{24}{42}\) = \(\frac{31}{42}\)
9 + \(\frac{31}{42}\) = 9 \(\frac{31}{42}\)
b.
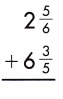
Answer:
Find the common denominator and rename the fractions.
2\(\frac{5}{6}\) + 6\(\frac{3}{5}\)
Add the fractions.
2 + \(\frac{5}{6}\) + 6 + \(\frac{3}{5}\)
Add the whole numbers. Simplify and rename improper fractions.
2 + 6 = 8
\(\frac{5}{6}\) + \(\frac{3}{5}\)
LCD is 30
\(\frac{25}{30}\) + \(\frac{18}{30}\) = \(\frac{43}{30}\) = 1\(\frac{13}{30}\)
8 + 1\(\frac{13}{30}\) = 9 \(\frac{13}{30}\)
c.
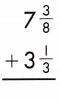
Answer:
Find the common denominator and rename the fractions.
7\(\frac{3}{8}\) + 3\(\frac{1}{3}\)
Add the fractions.
7 + \(\frac{3}{8}\) + 3 + \(\frac{1}{3}\)
Add the whole numbers. Simplify and rename improper fractions.
7 + 3 = 10
\(\frac{3}{8}\) + \(\frac{1}{3}\)
LCD is 24
\(\frac{9}{24}\) + \(\frac{8}{24}\) = \(\frac{17}{24}\)
10 + \(\frac{17}{24}\) = 10\(\frac{17}{24}\)
d.
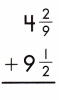
Answer:
Find the common denominator and rename the fractions.
4\(\frac{2}{9}\) + 9\(\frac{1}{2}\)
Add the fractions.
4 + \(\frac{2}{9}\) + 9 + \(\frac{1}{2}\)
Add the whole numbers. Simplify and rename improper fractions.
4 + 9 = 13
\(\frac{2}{9}\) + \(\frac{1}{2}\)
LCD is 18.
\(\frac{4}{18}\) + \(\frac{9}{18}\) = \(\frac{13}{18}\)
13 + \(\frac{13}{18}\) = 13\(\frac{13}{18}\)
Question 3.
a.
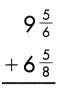
Answer:
Find the common denominator and rename the fractions.
9\(\frac{5}{6}\) + 6\(\frac{5}{8}\)
Add the fractions.
9 + \(\frac{5}{6}\) + 6 + \(\frac{5}{8}\)
Add the whole numbers. Simplify and rename improper fractions.
9 + 6 = 15
\(\frac{5}{6}\) + \(\frac{5}{8}\)
LCD is 24
\(\frac{20}{24}\) + \(\frac{15}{24}\) = \(\frac{35}{24}\) = 1\(\frac{11}{24}\)
15 + 1\(\frac{11}{24}\) = 16\(\frac{11}{24}\)
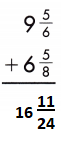
b.
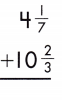
Answer:
Find the common denominator and rename the fractions.
4\(\frac{1}{7}\) + 10\(\frac{2}{3}\)
Add the fractions.
4 + \(\frac{1}{7}\) + 10 + \(\frac{2}{3}\)
Add the whole numbers. Simplify and rename improper fractions.
4 + 10 = 14
\(\frac{1}{7}\) + \(\frac{2}{3}\)
LCD is 21
\(\frac{3}{21}\) + \(\frac{14}{21}\) = \(\frac{17}{21}\)
14 + \(\frac{17}{21}\) = 14\(\frac{17}{21}\)
c.
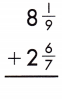
Answer:
Find the common denominator and rename the fractions.
8\(\frac{1}{9}\) + 2\(\frac{6}{7}\)
Add the fractions.
8 + \(\frac{1}{9}\) + 2 + \(\frac{6}{7}\)
Add the whole numbers. Simplify and rename improper fractions.
8 + 2 = 10
\(\frac{1}{9}\) + \(\frac{6}{7}\)
LCD is 63.
\(\frac{7}{63}\) + \(\frac{54}{63}\) = \(\frac{61}{63}\)
10 + \(\frac{61}{63}\) = 10\(\frac{61}{63}\)
d.
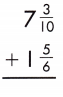
Answer:
Find the common denominator and rename the fractions.
7\(\frac{3}{10}\) + 1\(\frac{5}{6}\)
Add the fractions.
7 + \(\frac{3}{10}\) + 1 + \(\frac{5}{6}\)
Add the whole numbers. Simplify and rename improper fractions.
7 + 1 = 8
\(\frac{3}{10}\) + \(\frac{5}{6}\)
LCD is 30
\(\frac{9}{30}\) + \(\frac{25}{30}\) = \(\frac{34}{30}\) = \(\frac{17}{15}\) = 1\(\frac{2}{15}\)
8 + 1\(\frac{2}{15}\) = 9\(\frac{2}{15}\)
Add. Write answers in simplest form.
Question 1.
a.
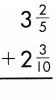
Answer:
Find the common denominator and rename the fractions.
3\(\frac{2}{5}\) + 2\(\frac{3}{10}\)
Add the fractions.
3 + \(\frac{2}{5}\) + 2 + \(\frac{3}{10}\)
Add the whole numbers. Simplify and rename improper fractions.
3 + 2 = 5
\(\frac{2}{5}\) + \(\frac{3}{10}\)
LCD is 10
\(\frac{4}{10}\) + \(\frac{3}{10}\) = \(\frac{7}{10}\)
5 + \(\frac{7}{10}\) = 5\(\frac{7}{10}\)
b.
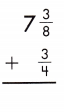
Answer:
Find the common denominator and rename the fractions.
7\(\frac{3}{8}\) + \(\frac{3}{4}\)
Add the fractions.
Add the whole numbers. Simplify and rename improper fractions.
7 + \(\frac{3}{8}\) + \(\frac{3}{4}\)
\(\frac{3}{8}\) + \(\frac{3}{4}\)
LCD is 8.
\(\frac{3}{8}\) + \(\frac{6}{8}\) = \(\frac{9}{8}\)
7 + 1\(\frac{1}{8}\) = 8\(\frac{1}{8}\)
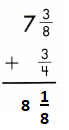
c.
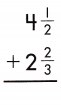
Answer:
Find the common denominator and rename the fractions.
4\(\frac{1}{2}\) + 2\(\frac{2}{3}\)
Add the fractions.
4 + \(\frac{1}{2}\) + 2 + \(\frac{2}{3}\)
Add the whole numbers. Simplify and rename improper fractions.
4 + 2 = 6
\(\frac{1}{2}\) + \(\frac{2}{3}\)
LCD is 6.
\(\frac{3}{6}\) + \(\frac{4}{6}\) = \(\frac{7}{6}\) = 1\(\frac{1}{6}\)
6 + 1\(\frac{1}{6}\) = 7\(\frac{1}{6}\)
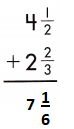
d.
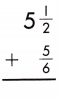
Answer:
Find the common denominator and rename the fractions.
5\(\frac{1}{2}\) + \(\frac{5}{6}\)
Add the fractions.
Add the whole numbers. Simplify and rename improper fractions.
5 + \(\frac{1}{2}\) + \(\frac{5}{6}\)
LCD is 6.
\(\frac{3}{6}\) + \(\frac{5}{6}\) = \(\frac{8}{6}\) = \(\frac{4}{3}\) = 1 \(\frac{1}{3}\)
5 + 1 + \(\frac{1}{3}\) = 6\(\frac{1}{3}\)
Question 2.
a.
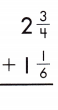
Answer:
Find the common denominator and rename the fractions.
2\(\frac{3}{4}\) + 1\(\frac{1}{6}\)
Add the fractions.
2 + \(\frac{3}{4}\) + 1 + \(\frac{1}{6}\)
Add the whole numbers. Simplify and rename improper fractions.
2 + 1 = 3
\(\frac{3}{4}\) + \(\frac{1}{6}\)
LCD is 12
\(\frac{9}{12}\) + \(\frac{2}{12}\) = \(\frac{11}{12}\)
3 + \(\frac{11}{12}\) = 3 \(\frac{11}{12}\)
b.
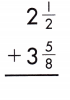
Answer:
Find the common denominator and rename the fractions.
2\(\frac{1}{2}\) + 3\(\frac{5}{8}\)
Add the fractions.
2 + \(\frac{1}{2}\) + 3 + \(\frac{5}{8}\)
Add the whole numbers. Simplify and rename improper fractions.
2 + 3 = 5
\(\frac{1}{2}\) + \(\frac{5}{8}\)
LCD is 8.
\(\frac{4}{8}\) + \(\frac{5}{8}\) = \(\frac{9}{8}\) = 1\(\frac{1}{8}\)
5 + 1 \(\frac{1}{8}\) = 6\(\frac{1}{8}\)
c.
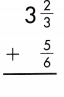
Answer:
Find the common denominator and rename the fractions.
3\(\frac{2}{3}\) + \(\frac{5}{6}\)
Add the fractions.
3 + \(\frac{2}{3}\) + \(\frac{5}{6}\)
Add the whole numbers. Simplify and rename improper fractions.
\(\frac{2}{3}\) + \(\frac{5}{6}\)
LCD is 6.
\(\frac{4}{6}\) + \(\frac{5}{6}\) = \(\frac{9}{6}\) = \(\frac{3}{2}\) = 1\(\frac{1}{2}\)
3 + 1\(\frac{1}{2}\) = 4\(\frac{1}{2}\)
d.
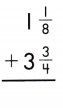
Answer:
Find the common denominator and rename the fractions.
1\(\frac{1}{8}\) + 3\(\frac{3}{4}\)
Add the fractions.
1 + \(\frac{1}{8}\) + 3 + \(\frac{3}{4}\)
Add the whole numbers. Simplify and rename improper fractions.
1 + 3 = 4
\(\frac{1}{8}\) + \(\frac{3}{4}\)
LCD is 8.
\(\frac{1}{8}\) + \(\frac{6}{8}\) = \(\frac{7}{8}\)
4 + \(\frac{7}{8}\) = 4\(\frac{7}{8}\)
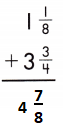
Question 3.
a.
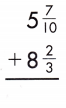
Answer:
Find the common denominator and rename the fractions.
5\(\frac{7}{10}\) + 8\(\frac{2}{3}\)
Add the fractions.
5 + \(\frac{7}{10}\) + 8 + \(\frac{2}{3}\)
Add the whole numbers. Simplify and rename improper fractions.
5 + 8 = 13
\(\frac{7}{10}\) + \(\frac{2}{3}\)
LCD is 30
\(\frac{21}{30}\) + \(\frac{20}{30}\) = \(\frac{41}{30}\) = 1\(\frac{11}{30}\)
13 + 1 + \(\frac{11}{30}\) = 14\(\frac{11}{30}\)
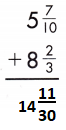
b.
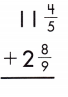
Answer:
Find the common denominator and rename the fractions.
11\(\frac{4}{5}\) + 2\(\frac{8}{9}\)
Add the fractions.
11 + \(\frac{4}{5}\) + 2 + \(\frac{8}{9}\)
Add the whole numbers. Simplify and rename improper fractions.
11 + 2 = 13
\(\frac{4}{5}\) + \(\frac{8}{9}\)
LCD is 45
\(\frac{36}{45}\) + \(\frac{40}{45}\) = \(\frac{76}{45}\) = 1\(\frac{31}{45}\)
13 + 1 + \(\frac{31}{45}\) = 14\(\frac{31}{45}\)
c.
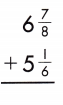
Answer:
Find the common denominator and rename the fractions.
6\(\frac{7}{8}\) + 5\(\frac{1}{6}\)
Add the fractions.
6 + \(\frac{7}{8}\) + 5 + \(\frac{1}{6}\)
Add the whole numbers. Simplify and rename improper fractions.
6 + 5 = 11
\(\frac{7}{8}\) + \(\frac{1}{6}\)
LCD is 24
\(\frac{21}{24}\) + \(\frac{4}{24}\) = \(\frac{25}{24}\) = 1\(\frac{1}{24}\)
11 + 1 + \(\frac{1}{24}\) = 12\(\frac{1}{24}\)
d.
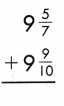
Answer:
Find the common denominator and rename the fractions.
9\(\frac{5}{7}\) + 9\(\frac{9}{10}\)
Add the fractions.
9 + \(\frac{5}{7}\) + 9 + \(\frac{9}{10}\)
Add the whole numbers. Simplify and rename improper fractions.
9 + 9 = 18
\(\frac{5}{7}\) + \(\frac{9}{10}\)
LCD is 70
\(\frac{50}{70}\) + \(\frac{63}{70}\) = \(\frac{113}{70}\) = 1 \(\frac{43}{70}\)
18 + 1 \(\frac{43}{70}\) = 19 \(\frac{43}{70}\)
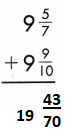
Question 4.
a.
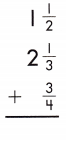
Answer:
Find the common denominator and rename the fractions.
1 \(\frac{1}{2}\) + 2 \(\frac{1}{3}\) + \(\frac{3}{4}\)
Add the fractions.
1 + \(\frac{1}{2}\) + 2 + \(\frac{1}{3}\) + \(\frac{3}{4}\)
Add the whole numbers. Simplify and rename improper fractions.
\(\frac{1}{2}\) + \(\frac{1}{3}\) + \(\frac{3}{4}\)
LCD is 12.
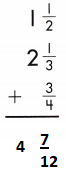
b.
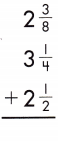
Answer:
Find the common denominator and rename the fractions.
2 \(\frac{3}{8}\) + 3 \(\frac{1}{4}\) + 2 \(\frac{1}{2}\)
Add the fractions.
2 + \(\frac{3}{8}\) + 3 + \(\frac{1}{4}\) + 2 + \(\frac{1}{2}\)
Add the whole numbers. Simplify and rename improper fractions.
2 + 3 + 2 = 7
\(\frac{3}{8}\) + \(\frac{1}{4}\) + \(\frac{1}{2}\) = 1\(\frac{1}{8}\)
7 + 1\(\frac{1}{8}\) = 8\(\frac{1}{8}\)
c.
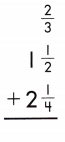
Answer:
Find the common denominator and rename the fractions.
\(\frac{2}{3}\) + 1 \(\frac{1}{2}\) + 2 \(\frac{1}{4}\)
Add the fractions.
\(\frac{2}{3}\) + 1 + \(\frac{1}{2}\) + 2 + \(\frac{1}{4}\)
Add the whole numbers. Simplify and rename improper fractions.
1 + 2 = 3
\(\frac{2}{3}\) + \(\frac{1}{2}\) + \(\frac{1}{4}\) = 1\(\frac{1}{8}\)
3 + 1\(\frac{1}{8}\) = 4\(\frac{1}{8}\)
d.
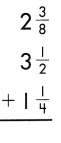
Answer:
Find the common denominator and rename the fractions.
2\(\frac{3}{8}\) + 3 \(\frac{1}{2}\) +1 \(\frac{1}{4}\)
Add the fractions.
2 + \(\frac{3}{8}\) + 3 + \(\frac{1}{2}\) +1 + \(\frac{1}{4}\)
Add the whole numbers. Simplify and rename improper fractions.
2 + 3 + 1 = 6
\(\frac{3}{8}\) + \(\frac{1}{2}\) + \(\frac{1}{4}\) = 1\(\frac{1}{8}\)
6 + 1\(\frac{1}{8}\) = 6 + 1 + \(\frac{1}{8}\) = 7 + \(\frac{1}{8}\) = 7\(\frac{1}{8}\)
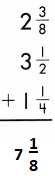
Question 5.
a.
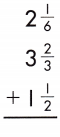
Answer:
Find the common denominator and rename the fractions.
2\(\frac{1}{6}\) + 3 \(\frac{2}{3}\) +1 \(\frac{1}{2}\)
Add the fractions.
2 + \(\frac{1}{6}\) + 3 + \(\frac{2}{3}\) +1 + \(\frac{1}{2}\)
Add the whole numbers. Simplify and rename improper fractions.
2 + 3 + 1 = 6
\(\frac{1}{6}\) + \(\frac{2}{3}\) + \(\frac{1}{2}\)
\(\frac{5}{6}\) + \(\frac{1}{2}\) = 1 \(\frac{1}{3}\)
6 + 1 \(\frac{1}{3}\) = 7\(\frac{1}{3}\)
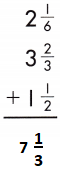
b.
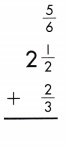
Answer:
Find the common denominator and rename the fractions.
\(\frac{5}{6}\) + 2\(\frac{1}{2}\) + \(\frac{2}{3}\)
Add the fractions.
\(\frac{5}{6}\) + 2 + \(\frac{1}{2}\) + \(\frac{2}{3}\)
Add the whole numbers. Simplify and rename improper fractions.
\(\frac{5}{6}\) + \(\frac{1}{2}\) + \(\frac{2}{3}\) = 1 \(\frac{1}{3}\)
2 + 1 \(\frac{1}{3}\) = 3 \(\frac{1}{3}\)
c.
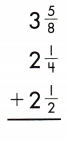
Answer:
Find the common denominator and rename the fractions.
3\(\frac{5}{8}\) + 2\(\frac{1}{4}\) +2 \(\frac{1}{2}\)
Add the fractions.
3 + \(\frac{5}{8}\) + 2 + \(\frac{1}{4}\) +2 + \(\frac{1}{2}\)
Add the whole numbers. Simplify and rename improper fractions.
3 + 2 + 2 = 7
\(\frac{5}{8}\) + \(\frac{1}{4}\) + \(\frac{1}{2}\)
\(\frac{5}{8}\) + \(\frac{3}{4}\) =1 \(\frac{3}{8}\)
7 + 1 \(\frac{3}{8}\) = 8 \(\frac{3}{8}\)
d.

Answer:
Find the common denominator and rename the fractions.
1\(\frac{2}{3\) + 3\(\frac{1}{2}\) +1 \(\frac{3}{5}\)
Add the fractions.
1 + \(\frac{2}{3\) + 3 + \(\frac{1}{2}\) +1 + \(\frac{3}{5}\)
Add the whole numbers. Simplify and rename improper fractions.
1 + 3 + 1 = 5
\(\frac{2}{3\) + \(\frac{1}{2}\) + \(\frac{3}{5}\)
1\(\frac{1}{6}\) + \(\frac{3}{5}\)
1 + \(\frac{1}{6}\) + \(\frac{3}{5}\) = 1\(\frac{23}{30}\)
5 + 1\(\frac{23}{30}\) = 6\(\frac{23}{30}\)