Practice with the help of Spectrum Math Grade 5 Answer Key Chapter 10 Lesson 10.3 Problem Solving regularly and improve your accuracy in solving questions.
Spectrum Math Grade 5 Chapter 10 Lesson 10.3 Problem Solving Answers Key
You can use coordinate grids to help you solve problems.
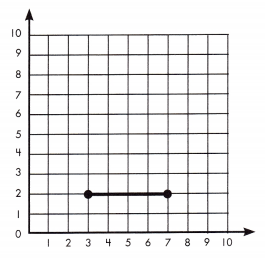
A line runs from (3, 2) to (7, 2).
How long is the line?
Count the number of points between the origin and end of the line to find the length of the line.
The distance between (3, 2) and (7, 2) is 4.
Use the coordinate grid to solve the problems.
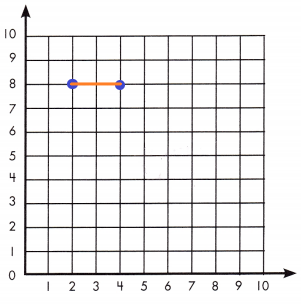
Question 1.
A line runs from (2, 8) to (4, 8). How long is the line?
Answer: 2
A line runs from (2, 8) to (4, 8).
Count the number of points between the starting point and end of the line to find the length of the line.
The distance between (2, 8) and (4, 8) is 2.
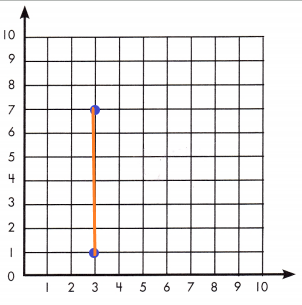
Question 2.
A line runs from (3, 1) to (3, 7). How long is the line?
Answer: 6
A line runs from (3, 1) to (3, 7)
Count the number of points between the starting point and end of the line to find the length of the line.
The distance between (3, 1) and (3, 7) is 6.
Question 3.
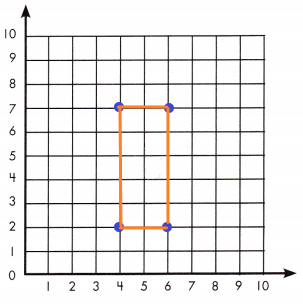
A rectangle has points at (4, 2), (6, 2), (4, 7) and (6, 7). What is the perimeter of the rectangle?
Answer: 14
A rectangle has points at (4, 2), (6, 2), (4, 7) and (6, 7)
Count the number of points between the starting point and end of the line to find the length of the line.
The distance between (4, 2) and (6, 2) is 2, which indicates length.
The distance between (4, 2) and (4,7) is 5, which indicates breadth.
Therefore, the perimeter of rectangle = 2 (l+b) = 2 (2 + 5) = 2 (7) = 14
Question 4.
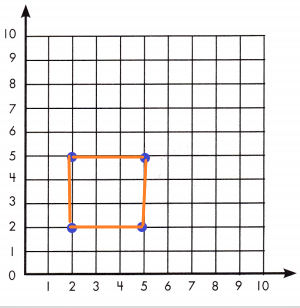
A square has points at (2, 2) and (5, 2). What is the perimeter of the square?
Answer: 12
A square has points at (2, 2) and (5, 2)
Count the number of points between the starting point and end of the line to find the length of the line.
The distance between (2, 2) and (5, 2) is 3, which indicates side of a square.
Construct the square by indicating the other sides of the square.
Therefore, perimeter of square = 4(side) = 4(3) = 12
You can use coordinate grids to help you solve problems.
Bob rides his bike 4 blocks north, 3 blocks west, and then 4 blocks south. How many blocks will Bob have to ride to get back home?
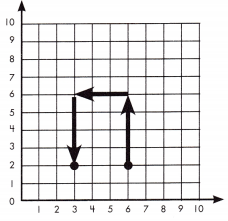
Choose a starting point for Bob (6, 2) and draw lines to show his path and solve the problem.
Bob is 3 blocks from home.
Use the coordinate grid to solve the problems.
Question 1.
Carmen’s mom drives her 8 miles north to the store. Then, they go 4 blocks west for lunch and 6 blocks south for dessert. How far will they have to drive to get back home?
They will have to drive ____________ blocks.
Answer: They will have to drive 4 blocks.
Carmen’s mom drives her 8 miles north to the store. Then, they go 4 blocks west for lunch and 6 blocks south for dessert.
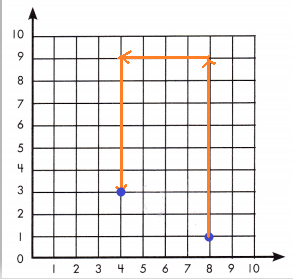
Count the number of points between the starting point and end of the line to find the distance travelled.
Therefore, they will have to drive 4 blocks.
Question 2.
On her way to school, Tisha walked 2 blocks east to her friend’s house. Then, they walked together 5 blocks north to buy snacks. Finally, they walked 3 blocks east and I block south to get to school. How far will Tisha have to walk to get home from school if she makes no stops?
Tisha will have to walk ____________ blocks.
Answer: Tisha will have to walk 5 blocks.
On her way to school, Tisha walked 2 blocks east to her friend’s house. Then, they walked together 5 blocks north to buy snacks. Finally, they walked 3 blocks east and I block south to get to school.
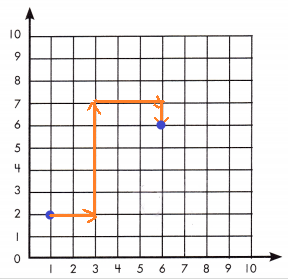
Count the number of points between the starting point and end of the line to find the distance travelled.
Tisha will have to walk 5 blocks.
Question 3.
Kenneth is at point (2, 3). He wants to go to the movies at point (8, 7). He will walk east, then north to get there. Plot Kenneth’s starting and ending points. How far will Kenneth walk to get to the movies?
Kenneth will walk ____________ blocks.
Answer: Kenneth will walk 10 blocks.
Kenneth is at point (2, 3). He wants to go to the movies at point (8, 7). He will walk east, then north to get there.
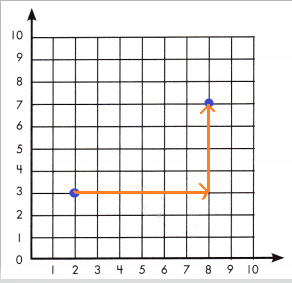
Count the number of points between the starting point and end of the line to find the distance travelled.
So, he travelled 6 blocks to east and 4 blocks to the north. Therefore, he has to walk 6 + 4, which is 10 blocks.
Kenneth will walk 10 blocks.
Question 4.
Shane and Wesley want to meet and play baseball halfway between both of their houses. Shane lives at (4, I) and Wesley lives at (10, I). Plot both boys’ houses on the grid. At which point should Shane and Wesley meet to play baseball?
They should meet at point ____________.
Answer: They should meet at point (7,1)
Shane and Wesley want to meet and play baseball halfway between both of their houses. Shane lives at (4, I) and Wesley lives at (10, I).
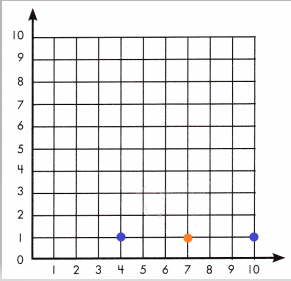
Count the number of points between the starting point and end of the line to find the distance travelled.
The total distance is 6 blocks and half of the distance is 3 points.
Therefore, They should meet at point (7,1).